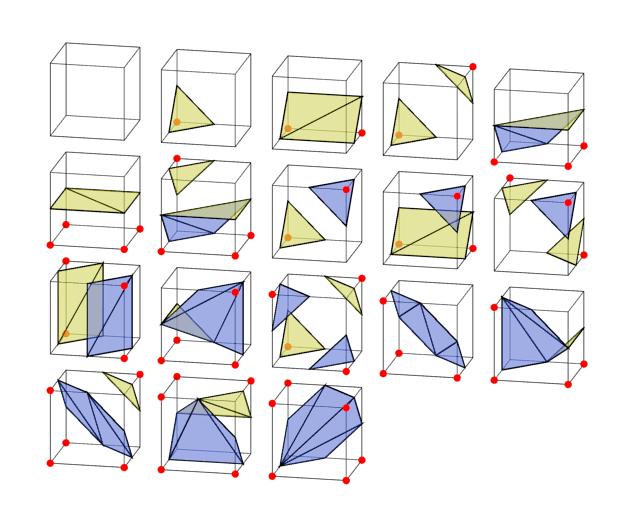
パート1.マーチングキューブの紹介

カオスからメッシュを作成する方法

Minecraftでは、エッジを明確に定義して一度に1つのブロックを削除し、任意の方向に掘ることができます。 しかし、他のゲームでは、開発者は立方体のMinecraftなしで地形をスムーズに破壊することができます。



以下は、 No Man's Sky ： video の例です。



同様の手法を使用して、MRI 、 メタボール からの画像を表示し、レリーフのボクセル化を行います。



このパートでは、破壊可能なレリーフマーチングキューブを作成する手法、およびより一般的なアプリケーション-ソリッドオブジェクトの滑らかな境界メッシュを作成する方法について説明します。 この記事では、最初に2次元のテクニック、次に3次元のテクニックを見て、第3部ではデュアルコンターリングを見ていきます。 デュアルコンターリングは、同じ効果を生み出すより高度な手法です。

私たちの目標

まず、達成したいことを決めましょう。 空間全体で離散化できる関数があり、その境界をグラフにプロットするとします。 つまり、関数が正から負へ、またはその逆への遷移を実行する場所を決定します。 破壊可能なレリーフを使用した例では、正の領域をソリッドとして、負の領域を空として解釈します。



関数は、任意の形状を記述するのに最適な方法です。 しかし、彼女はそれを描くのを助けてくれません。



レンダリングのために、例えば、関数がゼロと交差する正と負の値の間のポイントなど、その境界を知る必要があります。 マーチングキューブアルゴリズムはそのような関数を取り、その境界の多角形近似を作成し、レンダリングに使用できます。 2dでは、この境界は連続した線になります。 3Dに移動すると、メッシュになります。

2次元マーチングキューブの実装

注：このチュートリアルでは、実装方法とコードよりも概念とアイデアに重点を置いています。 実装にもっと興味がある場合は、必要なすべてのコメント付きコードを含むpython codeを調べてください。



簡単にするために、2dから始めて、3dに進みましょう。 本質的には1つのアルゴリズムであるため、2dおよび3dのアルゴリズムを「マーチングキューブ」と呼びます。

ステップ1

最初に、空間を正方形（セル）の均一なグリッドに分割します。 次に、各セルについて関数を計算することにより、セルの各頂点がソリッド領域の内側か外側かを判断できます。



円を記述する関数を以下に示し、座標が正であるすべての頂点に黒い点でマークを付けます。

ステップ2

次に、各セルを個別に処理し、対応する境界線で塗りつぶします。









単純なルックアップテーブルは、外側または内側の角度の16の可能な組み合わせを提供します。 いずれの場合も、どの境界線を描画するかを決定します。









2次元マーチングキューブのすべての組み合わせ

ステップ3

すべてのセルに対してこのプロセスを繰り返した後、各セルが独立して考慮されていても、境界が結合され、準備ができたメッシュが作成されます。









いいね！ これは一般に 、式で記述された元の円に似ていると思います。 しかし、ご覧のとおり、すべて壊れており、セグメントは45度の角度で配置されています。 これは、セルのポイントから等距離にある境界（赤い四角）の頂点を選択することにしたために発生しました。

適応性

45度の角度を取り除く最良の方法は、 適応マーチングキューブアルゴリズムです。 セルの中心点からすべての頂点境界を単純に指定する代わりに、それらをソリッドエリアに最も合うように配置できます。 これを行うには、ポイントが内側か外側かを知るだけでなく、 それがどのくらい深いかを知る必要もあります。



これは、ポイントの内側/外側の深さの尺度を提供する何らかの種類の関数が必要であることを意味します。 近似にのみ使用するため、正確である必要はありません。 半径が2.5単位の理想的な円の場合、 次の関数を使用します 。

$$

$$f（x、y）= 2.5-\ sqrt {x ^ 2 + y ^ 2}$$

正の値は内側にあり、負の値は外側にあります。



次に、数値を使用できます $$$f$ 顔のどちらかの側で、顔に沿ってどのくらいポイントが欲しいかを決定します 。









すべてをまとめると、次のようになります。









以前と同じ頂点とセグメントを持っているという事実にもかかわらず、位置のわずかな変更により、結果の図形は円のようになります。

パート2. 3次元マーチングキューブ

そのため、2Dでは、空間をグリッドに分割し、セルの各頂点について、このポイントの位置（ソリッド領域の内側または外側）を計算します。 2Dグリッドでは、各正方形には4つの角度があり、それぞれに2つのオプションがあります。つまり、各セルには $$$2 \ times 2 \ times 2 \ times 2 = 2 ^ 4 = 16$ 角度状態の可能な組み合わせ。



次に、16の各ケースのセグメントでセルを埋め、すべてのセルのすべてのセグメントが自然に結合します。 適応性を使用して、これらのセグメントをターゲットサーフェスに最適に適合させます。



良いニュースは、3次元の場合、すべてがほぼ同じように機能することです。 スペースを立方体のグリッドに分割し、それらを個別に検討し、各立方体にいくつかのエッジを描画し、それらを結合して、目的の境界メッシュを作成します。



悪いニュースは、キューブに8つの角度があることです。 $$$2 ^ {8} = 256$ 考えられるケース。 そして、これらのケースのいくつかは、2Dよりもはるかに複雑です。



非常に良いニュースは、これを理解する必要がないことです。 収集したケースをコピーして、結果のセクション（「すべてをつなぐ」）に直接進むことができます。すべての困難について考える必要はありません。 さらに強力なテクニックが必要な場合は、デュアルコンターリングについて読み始めます。

すべての困難

注：このチュートリアルでは、実装方法とコードよりも概念とアイデアに重点を置いています。 実装にもっと興味がある場合は、必要なすべてのコメント付きコードを含むpythonで3Dの実装を調べてください。



まだ読んでいますか？ 素晴らしい、私はそれが好きです。



秘密は、256種類のケースすべてを収集する必要はないということです 。 それらの多くは、鏡像または互いの回転です。









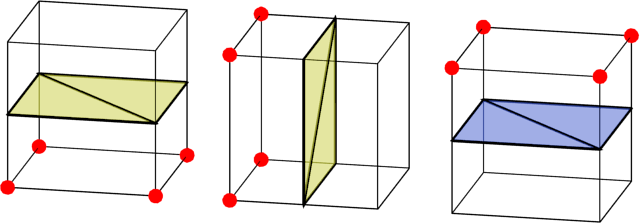
セルの3つの異なるケースを次に示します。 赤いコーナーは塗りつぶされており、他のすべては空です。 最初のケースでは、下の角は実線で、上の角は空です。したがって、境界線を正しく描画するには、セルを垂直に分割する必要があります。 便宜上、境界線の外側を黄色に、内側を青に塗りました。



残りの2つのケースは、最初のケースを回転させるだけで見つけることができます。



もう1つのトリックを使用できます。





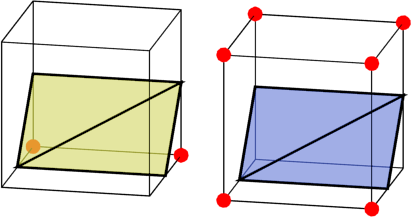
これらの2つのケースは互いに反対です。一方の立体角は他方から空であり、逆の場合も同様です。 あるケースを別のケースから簡単に生成できます-それらは同じ境界線を持ち、上下を逆にするだけです。



実際、これらすべてを考慮すると、他のすべてを生成できる18のケースのみを考慮する必要があります。

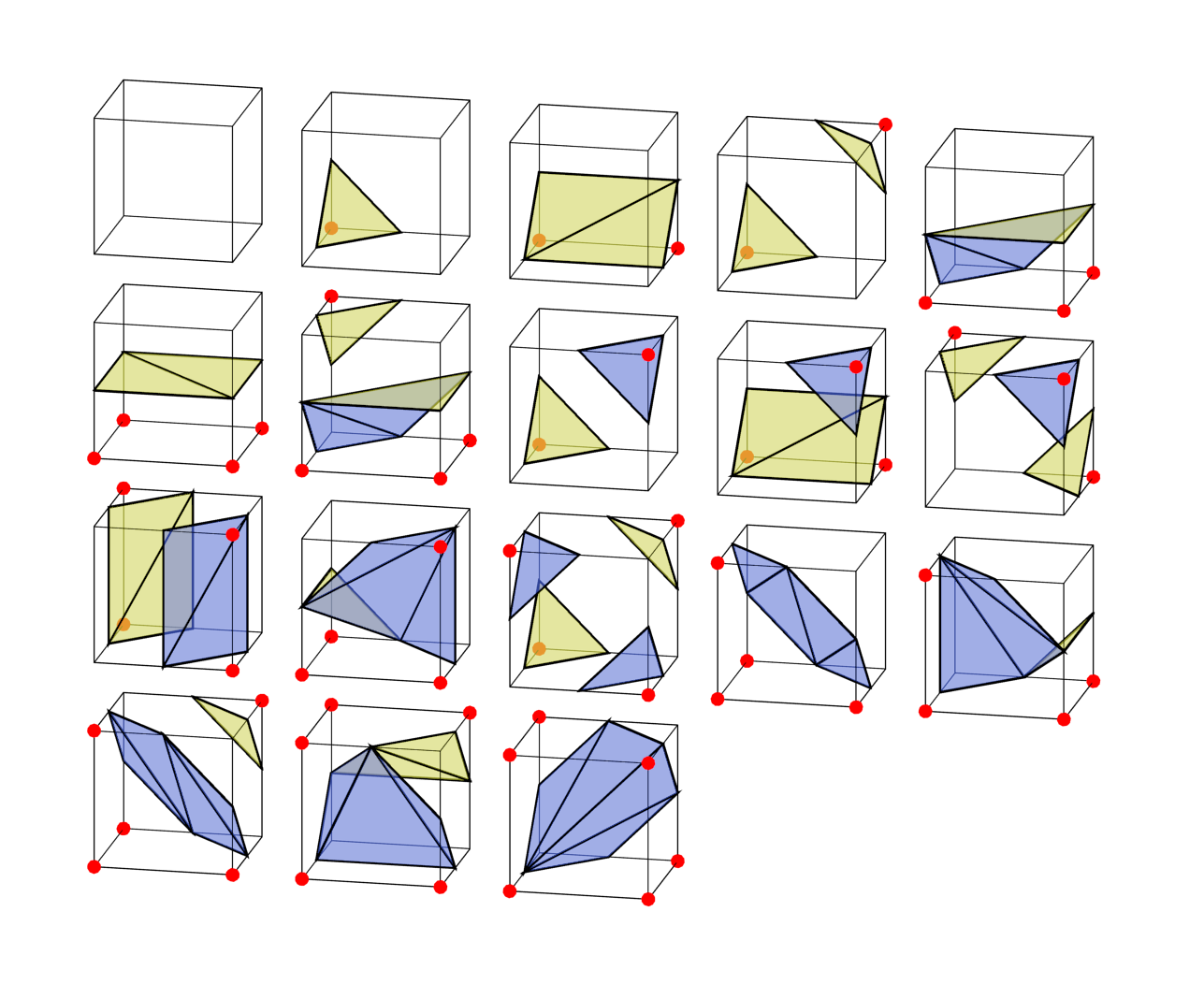
唯一の知的な人

ウィキペディアの記事やマーチングキューブのチュートリアルのほとんどを読むと、必要なケースは15件だけだと言われています。 どうして？ まあ、実際には本当です-私の回路からの3つのボトムケースは必ずしも必要ではありません。 ここでも、これらの3つのケースは、反対側の他のケースと比較して、同様の表面を与えています。









2番目と3番目の列は、空の立体角から立体角を正しく分離します。 ただし、1つのキューブを個別に検討する場合のみ。 セルの各面の端を見ると、2列目と3列目で異なることがわかります。 反転は、隣接するセルに適切に接続されず、表面に穴が残ります。 さらに3つのケースを追加すると、すべてのセルが正しく接続されます。

すべてをまとめる

2次元の場合のように、単純にすべてのセルを独立して処理できます。 これは、マーチングキューブから作成された球状メッシュです。





ご覧のとおり、球体の形状は全体として正しく行われていますが、一部の部分では、生成された狭い三角形からのカオスがあります。 この問題は、マーチングキューブよりも高度なデュアルコンターリングアルゴリズムを使用して解決できます。

パート3.二重輪郭

マーチングキューブは実装が簡単なので、よく使用されます。 しかし、アルゴリズムには多くの問題があります。

1. 複雑さ 一度に1つのキューブのみを処理する必要がありますが、多くの異なるケースを考慮する必要があるため、結果としてマーチングキューブは非常に複雑です。
   
   
   
   
   
   
   
   
   
   
2. 不確実性。 マーチングキューブのいくつかのケースは、明らかに何らかの方法で解決できません。 2Dで2つの反対の角度がある場合、それらを接続するかどうかを言うことは不可能です。
   
   
   
   
   
   
   
   
   
   
   
   3dでは、一貫性のない選択シーケンスが穴のあるメッシュを作成する可能性があるため、問題はさらに複雑になります。 2番目の部分では、この問題を解決するために追加のコードを作成する必要がありました。
3. マーチングキューブは、鋭いエッジとコーナーを作成できません。 これは、マーチングキューブを使用して近似された正方形です。
   
   
   
   
   
   
   
   
   
   
   
   角が切れました。 ここでは適応性は役に立たない-マーチングスクエアは常に、ターゲットスクエアのコーナーが表示されるセル内に直線を作成します。

どうする？

シーンにデュアルコンターリングが表示されます。

注：このチュートリアルでは、実装方法とコードよりも概念とアイデアに重点を置いています。 実装にもっと興味がある場合は、必要なすべて（ 2dおよび3d ）のコメント付きコードが含まれているpythonの実装を調べてください。



Dual Contouringはこれらの問題を解決し、はるかに拡張可能です。 その欠点は、さらに多くの情報が必要なことです $$$f（x）$ 、つまり、何が固体で空であるかを決定する関数についてです。 意味だけでなく $$$f（x）$ 勾配も $$$f '（x）$ 。 この追加情報により、マーチングキューブと比較して適応性が向上します。



デュアルコンターリングは、各セルに1つの頂点を配置し、「ドットを接続」して完全なメッシュを作成します。 マーチングキューブのように、ポイントは符号が変化する各エッジに沿って接続されます。









注：グリッド内のセルがメッシュの頂点になり、 デュアルグラフと接続されるため、名前に「デュアル」という単語が表示されます 。



マーチングキューブとは異なり、セルを個別に計算することはできません。 「ドットを接続」して完全なメッシュを見つけるには、隣接するセルを調べる必要があります。 しかし実際には、個別のケースはそれほど多くないため、これはマーチングキューブよりもはるかに単純なアルゴリズムです。 符号を変更して各エッジを見つけ、このエッジに隣接するセルの頂点を接続します。

グラデーションを取得する

半径2.5の2D円を使用した簡単な例 $$$f$ 次のように設定されます。

$$

$$f（x、y）= 2.5-\ sqrt {x ^ 2 + y ^ 2}$$

（つまり、2.5-中心点からの距離）



微分計算を使用して、勾配を計算できます。

$$

$$f '（x、y）= \ text {Vec2} \ left（\ frac {-x} {\ sqrt {x ^ 2 + y ^ 2}}、\ frac {-y} {\ sqrt {x ^ 2 + y ^ 2}} \右）$$

勾配は各ポイントの数値のペアであり、x軸またはy軸に沿って移動するときに関数がどれだけ変化するかを示します。



しかし、勾配関数を取得するために、複雑な計算は必要ありません。 変化を測定するだけです $$$f$ いつ $$$x$ そして $$$y$ 少しずれます $$$d$ 。

$$

$$f '（x、y）\約\ text {Vec2} \ left（\ frac {f（x + d、y）-f（xd、y）} {2d}、\ frac {f（x、y + d）-f（x、yd）} {2d} \右）$$

スムーズに動作します $$$f$ 選択された場合 $$$d$ かなり。 実際には、鋭いポイントを持つ関数でさえ、非常に滑らかであることがわかります。これが機能するためには、鋭いセクションの隣に勾配を計算する必要がないからです。 コードへのリンク 。

適応性

これまでのところ、マーチングキューブと同じ段階的な外観があります。 適応性を追加する必要があります。 マーチングキューブアルゴリズムでは、頂点がエッジに沿って配置される場所を選択しました。 これで、セルの内側の任意のポイントを自由に選択できます。



受け取った情報に最も近いポイント、つまり 計算値

$$

$$f（x）$$

と勾配。 コーナーではなく、エッジに沿ってグラデーションをサンプリングしたことに注意してください。









表示されたポイントを選択すると、このセルの表示面が可能な限り法線に対応することが保証されます。









実際には、セル内のすべての法線が適合するわけではありません。 最も適切なポイントを選択する必要があります。 最後のセクションでは、このポイントを選択する方法を説明します。

3Dに行く

2dと3dのケースは実際にはそれほど違いはありません。 セルは正方形ではなく立方体になりました。 エッジではなく、エッジを描画します。 しかし、違いはそこで終わります。 セル内の1つのポイントを選択する手順は同じに見えます。 そして、まだ符号の変化のあるエッジを見つけてから、隣接するセルのポイントを接続しますが、今では4つのセルがあり、4辺の多角形になります。









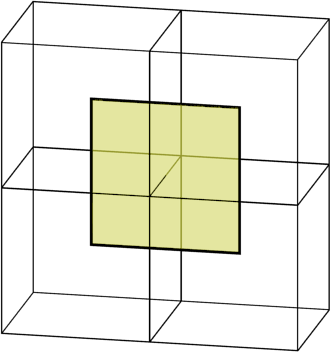
単一のエッジに関連付けられた面。 彼女はすべての隣接するセルにポイントを持っています。

結果

デュアルコンターは、マーチングキューブよりもはるかに自然な形を作成します。これは、その助けを借りて作成された球体の例で見ることができます。





3dでは、この手順は、鋭いセクションのエッジに沿ったポイントを選択し、発生する角度を選択するのに十分な信頼性があります。

頂点の位置を選択する

以前に無視した重大な問題は、法線が同じ場所を指していない場合のポイントの位置です。









3dでは、法線がより多くなるため、問題はさらに悪化します。



解決策は、すべての法線に対して相互に最適なポイントを選択することです。



まず、理想からかけ離れた場所の各法線にペナルティを割り当てます。 次に、すべてのペナルティ関数を要約します。これにより、ペナルティが楕円形になります。 その後、ペナルティが最も少ないポイントを選択します。









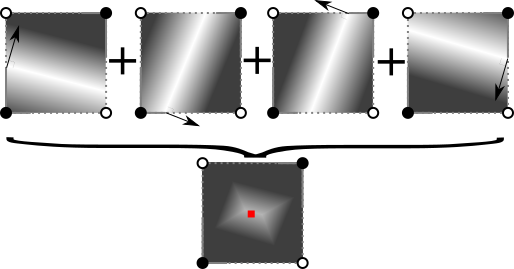
数学的な観点から見ると、個々のペナルティ関数は、現在の法線の理想的な線からの距離の2乗です。 すべての二乗項の合計は二次関数であるため、一般的なペナルティ関数はQEF （二次誤差関数）と呼ばれます。 二次関数の最小点を見つけることは、ほとんどのマトリックスライブラリで利用できる標準的な手順です。



私のpython実装では、numpyのlstsq関数を使用しました 。

問題

コリニア法線

チュートリアルのほとんどはこれに焦点を当てていますが、アルゴリズムには少し汚い秘密があります-デュアルコンターリングに関する元の記事で説明されているQEFソリューションは、実際にはうまく機能しません。



QEFを解決すると、関数の法線に最も近い点を見つけることができます。 しかし実際には、結果のポイントがセル内にあるという保証はありません 。



実際、大きな平らな表面で作業するときは、かなり外側にあることがよくあります。 この場合、この図のように、サンプリングされたすべての法線は同じか非常に近くなります。









この問題を解決するための多くのヒントを見てきました。 一部の人々はあきらめ、勾配情報を放棄し、代わりにセルの中心または境界位置の平均を使用しました。 これはSurface Netと呼ばれ、そのソリューションには少なくとも単純さがあります。



しかし、私の経験に基づいて、2つの手法を組み合わせて使用​​することをお勧めします。

テクニック1：制約付きのQEFソリューション

QEFと呼ばれる特定の関数の値を最小化するポイントを見つけることによってセルポイントを見つけたことを忘れないでください。 小さな変更を行った後、セル内に最小化ポイントを見つけることができます。

テクニック2：QEFオフセット

任意の2次関数をQEFに追加して、解決可能な別の2次関数を取得できます。 したがって、セルの中心に最小点を持つ2次関数を追加しました。



これにより、QEFソリューション全体が中心に引き寄せられます。



実際、これは法線が同一線上にある場合により大きな効果があり、ほとんどの場合結果が悪くなりますが、良いケースでは位置にはほとんど影響しません。



両方のテクニックを使用することはかなり冗長ですが、最高の視覚的結果を与えるように思えます。



両方の手法は、 コードでより詳細に示されています 。

自己交差

別の二重輪郭の問題は、自己交差する3Dサーフェスを生成できる場合があることです。 ほとんどの場合、彼らはこれに注意を払っていないので、私はこの問題を解決しませんでした。



彼女の決定について語る記事があります： 「オクトリーグリッドでの交差点のない輪郭」、JuおよびUdeshi、2006

均一性

結果の二重輪郭メッシュは常にタイトですが、表面は常に明確に定義されているとは限りません。 セルごとに1つのポイントしかないため、2つのサーフェスがセルを通過するとき、それらは共通です。 これは「均一」メッシュと呼ばれ、一部のテクスチャアルゴリズムで問題を引き起こす可能性があります。 この問題は、固体オブジェクトがセルのサイズよりも薄い場合、またはいくつかのオブジェクトが互いにほぼ接触している場合にしばしば発生します。









このような場合の処理​​は、基本的なデュアルコンターリングの機能を大幅に拡張したものです。 この機能が必要な場合は、Dual Contouringのこの実装またはこの記事を検討することをお勧めします。

アルゴリズム拡張

デュアルコンターリングメッシュの作成は比較的単純であるため、上記の標準グリッドとは異なるセルレイアウトでの作業に拡張する方がはるかに簡単です。 通常、 octreeのアルゴリズムを実行して、詳細が必要な場所で正確に異なるセルサイズを取得できます。 一般に、考え方は似ています-サンプリングされた法線を使用してセルごとにポイントで選択し、符号が変化する各エッジについて、隣接する4つのセルを見つけ、それらの頂点を面に結合します。 オクトツリーでは、再帰を使用してこれらのエッジと隣接セルを見つけることができます。 Matt Keaterには、これに関する詳細なチュートリアルがあります。



もう1つの興味深い拡張機能は、デュアルコンターリングの場合、内側/外側にあるものと、対応する法線のみを決定する必要があることです。 これには機能があると言いましたが、別のメッシュから同じ情報を抽出できます。 これにより、「ストラップ」を作成できます。 元のメッシュをクリアする頂点と面のきれいなセットを生成します。 例は、Blenderのremesh修飾子です。

追加の読書

• 隣接コード
• 元の記事-エルミートデータの二重輪郭-Tao Ju、Frank Losasso、Scott Schaefer、Joe Warren
• デュアルコンターリングは、多くの同様の手法の1つです。 SwiftCoderリストで長所と短所を使用した他のアプローチを参照してください。