リチャードハミング：第16章デジタルフィルター-3

「このコースの目標は、技術的な未来に向けて準備することです。」

こんにちは、Habr。 「You and Your Work」という素晴らしい記事（+219、2394のブックマーク、377kの読み取り）を覚えていますか？



そのため、ハミング（はい、はい、自己チェックおよび自己修正ハミングコード ）には、彼の講義に基づいて書かれた本があります。 男性がビジネスを話しているので、私たちはそれを翻訳します。



この本はITだけでなく、信じられないほどクールな人々の思考スタイルに関する本です。 「これは単なる肯定的な思考の責任ではありません。 素晴らしい仕事をする可能性を高める条件を説明しています。」



すでに18の（30の）章を翻訳しています。 そして、 私たちは紙版に取り組んでいます。

第16章デジタルフィルター-3

（翻訳のおかげで、Andrei Pakhomov、「前の章」で私の電話に答えてくれました。）誰が本の翻訳、レイアウト、出版を手伝いたいですか-個人のメールかmagisterludi2016@yandex.ruに書いてください



これで、非再帰的フィルターの体系的な合成を検討する準備が整いました。 このようなフィルターの合成方法は図16.1に示されており、6つの部分で構成されています。 左上には、理想的な場合に取得したいフィルターのスケッチがあります。 ローパスフィルター、ハイパスフィルター、バンドブロック、バンドパスフィルター、フィルタープラグ、または微分器です。 微分器を除くすべてのタイプのフィルターでは、通常、異なる周波数範囲で0または1に等しい伝達特性を取得する傾向がありますが、微分器では、伝達関数としてiωを取得する傾向があります。







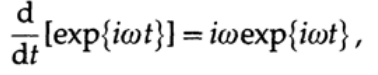
したがって、望ましい係数はiωです。



微分器の場合、特定のカットオフ周波数が設定される可能性が最も高くなります。これは、ご存じかもしれませんが、微分により信号の振幅にωを掛けることで信号振幅が増加するためです。 通常干渉が存在する高周波領域では、伝達関数の値が最も高くなります（図16.II）。 また、図15.IIにも注意してください。







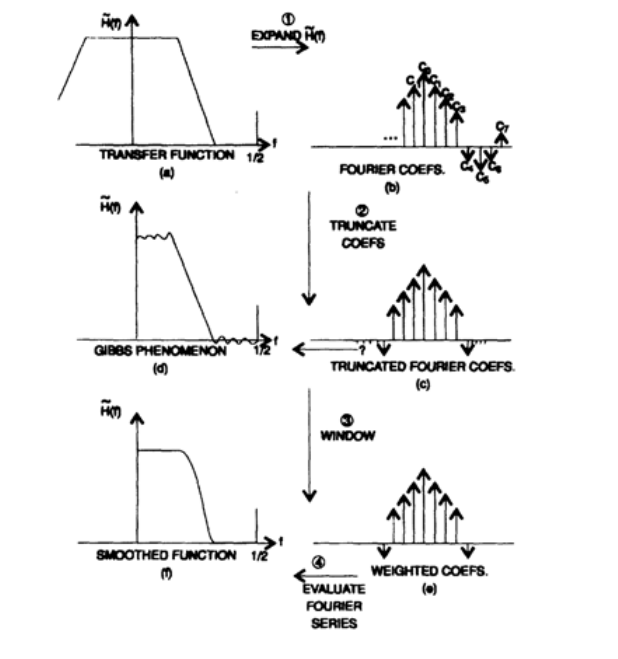
図16.I



フーリエ級数の展開の対応する項の係数は、計算式の被積分関数が単純であるため、簡単に計算されます（微分がある場合、部品による積分を使用できます）。 複素指数の形で級数展開を提示したと仮定します。 この場合、フィルター係数は、指数形式で表される系列の対応するメンバーの係数です。 図16.Iの右上隅には、係数のシンボリックグラフがあります（もちろん、係数は複素数です）。



次のステップ（下の図16.Iに示す）では、2N + 1メンバーの行の拡張を制限する必要があります（これは、長方形のウィンドウを使用するのに似ています）。 メンバーの数に対するこのような制限（図の右側）は、ギブス効果（図の左側）につながります。 ウィンドウ関数が重ね合わされた係数は、図の右下に表示され、最終フィルターは左下に表示されます。



上記の方法では、フーリエ級数のメンバー数（N）と窓関数の形状を選択する必要があります。 これらのパラメーターの最初の選択がタスクに適さない場合は、他のパラメーターを選択して再試行してください。 これは試行錯誤の方法です。



James Frederic Kaiserは、シリーズ係数の数の計算と特定のウィンドウ関数ファミリーから特定のウィンドウ関数の取得の両方を可能にする合成方法を提案しました。 この場合、2つのパラメーターを設定する必要があります。垂直軸に沿った理想フィルターからの偏差（δ）と、通過帯域と抑圧帯域間の遷移領域の幅（ΔF）を図16.IIIに示します。





図16.III



与えられた通過帯域f _pと抑制帯域f _pのバンドパスフィルターの場合、次の計算シーケンスが適用されます。







取得したNの値が大きすぎる場合は、フィルター設計を停止して確認する必要があります。そうでない場合は、次の手順に進みます。



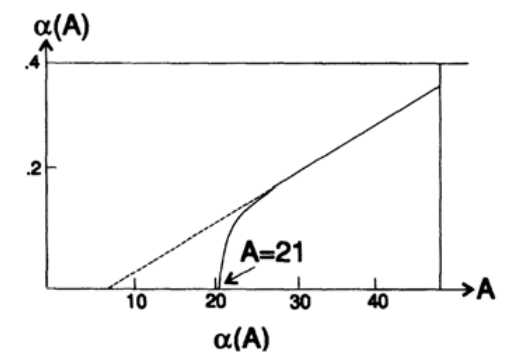
依存性α（A）は、グラフ16.IVに示されています。 初期フーリエ級数展開係数は次のように与えられます







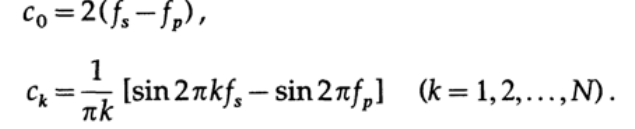
これらの係数_は、ウィンドウ関数の対応する重み係数w _kで乗算する必要があります







どこで











図表16 IV



I ₀ （ x ）は、ゼロ次の虚数引数のベッセル関数です。 その値を計算するには、平方nのおかげでシリーズが迅速に収束するため、比較的少数の項が必要です。 分母で。



I ₀ （ x ）の値を再帰的に計算するのが最善です。 与えられたxに対して、シリーズの次のメンバーは前の







ローパスまたはハイパスフィルターの場合、f _pまたはf _sの 値の1つに制限があります。 周波数バリアフィルターの場合、係数c _kの計算式はわずかに変わります。



カイザーウィンドウ関数w _kの係数を調べてみましょう。







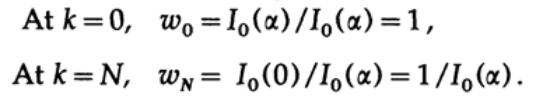
これらの数値を調べると、α> 0の場合、コサインロールオフに似ていることがわかります。







対応するウィンドウ関数は、ハンとハミングのウィンドウに似ています。 A> 21には「プラットフォーム」があります。 A <21の場合、α= 0のとき、すべての重みw _kは1に等しくなり、Lanczosウィンドウに似たウィンドウが表示されます。 Aを増やすと、プラットフォームが徐々に発生します。 したがって、Kaiserウィンドウには多くの一般的なウィンドウと同じプロパティがありますが、使用する特定のウィンドウは、偏見や当て推量ではなく、指定されたパラメーターに基づいて構築されます。



カイザーはどのようにしてこれらの式を導き出しましたか？ ある程度、試行錯誤。 最初に、彼は1つのギャップがあることを提案し、エッジ持続時間ΔFを同時に見るためにコンピューターで多くのオプションをシミュレートしました（ 信号フロントは状態0（低レベル）から1（高レベル）への信号の遷移です。この場合、通過帯域と減衰帯域との間の遷移帯域幅を参照してください。 ）およびリンギング値δ。 かなりの量の思考、ミューズのタッチ、Aの関数として定義されたものは何もない後、Aの増加に伴い、ランチョスウィンドウ（A <21）から高さ1 / I ₀ （α）のプラットフォームに到達することがわかります。 理想的なケースでは、彼は細長い回転楕円体関数を取得したかったのですが、得た値がI ₀ （ x ）で正確に近似されていることに気付きました。 彼はグラフと近似関数を作成しました。 私は彼にどのようにして指数を0.4にしたのか尋ねました。 彼は、最初は0.5で試したが、多すぎることが判明したため、次の論理的な選択になった値0.4も完璧に機能したと言いました。 これは、実験ツールとしてのコンピューターと組み合わせた既知の知識の使用が、理論研究においても非常に有用な結果につながるという事実の良い例です。

複数のスライスが存在する場合（実際には、スライスが対称的に負の周波数範囲で表示される）、Kaiserメソッドが失敗する場合があり、異なるセクションに起因する呼び出し音が重なり、呼び出し音の設定された制限値を超えます。 時々起こるこのような状況では、それほど厳しくない制限で合成を繰り返す必要があります。 プログラム全体は、最新のPCはもちろんのこと、TI-59など、手に収まる小さなプログラム可能な計算機で実行できます。



最後のフーリエ級数に戻りましょう。 フーリエ関数は、連続した間隔だけでなく、互いに等間隔の個々の点のセットでも直交するという点で注目に値します。 その結果、一連の展開では元の配列の点と同じ数の項が存在できることを除いて、理論全体は同じままです。 2Nポイントの場合、一般的な場合、最高周波数の行展開には、コサイン（サンプリングポイントでサイン値がゼロになるため）が1つしかありません。 係数は、データ値の合計に対応するフーリエ関数を掛けたものとして定義されます。 結果の表現は、丸めを考慮して、元のデータを再現します。



分解計算は、ソースデータの2N値のそれぞれに対する加算と乗算の2N演算、つまり（2N） ²加算と乗算の演算のように見えます。 2つの最適化の使用：（1）乗算演算を実行する前に同じ係数でメンバーを加算および減算し、（2）低い周波数を乗算して高い周波数を計算すると、N logN演算を必要とする高速フーリエ変換（FFT）が出現しました。 必要な計算能力のこのような削減は、科学技術の分野全体を大きく変えました。これは、以前は高コストと長い計算時間のために不可能であったものが普及しました。



そして今が人生の別の物語の時です。 FFTとCooley-Tukeyの出版物について聞いたことがあるでしょう。 FFTは、Cooley-Tukey変換またはアルゴリズムと呼ばれることもあります。 Tukeyは、FFTの基本的なアイデアの一部を教えてくれました。 当時、私は外部パンチカードでプログラムされたIBM Card Programmed Calculatorを持っていましたが、彼が念頭に置いていたバタフライ操作は、私が持っている機器では絶対に実用的ではありませんでした。 数年後、私は内部でプログラム可能なIBM-650を手に入れました。彼は再びこれらの最適化を思い出させました。 私が当時覚えていたのは、それがテューキーの数少ない悪いアイデアの一つであったということだけでした。 なぜそれが悪かったのかは絶対に忘れていました-当時持っていた機器の限界のためだけです。 したがって、FFTを実装しませんでしたが、そのときにすでに出版していた本は、このために必要なすべてをすでに知っていることを示しており、FFTを実装するのは非常に簡単でした！



道徳：何かができないということを覚えているなら、それができない主な理由も覚えておいてください。そうすれば、後で状況が変わっても、「これはできません」とは言わないでしょう。 私の間違いを考えてください！ 愚かなものはありますか？ 私のエゴにとって幸いなことに、これはよくある間違いです（そして、私はそれを複数回犯しました）が、BFTでトラブルに巻き込まれたという事実のために、私は今非常に敏感です。 また、他の人が同じようにミスを犯すことが多いことにも気づきました。 私がどれほど愚かだったのか、このために逃したどのような機会の話を思い出してください、そしてそのような間違いを自分でしないでください。 何かが不可能であると判断した場合、将来不可能であると言ったときになぜ正しかったのかを詳細に学ぶ前に、再び不可能であると言わないでください。



ここで、実数領域の特定の周波数の2つの係数の二乗和または複素数領域の二乗モジュールに等しい、パワースペクトルのデリケートなトピックに戻る必要があります。 この問題を調査すると、基準値の位置に依存する係数の値とは対照的に、この値は信号自体にのみ依存し、基準点の位置には依存しないことがわかります。 スペクトルは、科学技術において非常に重要な役割を果たしています。 原子構造のブラックボックスを開き、ボーアが内部を見ることができるのは、これらのスペクトル線でした。 1925年に登場した新しい量子力学は、少なくとも何かに少し自信を持つためにすべてを変えましたが、それでもスペクトルが鍵でした。 また、内部構造を理解するために、入力信号と出力信号のスペクトル間の関係を調べることにより、ブラックボックスを定期的に調べます-それは常に一意であることに注意してくださいが、一般に、新しい理論を形成するのに十分な情報を得ます。



私たちが何をするのか、これが何を意味するのかを注意深く分析してみましょう。 通常、少なくとも私たちの想像では、アナログ信号を扱っています。 通常は無限であり、2Lの時間間隔でサンプルを取得します。 これは、信号にLanczosウィンドウを乗算することと同じです。必要に応じて長方形のウィンドウを乗算することもできます。 これは、元の信号と、対応する関数（sin x）/ x（図16.V）の畳み込みがあることを意味します。信号が長いほど、ループ（sinx）/ xが狭くなります。 各純粋なスペクトル線は、対応する（sinx）/ x曲線に沿って広がります。

図16.V

次に、一定の間隔でサンプリングし、高い周波数が低い周波数に重ねられます。 明らかに、これら2つの操作（離散化と時間制限信号）の順序に関係なく、同じ結果が得られます。 私が述べたように、一度、私は対応する代数変換を注意深く考えて、理論の観点から真実でなければならないことが実際に実際に真実であることを確認しました。



次に、PBFを使用します。PBFは、有限フーリエ級数の係数を取得するトリッキーで正確な方法です。 事実、有限フーリエ級数の形式で信号を表現できる場合、元の関数は周期的であり、サンプリング周期にサンプリング数を掛けたものに等しい周期長であると仮定します。 すべての非高調波周波数を強制的に高調波として受け入れます-連続スペクトルを強制的に線形スペクトルに変換します。 このようなマッピングは局所的な効果ではありません。非高調波周波数がすべての高調波周波数と隣接する周波数で最大の方法で重なり合うことは容易にわかりますが、同時に、かなり非自明な方法で、より遠い周波数にも影響を与えます。



統計領域からの標準的なトリックである平均を差し引くことは避けました。これは、利便性やキャリブレーションに使用されます。 このような手法は、スペクトルのゼロ周波数の振幅をゼロに減らし、スペクトルに深刻なギャップを生じさせます。 窓関数が続いて使用される場合、それは隣接する周波数でこのギャップを単純に広げます。 Tukeyのデータを処理するとき、飛行機またはロケットの飛行データから線形または2次のトレンドを差し引くことがよくありました。 しかし、2つの信号の合計のスペクトルは決してスペクトルの合計ではありません！ 2つの関数を組み合わせると、個々の周波数が代数的に加算され、相互に増幅し、完全に相殺することができます。これにより、完全に誤った結果になります。 係数の係数は1 / kに減少するため、トレンドラインの最後には大きなギャップがあります（関数は周期的であると仮定していることに注意してください）。 何を置き換えることができるのかわからないので、私たちはまだ部分的にそれらを使用します。



しかし、理論に戻ります。 実際のノイズの各スペクトルは、周波数が無限になる傾向があるため、かなり急速に減少します。そうしないと、エネルギーが無限になります。 しかし、サンプリングプロセス自体が高い周波数を低い周波数に強制するため、グラフ16.VIに示すように、このような帯域の減少はフラットなスペクトルにつながる傾向があります。周波数は代数的に加算されることに注意してください。 したがって、ノイズに対してフラットなスペクトルを観測する傾向があり、スペクトルがフラットである場合、このノイズをホワイトノイズと呼びます。 信号は主に低周波領域にあります。 この記述は、オーバーサンプリング（ナイキストの定理が必要とするよりも頻繁にサンプルを取得する）の使用を含むいくつかの理由で当てはまります。これにより、平均化を使用して測定誤差を減らすことができます。 したがって、典型的なスペクトルは、グラフ16.VIに示すようになります。 したがって、ノイズを除去するためにローパスフィルターが非常に一般的です。 同じ周波数の信号からノイズを分離できる線形法はありませんが、信号周波数以外のノイズはローパスフィルターで除去できます。 したがって、オーバーサンプリングを使用すると、ローパスフィルターを使用してほとんどのノイズを除去することができます。



線形システムを扱っているという暗黙の制限があることに注意してください。 フーリエ変換を使用した株式市場の分析では、データに極端なホワイトノイズが存在することが示されました。これは、取引所で価格を予測することは不可能であると解釈されました。 ただし、これは、非線形予測子の実際の使用については何も言っていません。 ここでも、基礎となる基本原理を理解することなく、数学ツールの使用による結果の広範な誤解を観察できます。 特に基本的な知識にギャップがある場合、小さな知識は危険なものです。



デジタルフィルターのトピックの紹介で、その時点では何も知らないと思っていたことを注意深く述べました。 当時、私が知らなかったのは、再帰デジタルフィルターの設計について何も知らなかったという理由だけでしたが、その時までに既に作成していたことです。常微分方程式の数値解法に適用される予測子修正子の理論を詳細に研究したときです。 補正は、ほぼ再帰的なデジタルフィルターです！



常微分方程式のシステムを数値的に統合する方法を研究したとき、デジタルフィルターの分野のステレオタイプから解放され、すぐに、デジタルフィルターの専門家が言うように、限られた入力信号が無制限の出力信号を引き起こす可能性があることに気付きました-不安定と呼ばれるものですが、統合した場合に何が得られるかは明らかです。入力の値が一定であっても、出力が直線的に増加します。実際、私が後で月への着陸軌道の問題に遭遇したとき、空気がなく抵抗がないので、方程式に明示的な一次導関数はなく、数値積分に適した式を使用してそのような解決策を使用したいと思いました二次エラーが増加しました。加速度の計算における小さな丸め誤差は修正されず、位置の二次誤差につながります。加速度の誤差により、位置計算の誤差が2次的に増加します。これは、空気抵抗がフィードバックの役割を果たし、不適切な加速度を修正し、その結果、場所のエラーを修正する地球とは異なり、問題の根本です。



したがって、今日まで、限られた入力信号での出力信号の非指数関数的な増加として理解されるデジタルフィルターの安定性の問題に関係しています。同時に、多項式の成長が許可されます。これは、古典的なアナログフィルターから継承された標準の安定性基準ではなくなりました。制限されていない場合、すべてが溶けます-いずれにしても、統合ツールとして真剣に受け止められたことはありません



これについては、次の章で詳しく説明します。この章では、統合で重要な役割を果たす再帰フィルターに焦点を当てます。



継続するには...



誰が本の翻訳、レイアウト、出版を手伝いたいのか-個人のメールまたはメールで書くmagisterludi2016@yandex.ru



ちなみに、私たちはまた別のクールな本の翻訳を開始しました- 「The Dream Machine：The History of the Computer Revolution」 ）