👿 🌜 👌 Rとmxnetを使用した深層学習。パート1.作業の基本 👨🏼‍🤝‍👨🏻 👩‍💼 🦄

こんにちは、Habr！

この記事は、Rのmxnetライブラリを使用してニューラルネットワークを準備するためのマニュアルの最初の部分です。インスピレーションの源は、オンラインブックDeep Learning-The Straight Dopeでした。この本は、Pythonでmxnetを意識的に使用するのに十分です。そこからの例は、RのGluonインターフェイスの実装の不足に合わせて再現されます。最初の部分では、ライブラリのインストールと一般的な動作原理を検討し、回帰問題を解決するための単純な線形モデルを実装します。

内容：

1. mxnetライブラリをインストールします

異なる言語および異なるデバイスに異なるバージョン（CPU / GPU）をインストールするための明確なガイドが比較的最近登場しました。この投稿では、ドライバーやCUDA / cuDNNのインストールなどの準備手順について説明しましたが、繰り返しません。ところで、Pythonの場合、ソースから何も収集することはできませんpip install mxnet --pre

だけです。 CPUコアが比較的多く、RAMが比較的少ない状況では、ソースからビルドするときにメモリが不足する可能性があります。この場合、アセンブリをシングルスレッドモードで実行する必要があります： make -j1

。

このライブラリは、Julia、Scala、そして突然Perlコードでも使用できます。また、Raspberry Pi 3の作業に対するサポートを宣言しました。

2.使用済みデータセット

2つの属性（ num_inputs

）と1つのターゲット変数（ num_outputs

）を含む10,000件のケース（ num_examples

）の人工的なデータセットを作成します。予測変数とターゲット変数間の関係の真の形式はreal_fn()

関数によって設定され、小さなガウスノイズ0.01 * rnorm(num_examples)

この関数を使用して生成された値に追加されます。

 num_inputs <- 2 num_outputs <- 1 num_examples <- 10000 real_fn <- function(x) { 2 * x[, 1] - 3.4 * x[, 2] + 4.2 } X <- matrix(rnorm(num_examples * num_inputs), ncol = num_inputs) noise <- 0.01 * rnorm(num_examples) y <- real_fn(X) + noise

3.ニューラルネットワークのトレーニングの主な機能

mx.model.FeedForward.create()

関数は、直接分布ニューラルネットワークのトレーニングを担当します。彼女が受け入れるパラメーターのリストは次のとおりです。

symbol

シンボリック記述の形式のネットワークアーキテクチャ。これは、テンソルと損失関数の次元を指定するのではなく、類似したものであるため、計算グラフではありません。アーキテクチャはgraph.viz()

関数を使用して描画できます。以下に例を示します。
X

トレーニングに使用されるデータの行列/配列または反復子。データが完全にメモリに配置される場合は配列が使用され、配置されない場合は反復子が使用されます。いくつかの既製のイテレータ（配列用、バイナリRecordIO形式の画像用、csvファイル用）および独自のイテレータがあります。
y

はターゲット変数の値です。 X

が配列の場合にのみ設定されます。そうでない場合、反復子は正しい答えを含め、トレーニングに必要なすべてを返す必要があります。
ctx

トレーニングに使用されるデバイスまたはデバイスのリスト（CPU / GPU）。 mx.cpu()

またはmx.gpu()

を使用して作成されたMXContextクラスのオブジェクト。
begin.round

学習の反復（エポック）カウンターの初期値。デフォルト値（1）の変更は、モデルを再トレーニングする場合にのみ必要です。
num.round

の数。
optimizer

-（文字列として）名前で指定されたオプティマイザーを使用します。デフォルトは、確率的勾配降下法（ "sgd"）です。オプティマイザー設定の例を以下に示します。
initializer

-モデルパラメータの初期化スキームを設定するオブジェクト。
eval.data

リスト形式list(data = R.array, label = R.array)

または検証データを含むイテレーター。
eval.metric

モデルの品質を評価するための関数。利用可能なオプションに加えて、独自の手書きを使用することもできます。
epoch.end.callback

トレーニングの各時代の後に起動される機能。
batch.end.callback

各バッチ後に起動される関数。
array.batch.size

配列形式のデータを使用する場合のバッチのサイズ。イテレータを使用すると、mbatchサイズもイテレータに設定されます。
array.layout

「auto」、「colmajor」または「rowmajor」（デフォルトは「auto」）。配列形式：マトリックスの場合、「rowmajor」はdim(X) = c(nexample, nfeatures)

意味し、「colmajor」はdim(X) = c(nexample, nfeatures)

意味します。「rowmajor」という形式は、行列に対してのみ有効です。 mx.io.arrayiter()

関数mx.io.arrayiter()

、データを「colmajor」形式に変換することmx.io.arrayiter()

明示的に要求します。行列は、行の観測値と列の符号を持つ見慣れた形式に関連して転置されます。
kvstore

文字列として設定し、複数のデバイスで学習するときの同期スキームを担当します。デフォルトは「ローカル」です。
verbose

学習プロセスで情報メッセージを出力します。デフォルトはTRUEです。
arg.params

モデルの重みを含むNDArray配列のリストを持つオプションのパラメーター。
aux.params

追加パラメーターの同様のリスト。
input.names

入力に提供される文字の名前。
output.names

出力で受け取った文字の名前。
fixed.param

トレーニング中に固定されたままのパラメーター（トレーニングされていない）。
allow.extra.params

モデルのシンボリックな記述に従って、不要な追加パラメーターを渡すことができます。 TRUEに設定した場合、 arg.params

およびaux.params

ような追加パラメーターがある場合aux.params

エラーは表示されません。

4.イテレータ

データ配列（行列）の反復子を作成します。

 batch_size <- 4 train_data <- mx.io.arrayiter(t(X), y, batch.size = batch_size, shuffle = TRUE)

この関数は、入力または属性の配列（この場合、既に述べたように、マトリックスを転置する必要があります）、ターゲット変数の値とバッチのサイズを持つ配列を取ります。また、 shuffle = TRUE

オプションを使用したshuffle = TRUE

観測も含めました。利用可能なすべてのイテレータのリストは次のようになります。

 apropos("mx.io") # [1] "mx.io.arrayiter" "mx.io.bucket.iter" # [3] "mx.io.CSVIter" "mx.io.extract" # [5] "mx.io.ImageDetRecordIter" "mx.io.ImageRecordIter" # [7] "mx.io.ImageRecordIter_v1" "mx.io.ImageRecordUInt8Iter" # [9] "mx.io.ImageRecordUInt8Iter_v1" "mx.io.LibSVMIter"

ここで、他のオプションを検討したり、独自のイテレーターを作成したりしません。

5.ネットワークアーキテクチャ

ネットワークアーキテクチャは、 mx.symbol.*

ファミリの関数への連続した呼び出しによって記述されますmx.symbol.*

各ファミリは、完全に接続された畳み込み、プーリングなど、モデルのレイヤの抽象表現をモデルに追加します。多くのレイヤーが利用可能です：

 apropos("mx.symbol") # [1] "is.mx.symbol" # [2] "mx.symbol.abs" # [3] "mx.symbol.Activation" # [4] "mx.symbol.adam_update" # [5] "mx.symbol.add_n" # ..... # [208] "mx.symbol.transpose" # [209] "mx.symbol.trunc" # [210] "mx.symbol.uniform" # [211] "mx.symbol.UpSampling" # [212] "mx.symbol.Variable" # [213] "mx.symbol.where" # [214] "mx.symbol.zeros_like"

回帰問題を解決する単純な線形モデルを作成するには、次のコードを使用します。

 data <- mx.symbol.Variable("data") fc1 <- mx.symbol.FullyConnected(data, num_hidden = 1) linreg <- mx.symbol.LinearRegressionOutput(fc1)

結果のアーキテクチャを描画しましょう：

 graph.viz(linreg)

6.初期化子

初期化子は、ニューラルネットワークのトレーニングを開始する初期値を決定します。ネットワークは非常に単純で浅いため、正規分布を持つランダムな値で重みを初期化するだけで十分です。

 initializer <- mx.init.normal(sd = 0.1)

この場合に受け入れられる唯一のパラメーターは標準偏差です。また、 mx.init.uniform()

初期化子もあります。この初期化子の唯一のパラメーターは、値が生成される範囲の境界線です。

深いネットワークでは、適切な重みの初期化が非常に重要であるため、 mx.init.Xavier()

オプションを使用します。

このスケールの初期化スキームは、2010年にJoshua BenggioとXavier Gloroによって発明されました。現在、異なる名前で普遍的に使用されています。たとえば、 glorot_normal

glorot_uniform

glorot_normal

glorot_uniform

を見つけることができます。 Pythonのライブラリには、Rバージョンでは使用できない他の多くのイニシャライザーも含まれています。たとえば、ReLUアクティベーション機能でニューロンの重みを初期化するための優先オプションであるXe初期化を使用する方法はありません。

mx.init.Xavier()

関数のパラメーター：

rnd_type

重みが生成される分布のタイプ（「均一」または「ガウス」）を指定する文字列。
factor_type

「avg」、「in」または「out」（以下を参照）。
magnitude

は、結果の重みのスケールを設定するあまり明確ではない数値パラメーターです。

rnd_type = "uniform"

およびfactor_type = "avg"

（デフォルト）の場合、重みは範囲のランダムな値で初期化されます $[-c、c]$ どこで $c = \ sqrt {\ frac {3} {0.5 \ cdot（n_ {in} + n_ {out}）}}$ 、 $n_ {in}$ -入力（つまり、前のレイヤー）のニューロン数 $n_ {out}$ 出力（つまり、次のレイヤー）のニューロンの数です。

rnd_type = "uniform"

およびfactor_type = "in

場合、 $c = \ sqrt {\ frac {3} {n_ {in}}}$ 。同様に、 rnd_type = "uniform"

およびfactor_type = "out"

を使用すると、次のようになります。 $c = \ sqrt {\ frac {3} {n_ {out}}}$ 。

rnd_type = "gaussian"

およびfactor_type = "avg"

重みは標準偏差で正規分布から抽出されます $\ sqrt {\ frac {3} {0.5 \ cdot（n_ {in} + n_ {out}）}}$ 。

7.オプティマイザー

オプティマイザーは、ネットワークの重みの更新方法を決定します。使用可能なオプションは、sgd、rmsprop、adam、adagrad、adadeltaです。一般的な関数mx.opt.create()

を使用して、必要な設定でオプティマイザーを作成できます。

 optimizer <- mx.opt.create("sgd", learning.rate = 2e-5, momentum = 0.9)

mx.opt.create()

呼び出しに渡す各オプティマイザーのパラメーターを確認するには、ヘルプを使用します。

 ?mx.opt.sgd ?mx.opt.rmsprop ?mx.opt.adam ?mx.opt.adagrad ?mx.opt.adadelta

これらの関数を通常の方法で呼び出すことはできません（ただし、アクセスは可能です： mxnet:::mx.opt.adagrad

）。

パラメーターmx.opt.sgd()

learning.rate

速度。
momentum

-瞬間;
wd

はl2正則化の係数です（大きな重みに対してペナルティが追加されます）。
rescale.grad

重みを更新する前に、取得した勾配に乗算する値。多くの場合、 1 / batch_size

と見なされます。
clip_gradient

間隔に投影することで勾配の値を制限する $[-クリップ\ _gradient、クリップ\ _gradient]$ ;
lr_scheduler

スケジューラーは学習速度を変更します。

パラメーターmx.opt.rmsprop()

learning.rate

速度。
gamma1

勾配の二乗の移動平均の減衰係数;
gamma2

モーメント;
wd

はl2正則化の係数です（大きな重みに対してペナルティが追加されます）。
rescale.grad

重みを更新する前に、取得した勾配に乗算する値。多くの場合、 1 / batch_size

と見なされます。
clip_gradient

間隔に投影することで勾配の値を制限する $[-クリップ\ _gradient、クリップ\ _gradient]$ ;
lr_scheduler

スケジューラーは学習速度を変更します。

パラメーターmx.opt.adadelta()

：

rho

二乗勾配および二乗パラメーター更新の減衰係数。
epsilon

は、0による除算を避けるための小さな定数（1e-05）です。
wd

はl2正則化の係数です（大きな重みに対してペナルティが追加されます）。
rescale.grad

重みを更新する前に、取得した勾配に乗算する値。多くの場合、 1 / batch_size

と見なされます。
clip_gradient

間隔に投影することで勾配の値を制限する $[-クリップ\ _gradient、クリップ\ _gradient]$ 。

注意：パラメータは学習速度のために提供されていません。

AdadeltaオプティマイザーはRMSpropに似ていますが、Adadeltaは単位を変更して更新履歴を保存することで2回目の修正を行い、RMSpropは単純に2乗勾配の平均のルートを使用します。次のアルゴリズムであるAdagradは、平均およびrms勾配の平滑化バージョンを使用します。このすべての詳細については、 Deep Learningの本を参照してください。本全体を読むことをお勧めします。

パラメーターmx.opt.adagrad()

：

learning.rate

速度。
epsilon

は、0による除算を避けるための小さな定数（1e-08）です。
wd

はl2正則化の係数です（大きな重みに対してペナルティが追加されます）。
rescale.grad

重みを更新する前に、取得した勾配に乗算する値。多くの場合、 1 / batch_size

と見なされます。
clip_gradient

間隔に投影することで勾配の値を制限する $[-クリップ\ _gradient、クリップ\ _gradient]$ ;
lr_scheduler

スケジューラーは学習速度を変更します。

パラメーターmx.opt.adam()

：

learning.rate

速度。
beta1

モーメントの最初の推定の減衰係数。
beta2

—二次モーメント推定の減衰係数。
epsilon

は、0による除算を避けるための小さな定数（1e-08）です。
wd

はl2正則化の係数です（大きな重みに対してペナルティが追加されます）。
rescale.grad

重みを更新する前に、取得した勾配に乗算する値。多くの場合、 1 / batch_size

と見なされます。
clip_gradient

間隔に投影することで勾配の値を制限する $[-クリップ\ _gradient、クリップ\ _gradient]$ ;
lr_scheduler

スケジューラーは学習速度を変更します。

8.コールバック関数（コールバック）

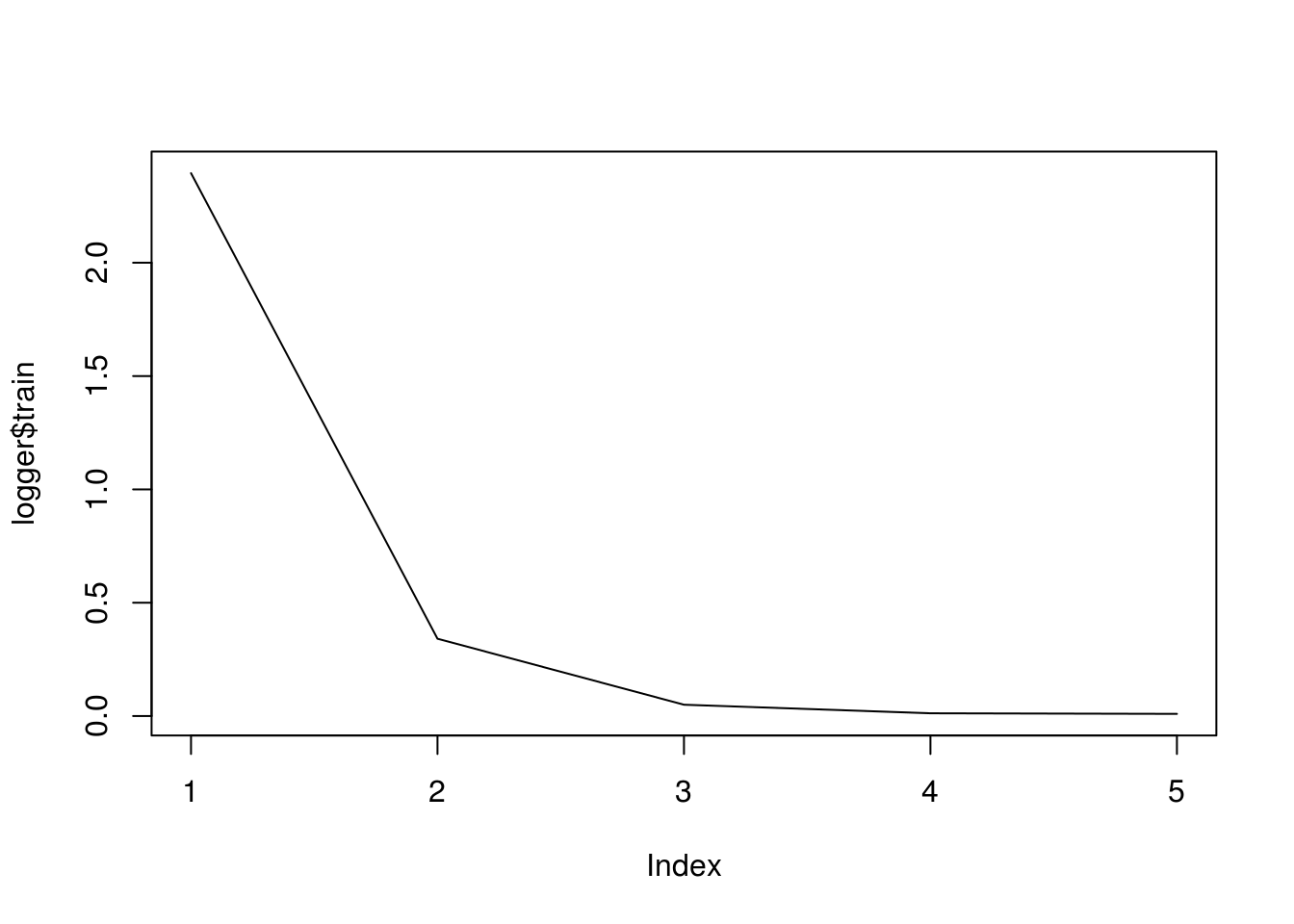
適切なコールバック関数を使用して学習履歴を保存します。

 logger <- mx.metric.logger() epoch.end.callback <- mx.callback.log.train.metric( period = 1, #  ,     logger = logger)

トレーニング後、 logger

オブジェクトにはフォームの情報が含まれます

 logger$train # [1] 2.322148818 0.318418684 0.044898842 0.011428233 0.009461375

その他のコールバック： mx.callback.early.stop()

は早期停止を担当し、 mx.callback.log.speedometer()

は指定された周波数で処理速度を表示し、 mx.callback.save.checkpoint()

は指定された間隔でモデルをファイルに保存します指定されたプレフィックス。

9.モデルトレーニング

上記の関数mx.model.FeedForward.create()

呼び出すことにより、トレーニングが開始されます。

 model <- mx.model.FeedForward.create( symbol = linreg, X = train_data, ctx = mx.cpu(), num.round = 5, initializer = initializer, optimizer = optimizer, eval.metric = mx.metric.rmse, epoch.end.callback = epoch.end.callback) ## Start training with 1 devices ## [1] Train-rmse=2.39517188021255 ## [2] Train-rmse=0.34100598193831 ## [3] Train-rmse=0.0498822148288494 ## [4] Train-rmse=0.0120600163293274 ## [5] Train-rmse=0.00946668211065784

学習の歴史を描きましょう：

 plot(logger$train, type = "l")

モデルの動作を確認しましょう：

 predict(model, t(X[1:5, ])) y[1:5] ## Warning in mx.model.select.layout.predict(X, model): Auto detect layout input matrix, use colmajor.. ## [,1] [,2] [,3] [,4] [,5] ## [1,] 0.3129134 4.070303 4.975691 8.280487 8.931004 y[1:5] ## [1] 0.3211988 4.0561930 4.9810253 8.2959409 8.9414367

すべてが機能しているので、さらに深刻な例に進むことができます！

10.実際のデータの回帰問題を解決する

この物質の既知の特性に基づいて、細胞の単層を通る物質の透過度（実際には、受動拡散の速度）を予測する例を使用して、回帰問題の解決策を考えてみましょう（詳細はこちらを参照）。

なぜそれが必要ですか

ジェネリック医薬品を登録するための特別な手順、いわゆるバイオウェーブがあります。比較薬物動態/薬力学/臨床試験（ in vivo ）の代わりに溶解度および透過性試験（ in vitro ）を実施することにより生物学的同等性を評価することが含まれます。 Caco2細胞の単層は、物質の透過性を評価するための標準モデルとして使用されます。透過性の程度を事前に予測することを学べば、実験中にテストされた候補物質の選択により意識的に近づくことができます。

説明されているタスクは、創薬におけるADME評価の作業に専念しています。 5. Caco-2透過と単純な分子特性との相関。さまざまな構造を持つ77の物質の特性と、これらの物質の透過性に関する実験データを含む表が含まれています。異なる実験中に同じ物質について得られたデータは大きく異なる可能性があることに注意してください。しかし、この問題の側面については掘り下げることはせず、出版物の著者が協力したデータを単に取り上げます。

便利なdump()

関数によって作成されたコードを使用してデータをロードします。

データの読み込み

 # df <- read_excel("caco2.xlsx") # dump("df", stdout()) df <- structure(list(name = c("acebutolol", "acebutolol_ester", "acetylsalic_acid", "acyclovir", "alprenolol", "alprenolol ester", "aminopyrin", "artemisinin", "artesunate", "atenolol", "betazolol ester", "betazolol_", "bremazocine", "caffeine", "chloramphenicol", "chlorothiazide", "chlorpromazine", "cimetidine", "clonidine", "corticosterone", "desiprarnine", "dexamethas", "dexamethas_beta_D_glucoside", "dexamethas_beta_D_glucuronide", "diazepam", "dopamine", "doxorubici", "erythromycin", "estradiol", "felodipine", "ganciclovir", "griseofulvin", "hydrochlorothiazide", "hydrocortisone", "ibuprophen", "imipramine", "indomethacin", "labetalol", "mannitol", "meloxicam", "methanol", "methotrexate", "methylscopolamine", "metoprolol", "nadolol", "naproxen", "nevirapine", "nicotine", "olsalazine", "oxprenolol", "oxprenolol ester", "phencyclidine", "Phenytoin", "pindolol", "pirenzepine", "piroxicam", "pnu200603", "practolol", "prazocin", "progesterone", "propranolol", "propranolo_ester", "quinidine", "ranitidine", "salicylic acid", "scopolamine", "sucrose", "sulfasalazine", "telmisartan", "terbutaline", "tesosterone", "timolol", "timolol_ester", "uracil", "urea", "warfarine", "zidovudine"), log_P_eff_exp = c(-5.83, -4.61, -5.06, -6.15, -4.62, -4.47, -4.44, -4.52, -5.4, -6.44, -4.81, -4.52, -5.1, -4.41, -4.69, -6.72, -4.7, -5.89, -4.59, -4.47, -4.67, -4.75, -6.54, -6.12, -4.32, -5.03, -6.8, -5.43, -4.77, -4.64, -6.27, -4.44, -6.06, -4.66, -4.28, -4.85, -4.69, -5.03, -6.21, -4.71, -4.58, -5.92, -6.16, -4.59, -5.41, -4.83, -4.52, -4.71, -6.96, -4.68, -4.51, -4.61, -4.57, -4.78, -6.36, -4.45, -6.25, -6.05, -4.36, -4.37, -4.58, -4.48, -4.69, -6.31, -4.79, -4.93, -5.77, -6.33, -4.82, -6.38, -4.34, -4.85, -4.6, -5.37, -5.34, -4.68, -5.16), log_D = c(-0.09, 1.59, -2.25, -1.8, 1.38, 2.78, 0.63, 2.22, -0.88, -1.81, 0.28, 0.63, 1.66, 0.02, 1.14, -1.15, 1.86, -0.36, 0.78, 1.78, 1.57, 1.89, 0.58, -1.59, 2.58, -0.8, -0.16, 1.26, 2.24, 3.48, -0.87, 2.47, -0.12, 1.48, 0.68, 2.52, 1, 1.24, -2.65, 0.03, -0.7, -2.53, -1.14, 0.51, 0.68, 0.42, 1.81, 0.41, -4.5, 0.45, 1.98, 1.31, 2.26, 0.19, -0.46, -0.07, -4, -1.4, 1.88, 3.48, 1.55, 3.02, 2.04, -0.12, -1.44, 0.21, -3.34, -0.42, 2.41, -1.07, 3.11, 0.03, 1.74, -1.11, -1.64, 0.64, -0.58), rgyr = c(4.64, 5.12, 3.41, 3.37, 3.68, 3.84, 2.97, 2.75, 4.02, 4.58, 5.41, 5.64, 3.43, 2.47, 3.75, 3.11, 3.74, 4.26, 2.79, 3.68, 3.4, 3.6, 5.67, 5.75, 3.28, 2.67, 4.85, 4.99, 3.44, 3.39, 3.7, 3.37, 3.11, 3.72, 3.45, 3.44, 4.16, 4.61, 2.48, 3.34, 0.84, 5.33, 3.67, 4.59, 4.37, 3.38, 2.94, 2.5, 4.62, 3.63, 3.87, 2.91, 2.97, 3.71, 3.55, 3.17, 3.89, 4.02, 4.96, 3.58, 3.63, 4.13, 3.25, 5.13, 2.14, 3.63, 3.49, 5.68, 5.29, 3.15, 3.33, 4.02, 3.98, 1.84, 1.23, 3.45, 3.14), rgyr_d = c(4.51, 5.03, 3.24, 3.23, 3.69, 3.88, 2.97, 2.75, 3.62, 4.52, 5.27, 5.39, 3.38, 2.47, 3.73, 3.11, 3.69, 4.24, 2.79, 3.71, 3.42, 3.66, 5.28, 5.23, 3.28, 2.68, 4.9, 5.01, 3.44, 3.48, 3.48, 3.37, 3.11, 3.79, 3.36, 3.45, 3.16, 4.46, 2.59, 3.36, 0.84, 5.18, 3.74, 4.53, 4.1, 3.43, 2.94, 2.5, 4.37, 3.56, 3.9, 2.91, 2.97, 3.71, 3.4, 3.26, 3.79, 4.09, 4.99, 3.62, 3.53, 4.06, 3.3, 4.57, 2.14, 3.49, 3.54, 5.53, 5.01, 3.15, 3.33, 4.01, 4.13, 1.84, 1.23, 3.5, 3.13), HCPSA = c(82.88, 77.08, 79.38, 120.63, 38.92, 35.53, 20.81, 54.27, 102.05, 86.82, 43.02, 47.14, 49.56, 45.55, 113.73, 138.76, 4.6, 105.44, 30.03, 75.95, 13.8, 90.74, 163.95, 186.88, 25.93, 75.13, 186.78, 138.69, 44.34, 50.34, 139.45, 67.55, 142.85, 93.37, 39.86, 3.56, 67.13, 93.29, 127.46, 93.21, 25.64, 204.96, 51.29, 44.88, 86.73, 76.98, 36.68, 15.1, 144.08, 48.62, 49.58, 1.49, 65.63, 52.8, 59.71, 99.19, 69.89, 64.79, 86.76, 38.1, 40.42, 36.21, 43.77, 105.15, 61.71, 57.35, 187.69, 133.67, 55.48, 79.52, 42.35, 100.74, 96.25, 66.72, 82.72, 59.47, 96.33), TPSA = c(87.66, 93.73, 89.9, 114.76, 41.49, 47.56, 26.79, 53.99, 100.52, 84.58, 50.72, 56.79, 43.7, 58.44, 115.38, 118.69, 6.48, 88.89, 36.42, 74.6, 15.27, 94.83, 173.98, 191.05, 32.67, 66.48, 206.07, 193.91, 40.46, 64.63, 134.99, 71.06, 118.36, 94.83, 37.3, 6.48, 68.53, 95.58, 121.38, 99.6, 20.23, 210.54, 59.06, 50.72, 81.95, 46.53, 58.12, 16.13, 139.78, 50.72, 56.79, 3.24, 58.2, 57.28, 68.78, 99.6, 91.44, 70.59, 106.95, 34.14, 41.49, 47.56, 45.59, 86.26, 57.53, 62.3, 189.53, 141.31, 72.94, 72.72, 37.3, 79.74, 85.81, 58.2, 69.11, 63.6, 103.59), N_rotb = c(0.31, 0.29, 0.23, 0.21, 0.29, 0.27, 0.17, 0.07, 0.16, 0.29, 0.27, 0.26, 0.15, 0.12, 0.28, 0.08, 0.14, 0.33, 0.08, 0.1, 0.11, 0.13, 0.17, 0.17, 0.06, 0.23, 0.18, 0.21, 0.06, 0.22, 0.25, 0.16, 0.08, 0.12, 0.24, 0.13, 0.19, 0.24, 0.44, 0.16, 0.2, 0.26, 0.16, 0.3, 0.24, 0.19, 0.05, 0.07, 0.27, 0.31, 0.29, 0.04, 0.06, 0.23, 0.08, 0.13, 0.15, 0.29, 0.15, 0.07, 0.22, 0.22, 0.14, 0.33, 0.19, 0.15, 0.28, 0.2, 0.15, 0.29, 0.06, 0.24, 0.23, 0, 0.29, 0.15, 0.18), log_P_eff_calc = c(-5.3, -4.89, -5.77, -5.91, -4.58, -4.39, -4.63, -4.47, -5.64, -5.85, -5.2, -5.13, -4.57, -4.89, -5.11, -5.87, -4.38, -5.55, -4.69, -4.78, -4.46, -4.77, -5.83, -6.55, -4.45, -5.27, -6, -5.13, -4.57, -4.44, -5.79, -4.59, -5.62, -4.94, -4.78, -4.28, -5, -5.09, -5.87, -5.27, -4.67, -6.79, -5.37, -4.99, -5.15, -5.09, -4.49, -4.65, -6.97, -4.84, -4.45, -4.42, -4.6, -5.02, -5.3, -5.31, -6.37, -5.5, -5.05, -4.54, -4.57, -4.5, -4.46, -5.6, -5.29, -5.07, -6.56, -6.06, -4.85, -5.36, -4.53, -5.35, -4.82, -5.23, -5.29, -4.95, -5.43), residuals = c(-0.53, 0.28, 0.71, -0.24, -0.04, -0.08, 0.19, -0.05, 0.24, -0.59, 0.39, 0.61, -0.53, 0.48, 0.42, -0.85, -0.32, -0.34, 0.1, 0.31, -0.21, 0.02, -0.71, 0.43, 0.13, 0.24, -0.8, -0.3, -0.2, -0.2, -0.48, 0.15, -0.44, 0.28, 0.5, -0.57, 0.31, 0.06, -0.34, 0.56, 0.09, 0.87, -0.79, 0.4, -0.26, 0.26, -0.03, -0.06, 0.01, 0.16, -0.06, -0.19, 0.03, 0.24, -1.06, 0.86, 0.12, -0.55, 0.69, 0.17, -0.01, 0.02, -0.23, -0.71, 0.5, 0.14, 0.79, -0.27, 0.03, -1.02, 0.19, 0.5, 0.22, -0.14, -0.05, 0.27, 0.27)), row.names = c(NA, -77L), class = c("tbl_df", "tbl", "data.frame" ))

ターゲット変数はlog_P_eff_exp

拡散速度の対数（cm / sで測定）です。

予測リスト：

log_DはpH = 7.4での分配係数です。
rgyr-回転半径;
rgyr_d-動的回転半径;
HCPSA —高度に帯電した極性表面の面積。
TPSA-極表面のトポロジカルエリア。
N_rotb- 回転リンクの数。

予測子の分布とペア相関を考慮します。

 GGally::ggpairs(df, columns = c(3:8), diag = list(continuous = "barDiag"))

変数rgyr

とrgyr_d

、およびrgyr

とrgyr_d

、予測できるほど強く相関しています。どちらの場合も、変数のペアは同じ物理量を計算する異なる方法であるためです。

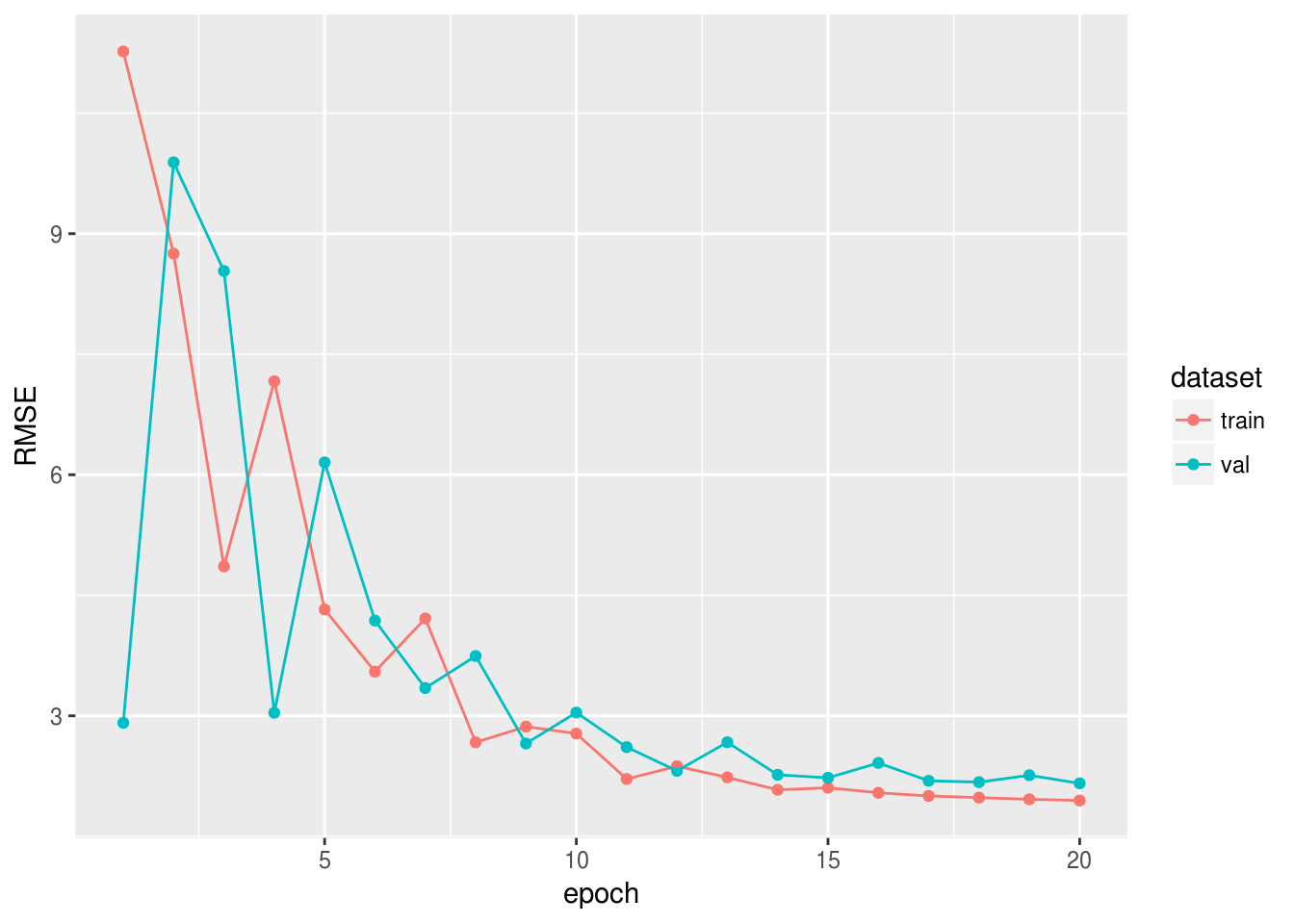
前の例と同じニューラルネットワークをトレーニングしてみましょう。 , .

 set.seed(42) train_ind <- sample(1:77, 60) x_train <- as.matrix(df[train_ind, 2:8]) y_train <- unlist(df[train_ind, 9]) x_val <- as.matrix(df[-train_ind, 2:8]) y_val <- unlist(df[-train_ind, 9]) data <- mx.symbol.Variable("data") fc1 <- mx.symbol.FullyConnected(data, num_hidden = 1) linreg <- mx.symbol.LinearRegressionOutput(fc1) initializer <- mx.init.normal(sd = 0.1) optimizer <- mx.opt.create("sgd", learning.rate = 1e-6, momentum = 0.9) logger <- mx.metric.logger() epoch.end.callback <- mx.callback.log.train.metric( period = 4, #  ,     logger = logger) n_epoch <- 20 model <- mx.model.FeedForward.create( symbol = linreg, X = x_train, y = y_train, ctx = mx.cpu(), num.round = n_epoch, initializer = initializer, optimizer = optimizer, eval.data = list(data = x_val, label = y_val), eval.metric = mx.metric.rmse, array.batch.size = 15, epoch.end.callback = epoch.end.callback)

, RMSE :

 rmse_log <- data.frame(RMSE = c(logger$train, logger$eval), dataset = c(rep("train", length(logger$train)), rep("val", length(logger$eval))), epoch = 1:n_epoch) library(ggplot2) ggplot(rmse_log, aes(epoch, RMSE, group = dataset, colour = dataset)) + geom_point() + geom_line()

次のメッセージでは、実際のデータの分類問題を解決し、他の品質指標と早期停止の使用についても検討します。

Rとmxnetを使用した深層学習。 パート1.作業の基本

内容：