1.はじめに
集合状態を形成する複雑な非線形動的システムの挙動の最も一般的なパターンを理解するための理論的アプローチに基づく方法が提示されています。 レビュー[1]では、フラクタルオブジェクトを使用して、臨界状態または集合状態に対する自己一貫性のある欲求を示す非線形動的システムを記述するための多くの非標準的なアイデアを紹介しています。 集合状態の近くでは、自由度の数は最小になります。 空間のトポロジーの言語では、これは、単純なシステムで集団状態をモデル化する離散的な不浸透性領域の出現により、空間のフラクタル次元が減少することを意味します。
したがって、非線形システムの複雑さは空間の複雑さにも引き継がれます。 同時に、乱流問題から人工知能（自己組織化）までの非線形システムの記述における幾何学的アプローチの普遍性が示されています。 これらのアイデアの開発において、この記事では、カントールダストフラクタルに基づいてフラクタル多様体を構築する例を示します。
初期の非ガウスデータをガウスに変換する計算方法を提案します。これにより、大きなデータセットの構造的特徴をさらに定量的に比較できます。
2.計算方法
定量的な比較を可能にする非ガウスデータの変換値は、ソースデータの値の線形変換に関して不変である必要があります[2]。 この問題には、順序付けられた奇妙なデータと、非線形性が明示されている近傍を考慮したソリューションのみがあります。 論文に示されているように、変換は、非線形性の発現の定量的比較が発生する近傍のサイズに関して繰り込み群不変性を持たなければなりません。
以下は、定量的な比較を可能にする信号対雑音比の式を導出するための重要な手順です。 Cantorダストフラクタルまたは任意の値0 <q <1（Cantorセットの古典的なフラクタルq = 2/3）の等比数列の形式は次のとおりです。
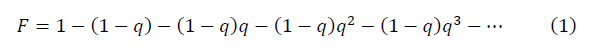
フラクタル多様体を構築するための次の方法が提案されています。 n = 5の5つの順序付き数値の任意のセットに対するフラクタル多様体
形式は次のとおりです。
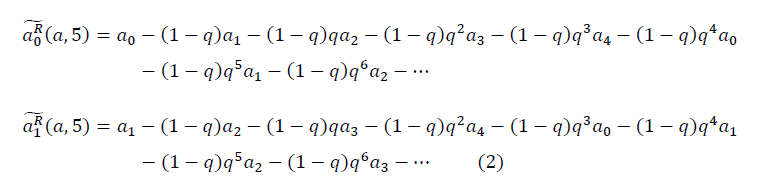
各フラクタルサイクルm（m→∞）では、新しい数値が表示されます
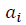非ガウスデータnのサンプルから、さらに閉ループに沿って。 回路バイパスの左右方向を区別します。 一般的な形式：
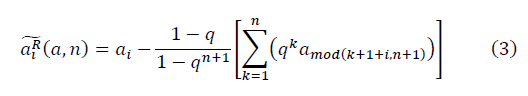
同様に
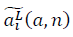判明した：
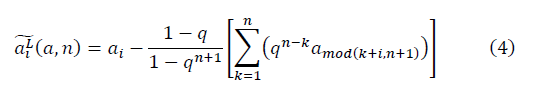
以下、Mathcadという表記の式。
多くの
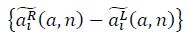そして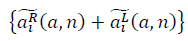 
フラクタル多様体を形成します。 信号対雑音比の式が決定されます。
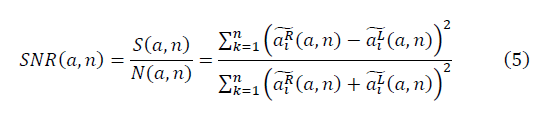
ガウス関数の一意性は、この方法の実際の応用の基礎となるベッセルであり、これらの関数の定義（5）の信号対雑音比SNRはnの値に依存しないことです。 実データには、相互相関によって引き起こされたランダム効果と集合効果の両方が含まれます。 ベッセル関数の有限系列（系列の約3〜7メンバー）によるデータの近似では、ランダムな変動の寄与のみが残ります。 有限フーリエ級数によるデータの近似とそれに続くSNR変換により、集団効果を強調できます。
非ガウス半波データをモデリングする場合
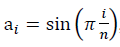、有限フーリエ級数によるデータの予備近似を伴う計算で使用されます。nの十分に大きい値に対して、信号対雑音比の表現は次の形式になります。
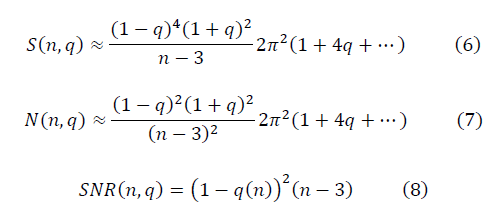
正規化グループ不変性条件SNR（n、q）を満たす必要があります。これにより、奇妙なデータがガウスデータに近づきます.n→n 'が変化すると、q→q'変換が行われ、SNR（n、q）（8）の値は非正規化グループメソッドで変更されません。 繰り込みグループ不変性の要件は、次の条件を満たしている場合に満たされます。
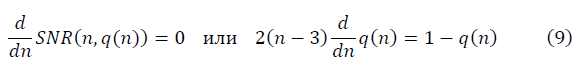
微分方程式の解の形式は次のとおりです。
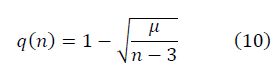
定数値μの選択により、信号対雑音比のスケールが決まります。
nの値が大きい場合、フラクタル多様体の長さパラメーターの漸近的挙動
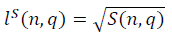そして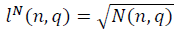 
半波モデルで 
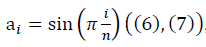、q（n）（10）の繰り込み群方程式を考慮すると、形式は次のようになります。
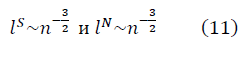
n数の閉ループを通過する方向を考慮して構築されたフラクタル多様体のKolmogorov [3]によるHausdorffフラクタル次元：
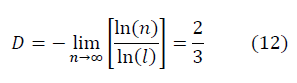
ガウス数の平均：
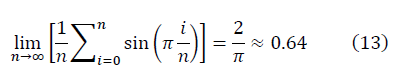
D = 2/3のコルモゴロフ平均とは異なります
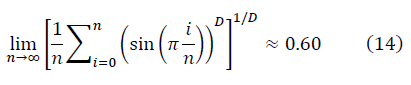
整数pが1より大きい場合、次数pの半波は、次元D = 2/5のフラクタル多様性を生成します。
フラクタル多様体法の実例として、漸近挙動に正規化されたガウス集合に近い二項係数の計算が行われます。
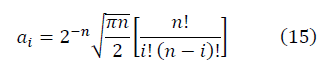
nの値が十分に大きい場合、信号対雑音比の式は次の形式になります。
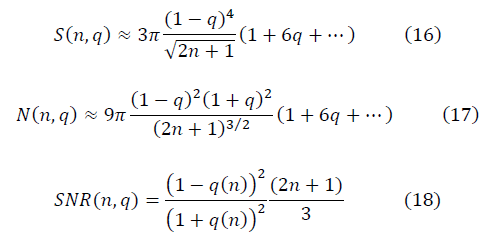
q（n）の繰り込み群方程式：
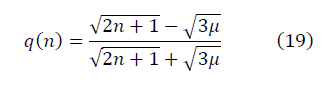
正規化された二項係数のフラクタル次元D = 4/5。
計算でよく使用されるガウス数に関する非ガウスデータの平均の選択は、一意ではありません[2]。 平均値自体だけでなく、平均値を計算するための式の形式も、奇妙なデータによって決まります。 フラクタル多様体法により、小さなスケールを機器として使用して、構造のこのようなよく知られている特性を平均値としてより正確に決定できます
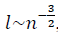ユークリッドスケールと比較して 
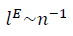そして、定性的に新しい構造的特性-SNRによって決定されるデータの集合状態（自己組織化）のレベルを識別します。
したがって、非ガウスデータのサンプル数nに対するSNRの依存性の出現は、非ガウスデータの相互相関の存在によって説明されます。 Cantorダストフラクタルのqパラメーターの導入とSNRに関する繰り込み群不変性法の適用により、SNRの定義におけるデータ相関の度合いであるガウスデータの従来の分析（5）に進むことができます。
式（24）-（26）を使用して、q = 0で予備計算が実行されます。 計算の予備段階では、順序付けられたデータの異なるセットを比較するときに、データセットの最大集合状態を提供する記述子n（cr1）、n（cr2）のクリティカルサイズが取得されます。 その後、意味が受け入れられます
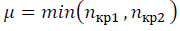式（10）の-3および値が指定されている 
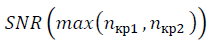繰り込み群の不変性を考慮（20）-（23）。 異なるデータセットのSNR値の比較は、同じμスケールで実行された計算で正しいです。 ピーク値 
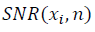変数xのデータ内の構造の存在を特徴付け、集合状態の近傍を示します。 臨界状態または集合状態の概念は、強い相関を持つ自由度のクラスターを示す、奇妙な速度論のアプローチに特徴的です。 集団状態の近傍でのシステムの挙動は普遍的であり、相関を引き起こす相互作用の性質[1]、および相互相関がない場合のランダム変数の分布の普遍性に依存しません。
単位ステップでの順序付きデータの通過中の有限フーリエ級数と記述子サイズnの近似パラメーターは、目的関数の最大条件（システム内の最大集団状態）から決定されます。
行列形式では、信号対雑音比の非正規不変式は次のとおりです。
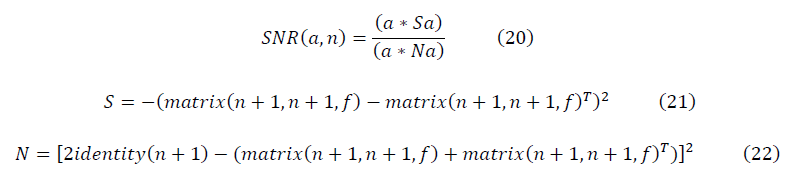
どこで
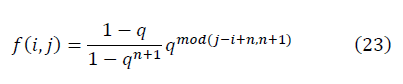
式（11）〜（14）による計算の結果は、式（3）〜（5）による初期計算の結果と同等ですが、アルゴリズムのコンパイルは可能です。
K = n / 2 + 1の一意の順序付けられたスペクトルデータからの計算では、対称ベクトルが構築されます。
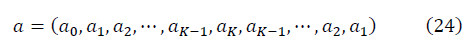
十分に大きいKの場合、行列SとNの対称性を考慮して、くりこみ群不変性の条件が満たされ、q = 0のとき、信号対雑音比の式は次の形式をとります。
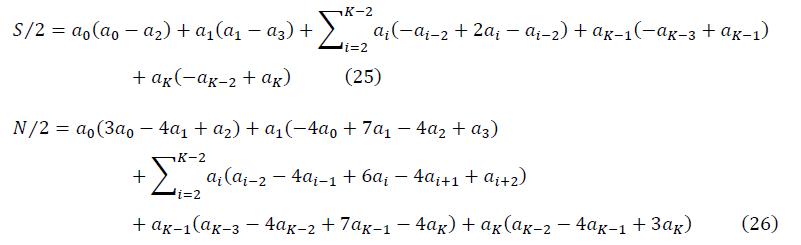
SNR値を順序付けスケールと比較すると、スケールは記述子Kのサイズだけ左にシフトします。有限フーリエ級数kによる予備近似の順序付けられたデータセットは、単一のステップで記述子サイズKによって渡されます。 計算済み
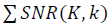データセット内のすべてのポイントの通過によって。 目的関数は次のように定義されます 
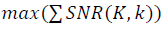パラメーターKおよびkを列挙するとき。 既に述べたように、異なるデータセットのSNRの構造特性の正しい比較は、繰り込み群の不変性を考慮して、単一のスケールμで実行する必要があります（（20）-（23））。 センチメートルとインチで行われた測定値を比較するように。
計算方法は、高解像度で取得された大きなデータセットに使用されます。これにより、繰り込み群の不変性を維持しながら、比較スケールμを大きくすることができます。 大きさの順に、配座異性体の問題では、X線回折分析のスペクトル内のデータの総数は2250値であり、特定の解像度に対する最適な記述子サイズはK = 585であり、有限フーリエ級数の最大高調波はk = 3です。
3.結論
この方法は、領域間の自由度の強い相関がある領域の決定や、大量の順序付けされたデータの相関度の定量的比較に適用できます。 たとえば、Hartree-Fock近似が適用できない場合。 データ処理結果の解釈は、1次元空間の集合状態または臨界状態[1]をモデル化するフラクタル多様体の構築に基づいています。 解釈は、さまざまなタスクの集合状態を説明する用語の曖昧さによって複雑になります。
化学の集合状態は、分子フラグメントの柔軟性または可動性です。 酵素の活性中心の柔軟性の仮定に基づいた、生物活性の発現における誘導対応のコシュランド仮説は、酵素の作用を十分に説明しています。 基質が酵素の活性中心に近づくと、酵素分子内でコンフォメーション再編成が同時に起こり、多数の自由度に影響します。 計算法を3つの配座異性体のスペクトルに適用すると、生物活性を特徴とする配座異性体の集合的効果が大幅に増加することがわかります。 同様に、生物活性の発現により、集合的効果の例は、高弾性領域で異なる分子量を持つポリマーの熱機械曲線法で示されます。
線形変換および繰り込み群の不変性に関する不変性の特性を考慮して、非ガウスデータの大きなセットにユニバーサル変換式を適用すると、集団状態を定量的に比較することができます。 この方法は、初期の非ガウスデータの予備変換、データの相互相関の程度の比較、および構造とプロパティ間の定量的関係の検索でデータサイエンスの問題を解決するために使用されます。
4つのポイントについて、SNRは、コンピュータービジョンのエッジ検出の最も初期のアルゴリズムの1つであるRobertsクロスオペレーターの式と一致します。
4.文学
- ゼレニーL.M.、ミロヴァノフA.V. 物理科学、フラクタルトポロジ、およびストレンジカイネティクスの進歩：パーコレーション理論から宇宙電気力学の問題まで-2004、No. 8、P. 809-852
- オルロフA.I. 適用された統計。 -M .:試験、2006 .-- 574
- コルモゴロフAN、推移的動的システムの新しい計量不変量とルベーグ空間の自己同型、-1958、ソ連科学アカデミーの報告書、No。5、P。861-864