リチャードハミング：第15章デジタルフィルター-2

「このコースの目標は、技術的な未来に向けて準備することです。」

こんにちは、Habr。 「You and Your Work」という素晴らしい記事（+219、2372のブックマーク、375kの読み取り）を覚えていますか？



そのため、ハミング（はい、はい、自己チェックおよび自己修正ハミングコード ）には、彼の講義に基づいて書かれた本があります。 男性がビジネスを話しているので、私たちはそれを翻訳します。



この本はITだけでなく、信じられないほどクールな人々の思考スタイルに関する本です。 「これは単なる肯定的な思考の責任ではありません。 素晴らしい仕事をする可能性を高める条件を説明しています。」



すでに17（30のうち）の章を翻訳しています。 そして、 私たちは紙版に取り組んでいます。

第15章デジタルフィルター-2

（翻訳のおかげで、Andrei Pakhomov、「前の章」で私の電話に答えてくれました。）翻訳を手伝いたい人は-個人のメールまたはmagisterludi2016@yandex.ruに書いてください



デジタルフィルターが最初に登場したとき、それらは一種の古典的なアナログフィルターと見なされていました。 人々はそれらを根本的に新しく、既存のものとは異なるものとは考えていませんでした。 最初のコンピューターではまったく同じエラーが一般的でした。 コンピューターはただの計算機であり、機械が計算できるものはすべて人が数えることができると疲れ知らずに言われました。 この声明では、手作業と機械作業の速度、精度、信頼性、コストの違いを無視しています。 通常、1桁（10倍）の量の変化は根本的な変化につながり、コンピューターは手動計算よりも何倍も高速です。 違いはないと主張した人々は、コンピューターの開発に重要なことをしませんでした。 重要な貢献をした人は、コンピューターの新しいもの、まったく同じように評価されるべきものを、同じ古い計算機のようにではなく、ほんの少しだけ速く見たはずです。



これはよくある、無限に繰り返される間違いです。 人々は常に、新しいものは古いものと非常に似ていると考えたいと思っています。 彼らは心だけでなく、身体にも安らぎを求めるのが好きです。そのため、彼らは鼻の下に生じる新しい産業に大きく貢献する機会から身を守ります。 新しいと呼ばれるものすべてが実際にそれであるわけではなく、場合によっては何かが本当に新しいかどうかを判断するのが困難です。 ただし、「ここには新しいものはありません」という一般的な設定はバカです。 何かが新しいと呼ばれるとき、それは単に古いものの改善であると考えて急いではいけません-それはあなたが何か重要なことをする素晴らしい機会になる可能性があります。 しかし、これも実際には新しいものではないかもしれません。



原始的なコンピューターの時代に使用した最初のデジタルフィルターは、最初に3倍の平滑化を実行し、次に5倍の平滑化を実行しました。 平滑化公式を思い出して、3倍平滑化の伝達特性は次のように定義されます







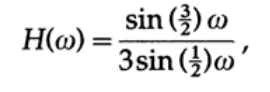
簡単に描画できます（図15.I）。 5倍の平滑化の場合、伝達特性はまったく同じに見え、3/2のみが5/2に置き換えられ、簡単に描画することもできます（図15.I）。 連続する2つのフィルターの場合、全体の伝達特性は明らかに伝達特性の積です（それぞれが対応する周波数の伝達特性で入力信号-独自の関数を乗算します）。間隔に3つのゼロがあり、最終値は1/15になります。 さらなる研究により、周波数の上半分は、3つの数値の合計、次に5つの数値の合計を計算する単純なコンピュータープログラムによってかなり適切にフィルター処理されたことがわかります。これは、すべての除算演算を最後に転送し、1つの乗算に置き換える一般的なコンピューターの手法です-結果に1を掛けます/ 15。



これで、デジタルフィルターが数値の配列から特定の周波数をどのように正確に除去するのか疑問に思われるかもしれません。







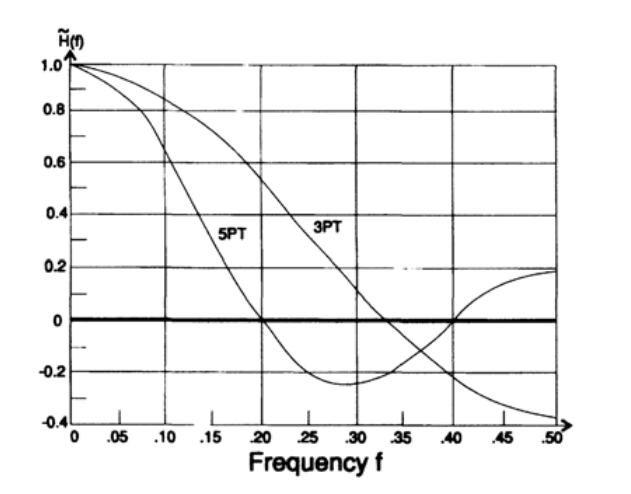
図15.I



したがって、2つの係数のみを持つ単純なフィルターを合成することをお勧めします。これが、伝達関数に厳密に2つの制限を課すことができる理由です。 理論的には、周期的な周波数を使用しますが、実際には周波数を使用します。 これらの2つの値は、次のように相互接続されます。







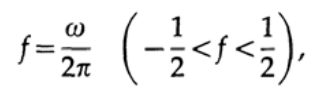
フィルターの制限を次のように定式化します：周波数f = 1/6の場合、フィルターの伝達特性の値は1に等しく（この周波数はフィルターを変更せずに通過する必要があります）、周波数f = 1/3の場合、伝達特性の値はゼロになります。



私の簡単なフィルターは次のとおりです







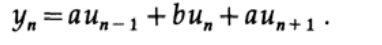
ここで、aおよびbは、値を決定しようとするパラメーターです。



exp（2pifn）を固有関数に代入して、伝達特性を取得します。



便宜上n = 0に置き換えて、次の連立方程式を取得します。







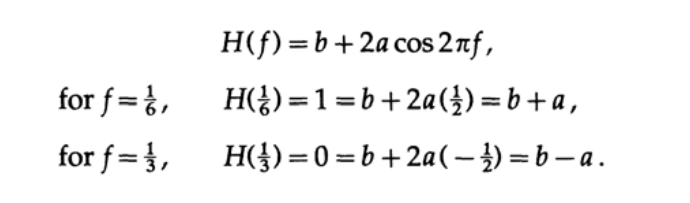
この連立方程式の解はa = b = 1/2であり、目的の平滑化フィルターは単純な式です。







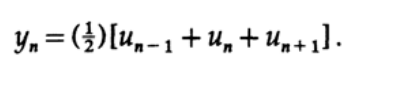
つまり、フィルター出力での値は、フィルター入力での3つの連続した値の合計を3で割った値に等しくなります。 フィルター出力の値は、入力データの中心値の反対です。



いくつかのテストデータをフィルター入力に渡しましょう。 1/6の周波数で送信される信号として、同じ時間間隔（n = 0、1、2、...）で取得した同じ周波数のコサイン関数の値を使用します。 同様に、1/3の周波数で信号値をシミュレートします。 特定の瞬間にフィルターの入力に供給される信号の値は、同じ瞬間にこれらの信号の値の合計に等しくなります。







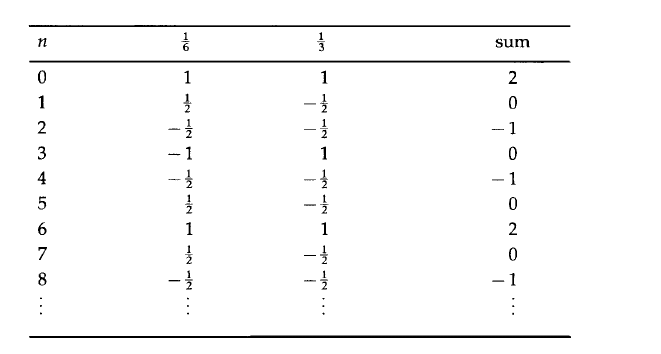
次に、この信号をフィルターに渡します。 得られたフィルター式に従って、列の3つの連続した数値の合計を2で除算します。最初の列でこの操作を実行すると、フィルターがテーブル内で1行下に移動するたびに、入力に適用された関数が再現されることがわかります（回1）。 2番目の列をフィルターに通すと、出力の値が常にゼロであるか、入力関数の値に固有値0が掛けられていることがわかります。最初の2つの合計である3番目の列のフィルター処理では、最初の周波数をスキップして2番目の周波数を停止する必要があります。 つまり、3番目の列をフィルタリングすると、最初の列が取得されます。 ゼロに等しい周波数の信号を入力しようとすることができます。 この場合、値ごとに正確に3/2を取得する必要があります。 周波数f = 1/4を試す場合、入力値に½（f = 1/2の伝達特性の値）を掛けた値を取得する必要があります。



デジタルフィルターが動作しているのを見ました。 フィルターは、入力信号をすべての合成周波数に分解し、各周波数に独自の固有値（伝達特性）を乗算し、それらを合計して出力で値を取得します。 これはすべて、1つの単純な線形フィルター式で行われます！

フィルター合成の問題に戻りましょう。 多くの場合、変更なしで送信する周波数（固有値1）と停止する周波数（固有値0）の間で急激に低下する伝達特性を取得する必要があります。 ご存じのように、このようなギャップのある関数はフーリエ級数で拡張できますが、この級数には無限の数の項が含まれます。 それにもかかわらず、実用的なフィルターを取得したい場合、そのようなメンバーの数は限られています。 平滑化フィルターの2k + 1項では、k + 1個の自由係数のみを取得できるため、対応する余弦の合計にk + 1個の通常条件のみを重ね合わせることができます。



目的の伝達関数を一連の余弦に単純に分解し、その中の項の数を減らすと、最小二乗法による伝達特性の近似が得られます。 ただし、ブレークポイントでは、最小二乗近似では期待どおりの結果が得られません。

不連続点で何が表示されるかを理解するには、ギブス効果を調べる必要があります。 まず、定理を思い出してください。一連の連続関数がセグメント上で均一に収束する場合、シリーズの合計はこのセグメント上で連続です。 しかし、近似する関数は連続ではありません。通過帯域と障害帯域の分離点にジャンプ（ギャップ）があります。 使用するシリーズのメンバーの数は関係ありません。 均一な収束ができないため、特異点（ブレークポイント）の近くに大きなサージが見られることが予想されます。 シリーズのメンバーの数が増えても、サージの大きさはゼロになる傾向はありません。



ここに別の自転車があります。 Michelson-Morleyの実験で知られるMichelsonは、最大75項までのフーリエ級数の展開係数を決定できるアナログデバイスを構築しました。 このデバイスにより、係数から関数に切り替えることもできました。 マイケルソンがフーリエ級数の係数によって関数を復元したとき、彼は急上昇を発見し、なぜこれが起こっているのか地元の数学者に尋ねました。







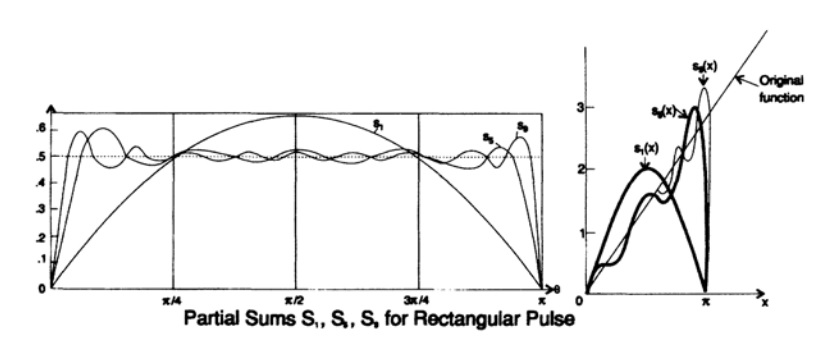
図15.2



彼らは皆、理由は彼の装備にあると言った-そして、彼は広く実験的な実験者として知られていたという事実にもかかわらず。 そして、イェール出身のギブスだけが問題を聞いて研究した。 最も単純で最も簡単なアプローチは、通常の関数をギャップ付きで拡張することです。たとえば、有限数の項を持つフーリエ級数で、元の関数を再構築し、最初の最大点とこの点での関数の値を見つけます。







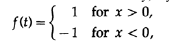
グラフ15.2では、フーリエ級数のメンバーの数が無限になる傾向がある限界で、0.0849のサージ、または8.949％のサージを検出できます。 多くの人がギブス効果を発見（実際に再発見）する機会がありましたが、努力したのはギブスでした。 これは、私が常に頑張っていることのもう1つの確認です。 パストゥールが言ったように、「フォーチュンはこの準備ができている人にだけ微笑む」。 今回、一流の科学者の話を聞いて問題の解決を手伝う準備ができていた男性が有名になりました。



この効果が再発見されたことに注目しました。 そうです。 1850年のコーシー教科書では、2つの矛盾するステートメントを見つけることができます。（1）連続関数の収束シリーズは連続関数に収束し、（2）フーリエ級数の不連続性を持つ関数の展開。 一部の人々は問題を整理し、均一な収束の概念を導入する必要があることを発見しました。 つまり、ギブス効果は、フーリエ級数だけでなく、一連の連続関数への展開に現れます。 この事実は個人に知られていましたが、広い用途は見つかりませんでした。 一般的な場合、一連の直交関数に展開する場合、バーストサイズは、分解された関数の不連続が正確にどこにあるかに依存します。 これにより、フーリエ関数が他の直交関数と区別されます。フーリエ展開の場合、バーストの大きさは不連続性の位置に依存しません。



フーリエ級数の別の特性を思い出してください。 関数が存在する場合、係数は1 / nとして減少します。 関数が連続的である場合（極値の両端の値が同じで、導関数がこの点に存在する場合、係数は1 / n ²として減少します。1次導関数が連続し、2次導関数が存在する場合、1 / n ³として減少し^ます。したがって、収束率級数は実数の軸に位置する関数によって決定されます。これは、テイラー級数には当てはまりません。テイラー級数の収束は、複素平面にある特異点によって決定されます。



フーリエ変換を使用してシリーズの最初のメンバーを取得し、デジタル平滑化フィルターの設計に戻ります。 ご覧のとおり、最小二乗近似には特異点で問題があります-伝達関数の不快な爆発は有限数の項で構成され、使用するシリーズの項の数は関係ありません。







図15.3



最初に、スプラッシュを除去できるLanczosウィンドウ（「長方形ウィンドウ」または「長方形関数」とも呼ばれます）を検討します。 Lanczosは次のように推論しました。「出力信号に存在する最高周波数の関数の周期に等しい長さの間隔で出力関数の値を平均すると、リンギングが大幅に減少します。」 これをより詳細に検討するために、フーリエ展開の最初のN個の調和関数を取得し、間隔全体から長さ1 / Nのポイントtを中心とした対称間隔で積分を取得します。 平均化のための積分を







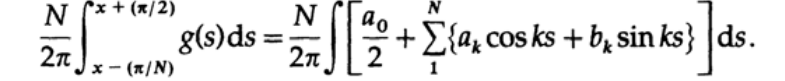
それでは積分を見てみましょう。







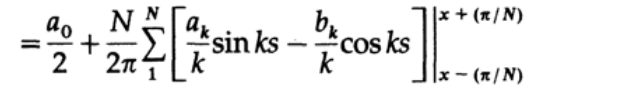
積分区間の境界に正弦と余弦の差の式を適用します：







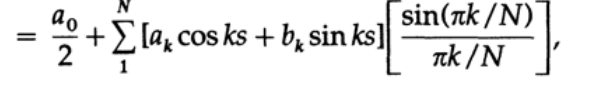
そして、初期係数にいわゆるシグマ因子を掛けたものを取得します。







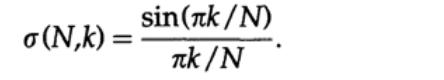
このような数値のシーケンスをkの関数として考えると（Nは固定され、フーリエ級数の拡張の調和数に等しい）、k = 1の場合、シグマ係数は1であり、kが増加すると、シグマ係数はk = Nでゼロに減少します。 つまり、ウィンドウ関数の別の例です。 ランチョスウィンドウを適用すると、バーストが0.01189（7倍）に減少し、最初の最小値が0.00473（10倍）に減少します。これは、ギブス効果の大幅な減少ですが、完全な減少ではありません。



しかし、この分野での私の冒険に戻りましょう。 あなたのように、不連続点では、有限数のメンバーを持つフーリエ級数の展開は、不連続点の左右に取られた2つの制限の平均に等しいことを知っていました。 有限の離散的なケースについて言えば、通過帯域でユニティを取り、減衰帯域でゼロにする代わりに、½を中間値として使用する必要があると結論付けました。



そして、転送特性は次のようになり始めました







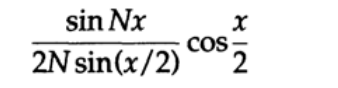
そして今、追加の要因があります（再び周波数表記に戻ります）







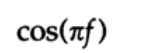
分母N + 1がNになったように、シリーズの正弦項のN + 1はNになりました。明らかに、ローパスフィルターのこの伝達特性は、ナイキスト周波数で減衰し、さらにその上にあるすべての周波数を抑制するため、ランチョスの伝達特性よりも優れています。 私は三角関数シリーズの本に目を通しましたが、そのうちの1つだけ-Sigmundの2巻の本-では、そのようなシリーズの言及を見つけましたか？それは修正されたシリーズと呼ばれていました。 理論の研究にもっと時間を費やせば、顕著な結果が得られることはまったく必要ありません。 このようなシリーズ展開の修正を自分で受けたので、私は自然にフーリエ級数の係数のさらなる変化について考え続けました（まだどの係数とどのように変化するかを把握しなければなりませんでした）。 要するに、「ウィンドウ関数」が何であるかをより明確に理解し、その機能のより詳細な研究に徐々に近づきました。



フーリエ級数の結合によるギブス現象への3番目のアプローチがあります。 g（x）を（この場合、中立変数xを使用する正当な理由があります）とします。







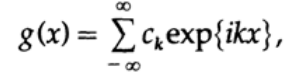
そして別の機能は







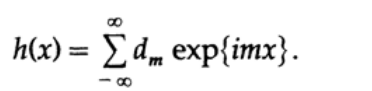
合計と差g（x）とh（x）は、係数の合計と差を持つ対応する系列に明らかに等しくなります。



状況は仕事によって異なります。 明らかに、再び指数の合計を取得し、n = k + mを決定すると、示された係数を取得します。







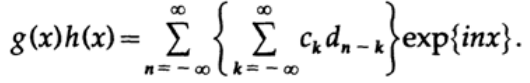
メンバの合計であるexp {inx}の係数は、係数の元の配列の畳み込みと呼ばれます。



配列c _kでゼロに等しくない少数の係数のみ、たとえば0に関して対称性のあるノットを使用する場合、係数について次の式が得られます。







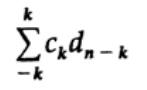
これがデジタルフィルターの初期定義です！ したがって、フィルターは2つの配列の畳み込みであり、対応する関数の単純な乗算です。 等式の一方の乗算と他方の畳み込み。



この観測の実際の使用例として、かなり一般的なケースを示します：データの無限配列がありますが、記録できる値の数は限られています（たとえば、星の観測中に望遠鏡をオンまたはオフにする）。 このような関数u _nは、2N + 1以外のすべての値がゼロに等しい長方形の窓を通して観察されます。 言い換えると、観測の瞬間、窓関数は1であり、残りの時間は0です。



記録された値によって元の配列のフーリエ展開を計算しようとすると、元の配列の係数と窓関数の畳み込みを計算する必要があります。







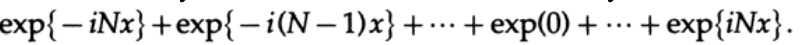
原則として、面積が1のウィンドウを取得するため、（2N + 1）で除算する必要があります。 結果の配列は、第1項exp {-iNx}と累進exp {ix}の分母を持つ等比数列です。







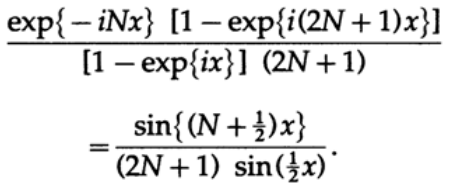
x = 0の場合、式の値は1です。他の場合、式の値は分子のサインにより急速に変動し、分母のサインの増加によりゆっくりと減衰します（xは区間（-π、+π）に属します。したがって、光学の典型的な回折画像が得られました。 。



離散化まで連続する信号の場合、状況は同様の方法で発生します。信号を観測する長方形のウィンドウのみが一般的な変換を行います（詳細はすべて無視します）。







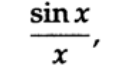
また、ステップ関数との畳み込み（不連続性）は、ギブス効果の出現につながります（図15.II）。 したがって、異なる光のギブス効果によるバーストが見られました。



かなり複雑な三角変換により、関数の離散化とそれに続く観測間隔の制限、および観測間隔の制限と後続のサンプリングにより、同じ結果が得られることがわかります。 理論でも同じことが言えます。



離散ランチョスウィンドウの2つの外部係数を1から½に単純に変更すると、ウィンドウ関数が向上します。ランチョスウィンドウはすべての係数をシグマファクターによって変更しますが、その形状はエッジに角度を持っています。つまり、関数の周期性により、1次導関数に2つの不連続性があるため、収束が遅くなります。







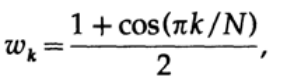
フーリエ級数の展開の項の重み係数としてレイズドコサインの使用を議論する場合、Lanczosウィンドウ関数に似たものが得られますが、より滑らかで、収束が速くなります。



これを指数形式で記述したので、指数での重み係数は次と等しいことがわかります。







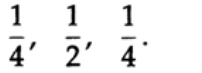
ハンナの窓ができました。これらの係数を使用した時間領域の平滑化は、周波数領域の乗算と同等です。実際、パワースペクトルの研究の最初の段階でハンナのウィンドウを再発見しました。後にジョンチューキーは、ハンがはるかに早く経済のためにそれを使用したことを発見しました。このウィンドウ関数が信号に対して行うことを調べると、信号は急速に減衰しますが、スペクトルの一部が通過するサイドローブがあります。



次に、はっきりとした線のあるスペクトルを処理し、ハンウィンドウを通してスペクトルの他の部分を見ると、サイドローブが多くのエネルギーを伝達できることがわかりました。ハミングウィンドウは、最大のサイドローブを最小にするように設計されています。このウィンドウ関数を使用すると、スペクトル内の1つの顕著なラインを制御できますが、rmsリークが非常に大きくなります。

重み係数を使用してハンウィンドウ関数を「レイズドコサイン」と呼ぶと







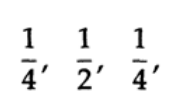
、ハミングウィンドウは「プラットフォーム上のレイズドコサイン」です（図15.IV ）、重み付き











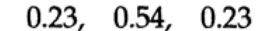
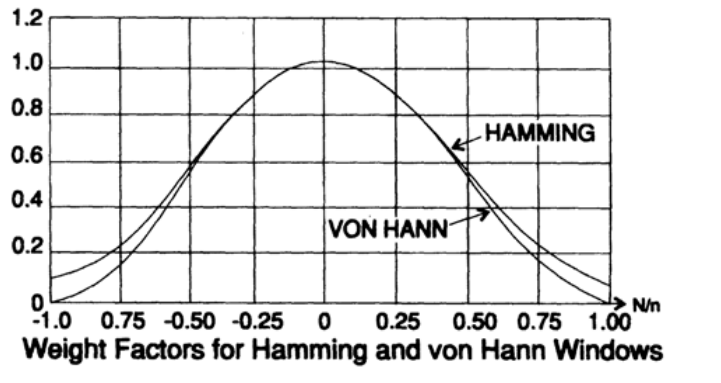
図15.4



実際、重みはデータ配列の長さNに依存しますが、多くの場合、これらの定数のいくつかが使用されます。ハミングウィンドウ関数は、1つの特定の問題を解決するために設計されたものであり、すべての問題に対する普遍的な解決策ではありませんが、その異常な係数に関する謎の雰囲気のために人気があります。ほとんどの場合、ハンナウィンドウ関数を使用することをお勧めします。文献には、それぞれ独自の利点を持つ100種類のウィンドウ関数が記載されている可能性がありますが、それらのどれも、あなたが見たいすべての利点を持っているわけではありません。



その話のすべての複雑さにあなたを捧げるために、私はあなたに別の話をします。私はかつてジョン・テューキーをからかっていました：「あなたは、あなたの名前がワット、アンペア、ボルト、時にはフーリエなどのような小さな文字で書かれているときだけ知られています。」 Tukeyが初めてパワースペクトルに関する研究を書いたとき、彼はプリンストンから電話をかけて、ハミングウィンドウの名前に私の名前を使用できるかどうかを尋ねました。それでもいくつかの抗議の後、私は彼の提案に同意した。本は「Hamming」という名前で出てきました！私だ！



ある意味では、あなたを引用し、あなたに言及して、あなたを有名にするのはあなたの友人です。このようにして、提供された支援に対して報酬が支払われます。したがって、他の人が自分のタスクに対処しようとするときに他の人を助けることをお勧めします。彼らはあなたに仕事の一部を時間内に任せることができ、これはあなた自身でこれを達成しようとするよりも良いかもしれません。現在、協力は複雑なプロジェクトの基礎となっています。孤独の日々はすぐに去ります。チームワークはますます重要な位置を占めているため、チームワークのトレーニングを行い、他の人を助けることができる場所を見つけることをお勧めします。いずれにせよ、重要なタスクで優れた人々と仕事をすることの喜びは、その名声よりも大きな満足をもたらします。逆に、自分自身で重要なタスクを選択するということは、経営陣が支援を提供する準備ができていることを意味します。必要になるかもしれません。



Bell Labsでの長年の仕事を通じて、私は自分の結果を公開することに非常に注意し、他の人のアイデアの泥棒になるような状況を許しませんでした。それどころか、私は他の人に自分の作品を公開することを許可し、彼らが私を共著者として示したいと思っていたとしても-素晴らしい、私は気にしません！チームワークは、他の人とその貢献に注意を払うことを意味します。なぜなら、彼らはそれをまったく異なる観点から見ることができるからです！





継続するには...



誰が翻訳を手伝いたいのか-個人のメールまたはメールに記入してくださいmagisterludi2016@yandex.ru



ちなみに、私たちはまた別のクールな本の翻訳を開始しました- 「The Dream Machine：The History of the Computer Revolution」 ）