リチャード・ハミング：第11章コーディング理論-II

「このコースの目標は、技術的な未来に向けて準備することです。」

こんにちは、Habr。 「You and Your Work」という素晴らしい記事（+219、2442のブックマーク、393kの読み取り）を覚えていますか？



そのため、ハミング（はい、はい、自己チェックおよび自己修正ハミングコード ）には、彼の講義に基づいて書かれた本があります。 男が問題を言うので、私たちはそれを翻訳します。



この本はITだけでなく、信じられないほどクールな人々の思考スタイルに関する本です。 「これは単なる肯定的な思考の責任ではありません。 素晴らしい仕事をする可能性を高める条件を説明しています。」



すでに25（30のうち）の章を翻訳しています。 そして、 私たちは紙版に取り組んでいます。

11.コーディング理論-II

（「前の章」での私の電話に答えてくれた翻訳erosinkaに感謝します。）翻訳を手伝いたい人は-個人のメールまたはメールmagisterludi2016@yandex.ruに書いてください



前の章から2つのことを明確にする必要があります。 まず、送信されたメッセージの平均の長さLをできるだけ短くしたい（リソースを節約するため）。 第二に、どのメッセージが送信されるのかわからないため、これは統計理論によってサポートされるべきですが、以前のメッセージを使用していくつかの統計データを知ることができ、その後の出力は以前のものと似ているかもしれません。 ここで説明できる唯一の理論である最も単純な理論では、メッセージ内の個々のシンボルの出現確率が必要です。 それらを取得するという問題は理論の一部ではありませんが、過去の経験を研究するか、設計しているシステムの将来の使用についての占いを想像することによって得ることができます。



したがって、入力文字siの特定のセットと、その確率piに対して、即座に一意にデコードされたコードが必要です。 最小平均コード長を取得するために、どの長さliを設定する必要がありますか（クラフトの不等式に従う必要がある場合）？ ハフマンはこのコード設計の問題を解決しました。



ハフマンは、次の不等式が最小長のコードに当てはまることを示した最初の人物です。 piが降順の場合、liは昇順である必要があります。







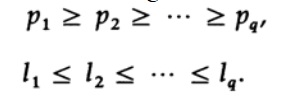
piがこの順序であると仮定しますが、少なくとも1つのペアliはそうではありません。 指定された順序ではない2つの文字に関連付けられている文字を再配置する効果を考慮してください。 順列の前に、式のこれら2つの項のコードLの平均長への寄与







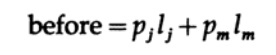
そして再配置後







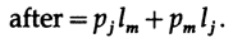
合計Lの他のすべての項は同じままです。 違いは次のように書くことができます







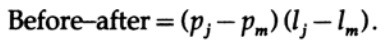
これらの項の1つは負であると想定されているため、2文字の順列の後、コードLの平均長は減少します。 したがって、最小のコード長には、2つの不等式が必要です。



その後、ハフマンは、即座に復号化されたコードに決定木があり、各ノードに2つの出力が必要であることを発見しました。そうでない場合、これは空の試みであるため、同じ長さを持つ最長の文字が2つあります。







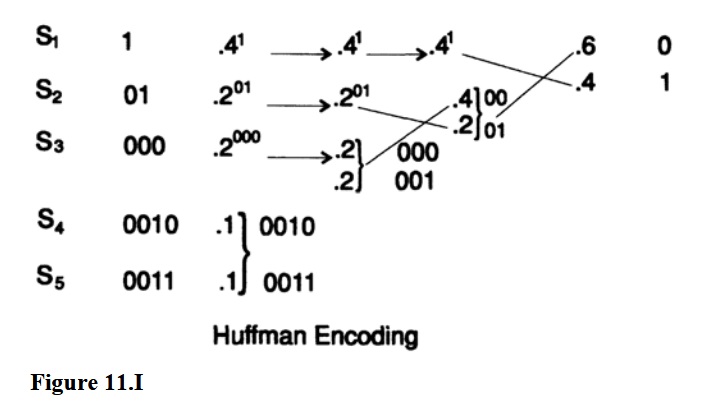
ハフマンコードを説明するために、古典的な例を使用します。 p（s1）= 0.4、p（s2）= 0.2、p（s3）= 0.2、p（s4）= 0.1、p（s5）= 0.1とします。 これを図11に示します。その後、ハフマンは、上記の値に基づいて、頻度が最も低い2つの文字（同じ長さ）を、破棄される最後のビットまでの共通ビットで共通の確率で1文字に結合（結合）できると主張しました。したがって、コードが1文字少なくなります。 （？）これを何度も繰り返して、彼は2文字でシステムに来ました。そのために、コード表現、つまり1文字-0ともう1文字-1を割り当てる方法を知っていました。







さて、反対方向に進むと、各段階で、2つの文字の組み合わせから判明した文字を分離し、同じ先頭ビットを維持しながら、1つの文字と別の文字に0を追加する必要があります-この方法により、最小長Lのコードに到達します、再び図11を参照してください。これは、長さL 'が短い別のコードがあった場合、特定の数だけ平均コード長を変更するステップを実行すると、平均コード長が1未満の2文字になります。 。 したがって、ハフマンコードの長さは最小です。 対応するデコードツリーと共に図11.IIを参照してください。



このコードは一意ではありません。 まず、プロセスの各ステップで、各シンボルに0と1を割り当てることは任意のプロセスです。 第二に、いずれかの段階で同じ確率のシンボルが2つある場合、どちらが最初であるかは問題ではありません。 これにより、場合によってはコードが大きく異なりますが、両方のコードの平均長は同じになります。



結合した用語を可能な限り高くすると、図11.IVの対応するデコードツリーとともに図11.IIIが得られます。 2つのコードの平均の長さは同じですが、コードとデコードツリーは異なります。 最初のものは長く、2番目のものは枝分かれしており、2番目のものは最初のものよりも揮発性が低くなっています。



コーディングシステムの開発では可能な限り平均長が短いコードを使用することが自然な欲求であるため、ハフマンコーディングの仕組みを確認できるように、2番目の例を示します。 たとえば、バックアップストレージ用に大量のデータを保持でき、適切なハフマンコードでエンコードすると、予想されるストレージボリュームの半分以上を節約できることがわかっています。 p（s1）=⅓、p（s2）=⅕、p（s3）=⅙、p（s4）= 1/10、p（s5）= 1/12、p（s6）1/20、p（ s7）= 1/30、p（s8）= 1/30。 まず、確率の合計が1であることを確認します。分数の共通分母は60です。したがって、合計確率を取得します。















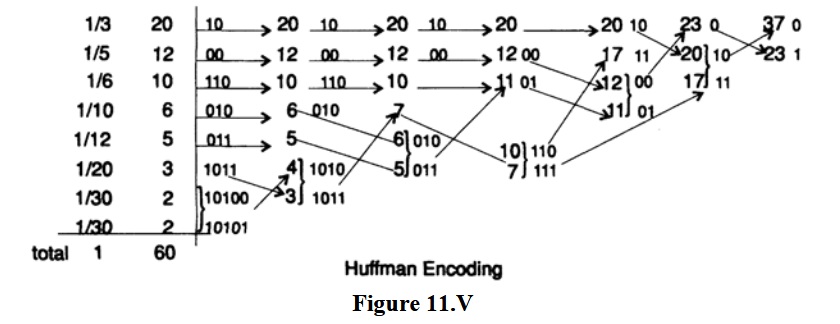
2番目の例を図11.Vに示します。相対値のみが重要であるため、確率の分母で60を省略しています。 文字ごとの平均コード長は？ 計算する







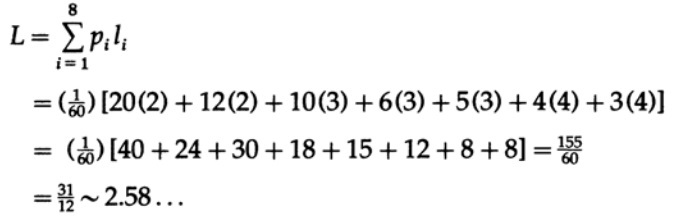
8文字のコードブロックの場合、各文字の長さは3で、平均の長さは3です。これは2.58を超えています



この機械的プロセスが機械にどのように適しているかに注目してください。 ハフマンコーディングの各直接ステップは、同じプロセスの繰り返しです。2つの最小確率を組み合わせ、新しい合計を配列内の適切な場所に配置してマークします。 逆のプロセスでは、マークされたシンボルを取得して分離します。 これらのプログラムはコンピューター用に簡単に作成できるため、コンピュータープログラムはデータsiとその確率piからハフマンコードを計算できます。 実際には、非常に小さな確率でリターンキャラクターを属性付けすることを忘れないでください。そうすることで、メッセージの最後でデコードプロセスを完了できます。 実際、ストレージ用のデータを取得して確率推定値（小さなエラーのみが小さなLの変化につながる）を見つけ、ハフマンコードを見つけ、最初のデコードアルゴリズム（ツリー）をエンコードして送信してからエンコードされたデータを送信できるプログラムを作成できます。これはすべて、人間の介入なしで！ デコードの終了時に、デコードツリーを既に受け取っています。 したがって、プログラムを作成すると、そのプログラムが役立つと思われる場合に使用できます。



ハフマンコードは、使用される可能性が非常に低いため、一部のコンピューターでも命令で使用されていました。 したがって、すべての文字に同じ長さを使用する単純なブロックコーディングと比較して、ハフマンコーディングを使用するときに期待できるLコードの平均長の改善を調べる必要があります。



すべての確率が同じで、正確に2 ^ k個の文字がある場合、ハフマンコーディングの研究により、同じ長さの標準ブロックコードが得られることがわかります。 正確に2 ^ k文字がない場合、それらの一部は短くな​​りますが、それらのほとんどが1ビット短くなるか、またはいくつかが2ビット以上短くなるかを判断するのは困難です。 いずれの場合も、Lの値は同じであり、対応するブロックコードよりも短くなりません。



一方、各piが⅔（最後を除くすべての後続確率の合計）より大きい場合、1文字が1（0）の長さ、1文字が2（10）の長さなどのコンマコードを取得します。終了、同じ長さ（q-1）の2文字：（1111 ... 10）と（1111 ... 11）。 この場合、長さLは対応するブロックコードの長さよりもはるかに短くすることができます。



ルール：ハフマンコーディングは、キャラクターの確率が非常に異なる場合に報われ、それらがほぼ等しい場合には報われません。



ハフマンプロセスに2つの等しい確率が現れると、それらは任意の順序で配置できるため、コードの長さは同じになりますが、コードは非常に異なる場合があります。 2つの等しい確率の場合にどちらの順序を選択するかを尋ねるのは自然なことです。 合理的な基準は、ソース文字と同じ長さのメッセージがエンコード形式でほぼ同じ長さになるようにコードのばらつきを最小限に抑えることです。元のショートメッセージが誤ってロングメッセージでエンコードされないようにする必要があります。 ルールは単純です。テーブルに新しい確率を可能な限り高く挿入します。 実際、わずかに高い確率でシンボルの上に配置すると、バリエーションが大幅に減少し、Lがわずかに増加します。 これは良い戦略です。



すべてのステップを完了した後、ソースのコーディングに進みます（ただし、トピック全体については説明しませんでしたが）。 ノイズをシミュレートしたコーディングチャネルを使用します。 仮定により、チャネルにはノイズがあります。これは、送信中（または保存中）に一部のビットが変更されたことを意味します。 何ができますか？



単一のエラーを見つけるのは非常に簡単です。 （n-1）ビットのブロックには、n番目のビットに、すべてのnビットが偶数1（または必要に応じて奇数、ただし偶数を使用する）になるような値を付加する必要があります。 これは、パリティチェック（奇数）と呼ばれます。



したがって、送信されたすべてのメッセージにこのプロパティがある場合、受信側で完了したかどうかを確認できます。 パリティチェックが失敗した場合、少なくとも1つのエラー、実際には奇数のエラーがあることがわかります。 どの位置でもエラーの可能性が低いシステムを使用するのが賢明であるため、いくつかのエラーの可能性はさらに低くなります。



数学的適合性のために、チャネルにホワイトノイズがあると仮定します。これは、1）nビットのブロック内の各位置は他の位置と同じエラー確率を持ち、2）異なる位置のエラーは無相関、つまり独立していることを意味します。 これらの仮定により、エラーの確率は等しくなります







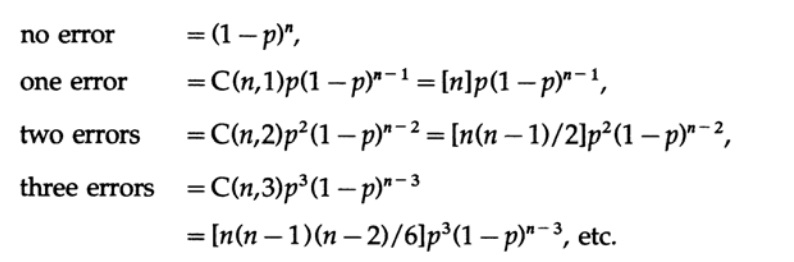
したがって、通常のように、ブロックnの長さに対してpが小さい（積npが小さいことを意味する）場合、複数のエラーは単一のエラーよりもはるかに少なくなります。 所定の確率pに対する長さnの選択は、工学的な解決策です。 nが小さい場合、nが大きい場合よりも冗長性（送信可能なビット数の最小ビット数に対する比n /（n-1））が大きくなりますが、npが大きい場合、冗長性は小さくなりますが、確率は高くなりますエラーを検出しません。 これら2つの効果のバランスをとる方法について、工学的な決定を下す必要があります。

単一のエラーが見つかった場合は、メッセージの再送信を要求して、正しい結果を2回、または3回など待機することができます。 ただし、保存されたメッセージが正しくない場合は、別のエラーが表示されるまで再送信を要求し、単一のエラー検出スキームで2つの未検出エラーが発生する場合があります。 したがって、再送信は予想されるエラーの性質に依存する必要があります。



このようなコードは、リレーの時代でも広く使用されていました。 電話会社は、セントラルオフィスと初期のリレーマシンで2-out-5コードを使用しました。つまり、5つのリレーのうち2つだけが「オン」の位置にありました。 C（5、2）= 10であるため、このようなコードは10進数を表すために使用されました。 正確に2つのリレーが「オン」位置にない場合、これはエラーを意味し、繰り返しがありました。 また、3-of-7コード、明らかに奇妙なチェックコードもありました。



Bell LabsでModel 5リレーコンピューターを使用するときにこれらの2 of 5コードに初めて精通し、正しい答えを得るための支援に感銘を受けただけでなく、もっと重要なことには、技術スタッフに機会を与えました実際にマシンにサービスを提供します。 ほぼすべてのエラーは、コミッション時にマシンによって検出されたため、ノーズで操作するのではなく、技術担当者に正しい方向を示し、誤動作を見つけるために正しく機能する部品の設定を強制的に変更しました。



物語の時系列に違反しているが、イデオロギー的であり、AT＆Tはかつて人々が26文字のアルファベット、10桁の10進数、およびスペースを使用した場合のコーディングの使用方法を尋ねました。 これは、インベントリの命名、部品の命名、および建物の命名を含む他の多くのアイテム名の典型です。 ダイヤルエラーに関するデータとプログラミングの長年の経験から、人々は隣接する数字を再配置する顕著な傾向があることを知っていました：67は76になり、孤立した数字を交換します（通常、数字を2倍にすると556は566になります） 。 したがって、単一エラーの検出だけでは不十分です。 私は2人の非常に有能な人を会議室に連れて行き、彼らに質問をしました。 最終的にそのうちの1人であるEd Gilbertが重み付きコードを提案するまで、申し出を拒否しました。 特に、彼は数字0、1、2、... 36で記号0、1、... 9、A、B、...、Z、スペースを示すことを提案しました。 その後、彼は値の合計を計算しませんでしたが、n番目の文字に値（便宜上マーク）Skがあったかどうか、次にn文字のメッセージに対して計算します







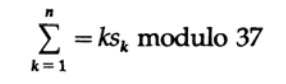
ここでの「モジュロ」とは、加重合計が37で除算され、除算の残りだけが使用されることを意味します。 メッセージをn文字でエンコードするには、最初の文字k = 1を空のままにし、37より小さい剰余の値に関係なく、37から減算し、対応する文字を使用してチェックします。これは最初の位置に配置する必要があります。 したがって、最初の位置に検証文字を含むメッセージ全体のテストサムは0になります。2つの異なる文字を並べ替えたり、単一の文字を置き換えることを検討すると、37を法とする重み付きパリティが壊れます（置き換えられた場合に限ります）文字は37文字離れていません）。 詳細を説明しませんが、モジュールが37である素数であることが重要であることに注意してください。



必要に応じて、シンボルの重み付き合計（実際にはそれらの値）を取得するには、積を回避して加算と減算のみを使用できます。 列内の文字を順番に並べ、小計を計算し、小計の小計を37を法として計算し、これを37に加算すると、チェックディジットが得られます。 例として、w、x、y、zを使用します。







受信側では、a-0（正しい文字）またはaが負の数（間違った文字）になるまでモジュールを再減算します。



たとえば、インベントリに名前を付けるためにこのエンコードを使用する必要がある場合、転送中に間違った名前が最初に表示された場合、それより前ではない場合（おそらく予備プロセスで）、エラーが検出されるので、注文するまで待つ必要はありません後でそのような名前がないという回答を受け取るため、または間違った注文を受け取るために、本社に配信されます。 エラーは注文が出される前に検出されるため、簡単に修正できます。 ただ？ はい！ （ホワイトノイズの例とは対照的に）人為的エラーに対して効果的です。



実際、今日、ISBN番号のある本で同様のコードを見ることができます。 これは同じコードで、10桁の10桁のみを使用し、10という数字は素数ではないため、Xの11番目の文字を入力する必要がありました。これはパリティチェック中に時々表示されることがあります。パリティ用のISBNの最後の文字としてXを使用します。 ダッシュは主に装飾的な機能を果たし、コーディングには使用されません。 教科書で自分で確認してください。 他の多くの大規模な組織は、努力をしたい場合、そのようなコードを良い効果のために使用できます。



繰り返しますが、将来的には記号の形の情報が重要になり、物質的なものはそれほど重要ではなくなると考えているため、便利なコードで情報をコーディング（表現）する理論は重要なトピックです。 上記の資料は、マシンの単純なエラー検出コードと、人間が使用する重み付きコードを提供します。 これらは、機械エラーと人的エラーが発生する可能性がある状況でコーディング理論がどのように役立つかを示す2つの例にすぎません。



人間とコンピューターのインターフェースについて考えるとき、役立つと思うことの1つは、人がキーストロークをできる限り少なくする必要があることです-ハフマンコーディングアンダーカバー！ プログラムメニューのさまざまなブランチの確率を考えると、必要に応じて、キーストロークの総数を減らす方法を思いつくことができます。 したがって、すべての人に同じインターフェースを提供する代わりに、同じメニューのセットを異なる人々の習慣に合わせてカスタマイズできます。 広義には、高レベル言語の「自動プログラミング」は、ハフマンコーディングのようなものを達成するための試みであり、比較的少数のキーストロークを使用して目的の問題を解決し、他のキーを使用する他のタスクを実行します。



継続するには...



誰が本の翻訳、レイアウト、出版を手伝いたいのか-個人のメールまたはメールで書くmagisterludi2016@yandex.ru



ちなみに、私たちはまた別のクールな本の翻訳を開始しました- 「The Dream Machine：The History of the Computer Revolution」 ）