これは勾配降下の本質ですが、多次元空間に移動すると、たとえその実際のジオメトリがほとんどわからない場合、類推は常にばらばらになります。 これは通常、問題にはなりませんが、勾配降下は非常にうまく機能するようです。
しかし、ここで重要な質問があります。実際の地球上で勾配降下はどれだけうまく実行されているのでしょうか?
重みとコスト関数の定義
一般モデルでは、勾配降下法により、コスト関数を最小化するモデルの重みが選択されます。 これは通常、多くの予測に対してモデルによって作成されたエラーの表現です。 しかし、ここでは何も予測しないため、「間違い」はありません。したがって、地球上を旅行するためには、通常の機械学習のコンテキストを少し拡張する必要があります。
地球旅行アルゴリズムの目標は、あらゆる開始位置から海面に到達することです。 つまり、緯度と経度として「重み」を定義し、現在の高度として「コスト関数」を定義します。 言い換えれば、勾配降下は、高度を最小化するような方法で緯度と経度の値を最適化する必要があります。 残念ながら、地球全体の表面に対する数学関数はないため、NASAラスタデータセットからコスト値を計算します。
import rasterio # Open the elevation dataset src = rasterio.open(sys.argv[1]) band = src.read(1) # Fetch the elevation def get_elevation(lat, lon): vals = src.index(lon, lat) return band[vals] # Calculate our 'cost function' def compute_cost(theta): lat, lon = theta[0], theta[1] J = get_elevation(lat, lon) return J
勾配降下では、最適化が実行される各変数に関するコスト関数の勾配が考慮されます。 彼は変数がコスト関数を減らすように調整します。 これは、コスト関数が二乗平均平方根誤差などの数学的メトリックである場合は簡単です。 しかし、すでに述べたように、「コスト関数」はデータベース内の検索であるため、派生するものは何もありません。

幸いなことに、私たちの例えで旅行者と同じ方法で勾配を概算できます。 勾配は勾配に相当するため、現在の位置よりわずかに高い点とそれよりわずかに低い点(各次元)を取得して勾配を推定し、それらを除算して推定導関数を取得します。 このオプションは非常にうまく機能するはずです。
def gradient_descent(theta, alpha, gamma, num_iters): J_history = np.zeros(shape=(num_iters, 3)) velocity = [ 0, 0 ] for i in range(num_iters): cost = compute_cost(theta) # Fetch elevations at offsets in each dimension elev1 = get_elevation(theta[0] + 0.001, theta[1]) elev2 = get_elevation(theta[0] - 0.001, theta[1]) elev3 = get_elevation(theta[0], theta[1] + 0.001) elev4 = get_elevation(theta[0], theta[1] - 0.001) J_history[i] = [ cost, theta[0], theta[1] ] if cost <= 0: return theta, J_history # Calculate slope lat_slope = elev1 / elev2 - 1 lon_slope = elev3 / elev4 - 1 # Update variables theta[0][0] = theta[0][0] - lat_slope theta[1][0] = theta[1][0] - lon_slope return theta, J_history
いいね! この関数は、変数XまたはYが渡されないという点で、ほとんどの勾配降下の実装とは異なります。コスト関数では、予測の誤差を計算する必要がないため、ここで最適化する変数のみが必要です。 ワシントンのオリンパス山で実行してみましょう。
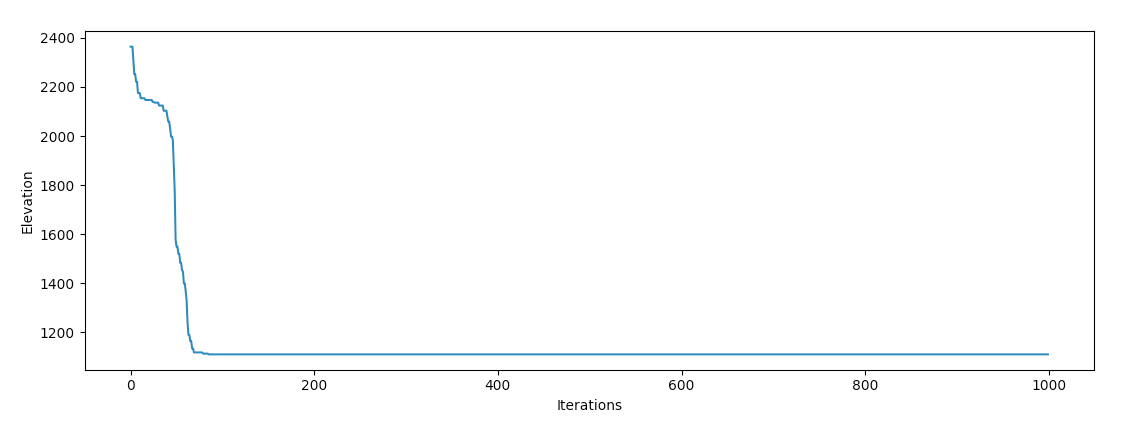
うーん、彼が立ち往生しているように見えます! 他のほとんどの場所でテストする場合も同じことが起こります。 地球は極小値であふれており、勾配降下は、海の近くでさえもローカルエリアから打ち上げられた場合、グローバルミニマムを見つけるのが非常に困難です。
慣性最適化
標準の勾配降下が唯一のツールではないため、慣性による最適化(運動量の最適化)を試してください。 慣性は実際の物理学に基づいているため、実際のジオメトリの勾配降下に適用することは魅力的なアイデアです。 残念ながら、オリンパスの上に非常に大きな岩を置いて手放すと、海洋に到達するための慣性を持つ可能性は低いため、いくつかの非現実的な(物理的な意味での)ガンマ値を使用する必要があります。
def gradient_descent(theta, alpha, gamma, num_iters): J_history = np.zeros(shape=(num_iters, 3)) velocity = [ 0, 0 ] for i in range(num_iters): cost = compute_cost(theta) # Fetch elevations at offsets in each dimension elev1 = get_elevation(theta[0] + 0.001, theta[1]) elev2 = get_elevation(theta[0] - 0.001, theta[1]) elev3 = get_elevation(theta[0], theta[1] + 0.001) elev4 = get_elevation(theta[0], theta[1] - 0.001) J_history[i] = [ cost, theta[0], theta[1] ] if cost <= 0: return theta, J_history # Calculate slope lat_slope = elev1 / elev2 - 1 lon_slope = elev3 / elev4 - 1 # Calculate update with momentum velocity[0] = gamma * velocity[0] + alpha * lat_slope velocity[1] = gamma * velocity[1] + alpha * lon_slope # Update variables theta[0][0] = theta[0][0] - velocity[0] theta[1][0] = theta[1][0] - velocity[1] return theta, J_history
変数を少し調整した後、勾配降下により海を見つける可能性が高くなります。
成功! オプティマイザーの動作を観察することは興味深いです。 降下中に彼は谷に落ち、一方から他方に「転がった」ようです。これは、非常に慣性の大きい物体が現実の世界でどのように振る舞うべきかという私たちの直感と一致しています。
最終的な考え
現実には、地球は最適化が非常に簡単な機能でなければなりません。 主に海洋で覆われているため、この関数の可能な入力値の3分の2以上がコスト関数の最適値を返します。 しかし、私たちの惑星は、極小と非凸地に悩まされています。
このため、機械学習の最適化手法が具体的で理解可能なローカルジオメトリでどのように機能するかを研究するための多くの興味深い機会を提供すると思います。 彼らはオリンパスで良い仕事をしたようですので、勾配降下「確認」を説明するために通常のアナロジーを検討します!
これについて考えがあれば、 Twitterで私に知らせてください!
プロジェクトコードはこちらです。