最初の観察では、2×2テクスチャの対角線でサンプリングすると、出力は2次ベジエ曲線上の点になり、曲線上の参照点は下の画像のようにピクセル値になります。 二次ベジエ曲線を取得すると言うとき、文字通り正確に自分自身を表現します。 これは、次のように表すことができます。テクスチャ補間は、文字通りde Casteljoアルゴリズムを実行します。 (注:下の例で「B」の値が等しくない場合、2番目の基準点はこれら2つの値の中間になります。拡張機能は、より多くの曲線をより少ないピクセルに近づけるためにこれを悪用します)。

私の計画は、対角線45°以外の方向でピクセルをサンプリングするときに何が起こるかを見ることでした。 特に、次のことが重要です。
- 別の回線を試すとどうなりますか?
- たとえば、2次曲線に沿ってサンプリングした場合、 ?
- 円または正弦波を試すとどうなりますか?
- トライリニアまたはクアドリリニア補間のように、サンプルパターンは高次元でどのように変化しますか?
最初の質問の答えに偶然出会ったとき、他の人を見る時が来ました!
P. S.これの用途は何ですか? 頭に浮かぶ最高のものは、GPUでのデータ圧縮です。 区分的有理多項式で近似される場合、このメソッドのアイデアは、GPUで迅速かつ簡単にデコードされるデータ(テクスチャ内のピクセル)の圧縮に役立ちます。 この記事のアイデアにより、区分的有理多項式を除き、データの近似と保存に他のタイプの曲線を使用できます。 さらに、曲線と高次のサーフェスは、より少ないテクスチャを使用します。
クイックセットアップ:バイリニア補間式
バイリニア補間は、サブピクセルの詳細を取得する方法として、最新のGPUで利用できます。 昔、テクスチャをスケーリングするとき、最も近い隣接ポイントに補間が使用されていたため、正方形のピクセルが単純に増加しました。 現在、バイリニア補間は、最も近い隣接点での補間よりもピクセル間のスペースを埋めます。
バイリニア補間は、x軸に沿って2つの値を補間し、y軸に沿って(または逆に)結果を補間することで説明できます。 数学的には、次のようになります。
ここで、xとyは、ピクセル間のポイントの位置を表す0〜1の値であり、A、B、C、Dは、計算するポイントの周囲に長方形を形成する4つの最も近いピクセルの値です。 A =(0,0)、B =(1,0)、C =(0,1)、D =(1,1)。
いくつかの変換後、この式はべき級数の形で提示され、実験に適しています。
双線形補間の詳細については、次のマテリアルを調べてください: 1、2、3、4 。
手元にある式で開始できます!
他の行での選択
したがって、サンプルがAからDに対角線方向に進むと、2次方程式が得られることがわかります。 他の回線ではどうなりますか?
答えを知る前に、45°の角度の線が2次方程式(次数2)を与え、水平線と垂直線が線形方程式(次数1)を与える場合、他の線に沿ったサンプルは1から2の間の次数を持つ多項式であると仮定しました答えは異なることが判明しましたが、1〜2の次数を持つ多項式の形式で「本当の答え」を解釈できるかどうかに興味がありました。
いずれにせよ、 ウィキペディアは私に促しました:
「内挿は、xまたはyに平行な線に沿って線形です。つまり、xまたはyが定数の場合です。 他の直線に沿った内挿は2次です。」
これは、水平線または垂直線が線形方程式になることを意味します。 他の行は2次を与えます。
見てみましょう。
線形関数の方程式は 文字通り置き換える に そして何が起こるかを見てください。
したがって、双線形補間の多項式のべき級数から始めます。
交換後、次のことが判明しました。
いくつかの拡張と単純化の後、次のものが得られます。
この式は、双線形補間A、B、C、Dの値(つまり、これらの点で囲まれた双線形表面)を報告し、次の式で定義されるx、y線に沿ってサンプリングします。 。
これは非常に一般化された関数であり、多くのことを話すのは困難ですが、1つはっきりしているのは、2次関数です! A、B、C、D、m、およびbに選択する定数値に関係なく、2次多項式(またはより低い次数ですが、決して高くなることはありません)を取得します。
このシェーダーは、ランダムなRGBテクスチャ(ホワイトノイズ)上のランダムなサブピクセルラインセグメントによって生成された曲線を示します。
(曲線の不均一なエッジは、補間が固定小数点形式X.8で行われるという事実によるものであるため、精度はかなり制限されていることに注意してください。この問題を解決するための詳細と方法については、上記の科学研究を参照してください)。

先に進みましょう そして さまざまな種類の回線で何が起こるかを確認します。
m = 0、b = 0
mとbが0の場合はどうなります。つまり、ラインに沿ってサンプリングするとどうなりますか 。
これらの値を代入すると、次が得られます。
興味深いことに、これはAとBの間の単なる線形補間であり、バイリニアサーフェス上のサンプルでグラフを見るときに意味があります。
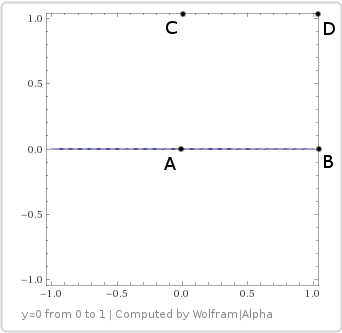
これは、ウィキペディアが私たちに言ったことと一致しています:座標の1つが変更されていない場合(水平線または垂直線)、結果は線形です。
m = 1、b = 0
m = 1とb = 0を試してみましょう。これが行です 。 グラフは、サンプルがバイリニアサーフェス上のどこから来たかを示しています。
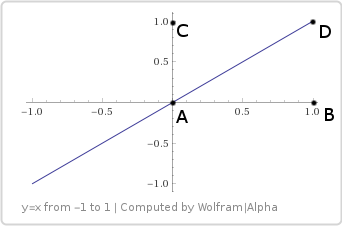
これらの値を代入すると、次の式が得られます。
二次方程式が得られましたが、これは驚くべきことではありません。 また、制御点を持つ二次ベジェ曲線の式でもあります 、 、 。
m = 2、b = 1
ラインを試してみましょう 双線形面でサンプリングするグラフを次に示します。
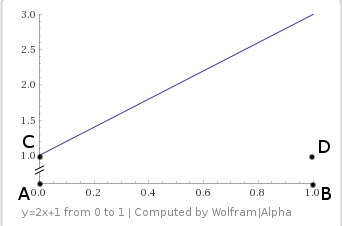
値を代入すると、次の方程式が得られます。
再び、二次関数が取得されます。
方程式が終わることに驚くかもしれません の代わりに しかし、チャートを見れば、それは理にかなっています。 xがゼロの場合、行は文字通りポイントCから始まります。
x = 2u、y = 3u
上記の例では、変数yをxの関数としてのみ変更します。 変数xも変更するとどうなりますか?
1つのオプションは、3番目の変数を入力することです 、0〜1の値を取ります。この変数を使用して、xとyを表現できます。
これら2つの方程式を使用するとどうなるか見てみましょう。
サンプルは、バイリニアサーフェス上のこのような線に沿って実行されます。

関数uをxとyに代入すると、次のようになります。
これはまだ二次方程式です!
二次軌道はどうですか?
したがって、バイリニアサーフェス上で直線で移動する場合、直線が水平または垂直の場合を除き、2次関数が取得されることがわかりました。 注:バイリニアサーフェスが平面の場合、このサーフェス上のすべての線は線形関数になるため、これは線形結果を得る別の方法です。 また、ポイントまで縮退することもできます。 直線で移動する場合、3次(またはそれ以上)の結果は得られません。
直線に沿って選択する代わりに、2次曲線などの他の形状が選択された場合はどうなりますか?
y = x * x
関数から始めましょう 。 結果の曲線は次のとおりです。
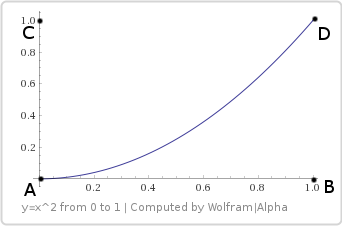
べき級数形式の双線形補間の形式に戻って、置き換えましょう の代わりに そして何が起こるかを見てください。
初期方程式は次のとおりです。
このようになります:
それは変わります:
これは三次方程式です!
ランダムなピクセルに対してこの軌跡を描くシェーダーは次のとおりです。

この例の確かな優雅さは、3次方程式が4つの参照点に基づいた4つの係数を持っているため、いわば「すべてが成り立つ」ということです。
これは、3つのアンカーポイントが4つのピクセル値に格納されている線形セグメントに沿ったサンプリングとは異なります。 この場合、そのうちの1つは少し冗長です。
この事実を使用できますが、2次パスに沿ってサンプリングして3次曲線を取得するのは自然な近似のようです。
x = u * u、y = u * u
xとyに沿って二次的に移動するとどうなるか見てみましょう。
線形の場合と同様に、3番目の変数uがあり、0から1まで変化し、この変数に基づいてxとyがあります。 次の方程式を使用します。
サンプリングパスは次のとおりです。
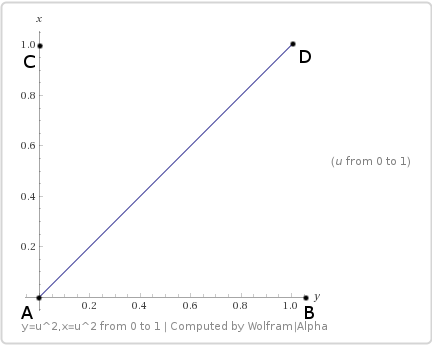
値を代入すると、4次の方程式が得られます。
直線的なパスを見て驚くかもしれません。 グラフ内で非線形に変化する場合でも、xは常にyと等しいというだけです: シェーダー 。

高次曲線:x = 3u ^ 2、y = 2u ^ 4
これらの方程式をとって、少しはしゃぎましょう。
そのようなサンプリングパスに対応するもの:
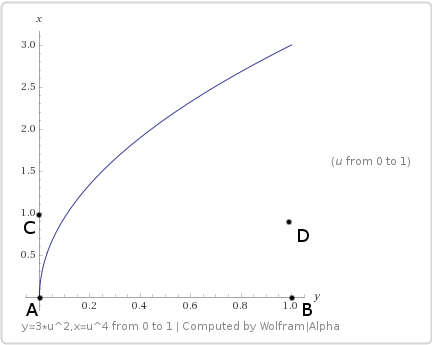
値を代入すると、双線形補間方程式...
...は6次の方程式になります。
Shadertoyシェーダージェネレーターは通常どおりランダムピクセルでレンダリングしますが、uが0から1に変わると、xが0から3に変わり(yは0から1の範囲内にあります)、ピクセルの境界に明らかなギャップが生じます。 純粋に数学的な定式化では、このようなものはありませんが、実際のテクスチャでサンプリングするため、安全な家(0,1)を離れると、他の基準点を持つ完全に新しい領域にいます 。

三角関数:y = sin(2 * pi * x)
機能を試してみましょう 双線形表面上のそのような経路をたどる:
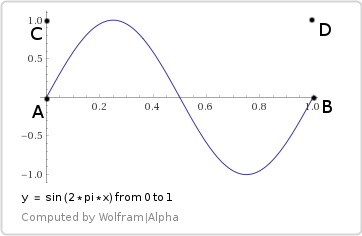
双線形補間方程式は三角多項式になります:
元のピクセル領域を超えるためにギャップがあるため、この場合、 このシェーダーは 。 0から1の間になるようにy値をスケーリングおよびシフトします。

円周
最後に、循環サンプリング。
その軌跡は次のとおりです。
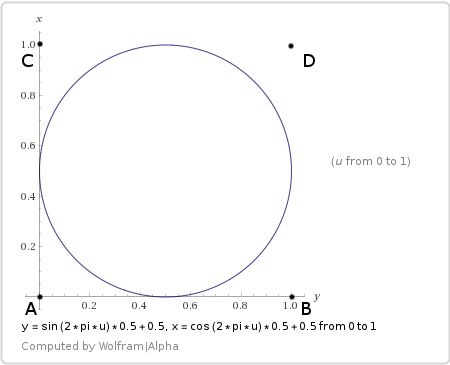
双一次方程式を代入します。
シェーダーのマッチング 。
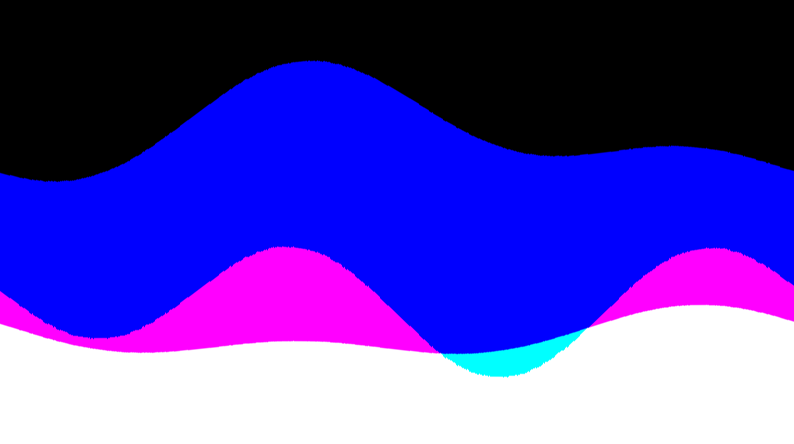
円の中のサンプルの顕著な特徴は、その連続性です。 曲線の左側が静かに右側に移動していることに注目してください。 これは非常に便利な機能のようです。
進む
少し荒野に入りましたが、選択パスを慎重に選択すれば、ごく少数のピクセルでデータをエンコードおよびデコードする機会がたくさんあることを願っています。
これは、単純な対角線サンプリング法よりも複雑であり、シェーダー命令が必要です。 特に、シェーダーでは、リニアテクスチャを補間器に転送する前に、xまたはyの変更をエンコードする必要があります。 これは、メソッドがより多くのALUリソースを必要とすることを意味します。 しかし、彼はテクスチャメモリを節約します。
記事の冒頭にリストされているものからの最後の質問:サンプルパターンは、トリリニアまたはクアドリリニア補間などの高次元でどのように変化しますか?
さて、ここでのメカニズムは、双線形補間の場合とほぼ同じですが、測定値が増えるだけです。
2次元双一次補間では、xとyを関数に変換した後(相互または3番目の変数uから)、結果の多項式はxとyの累乗の合計に等しい次数を持つことがわかりました。
3次元補間による3次元では、結果の多項式の次数は、x、y、zの合計に等しくなります。
4次元補間を使用した4次元で、次数zを追加します。
カーブではなく、サーフェスまたは(ハイパー)ボリュームが必要な場合を考えてください。
サーフェスとボリュームで機能する拡張機能で見たように、次数Nの多項式がある場合、各軸の次数の合計がNに追加されると、多次元多項式(サーフェスまたはハイパーボリュームとも呼ばれます)に分割できます。
これは、私たちが今話したことについてであり、まさに反対です。
将来勉強するのに面白いと思うものがあります-行き過ぎるとどんな制限が生じるかを見るために。
たとえば、UV座標の任意のラインに沿ってサンプリングすると、2×2テクスチャは2次関数を与えることができます。 最初に座標uを3次関数で表現し、座標vを別の3次関数で表現すると、バイキュービックサーフェスを作成できると思います。
サーフェスは、一般的なバイキュービックサーフェスの可能な形状のサブセットに制限されますが、実際にはバイキュービックサーフェスを取得します(基本的に、ピクセルを追加し、より高い次元の追加選択または線形補間を行わない限り、制御しない暗黙のアンカーポイントがあります)。
どんな制限があり、そのようなものから本当の利益を得る機会があるかどうかを見たいです。
とにかく、読んでくれてありがとう! アイデア、修正、ユースケース-投げて!
@ Atrix256