はじめに
状態変数を使用した時間領域での制御システムの研究は、分析の単純さのために最近広く使用されています。
システムの状態は、特定のユークリッド空間内のポイントに対応し、時間内のシステムの動作は、このポイントによって記述される軌道によって特徴付けられます。
この場合、数学的装置には、アナログおよび離散LQRおよびDLQRコントローラー、カルマンフィルター、およびこれらすべてを行列とベクトルを使用した既製のソリューションが含まれます。
この出版物の目的は、Pythonソフトウェアを使用して状態空間を記述することにより、最適な制御システムを設計する問題の解決を検討することです。
簡単に理論
測定方程式を考慮した線形動的オブジェクトモデルのベクトル行列記録は、次の形式を取ります。
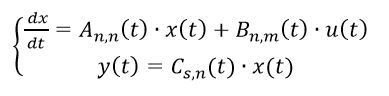（1）
行列A（t）、B（t）、C（t）が時間に依存しない場合、オブジェクトは定数係数を持つオブジェクト、または静止オブジェクトと呼ばれます。 そうしないと、オブジェクトは不安定になります。
測定に誤差がある場合、出力（調整可能）信号は線形化された行列方程式によって設定されます。
（2）
ここで、y（t）は調整可能な（測定された）量のベクトルです。 C（t）は、測定ベクトルと状態ベクトルの関係の行列です。 v（t）は、測定誤差（干渉）のベクトルです。
方程式（1）および（2）を実装する線形連続システムの構造を図に示します。
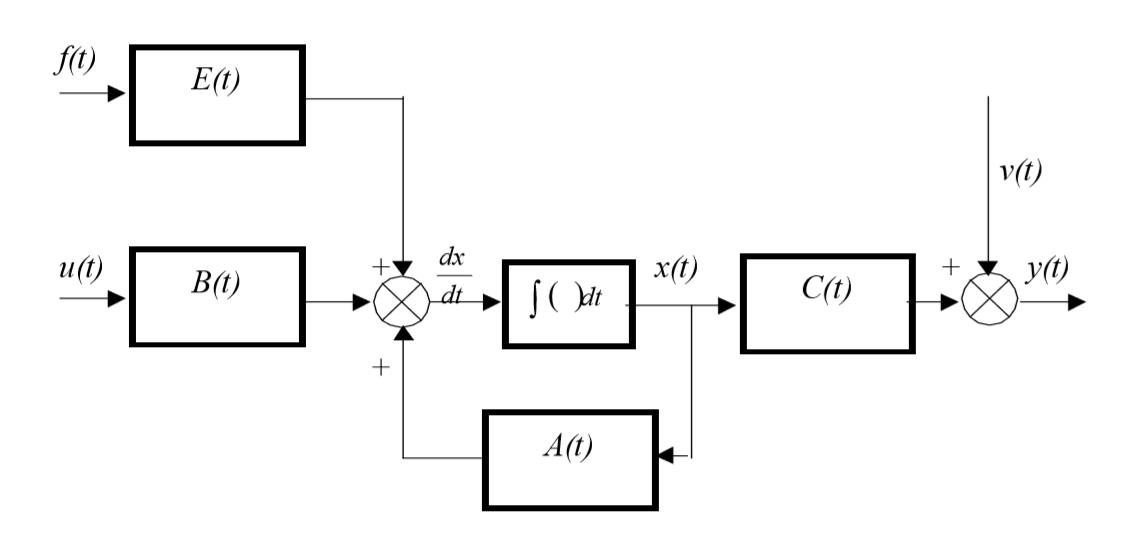
この構造は、入力x（t）、u（t）、出力y（t）、内部、または位相座標x（t）の状態空間で構築されたオブジェクトの数学モデルに対応します。
たとえば、永久磁石から独立して励起されるDCモーターの数学モデルを考えます。 検討中のケースのエンジンの電気および機械部品の方程式系は次のようになります。
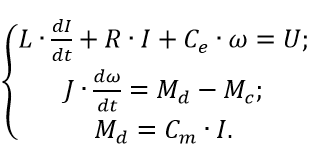（3）
最初の方程式はアンカーチェーンの変数間の関係を反映し、2番目の方程式は機械的平衡の条件を反映します。 一般化された座標として、電機子電流Iと電機子の回転周波数ωを選択します。
制御は電機子Uの電圧、外乱は負荷抵抗モーメントMcです。 モデルパラメータは、回路と電機子のアクティブ抵抗とインダクタンスであり、それぞれRとで示され、慣性モーメントJと構造定数ceとcm（SIシステムではCe = Sm ）が減少しています。
元のシステムを一次導関数と比較して解くと、状態空間でエンジンの方程式が得られます。
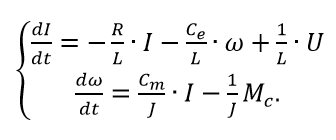（4）
行列形式では、方程式（4）は（1）の形式を取ります。
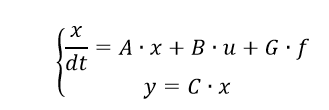（5）
は、一般化された座標のベクトルです
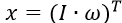、制御ベクトルU = u （検討中の場合、スカラー）、摂動Mc = fのベクトル（スカラー）。 マトリックスモデル：
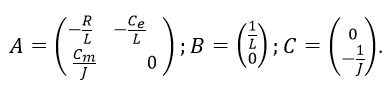（6）
回転周波数が調整可能な量として選択されている場合、測定式は次の形式で記述されます。
（7）
測定マトリックスは次の形式を取ります。
C =（0 1）
Pythonでエンジンモデルを作成しましょう。 これを行うには、最初にエンジンパラメーターの特定の値を設定します。U= 110 V; R = 0.2オーム; L = 0.006 H; J = 0.1 kg / m2; Ce = Cm = 1.3 V / Cそして、（6）からオブジェクトの行列係数によって値を見つけます。
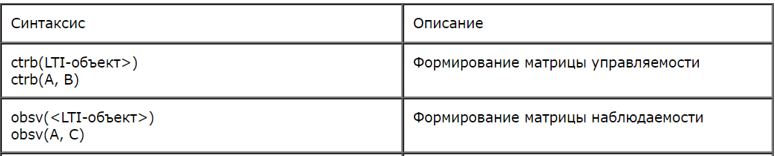
可観測性と可制御性のためのマトリックステストでエンジンモデルを形成するプログラムの開発：
プログラムの開発時に、特別な関数def matrix_rankを使用して、マトリックスのランクと表に示す関数を決定しました。
# -*- coding: utf8 -*- from numpy import* from control.matlab import * from numpy.linalg import svd from numpy import sum,where import matplotlib.pyplot as plt def matrix_rank(a, tol=1e-8): s = svd(a, compute_uv=0) return sum( where( s>tol, 1, 0) ) u=110 # J=.1 # c=1.3; # R=.2; L=.006 # A=matrix([[-R/L ,-c/L],[ c/J ,0]]) print (' : \n %s'%A) B=matrix([[1/L],[0]]) print (' B : \n %s '%B) C=matrix([[0, 1]]) print (' C : \n %s '%C) D=0 print (' D : \n %s '%D) sd=ss(A,B,C,D) # wd=tf(sd) # print (' : \n %s '%wd) a=ctrb(A,B) print(' : %s'%matrix_rank(a, tol=1e-8)) a=obsv(A,C) print(' : %s'%matrix_rank(a, tol=1e-8)) y,x=step(wd) # plt.plot(x,y,"b") plt.title(' ') plt.ylabel(' /') plt.xlabel(' ') plt.grid(True) plt.show()
プログラムの結果：
マトリックスA：
[[-33.33333333 -216.66666667]
[13. 0.]]
マトリックスB：
[[166.66666667]
[0.]]
マトリックスC：
[[0 1]]
スカラーD：
0
エンジン伝達関数：
2167 /（s ^ 2 + 33.33 s + 2817）
管理性マトリックスのランク：2
可観測性行列ランク：2
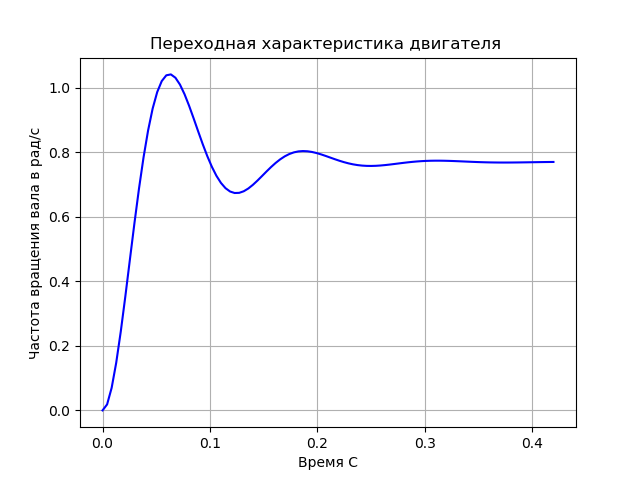
結論：
1.独立した磁気励起を備えた直流モーターの例を使用して、状態空間における制御設計手法を検討します。
2.プログラムの結果として、伝達関数、遷移特性、および可制御性行列と可観測性行列のランクが取得されます。 ランクは状態空間の次元と一致し、モデルの制御性と可観測性を確認します。
離散dlqrコントローラーと完全なフィードバックを使用して最適な制御システムを設計する例
定義と用語
線形二次レギュレータ（LQR）-制御理論において、二次品質関数を使用する最適なレギュレータのタイプの1つ。
システムが線形微分方程式で記述され、品質インジケーターが2次関数であるタスクは、線形2次制御問題と呼ばれます。
線形2次コントローラー（LQR）および線形2次ガウスコントローラー（LQG）が広く使用されています。
問題の実用的な解決策を開始するときは、常に制限を覚えておく必要があります
線形定常システムの最適な離散コントローラーを合成するには、ベルマン方程式を数値的に解く関数が必要です。PythonControl Systemsライブラリ[1]にはそのような関数はありませんが、[2]で与えられるリカッチ方程式を解く関数を使用できます：
def dlqr(A,B,Q,R): """Solve the discrete time lqr controller. x[k+1] = A x[k] + B u[k] cost = sum x[k].T*Q*x[k] + u[k].T*R*u[k] """ #ref Bertsekas, p.151 #first, try to solve the ricatti equation X = np.matrix(scipy.linalg.solve_discrete_are(A, B, Q, R)) #compute the LQR gain K = np.matrix(scipy.linalg.inv(BT*X*B+R)*(BT*X*A)) eigVals, eigVecs = scipy.linalg.eig(AB*K) return K, X, eigVals
ただし、[3]に記載されている最適なコントローラーの合成に関する制限も考慮する必要があります。
- マトリックス（A、B）で定義されるシステムは安定化可能でなければなりません。
- 不等式S> 0、Q-N / R – NT> 0、1組の行列（Q-N / R – NT、
A-B / R-BT）固有値がオンの観測可能なモードを使用しないでください
実軸。
明確で理由は分からないが、広範で曖昧な理論を掘り下げた後、問題は解決し、すべての答えはコードへのコメントで直接読むことができます。
すべての状態変数に関するフィードバックを備えた制御システムのコントローラーのブロック図を図に示します。
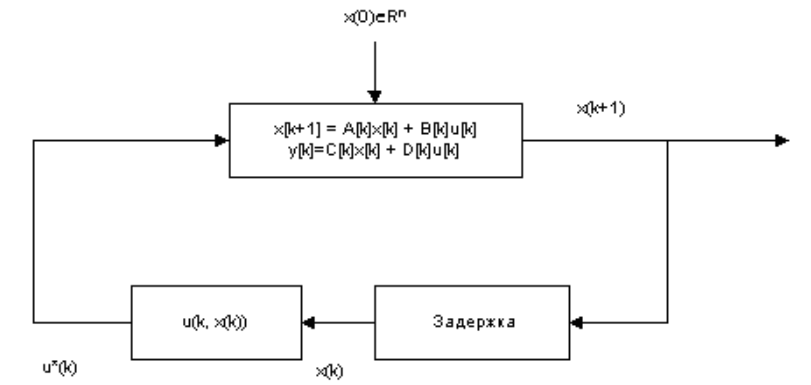
初期状態x0ごとに、最適な線形コントローラーは最適なプログラム制御u *（x、k）と最適な軌道x *（k）を生成します。
dlqrコントローラーで最適な制御モデルを形成するプログラム
from numpy import * import scipy.linalg import matplotlib.pyplot as plt def dlqr(A,B,Q,R): # x[k+1] = A x[k] + B u[k] P= matrix(scipy.linalg.solve_discrete_are(A, B, Q, R)) # DLQR K = matrix(scipy.linalg.inv(BT*P*B+R)*(BT*P*A)) E, E1 = scipy.linalg.eig(AB*K) return K, P, E """ """ A=matrix([[1, 0],[ -2 ,1]]) B=matrix([[1, 0],[1, 0]]).T """ """ Q=matrix([[0.5, 0],[0, 0.5]]) R=matrix([[0.5,0],[0, 0.5]]) T =100# SS=0.5# N =int(T/SS)# K, P, E=dlqr(A,B,Q,R)# print("K= \n%s"%K) print("P= \n%s"%P) print("E= \n%s"%E) x = zeros([2, N]) u= zeros([2, N-1]) x [0,0]=2 x [1,0]=1 for i in arange(0,N-2): u[:, i]= dot(- K,x[:, i]) x[:, i+1]=dot(A,x[:, i])+dot(B,u[:, i]) x1= x[0,:] x2= x[1,:] t = arange(0,T,SS) t1=arange(0.5,T,SS) plt.subplot(221) plt.plot(t, x1, 'b') plt.grid(True) plt.subplot(222) plt.plot(t, x2, 'g') plt.grid(True) plt.subplot(223) plt.plot(t1, u[0,:], 'y') plt.grid(True) plt.subplot(224) plt.plot(t1, u[1,:], 'r') plt.grid(True) plt.show()
計算結果：
K =
[[0.82287566 -0.17712434]
[0.82287566 -0.17712434]]
P =
[[3.73431348 -1.41143783]
[-1.41143783 1.16143783]]
E =
[0.17712434 + 0.17712434j 0.17712434-0.17712434j]
状態と制御のダイナミクス：x1、x2、u1、u2。
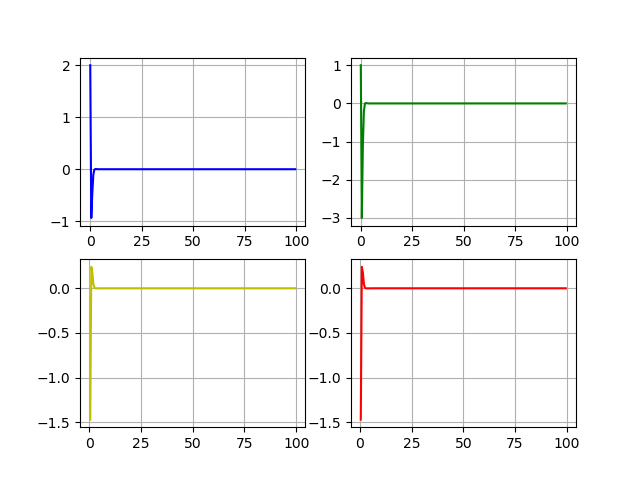
おわりに
説明したように、個別の最適制御問題は、Pythonを使用して解決できます.Python Control Systems、SciPy、NumPyライブラリの機能を組み合わせることで、もちろん、以前はこうした問題は有料の数学パッケージでしか解決できなかったため、Pythonの普及に貢献しています。