
はじめに
多くの場合、長い飛行距離を確保するために、追加のタンクが航空機の外側から吊り下げられます。 ぶら下がっているタンクは捨てられますが、捨てられません。
燃料が消費された後にドロップされたサスペンションタンクは、吊り下げられている爆弾ラックのロックから航空機の爆弾と同じ方法でドロップされます。
吊り下げられたタンクからの電力は、これらのタンクからシャットオフまたは多方向バルブを介して一般的なエンジン燃料供給システムにパイプラインを含めることによって実行されます。
興味深い事実は、戦後のベトナムのジャングルで、アメリカの飛行機によって投棄された多くの燃料タンクを見つけ始めたことです。
農民は戦車を見て、2隻のボートを手に入れました。 このようなボートは錆びず、重量も軽く、空力的な形状のおかげで非常に簡単にrowぎます。

そのようなボートがあればいいのですが、同時に、戦車がぶら下がっている飛行機が私たちの上を飛んでほしくありません。
船外燃料タンクの空力抵抗(AC)
飛行モードとタンクの形状に応じて、空力抵抗の特定のコンポーネントが優先されます。 たとえば、高速の超音速で動く鈍い回転体の場合、抵抗は波のようになります。
低速で動く合理化されたボディの場合、摩擦抵抗と渦損失が優先されます。
流線型ボディの後端面で生じる希薄化は、ボディの速度とは反対の方向の合力の出現にもつながります。
空力抵抗Faは、無次元の空力抵抗係数Cxによって特徴付けられます。

ここで、ρは摂動されていない媒体の密度、vはこの媒体に対する物体の速度、Sは物体の特徴的な領域、Cxは無次元の抗力係数であり、通常は実験的に決定され、計算による単純な回転の形式です。
最小面積Sおよび係数Cxの基準に従った回転体からの船外燃料タンクのレイアウト
単純な物体の抗力係数(Cx)を計算し、その結果を出版物[1]に記載されている実験と比較する際にデータを使用します。

(燃料の大部分を保持するために)シリンダーを挟んでタンクの両端にある回転体の場合、体積
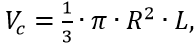 表面積
表面積  次のレイアウトオプションを選択できます。
次のレイアウトオプションを選択できます。
コーン(H = R)–ボリューム
 表面積
表面積 
コーン(H <> R)-ボリューム
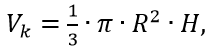 表面積
表面積 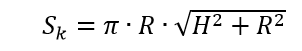
半球-ボリューム
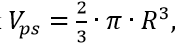 表面積
表面積 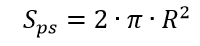


タンク容量を3 m3に設定します:Vb = Vps + Vc + Vk、Vb = 3、 最小Cx(2h = dまたはH = R)の条件が満たされない場合 、次のリストから最適なレイアウトの寸法を決定します。
# -*- coding: utf8 -*- import numpy as np from scipy.optimize import minimize import matplotlib.pyplot as plt def objective(x):# - x1=x[0]# R x2=x[1]# H , H=R x3=x[2]# L return 2*np.pi*x1**2+2*np.pi*x1*x3+np.pi*x1*((x1**2)+(x2**2))**0.5 def constraint(x): # return (2/3)*np.pi*(x[0]**3)+np.pi*x[2]*(x[0]**2)+(1/3)*x[1]*np.pi*(x[0]**2)-3 x0=[1,1,1]# b=(0.0,1)# bnds=(b,b,b) con={'type': 'ineq','fun':constraint} res = minimize(objective, x0,bounds=bnds,constraints=con) e=round(res['fun'],3) e1=round(res['x'][0],3) e2=round(res['x'][1],3) e3=round(res['x'][2],3) print (" :%s"%e) print (" :%s"%e1) print (" :%s"%e2) print (" :%s"%e3)
取得するもの:
推定吊りタンク面積:10.253
船外タンクの推定半径:0.878
推定船外タンクコーンの高さ:0.785
船外タンクシリンダーの推定長さ:0.393
所定のタンク容量Vb = 3 に対して、最小Cx(2h = dまたはH = R)の条件が満たされた場合、次のリストから最適なレイアウトの寸法を決定します。
# -*- coding: utf8 -*- import numpy as np from scipy.optimize import minimize import matplotlib.pyplot as plt def objective(x):# - x1=x[0] # R , H=R x2=x[1]# L return 2*np.pi*x1**2+2*np.pi*x1*x2+np.pi*x1*(2*(x1**2))**0.5 def constraint(x): # return (2/3)*np.pi*(x[0]**3)+np.pi*x[1]*(x[0]**2)+(1/3)*x[0]*np.pi*(x[0]**2)-3 x0=[1,1]# b=(0.0,1)# bnds=(b,b) con={'type': 'ineq','fun':constraint} res = minimize(objective, x0,bounds=bnds,constraints=con) e=round(res['fun'],3) e1=round(res['x'][0],3) e2=round(res['x'][1],3) print (" :%s"%e) print (" :%s"%e1) print (" :%s"%e1) print (" :%s"%e2)
取得するもの:
推定吊り下げタンク面積:10.259
船外タンクの推定半径:0.877
船外タンクの円錐の高さの推定値:0.877
シリンダー吊りタンクの長さの推定値:0.363
結論:
条件R = Hが満たされない場合のオプションと比較すると、タンクの総表面積はほとんど変化しません。 このレイアウトオプションは最適であり、実際に確認されています。
例として数値を示しますが、それぞれの場合、設計上の特徴を考慮する必要があります。
船外燃料タンクの燃料レベル測定
ジェットエンジンの動作は、タンク内のレベルに応じて調整される供給燃料の流量に依存します。 したがって、タンク内の燃料レベルを測定することは重要な技術的パラメーターです。
リセット不可能な燃料タンクでは、燃料レベルは直接チャンネルに設置されたセンサーによって測定されます。センサーの上部開放端は、ブースト圧力Poによりチャンネルを満たす燃料レベルの上にあります。
垂直チャネルと燃料タンクは通信する容器です。 タンク内の燃料レベルを下げると、チャンネル内の燃料レベルが下がります。 チャンネル内の燃料レベルがセンサーに達すると、センサーが作動します。 信号は燃料管理システムに入ります。
したがって、チャネル内の燃料レベルがタンク内の燃料レベルを決定します。 問題は、燃料と燃料タンクの自由表面が一致しないことです。 燃料レベルの測定エラーは、非効率的な燃料消費につながります。

タンク内の燃料レベルは、比率に従って変化します。

ここで、Hoはタンク内の初期燃料レベルです。 V –燃料供給率。 tは時間です。
燃料供給量の時間依存性のさらなる分析のために、出版物[2]で得られた関係を使用します:

ここで、yは測定チャネル内の燃料の自由表面の座標です。 L–円筒形の測定チャネルの壁に対する流体摩擦係数。 Rは、円筒形の測定チャネルの半径です。 gは重力加速度です。
微分方程式(1)の初期条件の形式は次のとおりです。
y(0)= Ho、dy / dt = 0
Pythonを使用して微分方程式(1)を数値的に解くために、次の表記法を導入します。

測定チャネルの平均燃料速度の変化。
# -*- coding: utf8 -*- import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt R=0.0195 H=8.2 g=9.8 L=4.83*10**-2 V=0.039 def f(y,t): y1,y2=y return [y2,-g+(g*(HV*t)/y1)+((L/(4*R))*y2**2)] t = np.arange(0,200,0.01) y0=[H,0] [y1,y2]=odeint(f,y0,t,full_output=False).T plt.title(" \n ") plt.xlabel("t,s") plt.ylabel("U,m/s ") plt.plot(t,y2) plt.grid(True) plt.show()
取得するもの:

測定チャネルおよびタンク内の燃料レベル。
# -*- coding: utf8 -*- import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt R=0.0195 H=8.2 g=9.8 L=4.83*10**-2 V=0.039 def f(y,t): y1,y2=y return [y2,-g+(g*(HV*t)/y1)+((L/(4*R))*y2**2)] t = np.arange(0,10,0.01) y0=[H,0] [y1,y2]=odeint(f,y0,t,full_output=False).T plt.title(' ') plt.ylabel('H,m') plt.ylabel('t,s') plt.plot(t,y1,"b",linewidth=2,label=' ') y=HV*t plt.plot(t,y,"--r",linewidth=2,label=' ') plt.grid(True) plt.legend(loc='best') plt.show()
取得するもの:

燃料レベルの測定エラー。
# -*- coding: utf8 -*- import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt R=0.0195 H=8.2 g=9.8 L=4.83*10**-2 V=0.039 def f(y,t): y1,y2=y return [y2,-g+(g*(HV*t)/y1)+((L/(4*R))*y2**2)] t = np.arange(0,200,0.01) y0=[H,0] [y1,y2]=odeint(f,y0,t,full_output=False).T plt.title(' ') plt.ylabel('d,m') plt.xlabel('t,s') d=y1-(HV*t) plt.plot(t,d) plt.grid(True) plt.show()
取得するもの:
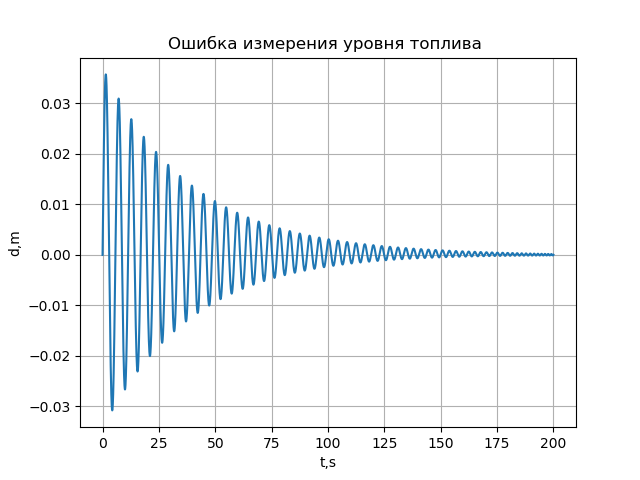
結論:
上記の数学モデルにより、航空機のタンク内の燃料レベルの測定における誤差を推定できます。
ロケットの場合、ロケットの燃料タンク内の液体の変動(変動)を考慮する必要があります。 このような変動は、出版物[3]に視覚的に示されています。
タンク内の燃料の変動を考慮するために、そのような単純化されたモデルを考慮することができます。
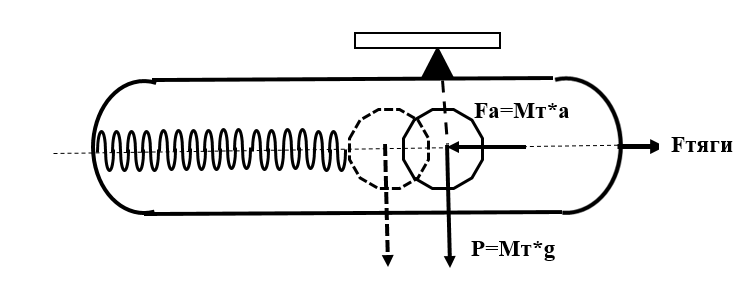
液体は、分散と剛性が低下した集中的に減少する質量と見なされます。 しかし、このトピックは別の記事です。
結論:
1.この記事では、船外燃料タンクの形状を最適化する例を使用して、いくつかの制限があるPythonの数値最適化機能を示します。
2.この記事では、非古典微分方程式を解く例を使用して、Pythonを使用してそのような方程式を解く可能性を示します。
3.得られたソリューションは、Mathcadまたは他の高価なパッケージの購入で学校や大学に負担をかけることなく、教育目的で使用できます。
参照: