TensorFlowを使用したヘシアンフリー最適化

こんにちは Hessian-FreeまたはTruncated Newton（Truncated Newton Method）として知られる最適化手法と、ディープラーニングライブラリTensorFlowを使用した実装についてお話したいと思います。 2次の最適化手法を利用しており、2次導関数の行列を読み取る必要はありません。 この記事では、HFアルゴリズム自体と、MNISTおよびXORデータセットでの直接配信ネットワークのトレーニングに関する作業について説明します。

---

最適化方法について少し

ニューラルネットワークを学習するには、その重みに関連して損失関数を最小化する必要があります。 したがって、この問題を解決するための多くの最適化方法があります。

勾配降下

勾配降下法は、微分可能な関数の最小値を連続して見つけるための最も簡単な方法です。 $$$f$ （ニューラルネットワークの場合、これは価値の関数です）。 いくつかのオプションがある $$$x$ （ネットワークの重み）およびそれらに関して関数を微分すると、偏導関数のベクトルまたは勾配ベクトルが得られます。

$$

$$\ nabla f（x）= \ langle \ frac {\ delta f} {\ delta x_1}、\ frac {\ delta f} {\ delta x_2}、...、\ frac {\ delta f} {\ delta x_n} \ラングル$$

勾配は常に関数の最大成長の方向を指します。 逆方向に移動した場合（つまり、 $$$-\ nabla f（x）$ ）その後、時間の経過とともに最小限になります。これが必要なことです。 最も単純な勾配降下アルゴリズム：

1. 初期化：オプションをランダムに選択 $$$x_0$
2. 勾配を計算します。 $$$\ nabla f（x_i）$
3. 負の勾配の方向にパラメーターを変更します。 $$$x_ {i + 1} = x_i-\ alpha \ nabla f（x_i）$ どこで $$$\ alpha$ -学習率のパラメーター
4. 勾配がゼロに近づくまで前の手順を繰り返します

勾配降下法はかなり単純で実績のある最適化手法ですが、マイナスもあります。これは一次であるため、コスト関数に関する一次導関数が使用されます。 これにより、いくつかの制限が課せられます。つまり、コスト関数は局所的に平面のように見え、その曲率は考慮されないことを意味します。

ニュートンの方法

しかし、コスト関数の2次導関数が提供する情報を取得して使用するとどうなりますか？ 二次導関数を使用した最もよく知られた最適化方法は、ニュートン法です。 この方法の主なアイデアは、コスト関数の2次近似を最小化することです。 これはどういう意味ですか？ それを理解しましょう。



一次元の場合を考えてみましょう。 関数があるとします： $$$f：\ mathbb {R} \から\ mathbb {R}$ 。 最小点を見つけるには、次のことがわかっているため、その導関数のゼロを見つける必要があります。 $$$f '（x）= 0$ 最低でも $$$f（x）$ 。 関数を近似する $$$f$ 2次のテイラー展開：

$$

$$f（x + \ delta）\約f（x）+ f '（x）\ delta + \ frac {1} {2} \ delta f' '（x）\ delta$$

探したい $$$\デルタ$ あれ $$$f（x + \ delta）$ 最小になります。 これを行うために、 $$$x$ そしてゼロに等しい：

$$

$$\ frac {d} {dx} \ bigg（f（x）+ f '（x）\ delta + \ frac {1} {2} \ delta f' '（x）\ delta \ bigg）= f'（x ）+ f ''（x）\ delta = 0 \は\ delta =-\ frac {f '（x）} {f' '（x）} $を意味す$$

もし $$$f$ 二次関数これは絶対最小値になります。 最小値を繰り返し見つけたい場合は、最初の $$$x_0$ このルールに従って更新します。

$$

$$x_ {n + 1} = x_n- \ frac {f '（x_n）} {f' '（x_n）} = x_n-（f' '（x_n））^ {-1} f'（x_n）$$

時間が経つにつれて、ソリューションは最小限になります。



多次元の場合を考えます。 多次元関数があるとします $$$f：\ mathbb {R ^ n}$ その後：

$$

$$f '（x）\から\ nabla f（x）$$

$$

$$f ''（x）\ to H（f）（x）$$

どこで $$$H（f）（x）$ -ヘッセ行列（ヘッシアン）または2次導関数の行列。 これに基づいて、パラメーターを更新するには、次の式を使用します。

$$

$$x_ {n + 1} = x_n-（H（f）（x））^ {-1} \ nabla f（x_n）$$

ニュートン法の問題

ご覧のとおり、Newtonメソッドは2次のメソッドであり、通常の勾配降下よりもうまく機能します。これは、各ステップでローカルミニマムに移動する代わりに、関数が $$$f$ 二次およびテイラー級数の二次の展開はその良い近似です。



しかし、この方法には1つの大きなマイナスがあります。 コスト関数を最適化するには、ヘッセ行列またはヘッセ行列を見つける必要があります $$$H$ 。 置く $$$\ mathbb {x}$ パラメータのベクトルである場合：

$$

$$H（f）（\ mathbf {x}）= \ begin {pmatrix} \ frac {\ delta f} {\ delta x_1 \ delta x_1}＆\ frac {\ delta f} {\ delta x_1 \ delta x_2}＆ \ cdots＆\ frac {\ delta f} {\ delta x_1 \ delta x_n} \\ \ frac {\ delta f} {\ delta x_2 \ delta x_1}＆\ frac {\ delta f} {\ delta x_2 \ delta x_2 }＆\ cdots＆\ frac {\ delta f} {\ delta x_2 \ delta x_n} \\ \ vdots＆\ vdots＆\ ddots＆\ vdots \\ \ frac {\ delta f} {\ delta x_m \ delta x_1} ＆\ frac {\ delta f} {\ delta x_m \ delta x_2}＆\ cdots＆\ frac {\ delta f} {\ delta x_m \ delta x_n} \ end {pmatrix}$$

ご覧のとおり、ヘッセ行列はサイズの2次導関数の行列です $$$n \回n$ 計算には何が必要ですか $$$O（n ^ 2）$ 数百または数千のパラメータを持つネットワークにとって非常に重要な計算操作。 さらに、ニュートン法を使用して最適化問題を解決するには、逆ヘッセ行列を見つける必要があります $$$H ^ {-1}（f）（x）$ 、これのために、それはすべてのために明確に定義されるべきです $$$n$ 。

---

ヘシアンフリー最適化

HF最適化の主な考え方は、Newtonの方法を基礎とすることですが、より適切な方法を使用して2次関数を最小化することです。 ただし、最初に、将来必要になる基本的な概念を紹介します。

させる $$$\ theta =（\ mathbf W、\ mathbf b）$ -ネットワークパラメータ、ここで $$$\ mathbf W$ -重みの行列（重み）、 $$$\ mathbf b$ バイアスベクトル、次にネットワーク出力を呼び出します。 $$$f（x、\シータ）$ どこで $$$x$ -入力ベクトル。 $$$L（t、f（x、\ theta））$ -損失関数 $$$t$ -ターゲット値。 そして、すべてのトレーニング例（トレーニングバッチ）の損失の平均として最小化する関数を定義します。 $$$S$ ：

$$

$$h（\ theta）= \ frac {1} {| S |} \ sum _ {（x、y）\ in S} L（t、f（x、\ theta））$$

次に、ニュートンの方法に従って、2次のテイラー級数に展開して得られる2次関数を定義します。

$$

$$h（\ theta + \ delta）\ equiv M（\ delta）= h（\ theta）+ \ nabla h（\ theta）^ T \ delta + \ frac {1} {2} \ delta ^ TH \ delta \ qquad \ qquad（1）$$

さらに、 $$$\デルタ$ 上記の式からゼロに等しくすると、次のようになります。

$$

$$\ nabla M（\ delta）= \ nabla h（\ theta）+ H \ delta = 0 \ qquad \ qquad（2）$$

見つけるために $$$\デルタ$ 共役勾配法を使用します。

共役勾配法

共役勾配法（CG）は、次のタイプの線形方程式系を解くための反復法です。 $$$\ mathbf A \ mathbf x = \ mathbf b$ 。



簡単なCGアルゴリズム：

入力データ： $$$\ mathbf b$ 、 $$$\ mathbf A$ 、 $$$\ mathbf x_0$ 、 $$$i = 0$ -CGアルゴリズムのステップ

初期化：

1. $$$\ mathbf r_0 = \ mathbf b-\ mathbf A \ mathbf x_0$ -エラーベクトル（残差）
2. $$$\ mathbf d_0 = \ mathbf r_0$ -検索方向のベクトル

停止条件が満たされるまで繰り返します。

1. $$$\ alpha_i = \ frac {\ mathbf r_i ^ T \ mathbf r_i} {\ mathbf d_i ^ T \ mathbf A \ mathbf d}$
2. $$$\ mathbf x_ {i + 1} = \ mathbf x_i + \ alpha_i \ mathbf d_i$
3. $$$\ mathbf r_ {i + 1} = \ mathbf r_i-\ alpha_i \ mathbf A \ mathbf d_i$
4. $$$\ beta_i = \ frac {\ mathbf r_ {i + 1} ^ T \ mathbf r_ {i + 1}} {\ mathbf r_i ^ T \ mathbf r_i}$
5. $$$\ mathbf d_ {i + 1} = \ mathbf r_ {i + 1} + \ beta_i \ mathbf d_i$
6. $$$i = i + 1$

ここで、共役勾配法を使用して、方程式（2）を解くと、 $$$\デルタ$ これにより最小化されます（1）。 私たちの場合： $$$\ mathbf A \ equiv H、\ mathbf b \ equiv-\ nabla h（\ theta）、\ mathbf x \ equiv \ delta$ 。

CGアルゴリズムを停止します。 さまざまな基準に基づいて共役勾配法を停止できます。 二次関数の最適化の相対的な進捗に基づいてこれを行います $$$M$ ：

$$

$$s_i = \ frac {M（\ delta_i）-M（\ delta_ {i-w}）} {M（\ delta_i）-M（0）} \ qquad \ qquad（3）$$

どこで $$$w$ -進捗の価値を考慮する「ウィンドウ」のサイズ、 $$$w =最大（10、i / 10）$ 。 停止条件は次のとおりです。 $$$s_i <0.0001$ 。

これで、HF最適化の主な特徴は 、ヘッシアンを直接見つける必要はなく、ベクトルでその積の結果を見つけるだけであることがわかります。

ベクトルによるヘシアン乗算

前述したように、この方法の魅力は、ヘッシアンを直接数える必要がないことです。 ベクトルによる2次導関数の行列の積の結果を計算する必要があるだけです。 このためにあなたは想像することができます $$$H（\シータ）v$ の派生物として $$$H（\シータ）$ 方向に $$$v$ ：

$$

$$H（\ theta）v = \ lim _ {\ epsilon \ to0} \ frac {\ nabla h（\ theta + \ epsilon v）-\ nabla h（\ theta）} {\ epsilon}$$

しかし、実際にこの式を使用すると、十分に小さい計算に関連する多くの問題が発生する可能性があります $$$\イプシロン$ 。 そのため、ベクトルによる行列の正確な積を計算する方法があります。 微分演算子を紹介します $$$R_vx$ 。 ある程度の導関数を示します $$$x$ 依存する $$$\シータ$ 方向に $$$v$ ：

$$

$$R_vx = \ lim _ {\ epsilon \ to0} \ frac {x（\ theta + \ epsilon v）-x（\ theta）} {\ epsilon} = \ frac {\ delta x} {\ delta \ theta} v$$

これは、ヘッセ行列の積をベクトルで計算するには、次の計算が必要であることを示しています。

$$

$$Hv = R（\ nabla h（\ theta））\ qquad \ qquad（4）$$

HF最適化のいくつかの改善

1.一般化ニュートンガウス行列（一般化ガウスニュートン行列）。

ヘッセ行列の不定性は、非凸（非凸）関数を最適化するための問題であり、2次関数の下限の欠如につながる可能性があります。 $$$M$ そしてその結果、その最小値を見つけることは不可能です。 この問題は多くの方法で解決できます。 たとえば、信頼区間を導入すると、曲率行列に正の半確定成分を追加する罰金に基づいて最適化または減衰が制限されます $$$H$ そして彼女を前向きにした。



実際の結果に基づいて、この問題を解決する最良の方法は、ニュートンガウス行列を使用することです $$$G$ ヘッセ行列の代わりに：

$$

$$G = \ frac {1} {| S |} \ sum _ {（x、y）\ in S} J ^ TH_LJ \ qquad \ qquad（5）$$

どこで $$$J$ -ヤコビアン、 $$$H_l$ -損失関数の二次導関数の行列 $$$L（t、f（x、\ theta））$ 。

行列の積を見つけるには $$$G$ ベクトルで $$$v$ ： $$$Gv = j ^ th_ljv$ 、最初にベクトルによるヤコビアンの積を求めます。

$$

$$Jv = R_v（f（x、\ theta））$$

次に、ベクトルの積を計算します $$$Jv$ 行列へ $$$H_l$ そして最後に行列を掛けます $$$J$ に $$$H_LJv$ 。



2.ダンピング。

標準のニュートン法では、強く非線形な目的関数の最適化が不十分な場合があります。 この理由は、最適化の初期段階では、開始点が最小点から遠いため、非常に大きく積極的である可能性があるためです。 この問題を解決するために、ダンプが使用されます-二次関数を変更する方法 $$$M$ または、新しい制限が $$$\デルタ$ そのような制限内にあります $$$M$ 良い近似のままになります $$$h$ 。

Tikhonovの正則化（Tikhonov正則化）またはTikhonovのダンピング（Tikhonov減衰）。 （機械学習のコンテキストで一般的に使用される「正規化」という用語と混同しないでください）これは、関数に二乗ペナルティを追加する最も有名なダンプ方法です $$$M$ ：

$$

$$\ hat {M}（\ delta）\ equiv M（\ delta）+ \ frac {\ lambda} {2} \ delta ^ T \ delta = f（\ theta）+ \ nabla h（\ theta）^ T \ delta + \ frac {1} {2} \ delta ^ T \ hat {H} \ delta$$

どこで $$$\ hat {H} = H + \ lambda I$ 、 $$$\ lambda \ geq0$ -ダンプパラメーター。 計算 $$$Hv$ このように行われます：

$$

$$\ hat {H} v =（H + \ lambda I）v = Hv + \ lambda v \ qquad \ qquad（6）$$

3. Levenberg-Marquardtのヒューリスティック（Levenberg-Marquardtヒューリスティック）。

チホノフのダンピングは、パラメーターの動的調整によって特徴付けられます $$$\ラムダ$ 。 変更 $$$\ラムダ$ LM-メソッドのコンテキストでよく使用されるLevenberg-Marquardtルールに従います（最適化メソッドは、Newtonメソッドの代替です）。 LM-ヒューリスティックを使用するには、いわゆる縮小率を計算する必要があります。

$$

$$\ rho = \ frac {h（\ theta_k + \ delta_k）-h（\ delta_k）} {M_k（\ delta_k）-M_k（0）} = \ frac {h（\ theta_k + \ delta_k）-h（\ delta_k） } {\ nabla h（\ theta_k）^ T \ delta_k + \ frac {1} {2} \ delta_k ^ TH \ delta_k} \ qquad \ qquad（7）$$

どこで $$$k$ -HFアルゴリズムのステップ番号、 $$$\ delta_k$ -CG最小化の作業の結果。

Levenberg-Marquardtのヒューリスティックによれば、更新規則が得られます $$$\ラムダ$ ：

$$

$$\ begin {cases} if \ \ rho> 3/4 \ then \ \ lambda \ gets（2/3）\ lambda \\ if \ \ rho <1/4 \ then \ \ lambda \ gets（3/2） \ lambda \ end {cases} \ qquad \ qquad（8）$$

4.共役勾配のアルゴリズムの初期条件（事前調整）。

HF最適化のコンテキストでは、いくつかの可逆変換行列があります $$$C$ 一緒に変わる $$$M$ そのような $$$\ delta = C ^ {-1} \ガンマ$ 代わりに $$$\デルタ$ 最小化する $$$\ガンマ$ 。 この機能をCGアルゴリズムに適用するには、変換されたエラーベクトルの計算が必要です。 $$$y_i = P ^ {-1} r_i$ どこで $$$P = C ^ TC$ 。



簡単なPCG（前処理付き共役勾配）アルゴリズム：

入力データ： $$$\ mathbf b$ 、 $$$\ mathbf A$ 、 $$$\ mathbf x_0$ 、 $$$P$ 、 $$$i = 0$ -CGアルゴリズムのステップ

初期化：

1. $$$\ mathbf r_0 = \ mathbf b-\ mathbf A \ mathbf x_0$ -エラーベクトル（残差）
2. $$$\ mathbf y_0$ -方程式の解 $$$Py_0 = r_0$
3. $$$\ mathbf d_0 = \ mathbf y_0$ -検索方向のベクトル

停止条件が満たされるまで繰り返します。

1. $$$\ alpha_i = \ frac {\ mathbf r_i ^ T \ mathbf y_i} {\ mathbf d_i ^ T \ mathbf A \ mathbf d}$
2. $$$\ mathbf x_ {i + 1} = \ mathbf x_i + \ alpha_i \ mathbf d_i$
3. $$$\ mathbf r_ {i + 1} = \ mathbf r_i-\ alpha_i \ mathbf A \ mathbf d_i$
4. $$$\ mathbf y_ {i + 1}$ -方程式の解 $$$Py_ {i + 1} = r_i$
5. $$$\ beta_i = \ frac {\ mathbf r_ {i + 1} ^ T \ mathbf y_ {i + 1}} {\ mathbf r_i ^ T \ mathbf y_i}$
6. $$$\ mathbf d_ {i + 1} = \ mathbf y_ {i + 1} + \ beta_i \ mathbf d_i$
7. $$$i = i + 1$

マトリックス選択 $$$P$ 非常に簡単な作業です。 また、実際には、（フルランクの行列の代わりに）対角行列を使用すると、かなり良い結果が得られます。 マトリックスを選択するためのオプションの1つ $$$P$ -これは対角フィッシャー行列（経験的フィッシャー対角）の使用です：

$$

$$P = diag（\ bar {F}）= \ frac {1} {| S |} \ sum _ {（x、y）\ in S}（\ nabla（L（t、f（x、\ theta）） ）^ 2 \ qquad \ qquad（9）$$

5. CGの初期化-アルゴリズム。

イニシャルを初期化することをお勧めします $$$\ delta_0$ 、共役勾配アルゴリズムの場合、値 $$$\ delta_k$ HFアルゴリズムの前のステップで見つかりました。 この場合、いくつかの減衰定数を使用できます。 $$$\ delta_0 = \ epsilon \ delta_k、\ \ epsilon \ in（0、1）$ 。 インデックスは注目に値します $$$k$ HFアルゴリズムのステップ番号を指し、順番にインデックス0 $$$\ delta_0$ CGアルゴリズムの初期ステップを指します。



完全なヘシアンフリー最適化アルゴリズム：

入力データ： $$$\シータ$ 、 $$$\ラムダ$ -ダンプパラメーター $$$k$ -アルゴリズムの反復のステップ

初期化：

1. $$$\ delta_0 = 0$

メインのHF最適化サイクル：

1. 行列を計算する $$$P$
2. 見つける $$$\ delta_k$ CGまたはPCGを使用して最適化問題を解決します。 $$$\ delta_k = CG（-\ nabla h（\ theta_k）、H、\ epsilon \ delta_ {k-1}、P）$
3. ダンプパラメーターの更新 $$$\ラムダ$ Levenberg-Marquardtヒューリスティックを使用
4. $$$\ theta_ {k + 1} = \ theta_k + \ alpha \ theta_k$ 、 $$$\ alpha$ -学習率パラメーター
5. $$$k = k + 1$

したがって、ヘッセ行列を使用しない最適化手法により、大次元関数の最小値を見つける問題を解決できます。 ヘッセ行列を直接見つける必要はありません。

---

TensorFlowでのHF最適化の実装

理論は確かに優れていますが、実際にこの最適化手法を実装して、その結果を確認してみましょう。 HFアルゴリズムを記述するために、PythonとTensorFlow深層学習ライブラリを使用しました。 その後、パフォーマンスチェックとして、最適化のためにHFメソッドを使用して、XORおよびMNISTデータセット上のいくつかのレイヤーで直接配信ネットワークをトレーニングしました。



共役勾配法の実装（TensorFlow計算グラフの作成）。

def __conjugate_gradient(self, gradients): """ Performs conjugate gradient method to minimze quadratic equation and find best delta of network parameters. gradients: list of Tensorflow tensor objects Network gradients. return: Tensorflow tensor object Update operation for delta. return: Tensorflow tensor object Residual norm, used to prevent numerical errors. return: Tensorflow tensor object Delta loss. """ with tf.name_scope('conjugate_gradient'): cg_update_ops = [] prec = None #  P   (9) if self.use_prec: if self.prec_loss is None: graph = tf.get_default_graph() lop = self.loss.op.node_def self.prec_loss = graph.get_tensor_by_name(lop.input[0] + ':0') batch_size = None if self.batch_size is None: self.prec_loss = tf.unstack(self.prec_loss) batch_size = self.prec_loss.get_shape()[0] else: self.prec_loss = [tf.gather(self.prec_loss, i) for i in range(self.batch_size)] batch_size = len(self.prec_loss) prec = [[g**2 for g in tf.gradients(tf.gather(self.prec_loss, i), self.W)] for i in range(batch_size)] prec = [(sum(tensor) + self.damping)**(-0.75) for tensor in np.transpose(np.array(prec))] #    Ax = None if self.use_gnm: Ax = self.__Gv(self.cg_delta) else: Ax = self.__Hv(gradients, self.cg_delta) b = [-grad for grad in gradients] bAx = [b - Ax for b, Ax in zip(b, Ax)] condition = tf.equal(self.cg_step, 0) r = [tf.cond(condition, lambda: tf.assign(r, bax), lambda: r) for r, bax in zip(self.residuals, bAx)] d = None if self.use_prec: d = [tf.cond(condition, lambda: tf.assign(d, p * r), lambda: d) for p, d, r in zip(prec, self.directions, r)] else: d = [tf.cond(condition, lambda: tf.assign(d, r), lambda: d) for d, r in zip(self.directions, r)] Ad = None if self.use_gnm: Ad = self.__Gv(d) else: Ad = self.__Hv(gradients, d) residual_norm = tf.reduce_sum([tf.reduce_sum(r**2) for r in r]) alpha = tf.reduce_sum([tf.reduce_sum(d * ad) for d, ad in zip(d, Ad)]) alpha = residual_norm / alpha if self.use_prec: beta = tf.reduce_sum([tf.reduce_sum(p * (r - alpha * ad)**2) for r, ad, p in zip(r, Ad, prec)]) else: beta = tf.reduce_sum([tf.reduce_sum((r - alpha * ad)**2) for r, ad in zip(r, Ad)]) self.beta = beta beta = beta / residual_norm for i, delta in reversed(list(enumerate(self.cg_delta))): update_delta = tf.assign(delta, delta + alpha * d[i], name='update_delta') update_residual = tf.assign(self.residuals[i], r[i] - alpha * Ad[i], name='update_residual') p = 1.0 if self.use_prec: p = prec[i] update_direction = tf.assign(self.directions[i], p * (r[i] - alpha * Ad[i]) + beta * d[i], name='update_direction') cg_update_ops.append(update_delta) cg_update_ops.append(update_residual) cg_update_ops.append(update_direction) with tf.control_dependencies(cg_update_ops): cg_update_ops.append(tf.assign_add(self.cg_step, 1)) cg_op = tf.group(*cg_update_ops) dl = tf.reduce_sum([tf.reduce_sum(0.5*(delta*ax) + grad*delta) for delta, grad, ax in zip(self.cg_delta, gradients, Ax)]) return cg_op, residual_norm, dl
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

行列を計算するコード $$$P$ 初期条件（前提条件）を見つけるには、次のようになります。 同時に、Tensorflowは提示されたトレーニング例全体の勾配を計算した結果を要約するため、各例で勾配を個別に取得するために少しひねる必要があり、これが解の数値安定性に影響を与えました。 したがって、彼らが言うように、あなた自身の危険とリスクで、事前調整の使用が可能です。

  prec = [[g**2 for g in tf.gradients(tf.gather(self.prec_loss, i), self.W)] for i in range(batch_size)]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ベクトル（4）によるヘッセ行列の積の計算。 この場合、Tikhonovダンプが使用されます（6）。

  def __Hv(self, grads, vec): """ Computes Hessian vector product. grads: list of Tensorflow tensor objects Network gradients. vec: list of Tensorflow tensor objects Vector that is multiplied by the Hessian. return: list of Tensorflow tensor objects Result of multiplying Hessian by vec. """ grad_v = [tf.reduce_sum(g * v) for g, v in zip(grads, vec)] Hv = tf.gradients(grad_v, self.W, stop_gradients=vec) Hv = [hv + self.damp_pl * v for hv, v in zip(Hv, vec)] return Hv
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

一般化されたニュートン・ガウス行列（5）を使用したいとき、小さな問題に遭遇しました。 つまり、TensorFlowは、他のTheanoディープラーニングフレームワーク（Theanoにはこのために特別に設計されたRop関数があります）のように、ベクトルに対するヤコビアンの仕事を計算する方法を知りません。 TensorFlowでアナログ操作を行う必要がありました。

  def __Rop(self, f, x, vec): """ Computes Jacobian vector product. f: Tensorflow tensor object Objective function. x: list of Tensorflow tensor objects Parameters with respect to which computes Jacobian matrix. vec: list of Tensorflow tensor objects Vector that is multiplied by the Jacobian. return: list of Tensorflow tensor objects Result of multiplying Jacobian (df/dx) by vec. """ r = None if self.batch_size is None: try: r = [tf.reduce_sum([tf.reduce_sum(v * tf.gradients(f, x)[i]) for i, v in enumerate(vec)]) for f in tf.unstack(f)] except ValueError: assert False, clr.FAIL + clr.BOLD + 'Batch size is None, but used '\ 'dynamic shape for network input, set proper batch_size in '\ 'HFOptimizer initialization' + clr.ENDC else: r = [tf.reduce_sum([tf.reduce_sum(v * tf.gradients(tf.gather(f, i), x)[j]) for j, v in enumerate(vec)]) for i in range(self.batch_size)] assert r is not None, clr.FAIL + clr.BOLD +\ 'Something went wrong in Rop computation' + clr.ENDC return r
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、一般化されたニュートン・ガウス行列の積をベクトルで既に実現しています。

  def __Gv(self, vec): """ Computes the product G by vec = JHJv (G is the Gauss-Newton matrix). vec: list of Tensorflow tensor objects Vector that is multiplied by the Gauss-Newton matrix. return: list of Tensorflow tensor objects Result of multiplying Gauss-Newton matrix by vec. """ Jv = self.__Rop(self.output, self.W, vec) Jv = tf.reshape(tf.stack(Jv), [-1, 1]) HJv = tf.gradients(tf.matmul(tf.transpose(tf.gradients(self.loss, self.output)[0]), Jv), self.output, stop_gradients=Jv)[0] JHJv = tf.gradients(tf.matmul(tf.transpose(HJv), self.output), self.W, stop_gradients=HJv) JHJv = [gv + self.damp_pl * v for gv, v in zip(JHJv, vec)] return JHJv
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

主な学習プロセスの機能を以下に示します。 まず、CG / PCGを使用して2次関数が最小化され、次にネットワークの重みの主な更新が行われます。 Levenberg-Marquardtヒューリスティックに基づくダンプパラメーターも調整されます。

  def minimize(self, feed_dict, debug_print=False): """ Performs main training operations. feed_dict: dictionary Input training batch. debug_print: bool If True prints CG iteration number. """ self.sess.run(tf.assign(self.cg_step, 0)) feed_dict.update({self.damp_pl:self.damping}) if self.adjust_damping: loss_before_cg = self.sess.run(self.loss, feed_dict) dl_track = [self.sess.run(self.ops['dl'], feed_dict)] self.sess.run(self.ops['set_delta_0']) for i in range(self.cg_max_iters): if debug_print: d_info = clr.OKGREEN + '\r[CG iteration: {}]'.format(i) + clr.ENDC sys.stdout.write(d_info) sys.stdout.flush() k = max(self.gap, i // self.gap) rn = self.sess.run(self.ops['res_norm'], feed_dict) #      if rn < self.cg_num_err: break self.sess.run(self.ops['cg_update'], feed_dict) dl_track.append(self.sess.run(self.ops['dl'], feed_dict)) #  ,    (3) if i > k: stop = (dl_track[i+1] - dl_track[i+1-k]) / dl_track[i+1] if not np.isnan(stop) and stop < 1e-4: break if debug_print: sys.stdout.write('\n') sys.stdout.flush() if self.adjust_damping: feed_dict.update({self.damp_pl:0}) dl = self.sess.run(self.ops['dl'], feed_dict) feed_dict.update({self.damp_pl:self.damping}) self.sess.run(self.ops['train'], feed_dict) if self.adjust_damping: loss_after_cg = self.sess.run(self.loss, feed_dict) #  (7) reduction_ratio = (loss_after_cg - loss_before_cg) / dl # - (8) if reduction_ratio < 0.25 and self.damping > self.damp_num_err: self.damping *= 1.5 elif reduction_ratio > 0.75 and self.damping > self.damp_num_err: self.damping /= 1.5
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

HF最適化のテスト

記述されたHFオプティマイザーをテストします。このため、XORデータセットを使用した簡単な例を使用し、MNISTデータセットを使用したより複雑な例を使用します。 学習成果を確認し、いくつかの情報を視覚化するために、TesnorBoardを使用します。 また、TensorFlow計算のかなり複雑なグラフが取得されたことにも注意してください。





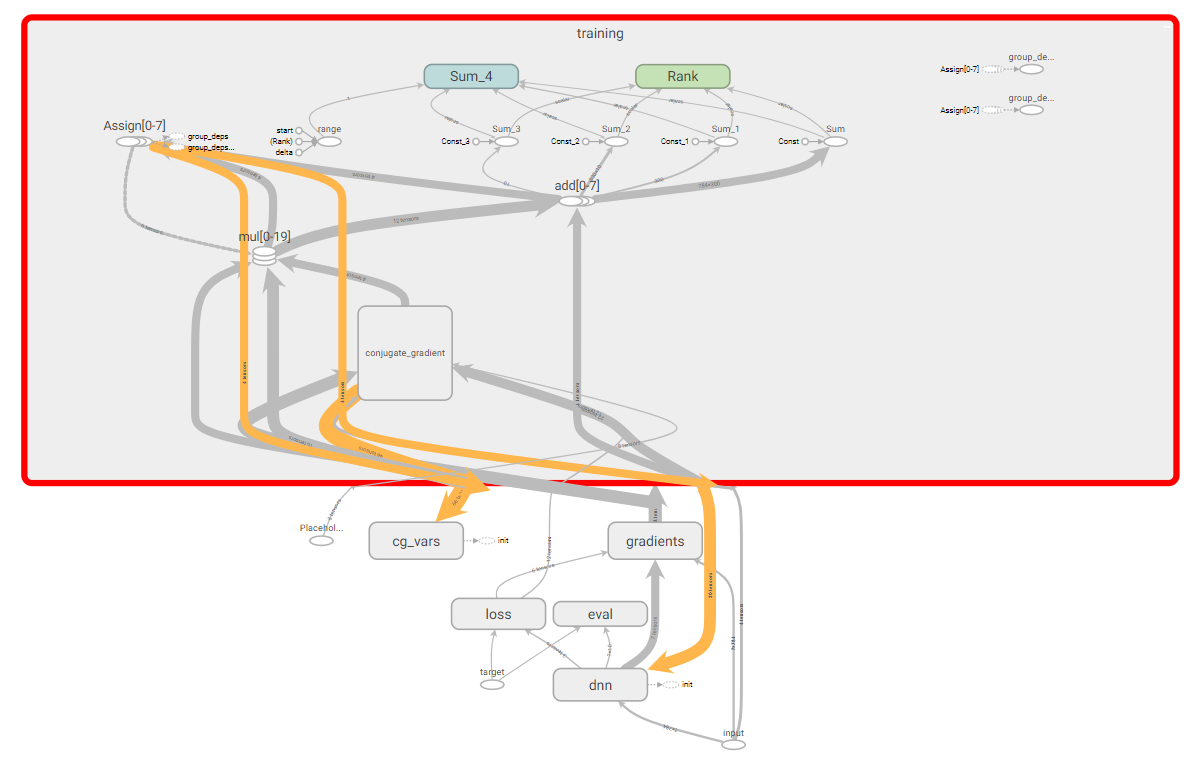
TensorFlow Computingグラフ。



XORデータセットに関するネットワークアーキテクチャとトレーニング。

2つの入力ニューロン、2つの隠れニューロン、1つの出力のサイズの単純なネットワークを作成しましょう。 アクティベーション関数として、シグモイドを使用します。 損失関数として、対数損失を使用します。

  #   """ Log-loss cost function """ loss = tf.reduce_mean(( (y * tf.log(out)) + ((1 - y) * tf.log(1.0 - out)) ) * -1, name='log_loss') #XOR  XOR_X = [[0,0],[0,1],[1,0],[1,1]] XOR_Y = [[0],[1],[1],[0]] #  sess = tf.Session() hf_optimizer = HFOptimizer(sess, loss, y_out, dtype=tf.float64, use_gauss_newton_matrix=True) init = tf.initialize_all_variables() sess.run(init) #  max_epoches = 100 print('Begin Training') for i in range(max_epoches): feed_dict = {x: XOR_X, y: XOR_Y} hf_optimizer.minimize(feed_dict=feed_dict) if i % 10 == 0: print('Epoch:', i, 'cost:', sess.run(loss, feed_dict=feed_dict)) print('Hypothesis ', sess.run(out, feed_dict=feed_dict))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、HF最適化（ヘッセ行列を使用）、HF最適化（ニュートンガウス行列を使用）、および0.01に等しい学習速度パラメーターを使用した通常の勾配降下を使用して、学習結果を比較します。 反復回数は100です。





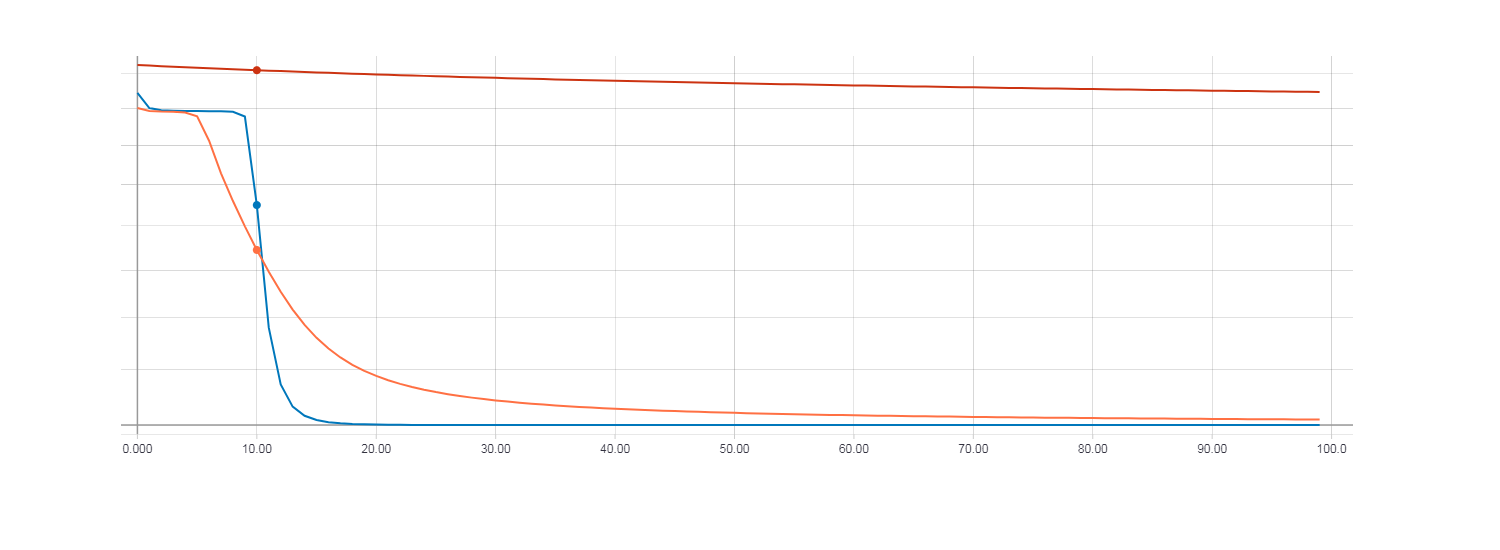
勾配降下の損失（赤線）。 ヘッセ行列を使用したHF最適化の損失（オレンジ色の線）。 ニュートンガウス行列によるHF最適化の損失（青線）。



同時に、Newton-Gauss行列を使用したHF最適化が最速で収束する一方で、100回の反復の勾配降下では非常に小さいことが判明しました。 勾配降下の損失関数がHF最適化に匹敵するためには、約100,000回の反復が必要でした。





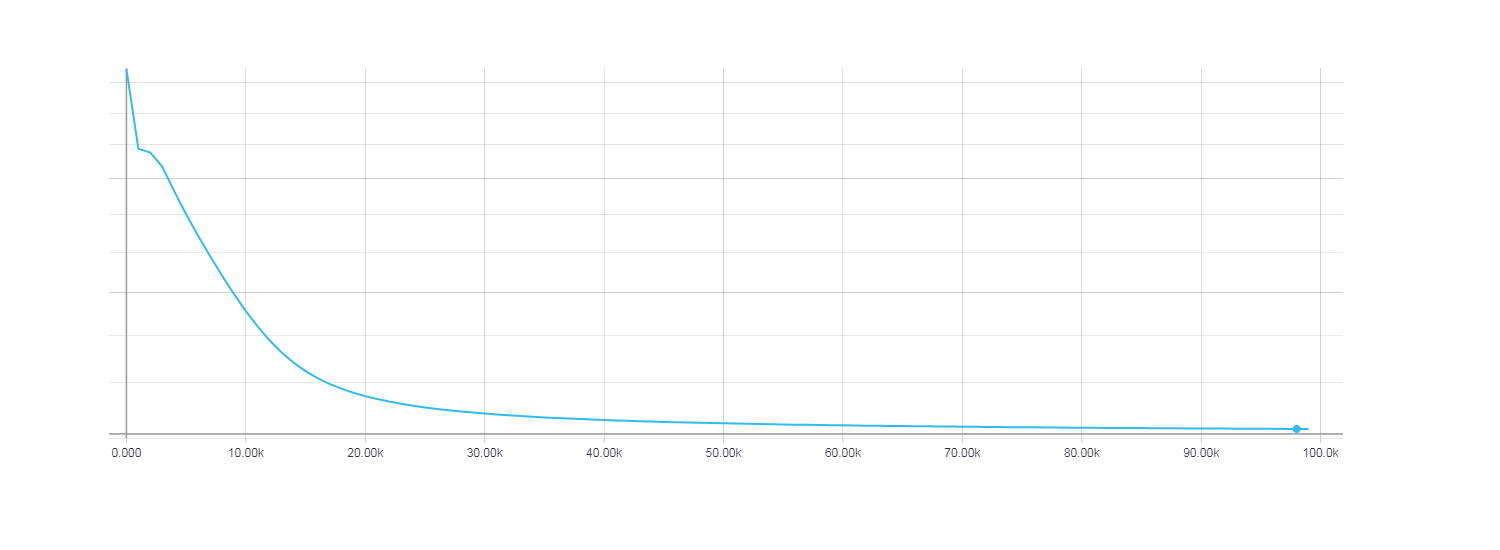
勾配降下の損失、100,000回の反復。



MNISTデータセットに関するネットワークアーキテクチャとトレーニング。

手書きの数字認識の問題を解決するために、入力ニューロン784、非表示300、出力10のサイズのネットワークを作成します。 損失の関数として、クロスエントロピーを使用します。 トレーニング中に提供されるミニバッチのサイズは50です。

  with tf.name_scope('loss'): one_hot = tf.one_hot(t, n_outputs, dtype=tf.float64) xentropy = tf.nn.softmax_cross_entropy_with_logits(labels=one_hot, logits=y_out) loss = tf.reduce_mean(xentropy, name="loss") with tf.name_scope("eval"): correct = tf.nn.in_top_k(tf.cast(y_out, tf.float32), t, 1) accuracy = tf.reduce_mean(tf.cast(correct, tf.float64)) n_epochs = 10 batch_size = 50 with tf.Session() as sess: """ Initializing hessian free optimizer """ hf_optimizer = HFOptimizer(sess, loss, y_out, dtype=tf.float64, batch_size=batch_size, use_gauss_newton_matrix=True) init = tf.global_variables_initializer() init.run() #   for epoch in range(n_epochs): n_batches = mnist.train.num_examples // batch_size for iteration in range(n_batches): x_batch, t_batch = mnist.train.next_batch(batch_size) hf_optimizer.minimize({x: x_batch, t: t_batch}) if iteration%10==0: print('Batch:', iteration, '/', n_batches) acc_train = accuracy.eval(feed_dict={x: x_batch, t: t_batch}) acc_test = accuracy.eval(feed_dict={x: mnist.test.images, t: mnist.test.labels}) print('Loss:', sess.run(loss, {x: x_batch, t: t_batch})) print('Target', t_batch[0]) print('Out:', sess.run(y_out_sm, {x: x_batch, t: t_batch})[0]) print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test) acc_train = accuracy.eval(feed_dict={x: x_batch, t: t_batch}) acc_test = accuracy.eval(feed_dict={x: mnist.test.images, t: mnist.test.labels}) print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

XORの場合と同様に、HF最適化（ヘッセ行列）、HF最適化（ニュートンガウス行列）、および学習速度パラメーター0.01の通常の勾配降下を使用して、学習結果を比較します。 反復回数は200、つまりです。 ミニバッチのサイズが50の場合、200は完全な時代ではありません（トレーニングセットのすべての例が使用されるわけではありません）。 すべてをより速くテストするためにこれを行いましたが、これでも一般的な傾向が見えます。





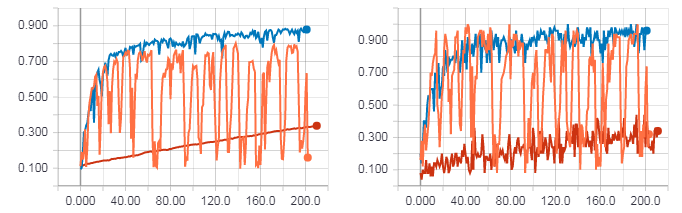
左の図は、テストサンプルの精度です。 右の図は、トレーニングサンプルの精度です。 勾配降下の精度（赤線）。 ヘッセ行列（オレンジ色の線）を使用したHF最適化の精度。 ニュートンガウス行列を使用したHF最適化の精度（青線）。





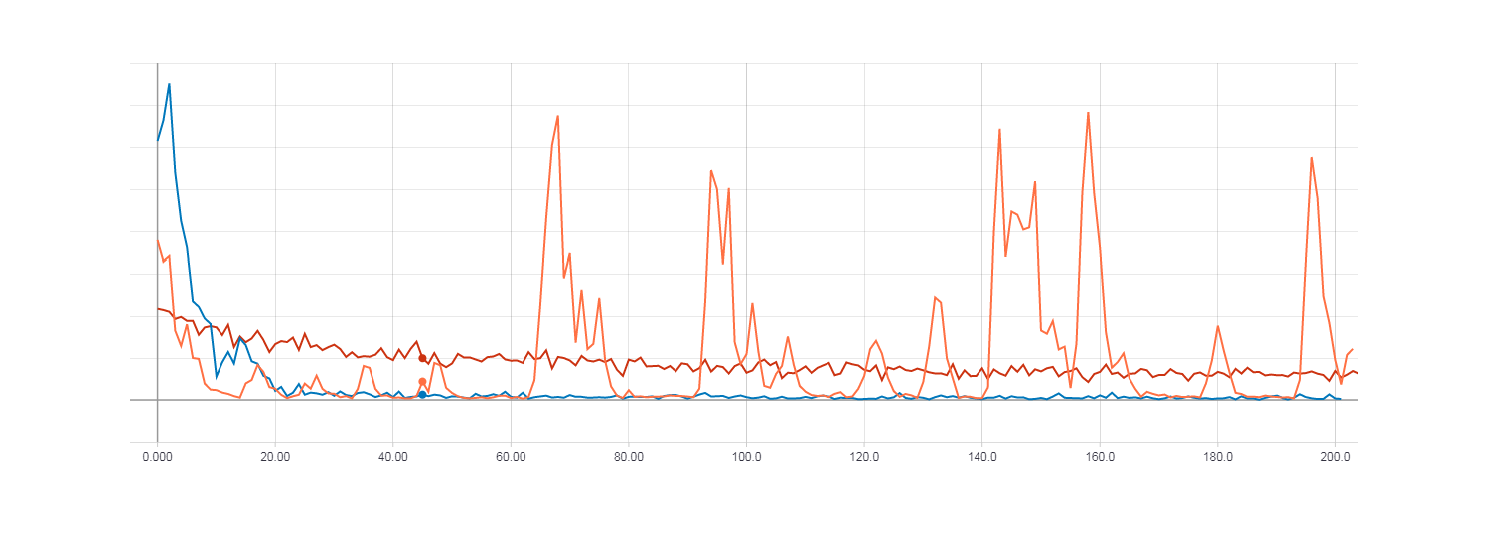
勾配降下の損失（赤線）。 ヘッセ行列を使用したHF最適化の損失（オレンジ色の線）。 ニュートンガウス行列によるHF最適化の損失（青線）。



上の図からわかるように、ヘッセ行列を使用したHF最適化はあまり安定して動作しませんが、いくつかの時代で学習すると最終的に収束します。 最良の結果は、ニュートンガウスマトリックスを使用したHF最適化によって示されます。





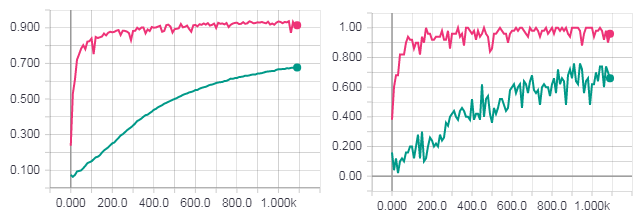
学習の完全な時代。 左の図は、テストサンプルの精度です。 右の図は、トレーニングサンプルの精度です。 勾配降下の精度（青緑色の線）。 ニュートンガウス行列を使用したHF最適化の損失（ピンクの線）。





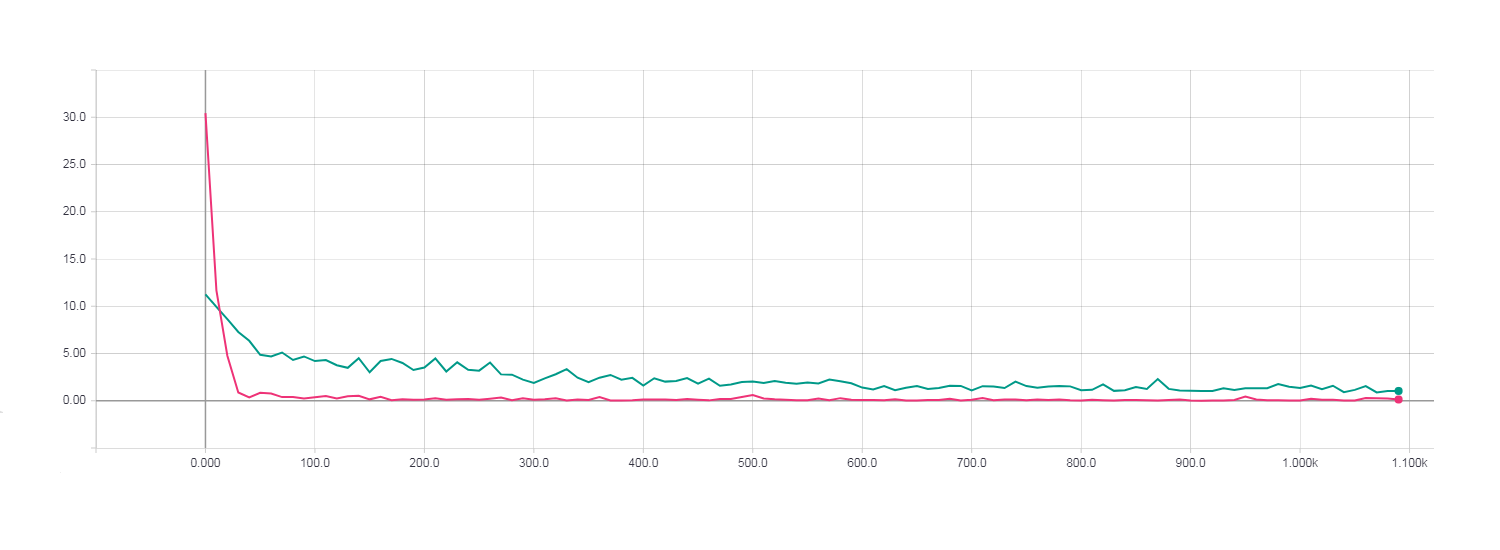
学習の完全な時代。 勾配降下の損失（青緑色の線）。 ニュートンガウス行列を使用したHF最適化の損失（ピンクの線）。



共役勾配のアルゴリズムの初期条件で共役勾配の方法を使用すると（事前調整）、計算自体が大幅に遅くなり、通常のCGよりも速く収束しませんでした。





PCGアルゴリズムを使用したHF最適化の損失。



これらのすべてのグラフから、Newton-Gauss行列と標準共役勾配法を使用したHF最適化によって最良の結果が示されたことがわかります。

完全なコードはGitHubで表示できます。

---

まとめ

その結果、PythonでのHFアルゴリズムの実装は、TensorFlowライブラリを使用して作成されました。 作成中に、アルゴリズムの主な機能を実装するときに、いくつかの問題が発生しました。つまり、Newton-Gauss行列のサポートと事前調整です。 これは、TensorFlowが私たちが望むほど柔軟なライブラリではなく、研究用に設計されていないためです。 実験目的では、Theanoを使用するほうが自由度が高くなるため、やはり良いです。 しかし、私は最初にこれをすべてTensorFlowで行うことにしました。 プログラムがテストされ、ニュートンガウス行列を使用したHFアルゴリズムが最良の結果を与えることがわかりました。 共役勾配のアルゴリズムの初期条件（事前調整）を使用すると、不安定な数値結果が得られ、計算が大幅に遅くなりましたが、これはTensorFlowの特性によるものと思われます（事前調整の実装のために、私は非常にゆがめなければなりませんでした）。

---

ソース

この記事では、アルゴリズムの主要な本質を理解できるように、ヘッセ行列の理論的側面-無料の最適化について簡単に説明します。 素材の詳細な説明が必要な場合は、基本的な理論情報を取得した情報源を引用します。この情報に基づいて、PythonがHFメソッドを実装しました。



1） ヘシアンを使用しない最適化によるディープでリカレントなネットワークのトレーニング（James MartensおよびIlya Sutskever、トロント大学）-HFの完全な説明-最適化。

2） ヘッセ行列のない最適化によるディープラーニング（James Martens、トロント大学）-HFを使用した結果を含む記事-最適化。

3） ヘッセ行列による高速完全乗算（Barak A. Pearlmutter、Siemens Corporate Research） -ヘッセ行列とベクトルの乗算の詳細な説明。

4） 苦痛を伴わない共役勾配法の紹介（Jonathan Richard Shewchuk、カーネギーメロン大学） -共役勾配法の詳細な説明。