R-回帰を意味します

統計は最近、新しくて騒がしい分野である機械学習とビッグデータから強力なPRサポートを受けました。 この波に乗ろうとする人々は、回帰方程式と仲良くする必要があります。 2-3のコツを学んで試験に合格するだけでなく、日常生活の問題を解決できるようにすることをお勧めします。変数間の関係を見つけ、理想的には信号とノイズを区別できるようにします。

この目的のために、このようなタスクに最適なプログラミング言語と開発環境Rを使用します。 同時に、Habrapostの評価が自分の記事の統計に依存していることを確認します。

回帰分析の概要

相関がある場合 $$$F（y）= F（x、y）$ 変数y



とx



間で、2つの量の間の関数関係を決定することが必要になります。 平均値 $$$\ mu_ {1y} = f（x）$ x



y



回帰と呼ばれます。

回帰分析の基礎は最小二乗法（LSM）であり 、これに従って関数は回帰方程式として採用されます $$$y = f（x）$ 平方差の合計が $$$s = \ sum_ {i = 1} ^ n [y_i-f（x）_i] ^ 2$ 最小限です。

カールガウスは18歳でOLSを発見、またはむしろ再現しましたが、結果は1805年にルジャンドルによって最初に公開されました。未検証のデータによると、この方法は古代中国で知られていた。 ヨーロッパ人はこの秘密を明かさず、1801年の小惑星セレスの軌跡を助けて発見し、生産に成功しました。

機能の種類 $$$y = f（x）$ 、原則として、事前に決定され、最小二乗法を使用して、未知のパラメータの最適値が選択されます。 散布メトリック $$$y_i$ 回帰の周り $$$f（x）$ 分散です。

$$

$$D = \ frac {1} {n-k} \ sum_ {i = 1} ^ n [y_i-f（x）_i] ^ 2$$

• k
  
  
  
  は、回帰方程式系の係数の数です。

最も一般的に使用される線形回帰モデル、およびすべての非線形依存関係 $$$y = f（x）$ 代数的トリック、変数y



およびx



さまざまな変換の助けを借りて線形形式に導きます。

線形回帰

線形回帰方程式は次のように書くことができます

$$

$$y = x_1 + \ beta_1 + ... x_k \ beta_k + \イプシロン$$

マトリックス形式では、

$$

$$y = X \ベータ+ \イプシロン$$

• yは従属変数です。
• xは独立変数です。
• β-OLSを使用して見つける必要がある係数。
• εは、エラー、原因不明のエラー、および線形関係からの逸脱です。

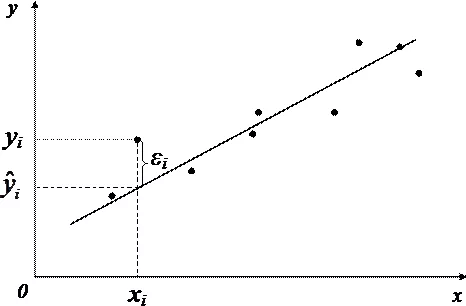
ランダム変数 $$$y_i$ 2つの用語の合計として解釈できます。

• $$$y_i$ - 全分散 （TSS）。
• $$$\ widehat {y_i}$ - 分散の一部 （ESS）を説明しました 。
• $$$\ epsilon_i = y_i-\ widehat {y_i}$ - 分散の残余部分 （RSS）。

もう1つの重要な概念は、相関係数R ²です。

$$

$$R ^ 2 = 1-ESS / TSS$$

線形回帰の制限

線形回帰モデルを使用するには、変数の分布とプロパティに関していくつかの仮定が必要です。

1. 実際、 直線性 。 係数kによる独立変数のベクトルの増加または減少は、同様に係数kによる従属変数の変化につながります。
2. 係数行列にはフルランクがあります 。つまり、独立変数のベクトルは線形独立です。
3. 外因性独立変数 - $$$E [\ epsilon_i | x_ {j1}、x_ {j2}、... x_ {jk}] = 0$ 。 この要件は、独立変数の助けを借りてエラーの数学的期待を説明できないことを意味します。
4. 分散の均一性と自己相関の欠如 。 各εiは同じ最終分散σ2を持ち、別のεiと相関しません。 これにより、線形回帰モデルの適用性が大幅に制限されます。条件が満たされていることを確認する必要があります。そうしないと、検出された変数の関係が誤って解釈されます。

上記の条件が満たされていないことを確認する方法は？ まあ、まず、かなり頻繁にこれはチャートの肉眼で見ることができます。

分散の不均一性

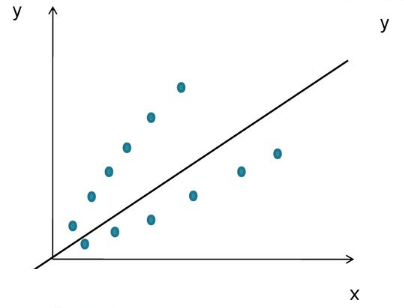
独立変数の増加に伴って分散が増加すると、漏斗型のグラフが作成されます。

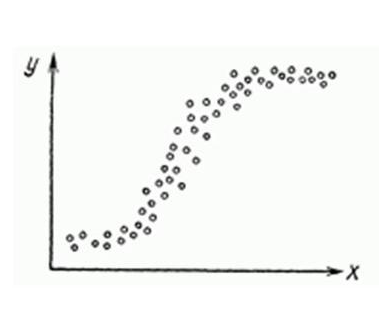
場合によっては、非線形回帰もファッショナブルであり、グラフで非常に明確に見ることができます。

それにもかかわらず、線形回帰の条件が満たされているか違反されているかを判断するための非常に厳密な正式な方法があります。

• 自己相関は、 Darbin-Watson統計 （ 0≤d≤4）によって検証されます。 自己相関がない場合、基準の値はd≈2で、正の自己相関d≈0、負の-d≈4です。
• 分散不均一性- ホワイトテスト 、 $$$\ chi {^ 2} _ {obs} = nR ^ 2$ で $$$\ chi {^ 2} _ {obs}> \ chi {^ 2} _ {\ alpha; m-1}$ 帰無仮説は棄却され、不均一分散の存在が確認されます。 同じものを使用する $$$\ chi {^ 2} _ {obs}$ Broysch-Paganテストを引き続き適用できます。
• 多重共線性-独立変数間の相互線形関係がないという条件の違反。 検証にはVIF（Variance Inflation Factor）がよく使用されます。

$$

$$VIF_j = \ frac {1} {1-R {^ 2} _j}$$

この式では $$$R {^ 2} _j$ -間の相互決定係数 $$$X_j$ およびその他の要因。 VIFの少なくとも1つが> 10である場合、多重共線性の存在を仮定するのが合理的です。

上記のすべての条件を順守することが私たちにとってなぜ重要なのですか？ 全体のポイントはガウス・マルコフの定理であり 、これによれば、これらの制限が守られた場合にのみ最小二乗推定が正確で効果的です。

これらの制限を克服する方法

1つ以上の制限の違反は、まだ文章ではありません。

1. 回帰の非線形性は、変数の変換、たとえば自然対数ln
   
   
   
   関数によって克服できます。
2. 同様に、従属変数のln
   
   
   
   またはsqrt
   
   
   
   変換を使用するか、重み付き最小二乗法を使用して、不均一な分散の問題を解決することができます。
3. 多重共線性の問題を排除するために、変数を排除する方法が使用されます。 その本質は、 高度に相関した説明変数が回帰から削除され、再評価されることです。 除外する変数の選択基準は、相関係数です。 この問題を解決する別の方法があります。それは、多重共線性によって特徴付けられる変数、それらの線形結合を置き換えることです 。 これは完全なリストではなく、 段階的な回帰やその他の方法がまだあります。

残念ながら、線形回帰の条件と欠陥のすべての違反が自然対数を使用して排除できるわけではありません。 たとえば、外乱の自己相関が発生する場合は、1つ下に戻り、より適切な新しいモデルを構築することをお勧めします。

Habréのプラスの線形回帰

したがって、非常に理論的な荷物であり、モデル自体を構築できます。

長い間、私はその緑色の数字が何に依存しているかに興味がありました。これは、Habréの投稿の評価を示しています。 自分の投稿の利用可能な統計をすべて収集したので、線形回帰モデルで実行することにしました。

tsv



ファイルからデータをロードします。

 > hist <- read.table("~/habr_hist.txt", header=TRUE) > hist
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 points reads comm faves fb bytes 31 11937 29 19 13 10265 93 34122 71 98 74 14995 32 12153 12 147 17 22476 30 16867 35 30 22 9571 27 13851 21 52 46 18824 12 16571 44 149 35 9972 18 9651 16 86 49 11370 59 29610 82 29 333 10131 26 8605 25 65 11 13050 20 11266 14 48 8 9884 ...
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

• ポイント -記事の評価
• 読み取り -ビューの数。
• comm-コメントの数。
• faves-ブックマークに追加されました。
• fb-ソーシャルネットワークで共有（fb + vk）。
• バイト - バイト単位の長さ。

多重共線性の検証。

 > cor(hist) points reads comm faves fb bytes points 1.0000000 0.5641858 0.61489369 0.24104452 0.61696653 0.19502379 reads 0.5641858 1.0000000 0.54785197 0.57451189 0.57092464 0.24359202 comm 0.6148937 0.5478520 1.00000000 -0.01511207 0.51551030 0.08829029 faves 0.2410445 0.5745119 -0.01511207 1.00000000 0.23659894 0.14583018 fb 0.6169665 0.5709246 0.51551030 0.23659894 1.00000000 0.06782256 bytes 0.1950238 0.2435920 0.08829029 0.14583018 0.06782256 1.00000000
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

私の期待に反して、 最大の利益は記事が閲覧された回数からではなく、 ソーシャルネットワーク上のコメントや出版物からです 。 また、ビューとコメントの数はより強い相関関係があると考えていましたが、依存関係はかなり緩やかであり、独立変数を除外する必要はありません。

モデル自体は、 lm



関数を使用します。

 regmodel <- lm(points ~., data = hist) summary(regmodel) Call: lm(formula = points ~ ., data = hist) Residuals: Min 1Q Median 3Q Max -26.920 -9.517 -0.559 7.276 52.851 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 1.029e+01 7.198e+00 1.430 0.1608 reads 8.832e-05 3.158e-04 0.280 0.7812 comm 1.356e-01 5.218e-02 2.598 0.0131 * faves 2.740e-02 3.492e-02 0.785 0.4374 fb 1.162e-01 4.691e-02 2.476 0.0177 * bytes 3.960e-04 4.219e-04 0.939 0.3537 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 16.65 on 39 degrees of freedom Multiple R-squared: 0.5384, Adjusted R-squared: 0.4792 F-statistic: 9.099 on 5 and 39 DF, p-value: 8.476e-06
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最初の行では、線形回帰のパラメーターを設定します。 文字列points ~.



従属変数points



と他のすべての変数を回帰変数として定義します。 points ~ reads



、変数のセット- points ~ reads + comm



を使用して、1つの独立変数を定義できます。

次に、結果の解読に進みます。

• Intercept
  
  
  
  -モデルが次の形式で表示される場合 $$$\ beta_0 + \ beta_1 * x + \イプシロン$ それから $$$\ beta_0$ -線と座標軸の交点、またはintercept
  
  
  
  。
• R-squared
  
  
  
  決定係数は、回帰因子と従属変数の関係がどれだけ近いかを示します。これは、説明されていない外乱に対する説明された外乱の和の比率です。 1に近いほど、依存性が顕著になります。
• Adjusted R-squared
  
  
  
  -問題 $$$R ^ 2$ 何らかの方法で因子の数とともに増加するため、モデルに多くの因子がある場合、この係数の高い値は欺くことができます。 相関
  
  
  
  からこのプロパティを削除するために
  
  
  
  が発明されました。
• F-statistic
  
  
  
  -回帰モデル全体の有意性を評価するために使用され、説明不可能な分散に対する説明可能な分散の比率です。 線形回帰モデルが正常に構築された場合、分散の重要な部分を説明し、分母に小さな部分を残します。 パラメータの値が大きいほど、優れています。
• t value



t
  
  
  
  基づく基準。 線形回帰のパラメーターの値は、因子の有意性を示します; t > 2
  
  
  
  因子はモデルにとって有意であると見なされます。
• p value
  
  
  
  -これは、独立変数が従属変数のダイナミクスを説明しないことを示す、帰無仮説の真理の確率です。 p value
  
  
  
  しきい値レベル（最も要求の厳しいレベルでは.05または.01）を下回っている場合、仮説ゼロは偽です。 低いほど良い 。

$$

$$F = \ frac {RSS *（m-1）} {ESS *（n-m）} = \ frac {R ^ 2} {1-R ^ 2} * \ frac {m-1} {n-m}$$

ソーシャルネットワーク上のコメントや投稿などの非線形要因を平滑化することで、モデルを少し改善することができます。 変数fb



とcomm



の値comm



それらの累乗で置き換えます。

 > hist$fb = hist$fb^(4/7) > hist$comm = hist$comm^(2/3)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

線形回帰パラメーターの値を確認します。

 > regmodel <- lm(points ~., data = hist) > summary(regmodel) Call: lm(formula = points ~ ., data = hist) Residuals: Min 1Q Median 3Q Max -22.972 -11.362 -0.603 7.977 49.549 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.823e+00 7.305e+00 0.387 0.70123 reads -6.278e-05 3.227e-04 -0.195 0.84674 comm 1.010e+00 3.436e-01 2.938 0.00552 ** faves 2.753e-02 3.421e-02 0.805 0.42585 fb 1.601e+00 5.575e-01 2.872 0.00657 ** bytes 2.688e-04 4.108e-04 0.654 0.51677 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 16.21 on 39 degrees of freedom Multiple R-squared: 0.5624, Adjusted R-squared: 0.5062 F-statistic: 10.02 on 5 and 39 DF, p-value: 3.186e-06
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ご覧のとおり、モデルの全体的な応答性が向上し、パラメーターが強化されました より絹のようになりました 、 F-



が増加し、



れた



も増加しました。

線形回帰モデルの適用性の条件が満たされているかどうかを確認しますか？ Darbin-Watsonテストは、外乱の自己相関をチェックします。

 > dwtest(hist$points ~., data = hist) Durbin-Watson test data: hist$points ~ . DW = 1.585, p-value = 0.07078 alternative hypothesis: true autocorrelation is greater than 0
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最後に、Broysch-Paganテストを使用して分散の不均一性をチェックします。

 > bptest(hist$points ~., data = hist) studentized Breusch-Pagan test data: hist$points ~ . BP = 6.5315, df = 5, p-value = 0.2579
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結論として

もちろん、Habra-Topics評価の線形回帰モデルは、最も成功しているわけではありませんでした。 データのばらつきの半分以下を説明できました。 自己相関も明確ではないため、不均一な分散を取り除くために要因を修復する必要があります。 一般に、深刻な評価に十分なデータはありません。

しかし一方で、それは良いことです。 さもなければ、Habrで急いで書かれたトロール投稿は自動的に高い評価を獲得しますが、幸いなことにそうではありません。

使用材料

1. 回帰分析およびプロット解釈の初心者向けガイド
2. 相関および回帰分析の方法
3. Kobzar A.I.数学統計を適用しました。 -M。：Fizmatlit、2006年。
4. ウィリアムH.グリーン計量経済分析