UMAP(Uniform Manifold Approximation and Projection)は、新しい次元削減アルゴリズムであり、実装が最近リリースされたライブラリです。 アルゴリズムの作成者は、 UMAPが次元削減の最新モデル、特にt-SNEに挑戦できると信じています。 彼らの研究結果によると、UMAPは元の特徴空間の次元に制限を持たず、これは削減する必要があり、t-SNEよりもはるかに高速で計算効率が高く、グローバルデータ構造を新しい縮小された空間に転送するタスクによりよく対応します。
この記事では、UMAPとは何か、アルゴリズムを構成する方法を理解し、最後にtMAPが実際にt-SNEより優れているかどうかを確認します。

理論のビット
次元削減アルゴリズムは、2つの主要なグループに分けることができます。グローバルデータ構造またはポイント間のローカル距離のいずれかを維持しようとします。 前者にはPrincipal Component Method(PCA)やMDS(Multidimensional Scaling)などのアルゴリズムが含まれ、後者にはt-SNE 、 ISOMAP 、 LargeVisなどが含まれます。 UMAPは特に後者を指し、t-SNEと同様の結果を示します。
アルゴリズムの原理を深く理解するには、強力な数学的訓練、リーマン幾何学およびトポロジーの知識が必要であるため、2つの主要なステップに分けられるUMAPモデルの一般的な考え方のみを説明します。 最初の段階では、仮定によりデータが配置されているスペースを評価します。 先験的に設定することができます )、またはデータに基づいて評価します。 そして、2番目のステップでは、最初の段階で推定された空間から新しい、より小さな次元へのマッピングを作成しようとしています。
応募結果
それでは、UMAPをいくつかのデータセットに適用し、その視覚化品質をt-SNEと比較してみましょう。 私たちの選択は、Tシャツ、ズボン、セーター、ドレス、スニーカーなどの10のクラスのさまざまな衣服の70,000枚の白黒画像を含むFashion MNISTデータセットに基づいています。 各画像のサイズは28x28ピクセルまたは合計784ピクセルです。 これらはモデルの機能になります。
それでは、PythonでUMAPライブラリを使用して、衣服を2次元平面上に表示してみましょう。 近隣の数を5に設定し、残りのパラメーターはデフォルトのままにします。 それらについては後ほど説明します。
import pandas as pd import umap fmnist = pd.read_csv('fashion-mnist.csv') # embedding = umap.UMAP(n_neighbors=5).fit_transform(fmnist.drop('label', axis=1)) #
変換の結果、元のデータセットと同じ長さの2つのベクトルが生成されました。 これらのベクトルを視覚化し、アルゴリズムがデータ構造をどのように保存しているかを確認します。
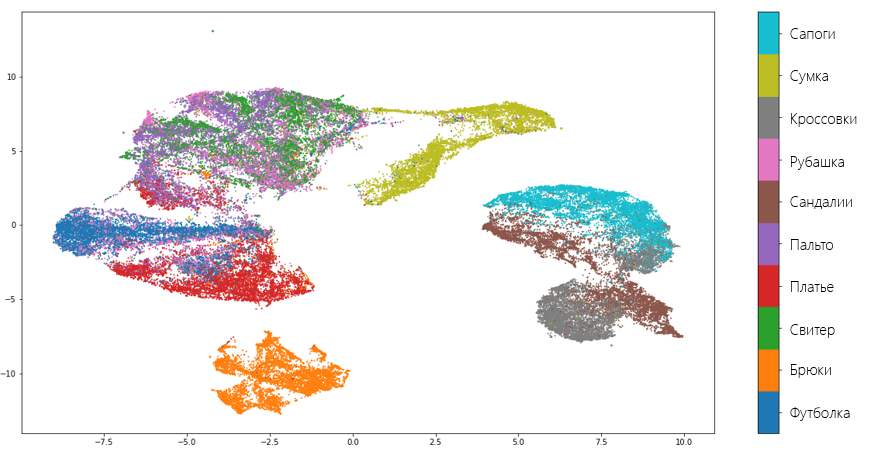
ご覧のように、このアルゴリズムは非常にうまく機能し、あるタイプの衣服と別のタイプの衣服を区別する貴重な情報のほとんどを「失わなかった」。 また、アルゴリズムの品質は、UMAPが靴、胴体、およびズボンを互いに分離し、これらが完全に異なるものであることを認識しているという事実によっても証明されています。 もちろん、間違いもあります。 たとえば、モデルはシャツとセーターは同じものであると判断しました。
次に、同じデータセットを使用してt-SNEを管理する方法を見てみましょう。 これを行うには、 マルチコアTSNEを使用します。これは、アルゴリズムのすべての実装の中で最速(シングルコアモードでも)です。
from MulticoreTSNE import MulticoreTSNE as TSNE tsne = TSNE() embedding_tsne = tsne.fit_transform(fmnist.drop('label', axis = 1))
結果:
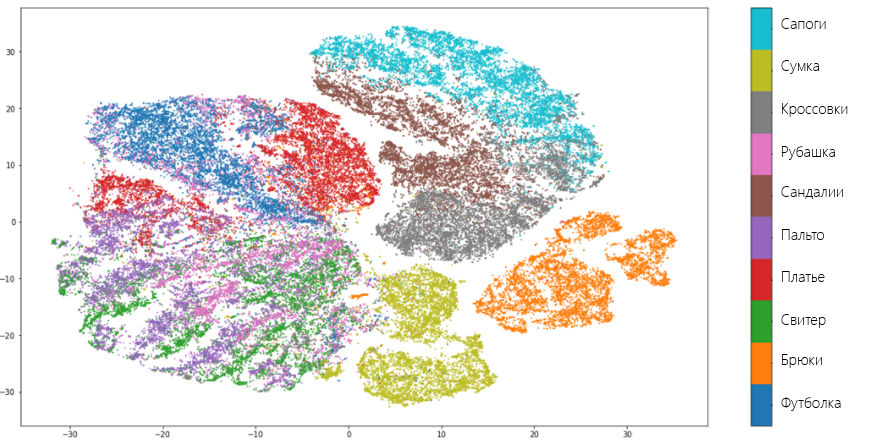
T-SNEはUMAPと同様の結果を示し、同じ間違いを犯します。 ただし、UMAPとは異なり、t-SNEはズボン、胴体と脚の物が互いに近接しているため、別々のグループで衣類のタイプを明確に統一していません。 しかし、一般的に、両方のアルゴリズムはタスクに等しくうまく対応しており、研究者はどちらかを選択して自由に選択できます。 それは、1人の「しかし」ではなかったかもしれません。
この「しかし」は学習の速度です。 4つのIntel Xeon E5-2690v3コア、2.6 Hz、サイズ70000x784のデータセット上の16 GBのRAMを搭載したサーバーでは、UMAPは4分21秒で学習しましたが、t-SNEはほぼ5倍の時間がかかりました: 20分、14秒 。 つまり、UMAPは計算効率がはるかに高く、t-SNEを含む他のアルゴリズムよりも大きな利点があります。
アルゴリズムパラメーター
近隣の数はn_neighborsです。 このパラメーターを変更することで、データの新しい空間表現に保存するより重要なもの(グローバルまたはローカルデータ構造)を選択できます。 パラメーターの値が小さいということは、データが分布している空間を推定しようとすると、アルゴリズムは各点の周りの小さな近傍に制限されることを意味します。つまり、ローカルデータ構造をキャプチャしようとします(おそらく全体的な画像を損なう)。 一方、 n_neighborsの値が大きいと、UMAPはより大きな近傍のポイントを考慮し、グローバルデータ構造を保持しますが、詳細は失われます。
n_neighborsパラメーターがトレーニングの品質と速度にどのように影響するかを示すデータセットの例を見てみましょう。
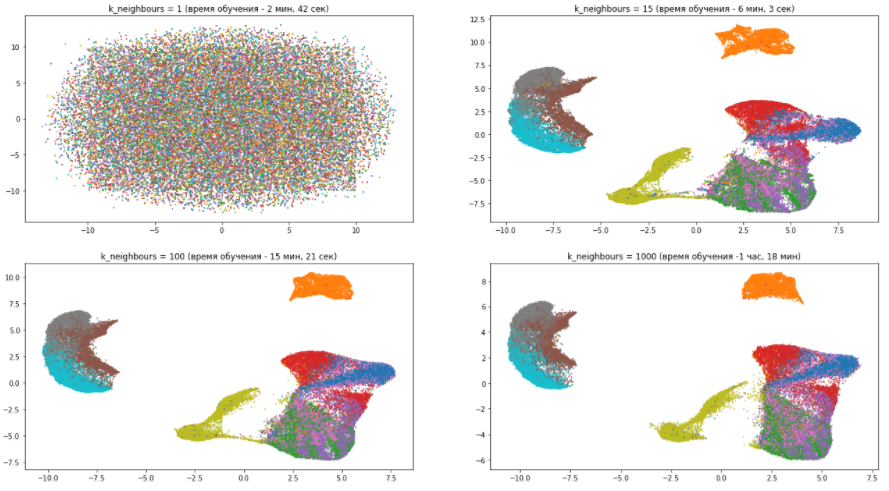
この図から、次のいくつかの結論を引き出すことができます。
- 近傍の数が1に等しい場合、アルゴリズムは詳細に集中しすぎて、一般的なデータ構造を簡単に捕捉できないため、アルゴリズムはひどく動作します。
- 隣人の数が増えると、モデルは異なるタイプの服の違いにますます注意を払わなくなり、似たような服をグループ化して混ぜ合わせます。 同時に、全く異なるワードローブアイテムがさらに離れています。 すでに述べたように、全体像はより明確になり、詳細はぼやけています。
- n_neighborsパラメーターは、トレーニング時間に大きく影響します。 したがって、慎重に選択する必要があります。
最小距離はmin_distです。 このパラメーターは、文字どおりに解釈する必要があります。新しいスペース内のポイントの最小距離を決定します。 データがどのクラスターに分割されているかに関心がある場合は低い値を使用し、データ構造全体を確認することがより重要な場合は高い値を使用する必要があります。
データセットに戻って、 min_distパラメーターの効果を評価しましょう。 n_neighbors値は固定され、5に等しくなります。
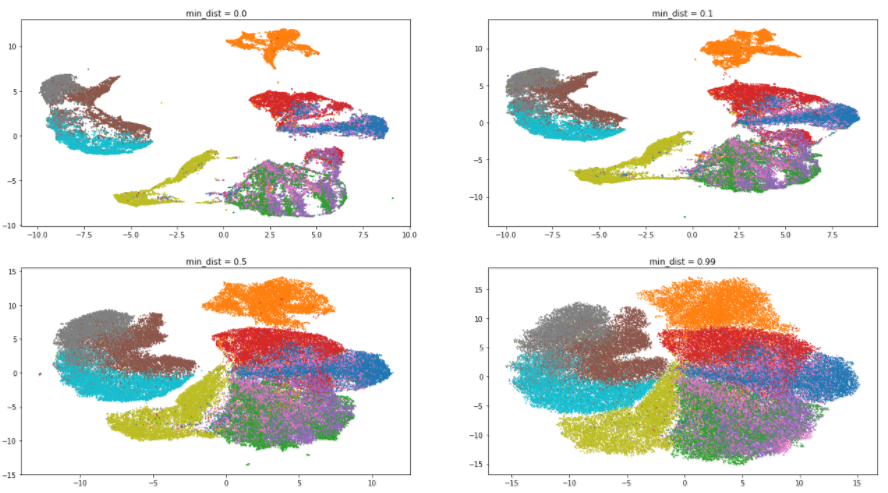
予想どおり、パラメーター値を大きくすると、クラスター化の度合いが低くなり、データがヒープに収集され、それらの差が消去されます。 興味深いことに、 min_distの最小値を使用して、アルゴリズムはクラスター内の違いを見つけ、それらをさらに小さなグループに分割しようとします。
距離メトリックはmetricです。 メトリックパラメーターは、ソースデータ空間での距離の計算方法を決定します。 デフォルトでは、UMAPはミンコフスキーからハミングまで、あらゆる種類の距離をサポートしています。 メトリックの選択は、このデータとそのタイプの解釈方法によって異なります。 たとえば、テキスト情報を操作する場合は、コサイン距離( metric = 'cosine' )を使用することをお勧めします。
データセットを引き続き使用して、さまざまなメトリックを試してみましょう。
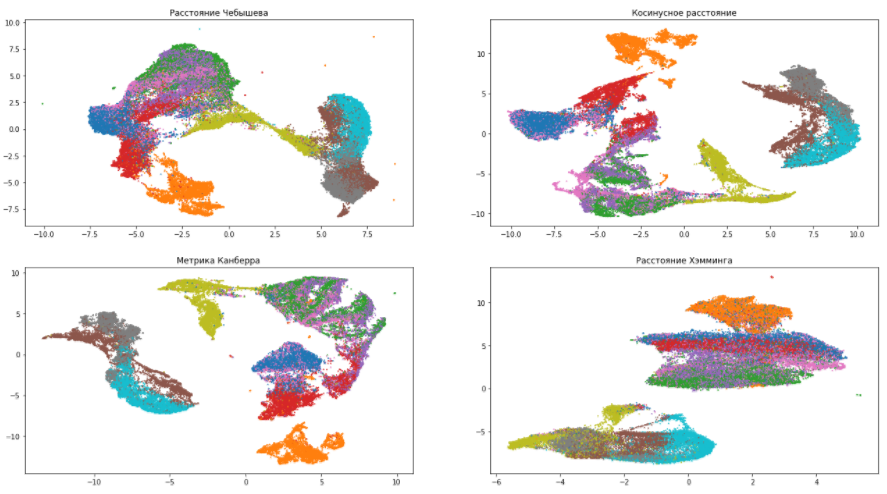
これらの写真によると、距離の尺度の選択が最終結果に非常に大きな影響を与えることを確認できます。したがって、その選択に責任を持ってアプローチする必要があります。 多様性の中からどのメトリックを選択すべきかわからない場合は、ユークリッド距離が最も安全なオプションです(デフォルトではUMAPにあります)。
有限空間の次元はn_componentsです。 ここではすべてが明らかです。パラメーターは、結果のスペースの次元を決定します。 データを視覚化する必要がある場合は、2または3を選択する必要があります。変換されたベクトルを機械学習モデルの機能として使用すると、さらに多くのことができます。
おわりに
UMAPはごく最近開発され、絶えず改善されていますが、作業の質の点で他のアルゴリズムに劣ることはなく、最終的に次元の減少という現代のモデルの主要な問題であるスローラーニングを解決できると言えます。
最後に、300万の単語ベクトルのGoogleニュースデータセットをUMAPがどのように視覚化できたかをご覧ください。 トレーニング時間は200分でしたが、t-SNEには数日かかりました。

ところで、図面はビッグデータを視覚化するためのデータシェーダーライブラリを使用して作成されました。これについては、次の記事のいずれかで説明します。
次元削減アルゴリズムにはSVDがあります。SVDは、3月22日に開始されるプログラム"Big Data Specialist 8.0"で推奨事項を作成する際に注意を払っています。