むかしむかし、すばらしいMatlabプログラムを書いた賢くて貪欲な人たちがいました。 彼らはお金がとても好きだったので、プログラムが良くて貪欲になったので、彼らは賢明でした。 彼らはそれを非常に愛し、お金を稼いだ真面目なおじさんたちからだけでなく、時々乾いたパンを買うことができなかった貧しい学生たちからもMatlabのためにそれを取りました。 そしておとぎ話はすぐに悲しいことに終わります。もし世界にmatlabに似たプログラムを書く親切で頭のいい人がいなければ、少なくとも何らかの形で働いていますが、それを望むすべての人にとっては無料です。 そしてオープンソース。 それで、貧しい学生自身がそれらのプログラムを追加し始め、彼らは毎年より良く働き始めました。 そして、彼らは皆、生き、生き、そして善を始めました...
はじめに
ほとんどの科学者は、数値法が内部にどのように配置されているかについて困惑していません。 彼らは単にそれらを使用し、仕事で数値計算の専用パッケージを使用します。 これは、これらのメソッドがどのように機能するかを理解する必要がないという意味ではありません。 人はプログラムを作成しますが、それは彼にとって間違いです。 また、最も高価で洗練された数値数学のシステムでも、常にエラーが識別されます。 さらに、標準システムの使用が不可能なタスクがあります。
同時に、現代の科学者にとって普遍的な数学ソフトウェアを使用する能力は必須です。なぜなら、自転車を発明するとき、主な問題を解決することはできないからです。 今日、私たちは約束されたOctaveを検討し、次の子供たちの問題をその助けを借りて解決しようとしながら、子供っぽくない結論を出します。
1. Octaveとは何ですか?
GNU Octaveは、独自の仲間であるMatlabの概念に基づいた無料の数学数学パッケージです。 現在人気のあるすべてのデスクトッププラットフォームで使用できます。公式Webサイトのダウンロードセクションにアクセスして入手できます。
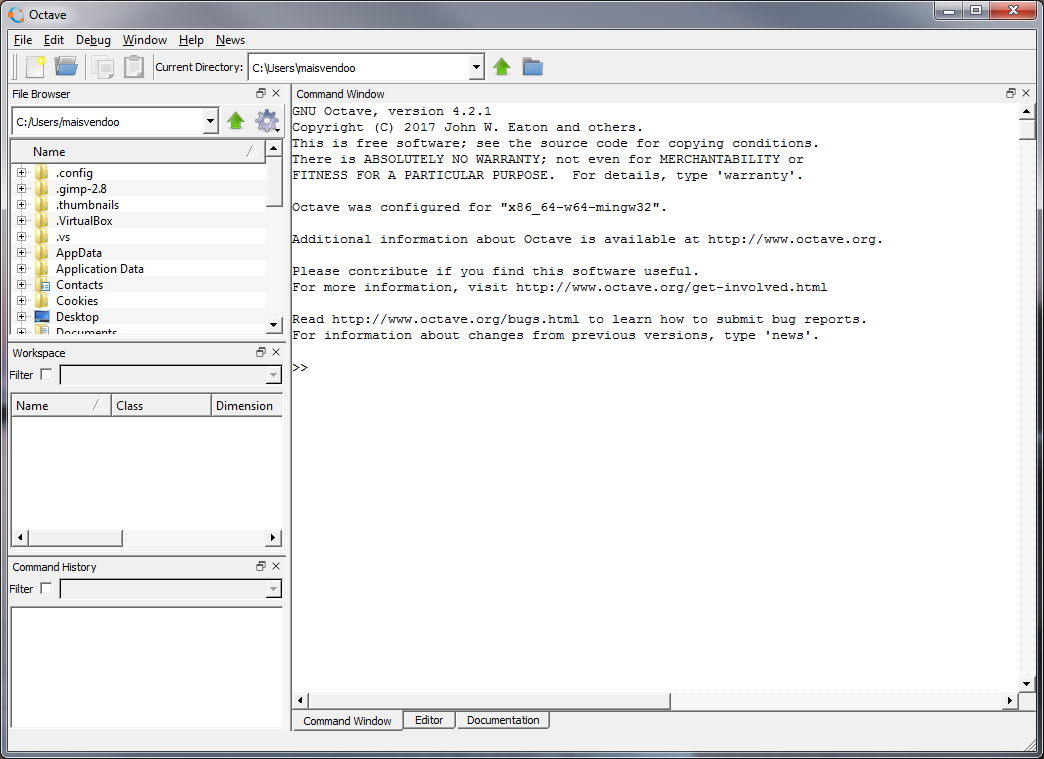
画面の大部分は、「>>」という形式のコマンドプロンプトを備えた、いわゆるコマンドウィンドウで占められています。 そこに何かを入力してEnterを押します
>> 2 + 2 ans = 4
ゴージャス、変数ansには最後の操作の結果が含まれます(結果の下に明示的に変数を入力しない限り)
>> x = 3 + 2 x = 5
変数は通訳言語で慣習的であるように、オンザフライで入力されます。 はい、実際、m言語のオクターブはインタープリターの言語であり、類似の言語マトラバを非常に連想させます。 いったん巻き上げられると、変数は次の割り当てまで、またはシェルが完全にクリアされるまで、値と型を保持します
>> x + ans ans = 9
ウィンドウの左側には、それらが配置されている領域(上から下)があります。ファイルマネージャー、グローバル変数のリスト、値、および入力されたコマンドの履歴
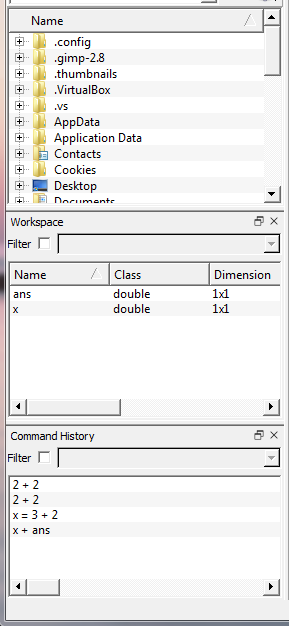
変数には次元(次元)1x1が示されているという事実に注意する価値があります。 Matlabと同様、Octaveの主なデータ型は行列です。 したがって、実際の数値は、1つの要素につき1つのサイズの行列です。
メニューから[編集]-> [ワークスペースのクリア]を選択してすべてのグローバル変数をクリアし、右クリックして[ウィンドウのクリア]を選択してコマンドウィンドウをクリアします。 変数を消去し、xを入力して取得します
>> x error: 'x' undefined near line 1 column 1 >> x = 3 x = 3 >> x x = 3
変数xが再び値を明示的に割り当てるまで、変数xは使用できなくなったことがわかります。
率直に言って、私は一度もOcatveで働いたことはなく、読者にそれを理解しています。 したがって、何らかの問題を解決するのに十分な知識をすでに持っていると仮定します。 たとえば、 前回決定したもの 。 しかし、最初に...
2.コーシーの標準形
覚えておいて、私は、狭いクラスを除いて、数値法の大部分が一次方程式のために「シャープ化」されていると言ったのですか? そして、これらの方法を方程式の解に適用する前に、次数を下げる必要がありますか? 問題は、すべての方程式が順序の縮小を認めないことです。 ただし、任意のn次方程式はn個の1次方程式に変換できます。 これは、方程式の通常のコーシー形式への変換と呼ばれます。 過去の方程式を取る
それを思い出す
それから
そして、1つの2次方程式の代わりに、同時に一緒に解く必要がある2つの1次方程式を取得します
これは単なる1つの方程式ではなく、2つの未知の依存関係を含む微分方程式系です そして 。
連立方程式を数値的に解く方法は? はい、1つの方程式と同じです。 すべての変数を列ベクトル(配列または列行列のいずれか、それを表現するのが都合が悪い場合)に集めましょう
正しい部分も列ベクトルに収集されます
その後、オイラー法の繰り返し式は、これらの列の各要素に対して有効になります
ここで、nは方程式の数です。ここでは、2つの方程式があります。
なぜ私はこれをすべて行うのですか? また、Octaveは微分方程式を通常のコーシー形式で表現する必要があるという事実。
力学の観点から、列ベクトルyはシステムの状態ベクトルまたは位相座標のベクトルと呼ばれます。 その後、方程式系は1つのベクトル方程式になります
さて、コマンドウィンドウでオクターブタイプ
>> function dydt = F(y, t)
したがって、入力で位相座標yの現在の値と現在の時間tを受け取り、出力で位相座標の導関数の値を返す関数を定義します。 コマンドプロンプト「>>」が消えていることがわかります。システムは、キーワードendfunctionを使用して関数の本体の入力が完了するまで待機します。 機能のダイヤルを続けます
>> function dydt = F(y, t) g = 10 dydt(1) = y(2) dydt(2) = -g endfunction
したがって、関数の本体で、g = 10-重力加速度の許容値を決定しました。 左側の変数リストには表示されていません。この変数はローカルであり、関数内にのみ存在します。 変数yは列行列で、yの最初の要素(1)は座標z、2番目のy(2)は速度ベクトルv zの投影です。 したがって、dydtは関数が返す値であり、列行列でもあり、その最初の要素は時間のzの導関数であり、2番目の要素は時間のv zの導関数です。 つまり、オクターブに関して微分方程式系を書き留めました。
次に、結果を取得する必要がある時間範囲を決定します。 0.1のステップで、0から1秒までの10ポイントとします-結果を手動の例と比較します
>> t0 = 0 t0 = 0 >> tend = 1 tend = 1 >> deltaT = 0.1 deltaT = 0.10000 >> t = [t0:deltaT:tend] t = 0.00000 0.10000 0.20000 0.30000 0.40000 0.50000 0.60000 0.70000 0.80000 0.90000 1.00000
ここではすべてが明らかです。t0は最初の瞬間であり、tendは最後の瞬間です。 しかし、deltaT = 0.1秒は積分ステップではありません ! これは、Ocatveが方程式の数値解を表示する間隔です。 最後のコマンドは、ソリューションを取得したい時点の配列を形成します。
最後の記事からわかるように、方程式を数値的に解くには、速度と座標の初期値を知る必要があります。 Octaveに設定する必要があります
>> y0 = [100; 0] y0 = 100 0
それにより、初期座標と速度の垂直投影の初期値を含む列行列を決定しました。 今、方程式を解きます
>> y = lsode("F", y0, t)
関数lsodeは、方程式を数値的に解きます。 最初のパラメーターは、位相座標の導関数を計算する関数の名前です。 これは関数Fです。定義しました。 2番目のパラメーターは初期条件 、つまり、時間t = t0での位相座標の値です。 最後のパラメーターは、位相座標の値を計算する時点の配列です。 Enterをクリックします...
それに応じて、山のようなトライプが落ちて、文で終わる
g = 10 dydt = -0.99690 dydt = -0.99690 -10.00000 g = 10 dydt = -0.99690 dydt = -0.99690 -10.00000 g = 10 dydt = -0.99690 dydt = -0.99690 -10.00000 g = 10 dydt = -1.9936 -- less -- (f)orward, (b)ack, (q)uit
内臓をさらにめくる(f)、戻る(b)、または出る(q)ことができます。 * nixのようなシステムを知っている人は、これがless unixユーティリティの制御下でのコンソール出力であることを知っています。 わからないふりをして、キーボードのqを押してここから出ます。
コマンドラインに「y」と入力し、Enterキーを押します
>> y y = 100.00000 0.00000 99.95000 -1.00000 99.80000 -2.00000 99.55000 -3.00000 99.20000 -4.00000 98.75000 -5.00000 98.20000 -6.00000 97.55000 -7.00000 96.80000 -8.00000 95.95000 -9.00000 95.00000 -10.00000
何にも似ていませんか? もちろん、これは前回の記事のタスクで得たまさにその解決策です。 今では驚くほど正確です-値は分析ソリューションと一致しています! 秘密をお伝えします-これが問題の正確な解決策です。 これは、lsode関数がオイラー法を使用して問題を解決するのではなく、より高度なものを使用するためです。 石は一定の加速度で移動し、この方法で使用される数値近似式は明らかに問題の分析解と一致します。 ただし、浮動小数点数を表すマシンの荒野に登ると、...まあ、まあ、今ではそれはポイントではありません。
3.スケジュールを作成する
今すぐコマンドを入力してください
>> plot(t, y)
ソリューションをグラフィカルに表示したウィンドウがポップアップします
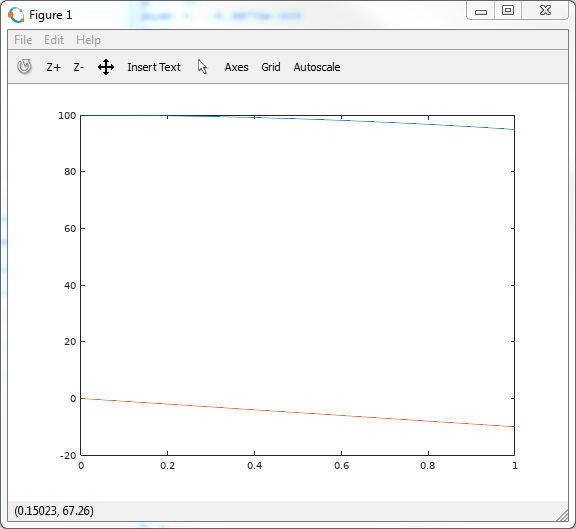
上の青い曲線は、石の座標です。 下のオレンジは、速度の垂直投影です。 入力したコマンドは、すべての機能のグラフを一度に作成するという点で不便です。 そして、構築したい場合、速度の高さへの依存性は? それからそうします
>> plot(y(:,1), y(:,2))
y(1)変数が横座標に沿って移動し、y(2)が縦座標に沿って移動するグラフが作成されます。縦座標は、それぞれ速度の高さと垂直投影です。
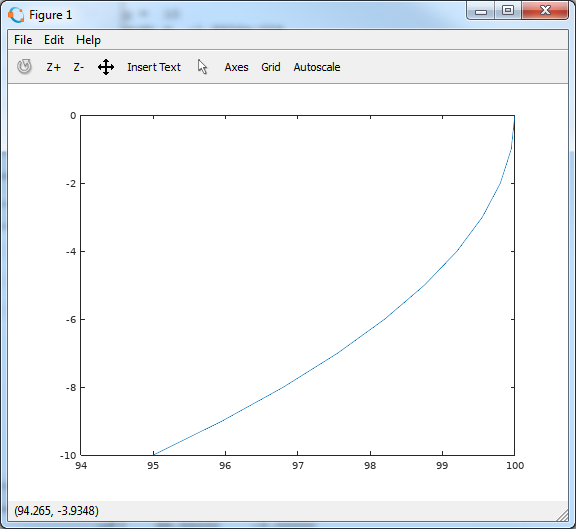
このような力学のグラフは、システムの位相ポートレート 、つまり位相座標の空間におけるシステムの軌跡と呼ばれます。 この場合、位相座標は、地球の表面上の石の高さとその速度です。 力学では、時間の関数の形で正確な解を得ることができないことがよくありますが、エネルギーの考慮に基づいて座標と速度を互いに関連付けることができます。 得られた依存関係に基づいて、システムの位相軌道を見つけ、最後まで問題を解決することなく、その運動の性質について多くの結論を引き出すことができます。 これについてもなんとか話します。
それまでは、独立したタスクを実行することを提案します。高さの時間依存性と時間依存性のグラフを別々のウィンドウで作成します。 そして、ネタバレを見ないようにしてください
答え
高さz(t)
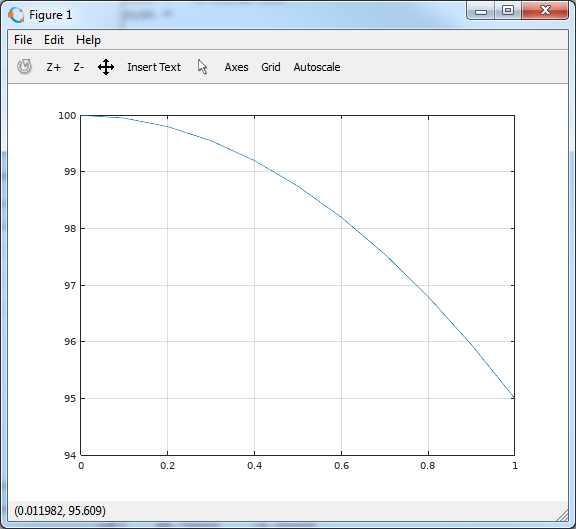
速度v z (t)
>> plot(t, y(:,1))

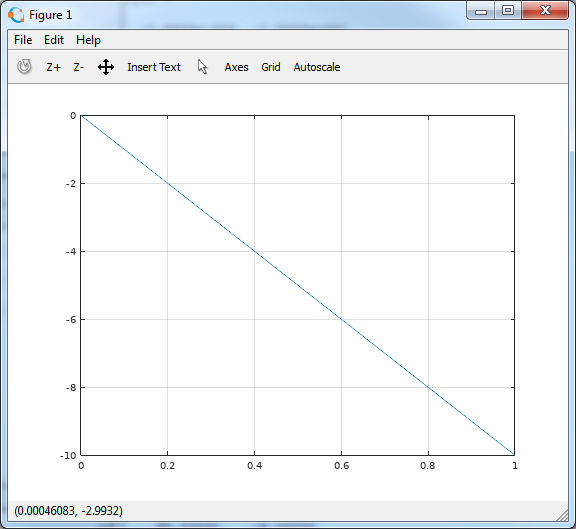
速度v z (t)
>> plot(t, y(:,2))

おわりに
これで、数値シミュレーションの媒体としてのOctaveの最初の知人は、完全であると見なされます。 これで、より洗練された知恵を理解できる強力なツールが手に入りました。
見てくれてありがとう、またね!