Clever Geek Handbook

私のお気に入りのアルゴリズム：線形時間で中央値を見つける

画像






リストの中央値を見つけることは簡単な作業のように思えるかもしれませんが、線形時間での実装には深刻なアプローチが必要です。 この投稿では、中央値の中央値を使用して決定論的な線形時間でリストの中央値を見つける、お気に入りのアルゴリズムの1つについて説明します。 このアルゴリズムが線形時間で実行されるという証明はかなり複雑ですが、投稿自体は、アルゴリズム分析に関する初期レベルの知識を持つ読者には理解できます。



O（n log n）の中央値を見つける



中央値を見つける最も簡単な方法は、リストをソートし、インデックスで中央値を選択することです。 比較による最速のソートはO(n log n)



で実行されるため、ランタイム1、2はそれに依存します。 



 def nlogn_median(l): l = sorted(l) if len(l) % 2 == 1: return l[len(l) / 2] else: return 0.5 * (l[len(l) / 2 - 1] + l[len(l) / 2])


このメソッドのコードは最もシンプルですが、間違いなく最速ではありません。



平均時間O（n）の中央値を見つける



次のステップは、運がよければ、線形時間の平均値の中央値を見つけることです。 「quickselect」と呼ばれるこのアルゴリズムは、Tony Hoarによって開発されました。TonyHoarは、同様の名前のソートアルゴリズム-quicksortを発明しました。 これは再帰的なアルゴリズムであり、（中央値だけでなく）任意の要素を見つけることができます。



  1. リストのインデックスを選択します。 選択方法は重要ではありませんが、実際にはランダムも非常に適しています。 このインデックスを持つ要素はピボットと呼ばれます。
  2. リストを2つのグループに分割します。

    1. ピボット以下の要素、 lesser_els



    2. 要素は、ピボット、 great_els



      よりも厳密に大きい
  3. これらのグループの1つに中央値が含まれることがわかっています。 k番目の要素を探しているとします。

    • lesser_els



      にk個以上の要素がある場合、 k lesser_els



      要素を探しlesser_els



      リストを再帰的にlesser_els



      ます。
    • lesser_els



      要素がk未満の場合greater_els



      リストを再帰的にgreater_els



      ます。 kを検索する代わりに、 k-len(lesser_els)



      を検索します。


11個の要素に対して実行されるアルゴリズムの例を次に示します。 



    .    . l = [9,1,0,2,3,4,6,8,7,10,5] len(l) == 11,             (pivot).      3.       2.      pivot: [1,0,2], [9,3,4,6,8,7,10,5]    . 6-len(left) = 3,                  : [9,3,4,6,8,7,10,5]     ,    pivot.    2,     l[2]=6     pivot: [3,4,5,6] [9,7,10]     ,   ,                : [3,4,5,6]     ,    pivot.    1,     l[1]=4     pivot: [3,4] [5,6]     ,   ,       .        : [5,6]        ,        .    ,   5. return 5


クイック選択を使用して中央値を見つけるために、クイック選択を個別の関数に分離します。 quickselect_median



関数は、目的のインデックスでquickselect



を呼び出します。 



 import random def quickselect_median(l, pivot_fn=random.choice): if len(l) % 2 == 1: return quickselect(l, len(l) / 2, pivot_fn) else: return 0.5 * (quickselect(l, len(l) / 2 - 1, pivot_fn) + quickselect(l, len(l) / 2, pivot_fn)) def quickselect(l, k, pivot_fn): """  k-    l (  ) :param l:    :param k:  :param pivot_fn:   pivot,     :return: k-  l """ if len(l) == 1: assert k == 0 return l[0] pivot = pivot_fn(l) lows = [el for el in l if el < pivot] highs = [el for el in l if el > pivot] pivots = [el for el in l if el == pivot] if k < len(lows): return quickselect(lows, k, pivot_fn) elif k < len(lows) + len(pivots): #       return pivots[0] else: return quickselect(highs, k - len(lows) - len(pivots), pivot_fn)


現実の世界では、Quickselectは非常に優れたパフォーマンスを発揮します。余分なリソースをほとんど消費せず、 O(n)



で平均して実行されます。 それを証明しましょう。



平均時間の証明O（n）



平均して、ピボットはリストを2つのほぼ等しい部分に分割します。 したがって、後続の各再帰は、前のステップの1⁄2 のデータで動作します。







C=n+ fracn2+ fracn4+ fracn8+...=2n=O（n）







このシリーズが2nに収束することを証明する方法はたくさんあります。 ここでそれらを引用する代わりに、この無限のシリーズに関する素晴らしいウィキペディアの記事を参照します。



Quickselectは直線的な速度を提供しますが、平均的な場合のみです。 平均に満足しておらず、線形時間でアルゴリズムの実行を保証したい場合はどうなりますか？



確定的O（n）



前のセクションでは、 平均速度O(n)



アルゴリズムであるquickselectについて説明しました。 このコンテキストでの「平均」とは、平均して、アルゴリズムがO(n)



実行されることを意味します。 技術的な観点からは、非常に不運かもしれません。各ステップで最大の要素をピボットとして選択できます。 各段階で、リストから1つの要素を取り除くことができ、その結果、 O(n^2)



ではなく、速度O(n^2)



得られます。



これを念頭に置いて、 サポート要素を選択するアルゴリズムが必要です。 目標は線形時間でピボットを選択することです。これにより、最悪の場合、quickselectで使用したときにO(n)



速度を確保するのに十分な要素が削除されます。 このアルゴリズムは、1973年にBlum、Floyd、Pratt、Rivest、Tarjanによって開発されました。 説明が不十分な場合は、 1973年の記事をご覧ください 。 アルゴリズムを説明する代わりに、Pythonでの実装について詳しくコメントします。 



 def pick_pivot(l): """   pivot    l      O(n). """ assert len(l) > 0 #   < 5,    if len(l) < 5: #           . #            ,   #          # . return nlogn_median(l) #   l    5 . O(n) chunks = chunked(l, 5) #       ,    . O(n) full_chunks = [chunk for chunk in chunks if len(chunk) == 5] #     .     ,    #   .     n/5 ,   #  O(n) sorted_groups = [sorted(chunk) for chunk in full_chunks] #      2 medians = [chunk[2] for chunk in sorted_groups] # ,   ,    ,   #       O(n). #      n/5,     O(n) #      pick_pivot    pivot  # quickselect. O(n) median_of_medians = quickselect_median(medians, pick_pivot) return median_of_medians def chunked(l, chunk_size): """  `l`    `chunk_size`.""" return [l[i:i + chunk_size] for i in range(0, len(l), chunk_size)]


中央値の中央値が良いピボットであることを証明しましょう。 サポート要素を選択するためのアルゴリズムの視覚化を提示すると役立ちます。









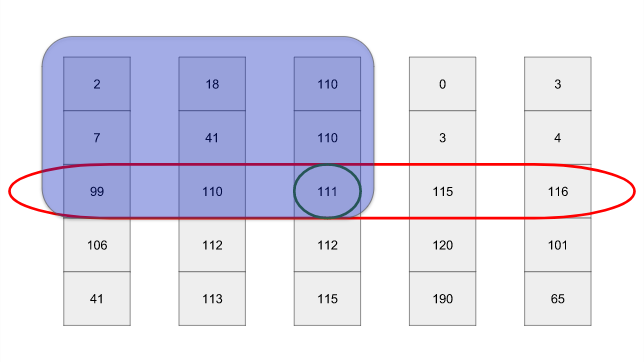
赤い楕円形は、破片の中央値、および中央の円-中央値の中央値を示します。 ピボットがリストをできるだけ均等に分割することを忘れないでください。 最悪の場合、青い長方形（左上）の各要素はピボット以下になります。 右上の長方形には、 3/5*1/2=3/10



半分の行（ 3/5*1/2=3/10



ます。 したがって、各段階で少なくとも30％の行を取り除きます。



しかし、各段階で要素の30％を破棄するだけで十分ですか？ 各段階で、アルゴリズムは次のことを行う必要があります。





その結果、合計実行時間T(n)



について次の式が得られます。







T（n）=T（ fracn5）+7T（ fracn10）+n







これがO(n)



等しい理由を証明するのはそれほど簡単ではありません。 簡単な解決策は、 基本的な再帰関係定理に依存することです。 定理の3番目のケースでは、各レベルでの作業がサブタスクの作業を支配します。 この場合、全体の作業は各​​レベルでの作業、つまりO(n)



と単純に等しくなります。



まとめると



適度に優れた参照要素がある場合、線形時間で中央値を見つけるアルゴリズムであるquickselectがあります。 中央値中央値アルゴリズム、参照要素を選択するためのO(n)



アルゴリズムがあります（quickselectには十分です）。 それらを組み合わせることで、線形時間で中央値（またはリストのn番目の要素）を見つけるためのアルゴリズムを得ました！



実際の線形時間中央値



現実の世界では、中央値のランダムな選択でほぼ常に十分です。 中央値と中央値のアプローチは線形時間で実行されますが、実際には計算に時間がかかりすぎます。 標準C++



は、 introselectと呼ばれるアルゴリズムを使用します。このアルゴリズムは、heapselectとquickselectの組み合わせを使用します。 実行制限はO(n log n)



です。 Introselectを使用すると、実際には低速ですが、上限が適切なアルゴリズムと組み合わせて、通常は上限の悪い高速アルゴリズムを使用できます。 実装は高速なアルゴリズムから始まりますが、効果的なサポート要素を選択できない場合は、より遅いアルゴリズムに戻ります。



結論として、各実装で使用される要素を比較します。 これは実行速度ではなく、quickselect関数が考慮する要素の総数です。 これは、中央値の中央値を計算する作業を考慮していません。



画像






これは私たちが期待したものです！ 決定論的なサポート要素は、ほとんどの場合、クイック選択ではランダム要素よりも少ない要素を考慮します。 幸運にも時々、最初の試行でピボットを推測します。これは緑の線のくぼみとして現れます。 数学はうまくいきます！





  1. それぞれが2 32未満の整数のリストで中央値を見つける必要がある場合、これは基数ソートの興味深いアプリケーションになります。
  2. Pythonは実際に、理論的な限界と実用的な速度の印象的な組み合わせであるティムソートを使用します。 Pythonでメモを一覧表示する 。


More articles:


All Articles