こんにちは、habrozhiteli！ 最近、Sergei Nikolenko、Arthur Kadurin、およびEkaterina Arkhangelskayaからの深層学習に関する最初のロシアの本を出版しました。 最大限の説明、最小限のコード、機械学習に関する本格的な資料、魅力的なプレゼンテーション。 次に、ニューラルネットワークのトレーニングアルゴリズムを実装するための基本概念が導入されているセクション「計算とその微分のグラフ」を検討します。
複雑な関数をより単純な関数の合成として想像できる場合、勾配降下に必要な変数に対する導関数を効率的に計算できます。 構成の形式で最も便利な表現は、計算のグラフの形式での表現です。 計算グラフは、ノードが関数（通常はかなり単純で、事前に設定されたセットから取得）であるグラフであり、エッジは関数を引数で接続します。
正式に定義するよりも、自分の目で見る方が簡単です。 写真を見てください。 2.7、同じ関数の計算の3つのグラフが表示されます。
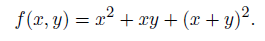
図 2.7、およびグラフは非常に簡単であることが判明しました。なぜなら、単項関数「二乗」を頂点として使用できるからです。
そして図 2.7、bグラフは少し複雑です。明示的な2乗を通常の乗算に置き換えました。 ただし、このためにサイズが増加することはありませんでした。 2.7、b、以前の計算の結果を数回再利用することが許可されており、同じxを乗算関数の入力に2回適用してその平方を計算するだけで十分です。 比較のために、図に描いた。 2.7、同じ関数のグラフで、ただし再利用なし。 今ではツリーになりますが、その中には大きなサブツリー全体を繰り返す必要があり、そこからツリーのルートへの複数のパスが一度に出て行くことができます。
ニューラルネットワークでは、計算グラフの基本的な基本関数として、ニューロンの派生元の関数が通常使用されます。 たとえば、ベクトルのスカラー積
機能を持つニューロンで構成される任意の、最も複雑なニューラルネットワークを構築するのに十分な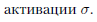 
ちなみに、加算と乗算によってスカラー積を表現することは可能ですが、ここで「細かく刻む」必要もありません：関数は初歩的であることができ、その微分と引数に対する微分を簡単に計算できます。 特に、セクション3.3で詳細に説明するニューロン活性化関数は完璧です。
そのため、非常に複雑な動作であっても、多くの数学関数は計算グラフの形式で表現でき、ノードには基本関数が含まれ、そこからレンガのように計算したい複雑な構成が得られることがわかりました。 実際、このようなグラフの助けを借りて、あまり豊富でない基本関数のセットがあっても、任意の関数を任意に正確に近似できます。 これについては少し後で説明します。
次に、主なテーマである機械学習に戻ります。 既にわかっているように、機械学習の目標は、データを最もよく説明するようにモデルを選択することです（ほとんどの場合、ここではパラメーター形式で指定されたモデルの重みを意味します）。 ここでの「ベスト」とは、原則として、エラー関数の最適化を意味します。 通常、これはトレーニングサンプル（尤度関数）と正則化関数（アプリオリ分布）の実際のエラーで構成されていますが、上から与えられたかなり複雑な関数があると単純に仮定するのに十分であり、それを最小化する必要があります。 すでに知っているように、複雑な関数を最適化するための最も単純で最も普遍的な方法の1つは勾配降下です。 また、最近、複雑な関数を定義するための最も単純で最も普遍的な方法の1つが計算のグラフであることを発見しました。
勾配降下と計算のグラフは文字通りお互いに作成されていることがわかります！ おそらくあなたが学校で教えられたように（学校のカリキュラムには一般に多くの予想外に深く興味深いものが含まれています）、機能の構成の導関数を計算するために値）、そのコンポーネントの導関数を計算することができれば十分です：
ルールは各コンポーネントに個別に適用され、結果が出ます
再び非常に期待：
このような偏微分行列はヤコビ行列と呼ばれ、その行列式は
ヤコビアン; 彼らは私たちに何度も会います。 これで、ベクトル関数を含む関数の任意の構成の導関数と勾配を計算できます。そのためには、各コンポーネントの導関数を計算できる必要があります。 グラフについては、この事実はすべてシンプルだが非常に強力なアイデアに帰着します。計算のグラフを知っていて、各ノードで導関数をとる方法を知っていれば、これはグラフが定義する複雑な関数全体の導関数をとるのに十分です！
最初に例を使用してこれを分析します。図に示したのと同じ計算グラフを考えてみましょう。 2.7。 図 2.8、およびグラフを構成する基本関数が示されています。 グラフの各ノードをaからfまでの新しい文字でマークし、入力ごとに各ノードの偏導関数を書きました。
これで偏微分を計算できます
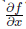図に示すように。 2.8、b：グラフのソースから導関数の計算を開始し、組成微分式を使用して次の導関数を計算します。 例：
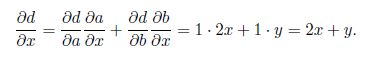
しかし、図に示すように、反対方向に進むことができます。 2.8、c。 この場合、ソースから開始します。ここでは、偏微分が常に立っています。
そして、複雑な関数の微分公式に従って、ノードを逆の順序で展開します。 ここで、式はまったく同じ方法で適用されます。 たとえば、最下位ノードでは次のようになります。
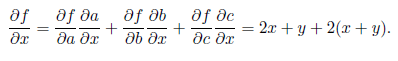
したがって、グラフ上またはソースからシンクへの組成を区別するための式を適用して、同じ変数に関する各ノードの偏微分を取得できます
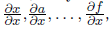排水から発生源まで、すべての中間ノードの排水の偏微分を受け取る 
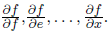もちろん、実際には、機械学習には最初のオプションではなく2番目のオプションが必要です。通常、エラー関数は同じであり、特に勾配降下を実行するすべての重みについて、一度に多くの変数に関する偏微分が必要です。
一般的に、アルゴリズムは次のとおりです。頂点が関数である方向の非周期的計算グラフG =（V、E）が与えられたと仮定します。
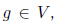、およびいくつかの頂点は入力変数x1、...、xnに対応し、入力エッジを持たず、1つの頂点は出力エッジを持たず、関数fに対応し（グラフ全体がこの関数を計算します）、エッジはノードの関数間の依存関係を示します。 次に、グラフの「最後の」頂点で関数fを取得する方法を既に知っています。このためには、エッジに沿って移動し、位相順に各関数を計算するだけで十分です。
そして、この関数の偏導関数を見つけるには、反対方向に移動するだけで十分です。 関数の偏微分に興味がある場合
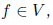上記の式に完全に従って、計算することができます 
各ノード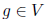 
このように：
偏微分は計算グラフのエッジとは反対の方向にカウントされるため、このアプローチは逆伝播、逆伝播、逆伝播と呼ばれます。 そして、図1のように、関数自体または1つの変数に関する導関数を計算するアルゴリズム 2.8、bは、前方伝播（fprop）アルゴリズムと呼ばれます。
最後の重要な注意事項：計算グラフ、微分、勾配などについて説明している間、実際にはニューラルネットワークについては真剣に言及していませんでした。 実際、計算のグラフに基づいて導関数/勾配を計算する方法自体は、ニューラルネットワークとはまったく関係ありません。 これは、特に実際の問題について留意するのに役立ちます。これについては、次のセクションで説明します。 実際のところ、以下で説明するディープラーニングを最大限に活用するTheanoおよびTensorFlowライブラリは、一般的に、ニューラルネットワークのトレーニング用ではなく、自動分化用のライブラリです。 それらはすべて、計算のグラフをセットアップし、並列化とビデオカードへの転送を行い、このグラフから勾配を計算することにより、効率的に処理することができます。
もちろん、これらのライブラリの上に、ニューラルネットワークの標準設計で実際にライブラリを実装できます。また、人々は常にこれを行います（以下のKerasを検討します）が、自動微分の基本的な考え方を忘れないことが重要です。 単なる標準的なニューラル構造のセットよりもはるかに柔軟で豊富であることが判明する可能性があり、ニューラルネットワークをまったく訓練しないためにTensorFlowを非常にうまく使用することがあります。
»本の詳細については、出版社のウェブサイトをご覧ください
» コンテンツ
» 抜粋
ホーカーのクーポンが20％オフ- ディープラーニング