
典型的な実装では、遺伝的アルゴリズムはいくつかの複雑な関数(記事「 遺伝的アルゴリズムの 双曲方程式。ちょうど複雑な " mrk-andreev 」または「 JavaScriptでのレーシングカーの進化 」 ilya42 )のパラメーターで動作 します 。 パラメータの数は変わらず、それらに対する操作も変更することは不可能です。これは、遺伝学が試行しないのと同じです。なぜなら、それらは私たちによって設定されているからです。
ヒューストン、問題があります
奇妙な状況が発生しました-遺伝的アルゴリズム(GA)を実際のタスクに適用する前に、まずこの問題を原理的に解決するアルゴリズムを見つけてから、遺伝的アルゴリズムを使用して最適化を試みる必要があります。 「基本」アルゴリズムの選択を間違えた場合、遺伝学は最適なものを見つけられず、エラーが何であるかを述べません。
多くの場合、そして最近では、決定論的アルゴリズムの代わりにニューラルネットワークを使用することが流行しています。 ここでは、最も幅広い選択肢(FNN、CNN、RNN、LTSMなど)もありますが、問題は同じままです。正しいものを選択する必要があります。 ウィキペディアによると、「 ネットワークの種類の選択は、問題の声明とトレーニングに利用可能なデータに基づいている必要があります 。」
もし…? GAでパラメーターを最適化せずに、このタスクに最適な別のアルゴリズムを作成する場合。 それは私が楽しみのためにしたことです。

操作からの遺伝子型
遺伝的アルゴリズムは通常、いわゆる 「遺伝子型」、「遺伝子」のベクター。 GA自体については、これらの遺伝子が何であるかは関係ありません-数字、文字、文字列、またはアミノ酸。 必ずしも交配、交配、突然変異、選択などの遺伝子型に必要な行動を観察することは重要ではありません。
したがって、「ゲノム」は基本操作であり、「遺伝子型」はこれらの操作で構成されるアルゴリズムであるという考え方です。 たとえば、数学演算で構成され、関数を実装する遺伝子型 :
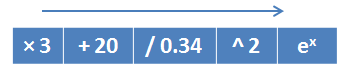
次に、GAの結果として、構造を事前に予測できない式またはアルゴリズムを取得します。
交配は実際には変化せず、新しい遺伝子型は各親からピースを受け取ります。
突然変異とは、遺伝子の1つを別の遺伝子に置き換えることです。つまり、1つの操作がアルゴリズム内で置き換えられたり、この操作のパラメーターが変更されたりします。
選択を使用すると、単純であると同時に複雑です。 アルゴリズムを作成しているので、テストする最も簡単な方法は、アルゴリズムを実行して結果を評価することです。 したがって、高速道路で進歩した自動車は、そのアーキテクチャの最適性を証明しました。 しかし、車には明確な基準がありました-彼女が運転したほど、良いです。 一般的な場合のターゲットアルゴリズムには、長さ(短いほど良い)、メモリ要件(小さいほど良い)、入力ガベージに対する耐性など、いくつかの評価基準があります。

ところで、車には1つの基準がありましたが、現在のルート内でしか機能しませんでした。 あるトラックで最高の車が別のトラックで最高になるとは考えにくい。
そして、あなたがそれについて考えたら?
どの操作を遺伝子辞書に含めるか、どのように機能させるかを考える過程で、1つの変数に対する操作に限定されるべきではないことに気付きました。 同じニューラルネットワークは、すべて(FNN)または複数(CNN)の入力変数で同時に動作するため、結果のアルゴリズムで必要な数の変数を使用する方法が必要です。 また、どの変数でどの変数が必要になるかは事前に予測できず、制限したくありません。
救助に来た...推測しないでください... フォースの言語。 より正確には、 逆ポーランドレコードと、スタックに変数の値を配置し、それらの変数に対して操作を目的の順序で実行する能力を備えたスタックマシンです。 そして括弧なし。
スタックマシンでは、算術演算に加えて、スタック演算をプログラムする必要があります- プッシュ (入力ストリームから次の値を取得してスタックに配置)、 ポップ (スタックから値を取得して結果として提供)、 dup (スタックの最上位値を複製)
やるだけ!
結果は、1つの遺伝子を実装するオブジェクトです。
生成オブジェクト
class Gen(): func = 0 param = () def __init__(self): super().__init__() self.func = random.randint(0,7) self.param = round(random.random()*2-1,2) def calc(self, value, mem): if self.func == 0: # push mem.append(value + self.param) return (None, 1) elif self.func == 1: # pop return (mem.pop() + self.param, 0) elif self.func == 2: # dup mem.append(mem[-1] + self.param) return (None, 0) elif self.func == 3: # add mem.append(mem.pop() + value + self.param) return (None, 1) elif self.func == 4: # del mem.append(mem.pop() - (value + self.param)) return (None, 1) elif self.func == 5: # mul mem.append(mem.pop() * (value + self.param)) return (None, 1) elif self.func == 6: # div mem.append(mem.pop() / (value + self.param)) return (None, 1) return (self.params, 0) def funcName(self, func): if self.func >= 0 and self.func <= 7: return [ 'push', 'pop', 'dup', 'add', 'del', 'mul', 'div', 'const'][func] return str(func) def __str__(self): return "%s:%s" % (self.funcName(self.func), str(self.param))
これは最初のオプションであり、原則として機能しますが、問題がすぐに発生しました。算術演算では値を渡す必要がありましたが、 ポップおよびdupスタックでの演算では必要ありませんでした。 呼び出し元コードで呼び出された操作を区別し、それぞれに渡すパラメーターの数を決定したくなかったので、1つの値ではなく、 値が入力値の配列を渡して、操作に必要な処理をさせました。
Gen v.2オブジェクト
class Gen(): func = 0 param = () def __init__(self): super().__init__() self.func = random.randint(0,7) self.param = round(random.random()*2-1,2) def calc(self, values, mem): if self.func == 0: # pop return mem.pop() + self.param elif self.func == 1: # push mem.append(values.pop() + self.param) return None elif self.func == 2: # dup mem.append(mem[-1] + self.param) return None elif self.func == 3: # add mem.append(mem.pop() + values.pop() + self.param) return None elif self.func == 4: # del mem.append(mem.pop() - (values.pop() + self.param)) return None elif self.func == 5: # mul mem.append(mem.pop() * (values.pop() + self.param)) return None elif self.func == 6: # div mem.append(mem.pop() / (values.pop() + self.param)) return None return self.param def funcName(self, func): if self.func >= 0 and self.func <= 7: return [ 'pop', 'push', 'dup', 'add', 'del', 'mul', 'div', 'const'][func] return str(func) def __str__(self): return "%s:%s" % (self.funcName(self.func), str(self.param))
2番目の問題は、算術演算の要求が高すぎることでした。スタック上の値と入力値の両方が必要でした。 その結果、遺伝的アルゴリズムによって単一の遺伝子型を生成することはできませんでした。 操作を、スタックを操作する操作と入力値を操作する操作に分割する必要がありました。
以下は最新バージョンです。
Gen v.8オブジェクト
class Gen(): func = 0 param = () def __init__(self, func=None): super().__init__() if func is None: funcMap = [0,1,2,3,4,5,6,7,8,9,10,11] i = random.randint(0,len(funcMap)-1) func = funcMap[i] self.func = func self.param = round((random.random()-0.5)*10,2) def calc(self, values, mem): def getVal(): v = values[0] values[0:1]=[] return v if self.func == 0: # pop return mem.pop() elif self.func == 1: # push mem.append(getVal()) return None elif self.func == 2: # dup mem.append(mem[-1] + self.param) return None elif self.func == 3: # addVal mem.append(getVal() + self.param) return None elif self.func == 4: # delVal mem.append(getVal() + self.param) return None elif self.func == 5: # mulVal mem.append(getVal() * self.param) return None elif self.func == 6: # divVal mem.append(getVal() / self.param) return None elif self.func == 7: # addMem mem.append(self.param + mem.pop()) return None elif self.func == 8: # delMem mem.append(self.param - mem.pop()) return None elif self.func == 9: # mulMem mem.append(self.param * mem.pop()) return None elif self.func == 10: # divMem mem.append(self.param / mem.pop()) return None mem.append(self.param) return None def funcName(self, func): funcNames = ( 'pop', 'push', 'dup', 'addVal', 'delVal', 'mulVal', 'divVal', 'addMem', 'delMem', 'mulMem', 'divMem', 'const') if self.func >= 0 and self.func < len(funcNames): return funcNames[func] return str(func) def __str__(self): return "%s:%s" % (self.funcName(self.func), str(round(self.param,4)))
交差アルゴリズムを選択して、遺伝子型のオブジェクトに少し手を加えなければなりませんでした。 どちらが良いか、私はまだ決めていません、私は擬似ランダム性を取っておきました。 アルゴリズム自体は__mul__乗算メソッドで定義されました。
Dnkオブジェクト
class Dnk: gen = [] level = 0 def __init__(self, genlen=10): super().__init__() self.gen = [ Gen(1), Gen(1) ] + [ Gen() for i in range(genlen-2) ] def copy(self, src): self.gen = src.gen def __mul__(self, other): divider = 2 def sel(): v = random.random()*(self.level + other.level) return v <=self.level mode = random.randint(0,3) minLen = min(len(self.gen), len(other.gen)) maxLen = max(len(self.gen), len(other.gen)) n = Dnk() if mode == 0: n.gen = [ self.gen[i] if sel() else other.gen[i] for i in range(minLen) ] elif mode == 1: n.gen = [ Gen() for i in range(minLen) ] for g in n.gen: g.param += round((random.random()-0.5)/divider,3) elif mode == 2: n.gen = [ self.gen[i-1] if i % 2 == 1 else other.gen[i] for i in range(minLen) ] for g in n.gen: g.param += round((random.random()-0.5)/divider,3) else: v = random.randint(0,1) n.gen = [ self.gen[i] if i % 2 == v else other.gen[-1-i] for i in range(minLen) ] for g in n.gen: g.param += round((random.random()-0.5)/divider,3) n.gen = n.gen + [ Gen() for i in range(minLen,maxLen) ] return n def calc(self, values): res = [] mem = [] varr = values.copy() i = 0 for g in self.gen: try: r = g.calc(varr, mem) i = i + 1 except: self.gen = self.gen[0:i] #raise break; if not r is None: res.append(r) return res def __str__(self): return '(' + ', '.join([ str(g) for g in self.gen ]) + '):'+str(round(self.level,2))
__str__メソッドは、両方のクラスの内容がコンソールにコンテンツを表示するためにオーバーライドされました。
アルゴリズムレンダリング関数はもう少し詳細です。
def calc(self, values): res = [] mem = [] varr = values.copy() i = 0 for g in self.gen: try: r = g.calc(varr, mem) i = i + 1 except: self.gen = self.gen[0:i] #raise break; if not r is None: res.append(r) return res
コメントアウトされたレイズに注意してください-最初に、誤ってクラッシュするアルゴリズムを持つ遺伝子型はこの世界に住むべきではなく、すぐに拒否されるべきだと考えていました。 しかし、過ちが多すぎて、人口が縮退していたので、オブジェクトを破壊せず、この遺伝子で切断することにしました。 そのため、遺伝子型は短くなりますが、機能し続け、その機能する遺伝子を使用できます。
そのため、遺伝子型があり、遺伝子の辞書があり、2つの遺伝子型を横断する機能があります。 以下を確認できます。
>>> a = Dnk() >>> b = Dnk() >>> c = a * b >>> print(a) (push:4.061, push:1.79, dup:-4.32, mulMem:3.6, push:-3.752, addVal:2.4, delVal:-1.863, delMem:4.06, delVal:-3.692, addMem:0.48):0 >>> print(b) (push:0.356, push:-4.8, pop:2.865, delVal:1.53, addMem:-2.853, mulVal:-1.6, const:-2.451, delVal:-2.53, divVal:4.424, delMem:-0.6):0 >>> print(c) (push:4.061, divVal:4.424, dup:-4.32, const:-2.451, push:-3.752, addMem:-2.853, delVal:-1.863, pop:2.865, delVal:-3.692, push:0.356):0 >>>
今、私たちは生殖(最高の選択と交配)と突然変異の機能が必要です。
必要な数に遺伝子型を交配および育種する機能は、3つのバージョンで記述しました。 しかし、最悪の半分はとにかく死にます。
# def mixIts(its, needCount): half = needCount // 2 its[half:needCount] = [] nIts = [] l = min(len(its), half) ll = l // 2 for ii in range(half,needCount): i0 = random.randint(0,l-1) i1 = random.randint(0,l-1) d0 = its[i0] d1 = its[i1] nd = d0 * d1 mutate(nd) its.append(nd) # def mixIts2(its, needCount): half = needCount // 2 its[half:needCount] = [] nIts = [] l = min(len(its), half) ll = l // 2 for ii in range(half,needCount): i0 = random.randint(0,ll-1) i1 = random.randint(ll,l-1) d0 = its[i0] d1 = its[i1] nd = d0 * d1 mutate(nd) its.append(nd) # def mixIts3(its, needCount): half = needCount // 2 its[half:needCount] = [] nIts = [] l = min(len(its), half) ll = l // 4 for ii in range(half,needCount): i0 = random.randint(0,ll-1) i1 = random.randint(ll,ll*2-1) d0 = its[i0] d1 = its[i1] nd = d0 * d1 mutate(nd) its.append(nd)
新しい遺伝子型に適用される突然変異関数
def mutate(it): # listMix = [ (random.randint(0,len(it.gen)-1), random.randint(0,len(it.gen)-1)) for i in range(3) ] for i in listMix: it.gen[i[0]], it.gen[i[1]] = (it.gen[i[1]], it.gen[i[0]]) # , for i in [ random.randint(0,len(it.gen)-1) for i in range(3) ]: it.gen[i] = Gen() # for i in [ random.randint(0,len(it.gen)-1) for i in range(1) ]: it.gen[i].param = it.gen[i].param + (random.random()-0.5)*2
このような遺伝的アルゴリズムはどのように適用できますか?
例:
-入力データ間のパターンを特定し、回帰分析
-信号の損失を復元し、干渉を除去するアルゴリズムを開発する-音声通信に有用
-同じチャンネルの異なるソースから来た別々の信号-音声制御に役立ち、擬似ステレオを作成します
これらのタスクには、入力値の入力配列を受け取り、同じ長さの出力値の配列を生成する遺伝子型が必要です。 適切な遺伝子型を取得して目標を達成するというタスクを組み合わせてみましたが、難しすぎることがわかりました。 初期集団の遺伝子型を選択するために遺伝学を取り除くことは簡単で、これらの遺伝子型が入力配列を処理することさえできました。
遺伝子型を選択するには、関数を作成し、遺伝子型を生成し、GAに従ってそれらを実行し、結果に従ってそれらを拒否し、生存者の配列を返します。 人口が縮退している場合、GAは前もって停止します。
# dataLen = 6 # itCount = 100 # genLen = 80 # epochCount = 100 srcData = [ i+1 for i in range(dataLen) ] def getIts(dest = 0): its = [ Dnk(genLen) for i in range(itCount) ] res = [] for epoch in range(epochCount): nIts = [] maxAchiev = 0 for it in its: try: res = it.calc(srcData) achiev = len(res) if achiev == 0: it = None continue maxAchiev = max(maxAchiev, achiev) it.level = achiev nIts.append(it) except: # print('Died',it[0],sys.exc_info()[1]) it = None its = nIts l = len(its) if l<2: print("Low it's count:",l) break; # , its.sort(key = lambda it: -it.level) if maxAchiev >= dataLen: break; mixIts(its, itCount) for it in its[:]: if it.level<dest: its.remove(it) return its
望ましい結果からの結果の偏差を評価する関数(偏差関数が大きいほど遺伝子型が悪化するため、完全なフィットネス関数ではありませんが、これは考慮されます)。
def diffData(resData, srcData): # , if len(resData) != len(srcData): return None d = 0 for i in range(len(resData)): d = d + abs((len(resData)*30 - i) * (resData[i] - srcData[i])) return d
さて、最後の仕上げは、実際には選択した遺伝子型のGAです。
# bestCount = 30 # globCount = 30000 # , seekValue = 8000 its = [] while len(its)<bestCount: its = its + getIts(len(destData)) print('Its len', len(its)) # , printIts(its[0:1], srcData) its[bestCount:len(its)]=[] for glob in range(globCount): minD = None for it in its[:]: resData = it.calc(srcData) d = diffData(resData, destData) # , . if d is None: its.remove(it) continue # it.level = 100000 - d minD = d if minD is None else min(d, minD) its.sort(key = lambda it: -it.level) if glob % 100 == 0 or glob == globCount - 1: # , 100- print('glob', glob, ':', round(minD,3) if minD else 'None', len(its)) #, resData) if minD < seekValue: print('Break') break mixIts2(its, bestCount) # printIts(its[0:3], srcData)
結果
... glob 2900 : 7067.129 18 glob 3000 : 4789.967 15 glob 3100 : 6791.239 17 glob 3200 : 6809.478 15 Break 16 0 (const:24.7735, addMem:1.7929, dup:39.1318, dup:-15.2363, mulVal:24.952, mulVal:4.7857, pop:14.4176, pop:19.8343, dup:-19.4728, pop:2.6658, dup:-14.8237, pop:6.7005, pop:1.3567, pop:-2.7399):97009.88 => [9.571, 24.952, 30.989, 35.638, 50.462, 65.698] 1 (const:24.7735, dup:-4.8988, dup:39.1318, dup:-4.3082, mulVal:24.952, mulVal:6.1096, pop:14.4176, pop:19.8343, dup:-19.4728, pop:2.6658, dup:-14.8237, pop:6.7005, pop:1.3567, pop:-2.7128):96761.03 => [12.219, 24.952, 35.226, 39.875, 54.698, 59.007] 2 (const:24.7735, addMem:1.7929, dup:39.1318, dup:-15.2363, mulVal:24.952, delVal:3.4959, pop:14.4176, pop:19.8343, dup:-19.4728, pop:2.6658, dup:-14.8237, pop:6.7005, pop:1.3567, pop:-2.7399):96276.27 => [5.496, 24.952, 30.989, 35.638, 50.462, 65.698] >>>
または、より簡単に言えば、destData = [10、20、30、40、50、60]の最適なGA結果は[9.571、24.952、30.989、35.638、50.462、65.698]でした。 この結果は、アルゴリズムによる遺伝子型によって実現されます(const:24.7735、addMem:1.7929、dup:39.1318、dup:-15.2363、mulVal:24.952、mulVal:4.7857、pop:14.4176、pop:19.8343、dup:-19.4728、pop:2.6658、dup :-14.8237、ポップ:6.7005、ポップ:1.3567、ポップ:-2.7399)。
一方では、アルゴリズムは冗長です-最終結果を取得するために不要なアクションを実行します。 一方、アルゴリズムは、6の入力ストリームから2つの値のみを使用するため、制限されています。これは、制限された入力データが原因で発生したことは明らかです。
次は?
さらに、アイデアを発展させることができます:
-結果として生じるアルゴリズムを大きなデータストリームで実行し、アルゴリズムがこのストリームに沿って最小の偏差で「通過」するほど、遺伝子型の品質が向上することがわかりました。 車との完全な類推。
-完全なForthマシンを含め、Forthテキストでアルゴリズムを生成します。 したがって、条件付き遷移とループを使用して、より複雑な計算アルゴリズムを作成できます。
-結果を得るために最も必要なもののみが残されるように、結果のアルゴリズムを分析および簡素化します。
-遺伝子の基本操作の代わりに、より複雑な操作を使用します。 たとえば、このような操作は差別化である場合があります。 または統合。 またはニューラルネットワークトレーニング。 Alan Jay Perlis氏は、辞書を拡張する必要はなく、イディオムを蓄積する必要があると言っていますが、イディオムの良い辞書は傷つかないでしょう。