🔤 🌗 ⛲️ 回転する流体の形状について 👈🏼 🌨️ 👼

今日、私はお茶を飲んで考えました

今朝、Iれたてのお茶に砂糖を2杯かき混ぜながら考えました。回転中に取る液体の形について考えました。もちろん、お茶を入れた砂糖をすばやくかき混ぜたらどうなるかは誰もが知っています。私は、このありふれたプロセスをより詳細に検討し、日常生活で私たちを取り巻く現象の物理学から興味深いことをいくつか伝えたいと思いました。

実験アイデア

液体が入っている円筒形の容器があると想像してみましょう。液体は、少なくとも2つの明白な方法で回転できます：何らかの物体で攪拌するか、円筒形容器を回転させます。これにより、液体と容器の表面との間の摩擦力により、容器を含む回転容器によって運ばれた液体が回転します。

物理モデル

2番目のオプションについて説明します。そのため、一定の周期周波数で回転する容器があり、一定の周期周波数での動的平衡の下で、液体は同じ方向に回転します。

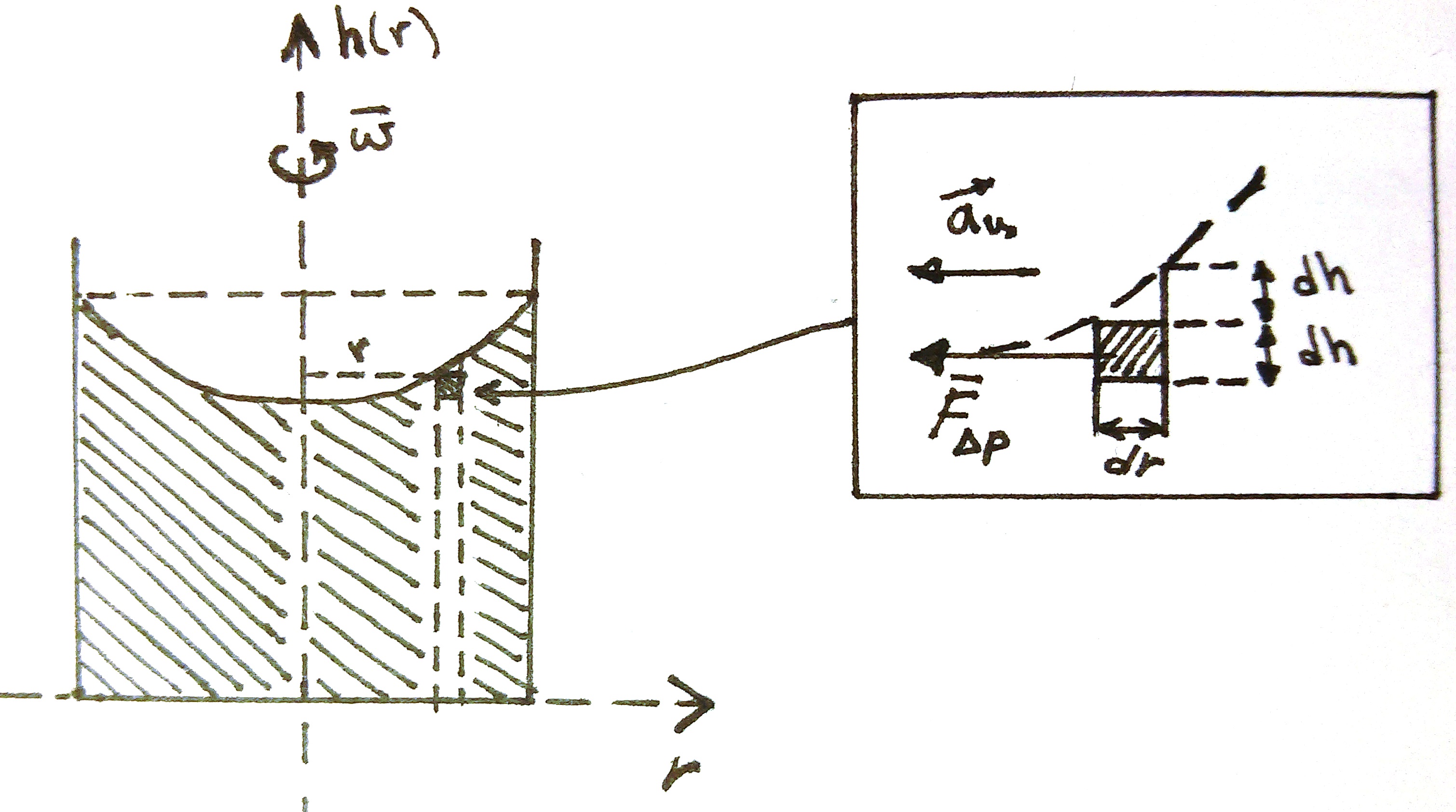
流体全体から表面近くの基本的な極小体積を切り取り、それに作用する力を検討します。問題の対称性により、円筒座標に焦点を当て、計算を大幅に簡素化します。

表面形状の定性的計算

液体の体積の基本部分に対する2番目のニュートンの法則を記述します。

m o v e r r i g h t a r r o w a = s u m l i m i t s_{i} o v e r r i g h t a r r o w F_{i}

$m \ overrightarrow a = \ sum \ limits_i {\ overrightarrow F _i}$

たとえば、brewれたてのお茶のカップに砂糖のスプーンをかき混ぜた後、液体は対称軸の周りを回転するため、ボリュームの基本部分は求心性の加速を持ちます。したがって、基本体積から対称軸への半径ベクトルと一致する軸にニュートンの法則を投影します。粘度と表面張力は考慮しません。求心加速度を与える力（運動の法則の右側）は、最初の図の拡大部分に見られる液体柱の圧力の違いにより発生します。

したがって、次の式が得られます。

ま た は ： m a_{c} = F_{D e l t a p}

$または：ma_ {c} = F _ {\ Delta p}$ どこで

a_{c} = f r a c v^{2} r = f r a c \左 （ o m e g a r \右 ）^{2} r = o m e g a^{2} r

$a_ {c} = \ frac {{v ^ 2}} {r} = \ frac {{\左（{\ omega r} \右）^ 2}} {r} = \ omega ^ 2 r$ 、そしてその同じ力は

F_{D e l t a p} = D e l t a p c d o t S_{e f f . s e c t i o n}

$F _ {\ Delta p} = \ Delta p \ cdot S_ {eff.section}$ ここで、有効断面積

S_{e f f . s e c t i o n} = r d v a r p h i c d o t d h = r d v a r p h i d h

$S_ {eff.section} = rd \ varphi \ cdot dh = rd \ varphi dh$ 液柱の圧力差が作用する基本容積の面積が示されています

D e l t a p = r h o g d h

$\ Delta p = \ rho gdh$ 。

力を得る

F_{D e l t a p} = r h o g d h c d o t r d v a r p h i d h = r h o g r d v a r p h i l e f t （ d h r i g h t ）^{2}

$F _ {\ Delta p} = \ rho gdh \ cdot rd \ varphi dh = \ rho grd \ varphi \ left（{dh} \ right）^ 2$

体積要素の質量は、すべての人になじみのある式によって決まります

m = r h o d V

$m = \ rho dV$ 、ボリューム自体は等しくなります

d V = r d v a r p h i c d o t d h c d o t d r

$dV = rd \ varphi \ cdot dh \ cdot dr$ （円筒座標の基本体積）。

その結果、私たちの小さな問題に対するニュートンの法則2は次の式で記述されます。

r h o r d v a r p h i c d o t d h c d o t d r c d o t o m e g a^{2} r = r h o g r d v a r p h i l e f t （ d h r i g h t ）^{2}

$\ rho rd \ varphi \ cdot dh \ cdot dr \ cdot \ omega ^ 2 r = \ rho grd \ varphi \ left（{dh} \ right）^ 2$

小さな削減と変換の後、以下が得られます。

\オ メ ガ^{2} r d r = g d h

$\オメガ^ 2 rdr = gdh$

ここで、不定積分を使用して式の両側を統合します。

i n t o m e g a^{2} r d r = i n t g d h

$\ int {\ omega ^ 2 rdr = \ int {gdh}}$

o m e g a^{2} f r a c r^{2} 2 = g h + c o n s t

$\ omega ^ 2 \ frac {{r ^ 2}} {2} = gh + const$

h （ r ） = f r a c o m e g a^{2} 2 g r^{2} + C

$h（r）= \ frac {{\ omega ^ 2}} {{2g}} r ^ 2 + C$

詳細な表面形状の計算

これで、表面形状の非常に明確な依存性が得られ、これが放物面であると自信を持って言えます。しかし、私たちは定数を知りません

C

$C$ 。プロセスの物理を完全に理解するために定義しましょう。

液体の量は変わらないので（お茶のツツをかき混ぜながら滴をこぼさなかったと思われます）、回転前と回転中に一定の周期周波数で体積を書き留めます。

回転前：

V = p i R^{2} H

$V = \ pi R ^ 2 H$ どこで

H

$H$ -これは、穏やかな状態（回転なし）の円筒面内の液体の高さです。

回転中：

V = i n t i n t i n t d V = i n t i n t i n t r d v a r p h i d h d r

$V = \ int {\ int {\ int {dV}}} = \ int {\ int {\ int {rd \ varphi dhdr}}}$

b e g i n a r r a y l V = i n t l i m i t s_{0}^{2 p i} d v a r p h i i n t l i m i t s_{0}^{R} r d r i n t l i m i t s_{0}^{f r a c o m e g a^{2} 2 g r^{2} + C} d h = i n t l i m i t s_{0}^{2 p i} d v a r p h i i n t l i m i t s_{0}^{R} r l e f t （ f r a c o m e g a^{2} 2 g r^{2} + C \右 ） d r = i n t l i m i t s_{0}^{2 p i} d v a r p h i i n t l i m i t s_{0}^{R} l e f t （ f r a c o m e g a^{2} 2 g r^{3} + C r r i g h t ） d r = = i n t l i m i t s_{0}^{2 p i} l e f t （ f r a c o m e g a^{2} 8 g R^{4} + f r a c C 2 R^{2} r i g h t ） d v a r p h i = l e f t （ f r a c o m e g a^{2} 8 g R^{4} + f r a c C 2 R^{2} \右 ） 2 p i = f r a c p i o m e g a^{2} 4 g R^{4} + p i C R^{2} e n d a r r a y

$\ begin {array} {l} V = \ int \ limits_0 ^ {2 \ pi} {d \ varphi} \ int \ limits_0 ^ R {rdr} \ int \ limits_0 ^ {\ frac {{\ omega ^ 2} } {{2g}} r ^ 2 + C} {dh} = \ int \ limits_0 ^ {2 \ pi} {d \ varphi} \ int \ limits_0 ^ R {r \ left（{\ frac {{\ omega ^ 2}} {{2g}} r ^ 2 + C} \右）dr} = \ int \ limits_0 ^ {2 \ pi} {d \ varphi} \ int \ limits_0 ^ R {\ left（{\ frac {{ \ omega ^ 2}} {{2g}} r ^ 3 + Cr} \ right）dr} = \\ = \ int \ limits_0 ^ {2 \ pi} {\ left（{\ frac {{\ omega ^ 2} } {{8g}} R ^ 4 + \ frac {C} {2} R ^ 2} \ right）d \ varphi} = \ left（{\ frac {{\ omega ^ 2}} {{8g}} R ^ 4 + \ frac {C} {2} R ^ 2} \右）2 \ pi = \ frac {{\ pi \ omega ^ 2}} {{4g}} R ^ 4 + \ pi CR ^ 2 \\ \ end {array}$

したがって、これらのボリュームは同等です。

p i R^{2} H = f r a c p i o m e g a^{2} 4 g R^{4} + p i C R^{2}

$\ pi R ^ 2 H = \ frac {{\ pi \ omega ^ 2}} {{4g}} R ^ 4 + \ pi CR ^ 2$

したがって、以前は未知の定数が表現されます：

C = f r a c 1 R^{2} \左 [R^{2} H - f r a c o m e g a^{2} 4 g R^{4} \右] = H - f r a c o m e g a^{2} 4 g R^{2}

$C = \ frac {1} {{R ^ 2}} \左[{R ^ 2 H-\ frac {{\ omega ^ 2}} {{4g}} R ^ 4} \右] = H-\ frac {{\ omega ^ 2}} {{4g}} R ^ 2$

そして、回転する流体の表面形状の最終方程式は次のとおりです。

h （ r ） = f r a c o m e g a^{2} 2 g r^{2} + H - f r a c o m e g a^{2} 4 g R^{2}

$h（r）= \ frac {{\ omega ^ 2}} {{2g}} r ^ 2 + H-\ frac {{\ omega ^ 2}} {{4g}} R ^ 2$ または変換

h （ r ） = f r a c o m e g a^{2} 2 g \左 （ r^{2} - f r a c R^{2} 2 \右 ） + H

$h（r）= \ frac {{\ omega ^ 2}} {{2g}} \左（{r ^ 2-\ frac {{R ^ 2}} {2}} \右）+ H$

いくつかのメモ

表面の形状は、回転数、重力加速度、容器の幾何学的パラメーター、液体の初期体積に依存するが、液体の密度には依存しないという事実に注意を喚起したいと思います。この式は、対称軸の周りを回転する円筒容器内の流体のおおよその配置を簡単にシミュレートするために使用できるため、かなり興味深いように思えました。これを行うには、MathCAD'omを使用していくつかのチャートを作成します。

計算結果のグラフィック表示

カップまたはガラスのサイズに見合った、システムの非常にリアルなパラメーターを取得します。

円筒面の半径：

R 0 ： = 0.05

$R0：= 0.05$

回転しない円筒面内の液体の高さ：

H 0 ： = 0.1

$H0：= 0.1$

自由落下加速：

g 0 ： = 9.81

$g0：= 9.81$

円筒面の周期的回転速度：

w 0

$w0$

（これらの数量のすべての値はCシステムで与えられます）

次に、MathCADで表示するように関数を書き換えます。

2Dセクション表示の場合：

h （ r ） ： = i f l e f t （ - R 0 l e r l e R 0 、 f r a c w 0^{2} 2 c d o t g 0 c d o t l e f t （ r^{2} - f r a c R 0^{2} 2 \右 ） + H 0, 0 \右 ）

$h（r）：= if \ left（{-R0 \ le r \ le R0、\ frac {{w0 ^ 2}} {{2 \ cdot g0}} \ cdot \ left（{r ^ 2-\ frac {{R0 ^ 2}} {2}} \右）+ H0,0} \右）$

3D表面ディスプレイの場合：

N 0 ： = 100

$N0：= 100$

i ： = 0.. N 0

$i：= 0..N0$

j ： = 0.. N 0

$j：= 0..N0$

x_{i} ： = 0.001 c d o t l e f t （ 2 c d o t i - N 0 r i g h t ）

$x_i：= 0.001 \ cdot \ left（{2 \ cdot i-N0} \ right）$

y_{j} ： = 0.001 c d o t l e f t （ 2 c d o t j - N 0 r i g h t ）

$y_j：= 0.001 \ cdot \ left（{2 \ cdot j-N0} \ right）$

r （ x 、 y ） ： = s q r t x^{2} + y^{2}

$r（x、y）：= \ sqrt {x ^ 2 + y ^ 2}$

h v （ x 、 y ） ： = f r a c w 0^{2} 2 c d o t g 0 c d o t l e f t （ r^{2} （ x 、 y ） - f r a c R 0^{2} 2 \右 ） + H 0

$hv（x、y）：= \ frac {{w0 ^ 2}} {{2 \ cdot g0}} \ cdot \ left（{r ^ 2（x、y）-\ frac {{R0 ^ 2}} {2}} \右）+ H0$

f h （ x 、 y ） ： = i f l e f t （ - R 0 l e r （ x 、 y ） l e R 0 、 i f （ h v （ x 、 y ） g e 0 、 h v （ x 、 y ） 、 0 ） 、 0 \右 ）

$fh（x、y）：= if \ left（{-R0 \ le r（x、y）\ le R0、if（hv（x、y）\ ge 0、hv（x、y）、0）、 0} \右）$

M_{i 、 j} ： = f h （ x_{i} 、 y_{j} ）

$M_ {i、j}：= fh（x_i、y_j）$

変更パラメータとして、周期速度を変更します

w 0

$w0$ 。結果は以下の図で見ることができます：

周期的な周波数で

w 0 = 0 （ r a d / s ）

$w0 = 0（rad / s）$

周期的な周波数で

w 0 = 5 （ r a d / s ）

$w0 = 5（rad / s）$

周期的な周波数で

w 0 = 15 （ r a d / s ）

$w0 = 15（rad / s）$

周期的な周波数で

w 0 = 25 （ r a d / s ）

$w0 = 25（rad / s）$

周期的な周波数で

w 0 = 39.5 （ r a d / s ）

$w0 = 39.5（rad / s）$

周期的な周波数で

w 0 = 90 （ r a d / s ）

$w0 = 90（rad / s）$

結論

周期的な周波数が値を超えると、

w 0 = 39.5 （ r a d / s ）

$w0 = 39.5（rad / s）$ 、その後、回転する円筒形の容器の底部が表示され、この周波数から開始して、液体が容器の壁にスムーズに「通過」し、底部がますます露出します。明らかに、非常に高い周波数では、すべての流体が血管の壁に沿って流れます。これで、このような液体のすべてのパラメーターがわかりました。その方程式がわかれば、特定の周波数で特定の高さの血管壁の液体層の厚さを計算することは難しくありません。

更新しました。それとは別に、問題を検討する際に採用された矛盾する仮定を強調したいと思います。

1.流体は、それを含む容器の回転により回転すると考えられていました。これは、内部摩擦、粘度、表面張力を考慮した場合にのみ可能です。

2.しかし、表面形状を導出する場合、これらの現象は、ソリューションを簡素化し、定性的なモデリング結果のみを表示するために考慮されません。すなわちこのソリューションは、最初に説明したモデルと矛盾しています。高周波数でのプロセスの非線形性を含むすべての現象を考慮に入れると、タスクが非常に複雑になり、分析的に解決することはほとんど不可能になり、数学/物理学に関係のない人にとっては、おおよその理解可能なモデルが示されます。

3.目標は、非常に近似した最も単純なソリューションのみを表示することであり、これには多くの仮定が含まれています。

回転する流体の形状について

今日、私はお茶を飲んで考えました

実験アイデア

物理モデル

表面形状の定性的計算

詳細な表面形状の計算

いくつかのメモ

計算結果のグラフィック表示

結論

More articles: