はじめに
技術プロセスの自動制御の最も重要なタスクは、自動制御システム（ASR）のダイナミクスの数学的記述、計算、分析の開発です。
マイクロプロセッサ制御デバイス（MCI）の工業的使用の実践は、「理想的なアルゴリズム」が物理的に実行可能でないことを示しています。 それらに基づいて合成されたASRは、実際のシステムの動作を反映していません[1]。
パルスリレーコントローラーなど、特定の条件下でのアルゴリズムの理想化されたアルゴリズムからの偏差は、アクチュエーターの速度がオブジェクトの実際のダイナミクスに対応する場合、十分な精度の実際のシステムの動作は数学モデルの結果に対応します。
パルスリレーコントローラは、次の傾向が見られるマイクロプロセッサ制御デバイスで使用されます。 たとえば、出版物[2]は、modbusプロトコルを使用して独自のPythonベースのScadaシステムを作成する可能性について説明しています。
出版物[3]は、Arduinoを操作するためのPythonの使用について説明しています。 私はこの傾向を継続し、Pythonが最終的にこの新しいアプリケーション分野を手に入れることを望んでいます。
1.Type線形制御アルゴリズム
方程式によって決定される理想的な制御アルゴリズムをもたらします。
Pアルゴリズム：
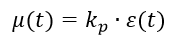
PIアルゴリズム：
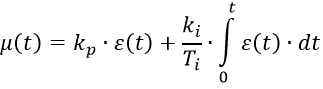
PIDアルゴリズム：
どこで
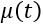-規制への影響。 
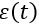-不一致信号; Kp、Ki、Kd-対応するリンクの透過係数とTi、Td時定数（コントローラー設定）。
設定を考慮に入れたレギュレーターのすべての過渡特性は、1つの一般式で表すことができ、0で割る不確実性を回避できます。
from numpy import e,arange def hp(t,Kp,Ki,Kd,Td): if t<0: z=0 elif Td==0: z=Kp+Ki*t else: z=Kp+Ki*t+Kp*Kd*e**(-t/Td) return z
理想的な形式のPIDコントローラーは物理的に実現できないため、理想をシミュレートするための形式Kp + Ki * t + Kp * Kd * e **（-t / Td）で示されることに注意してください。
理想的なレギュレーターの過渡特性
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' from numpy import e,arange def hp(t,Kp,Ki,Kd,Td): if t<0: z=0 elif Td==0: z=Kp+Ki*t else: z=Kp+Ki*t+Kp*Kd*e**(-t/Td) return z x=arange(-2,10,0.01) y=[hp(t,2,0,0,0) for t in x] y1=[hp(t,2,0.25,0,0) for t in x] y2=[hp(t,2,0.25,2,2) for t in x] plt.title(' ') plt.plot(x, y, linewidth=2, label=' ') plt.plot(x, y1, linewidth=2, label=' ') plt.plot(x, y2, linewidth=2, label=' ') plt.legend(loc='best') plt.grid(True) plt.show()
トランジェントの性質をグラフに示します：
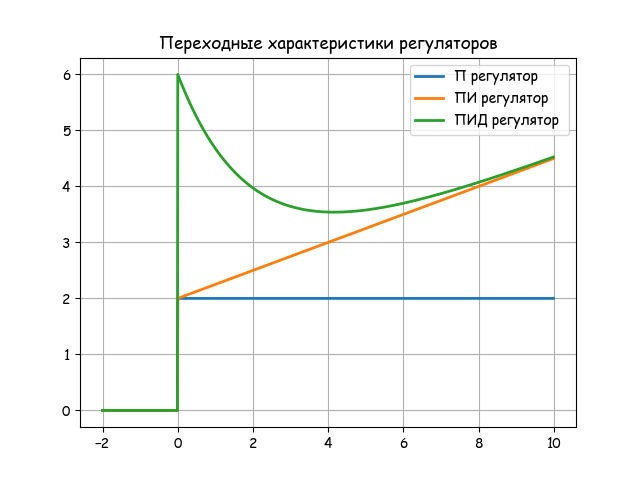
制御理論の典型的な理想的な制御アルゴリズムに基づいて、最適なパラメトリック合成の方法が開発され、ASRの一般的な特性が調査されます。
産業用自動制御装置では、一般的なアルゴリズムがほぼ実装されています。 コントローラーが「通常」モードで動作している場合、制御アルゴリズムが理想から逸脱しても、システムの動作に大きな影響はありません。
そのためには、その技術的な実装方法により、実際のアルゴリズムの本質的な特徴を知り、考慮する必要があります。 自動化の実践では、マイクロプロセッサー制御装置の仮想モジュールの形の電気（電子）間接制御装置が広く使用されています。
アルゴリズムの実装方法による自動電気コントローラーの分類を検討してください[1]：
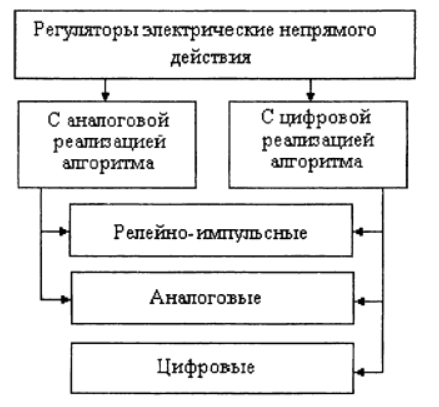
提示された分類に従って、本および以下の出版物は、Pythonを使用したレギュレーターの数学モデルの実装を検討します。
2.リレーパルスアクションのレギュレータ
自動プロセス制御システムは、一定の出力シャフト速度を備えた非同期電気可逆モーターを備えたアクチュエーター（EIM）を使用します。 これにより、規制アルゴリズムの実装方法が決まりました。
定速EIMが存在する場合のPIアルゴリズムの実装の原理は、図に示されている図で説明されています。
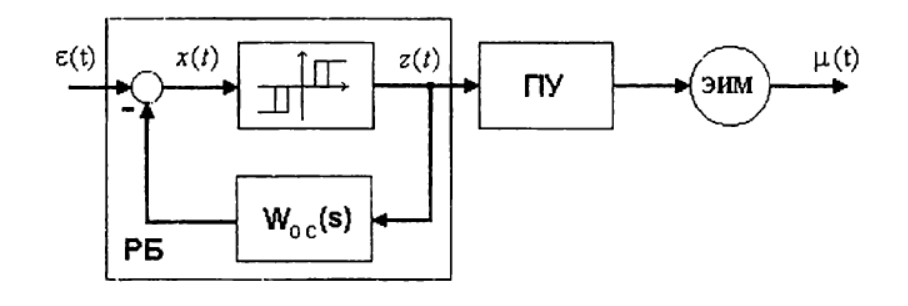
制御ユニット（RB）は、EIMを制御する一定振幅の方形波パルスを生成します。EIMの持続時間とデューティサイクルは、コントローラー設定の値と入力信号の値に依存します。
RBの直接チャネルには、非線形要素が含まれています。図に示すように、デッドゾーン∆nリターンゾーン∆vの3ポジションリレーです。
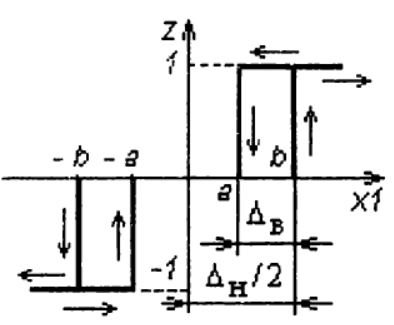
非線形要素モデル
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' from numpy import arange,sin,cos,sign def z(t,a,b): if -a<4*sin(t)<b and 4*cos(t)>0: z=0 elif -b<4*sin(t)<a and 4*cos(t)<0: z=0 else: z=sign(sin(t)) return zx=arange(0,6,0.005) y=[4*sin(t) for t in x] y1=[z(t,2,3) for t in x] y2=[2 for t in x] y3=[3 for t in x] plt.figure() plt.title(' : -') plt.plot(x, y, linewidth=2, label=' ') plt.plot(x, y1, linewidth=2, label=' ') plt.plot(x, y2, linewidth=1, label='2 ') plt.plot(x, y3,linewidth=1, label='3') plt.legend(loc='best') plt.grid(True) plt.figure() plt.title(' . ') plt.plot(y, y1, linewidth=2, label=' ') plt.legend(loc='best') plt.grid(True) plt.show()
次の2つのグラフに従って、モデルの結果を分析します。
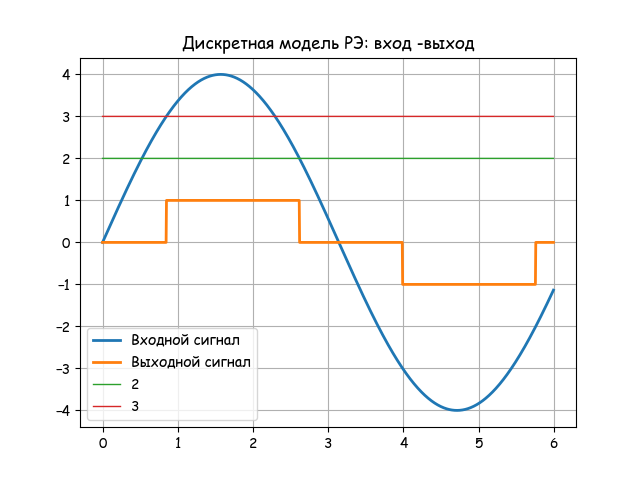
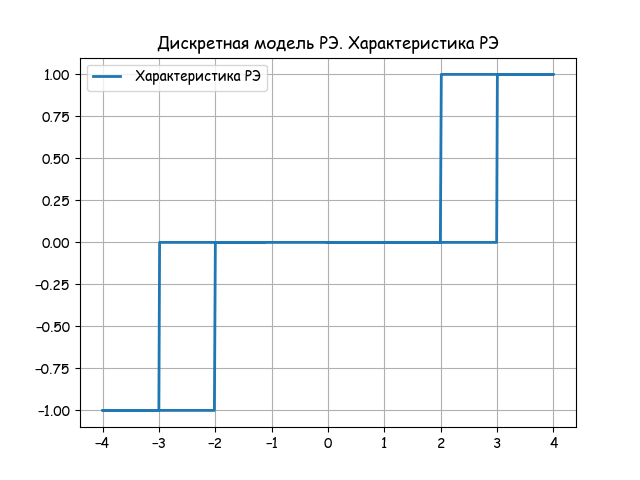
REの離散モデルは、差分方程式に基づいています。 フィードバック形成PIアルゴリズムは、伝達関数を持つ非周期的リンクを使用して実装されます。
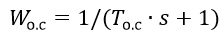
制御ユニット（RB）はパルス幅変調器（PWM）で、アナログとデジタルの両方の手段を使用して構築できます。
コントロールユニットと定速アクチュエータは、特定の条件下で、PIアルゴリズムのかなり正確な実装を提供します。
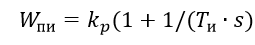（1）
それに応じて、過渡応答：
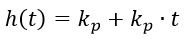（2）
PIDアルゴリズムを実装するには、微分器W（s）をスキームに従ってパルスリレーアクションのPIコントローラーの入力に接続します。
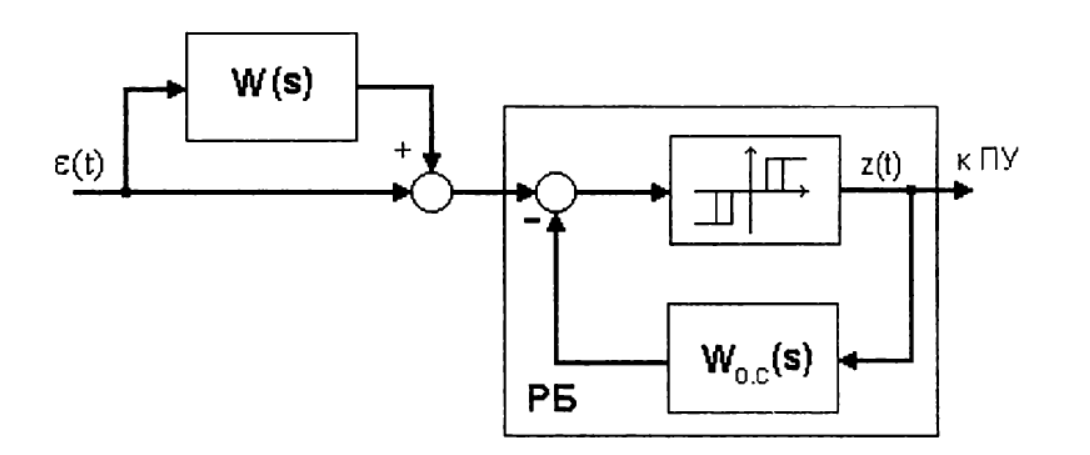
導入された伝達W（s）は、直列に接続された1つまたは2つの差別化リンクによって形成されます。 制御ユニットは、一定速度のアクチュエータとともに、特定の条件下で、PIDアルゴリズムのかなり正確な実装を提供します。
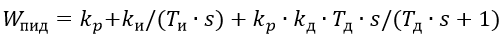（3）
それに応じて、過渡応答：
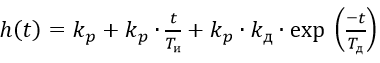（4）
PIとPIDアルゴリズムを比較するためのリスト
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' from numpy import e,arange def hp(t,Kp,Ti,Kd,Td): z=Kp+Kp*t/Ti+Kp*Kd*e**(-t/Td) return z x=arange(0,10,0.02) y1=[hp(t,2,2,0,0.5) for t in x] y2=[hp(t,2,2,4,0.5) for t in x] plt.title(' ') plt.plot(x, y1, linewidth=1, label=' ') plt.plot(x, y2, linewidth=2, label=' ') plt.legend(loc='best') plt.grid(True) plt.show()
PIおよびPIDアルゴリズムの選択された設定の過渡グラフを分析します。
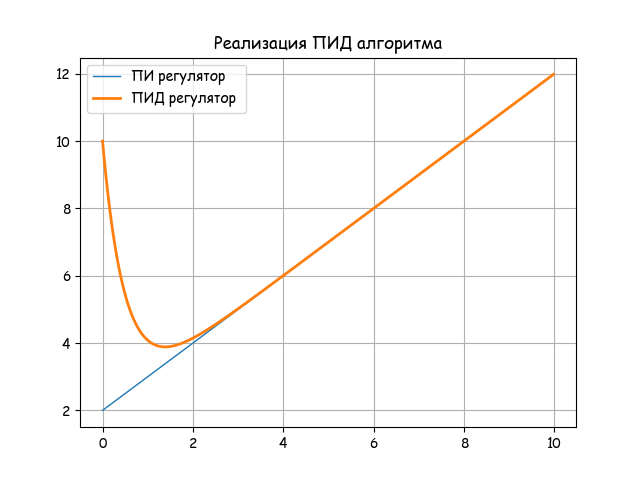
リレーパルスレギュレーターの線形モデルは、規制の影響（レギュレーターの出力値）の瞬間的な変化の可能性を排除しません。
実際のリレーパルスコントローラーでは、設定の設定値とsoアクチュエーターの速度の両方に応じて、出力シャフトまたはEIMのステムの動きが有限時間で発生します。
したがって、入力信号のステップ変化により、PアルゴリズムのRB制御ユニットの出力でのパルス幅は、比率によって決定されます。
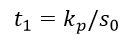
PIアルゴリズムのRBの出力での最初のパルスの持続時間は、次の方程式によって決定されます。
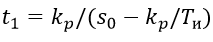
一定の持続時間tの後続のパルスは、次の時間間隔で繰り返されます。
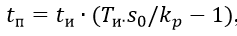
どこで
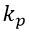-レギュレーターのギア比; 
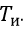-積分定数、s; 
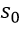-アクチュエータの速度、 
。
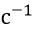3.非平衡モードでのパルスリレーP-PIおよびPIDコントローラーのダイナミクスのモデリング
パルスPIDコントローラーのグラフを次の図に示します。
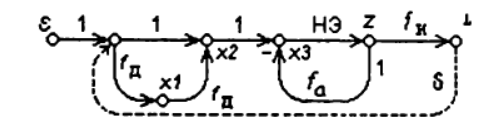
リレーパルスレギュレーターのダイナミクスのモデルのリスト
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' from numpy import arange,sign def fd(Kd,Td,dt,x,x1,y):# - () return (1-dt/Td)*y+Kd*(x-x1) def fa(Ta,Ka,dt,x,y):# ( ) return (1-dt/Ta)*y+Ka*x*dt/Ta def fi(so,dt,x,y):# ( ) return y+so*x*dt """ """ te=15;N=300;dt=0.05 x0=[0 for w in arange(0,N+1)];x1=[0 for w in arange(0,N+1)] x2=[0 for w in arange(0,N+1)];x3=[0 for w in arange(0,N+1)] z=[0 for w in arange(0,N+1)];z1=[0 for w in arange(0,N+1)] z2=[0 for w in arange(0,N+1)];m=[0 for w in arange(0,N+1)] x=[0 for w in arange(0,N+1)] """ """ def P(so,Ka,Ta,a,b,Kd,Td,Dl,e): for j in arange(0,N,1): x0[j+1]=e-Dl*m[j] x[j+1]=x0[j+1]+x2[j]-x3[j] if -a<x[j+1]<b and x[j+1]>x[j]: z1[j+1]=0 else: z1[j+1]=sign(x[j-1]) if -b<x[j+1]<a and x[j+1]<x[j]: z2[j+1]=0 else: z2[j+1]=sign(x[j-1]) if x[j+1]>x[j]: z[j+1]=z1[j+1] else: z[j+1]=z2[j+1] x1[j+1]=fd(Kd,Td,dt,x0[j+1],x0[j],x1[j]) x2[j+1]=fd(1,Ta,dt,x1[j+1],x1[j],x2[j]) x3[j+1]=fa(Ta,Ka,dt,z[j+1],x3[j]) m[j+1]=fi(so,dt,z[j],m[j]) return m NN=[j*dt for j in arange(0,N+1,1)] #P(so,Ka,Ta,a,b,Kd,Td,Dl,e) #PID=P(1,10,5,0.4,0.5,10,1,0,1) #PP=P(1,0.1,0.1,0.2,0.6,0,0.2,4,1) #PI=P(1,10,5,0.4,0.5,0,0.2,0,1) #PI1=P(0.5,10,5,0.4,0.5,0,0.2,0,1) plt.figure() plt.title(' - ') plt.plot(NN, P(1,10,5,0.4,0.5,0,0.2,0,1), linewidth=2, label=' - ') plt.plot(NN,P(1,10,5,0.4,0.5,10,1,0,1), linewidth=2, label=' - ') plt.legend(loc='best') plt.grid(True) plt.figure() plt.title(' - ') plt.plot(NN, P(1,10,5,0.4,0.5,0,0.2,0,1), linewidth=2, label=' -. -1 -1') plt.plot(NN,P(0.5,10,5,0.4,0.5,0,0.2,0,1), linewidth=2, label=' -. -0.5 -1') plt.plot(NN,P(1,0.1,0.1,0.2,0.6,0,0.2,4,1), linewidth=2, label=' -. -1 -1') plt.legend(loc='best') plt.grid(True) plt.show()
結果を分析します。
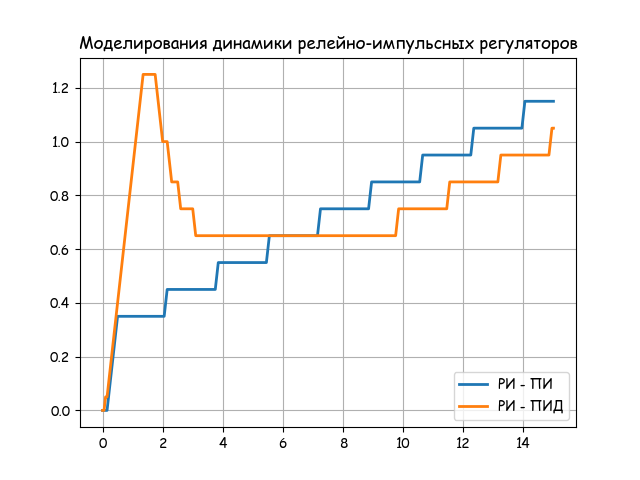
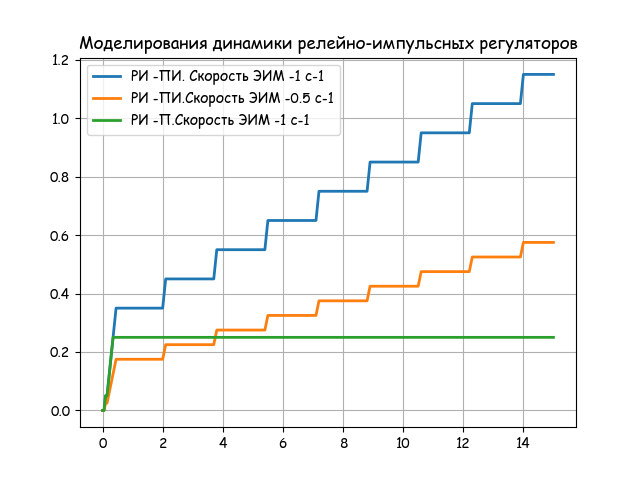
コントローラーの特性は、アクチュエーターの速度とリレー要素a、bのパラメーターの両方に依存します。 soの値はEIMのタイプによって事前に決定され、パラメーターTim（フルストロークの最小時間）によって特徴付けられます。 標準EIMの場合、Tim値は10.25.63、100、および160秒です。
b（不感帯の半分）の値は、許容偏差の値によって設定されます。これは、規制当局が応答すべきではありません。
コントローラーKr、Ti、Kd、TDの設定は、アクチュエーターの速度、フィードバックパラメーターKa、Ta、およびリレー要素a、bに非線形に依存します。
結論
Pythonプログラミング言語を使用して、差分法を使用して、間接動作の電子リレーパルスレギュレーターの数学モデルが取得されます。
結果のモデルは、マイクロプロセッサ制御デバイスの設計に使用できます。
参照資料