はじめに
制御オブジェクトの識別-観察に従ってオブジェクトの数学モデルを構築するための一連のメソッド。
この文脈における数学的モデルとは、周波数または時間領域における物体またはプロセスの振る舞いの数学的記述を意味します。例えば、物理的プロセス（外力の影響下での機械システムの動き[1]）、経済的プロセス（為替レートの変化が消費者価格に及ぼす影響商品[2]）。
現在、この制御理論の分野は実際に広く使用されているため、検討に興味深いものです。
オブジェクト自体のさまざまな性質に関連する制御オブジェクトの動的識別の分野は非常に広範囲であるため、最初は、いわゆる加速曲線の処理方法の検討に限定します。
加速曲線は、ステップ入力効果によって引き起こされる時変出力変数のプロセスを指します。 加速曲線は、オブジェクトの動的プロパティを決定するために使用されます。
問題の声明
1.正規化された過渡応答（加速曲線）に従って制御オブジェクトの動的識別の数学モデルを構築するには：
•導関数を使用した最小二乗法。
•修正面積法。
2.取得した数学的モデルの妥当性を決定し、制御オブジェクトと比較します。
理論
識別は、オブジェクトに適切なモデルを見つけることにあります。 構造とパラメーターの識別を区別します。 構造同定では、モデルの形状は特定のクラスの関数から決定され、パラメトリック同定では、モデルのパラメーターが決定されます。
オブジェクトY（t）の出力信号が、観測された入力効果X（t）によって完全に決定される場合、アクティブな実験の方法を使用してそれを特定すれば十分です。
初期情報は、実験的に記録された加速度曲線です。時間間隔0≤t≤Tにおける入力Y（t）に対するオブジェクトY（t）の応答です。
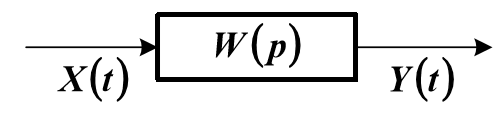
これは、演算子伝達関数W（p）を持つオブジェクトモデルの構造図です。 オブジェクトの動的特性の方程式は、次の形式で任意に表すことができます。
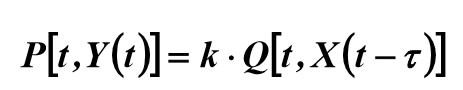
（1）
どこで
-オブジェクトの遅延時間。信号がオブジェクトの入力に入力された瞬間から信号がその出力に現れるまでの時間。 kはオブジェクトのゲイン（または透過係数）です。
オブジェクトの遅延時間とゲインを決定するためのスキーム：
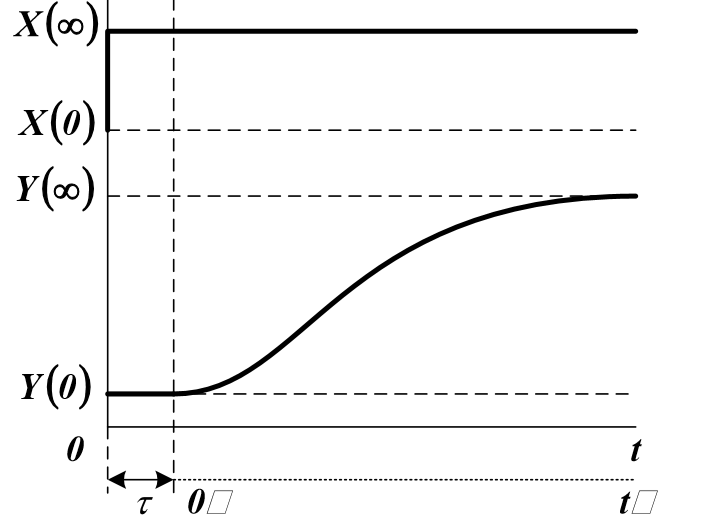
入力値と出力値は、通常、0から1（正規化）の標準範囲でスケーリングされます。
kを決定した後
時間スケールを右に動かすことにより、オブジェクトを正規化された座標で遅滞なく探索できます。 [3]。
構造物の識別
構造の識別では、オブジェクトのアプリオリ情報を使用してモデルの構造を決定します。
ダイナミクス方程式は通常、線形または線形化された特性のクラスから選択されます。 正規化された座標では、集中パラメータ、1つの入力、1つの出力信号を持つオブジェクトモデルは、定数係数を持つ常微分方程式です。
（2）
係数はどこですか
そして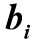 
対応する項の導関数の次数に等しい次数の時間の次元を持ちます。 物理的に実行可能なシステムでは、n≥m
加速曲線の形式により、たとえば1次オブジェクトの場合、将来のモデルの次数をおおよそ決定できます。
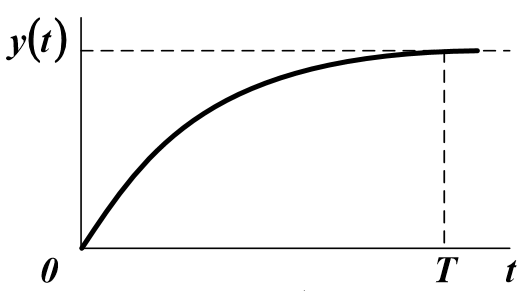
高次のオブジェクトの場合：
通常、X（t）はステップ関数であるため、式（1）の次数はオブジェクトの加速度曲線の形状によってほぼ決定できます。 この特性に変曲点がない場合、n = 1です。t=tで変曲がある場合、t/ T <0.1 ... 0.15、n =2。それ以外の場合、n> 2を考慮します。ただし、架空の遅延を導入することにより、モデルの次数を減らすことができます。
おわりに
X（t）とY（t）の測定誤差と情報処理の数値的手法の誤差の影響により、通常、3次または4次よりも高いモデルの使用は不適切になります。
パラメトリックオブジェクトの識別
パラメトリック識別では、オブジェクトに関するデータが処理されて、オブジェクトに関する事後情報が取得されます。 この場合、選択したモデルのパラメーターが評価されます。 最も単純なケースでは、このような評価は過渡応答グラフに従って実行できます。
微分を使用した最小二乗パラメトリック識別
任意の次数のオブジェクトを識別するには、最小二乗法を使用します。これには、式（2）の右辺と左辺の残差の平均二乗を最小化する必要があります。
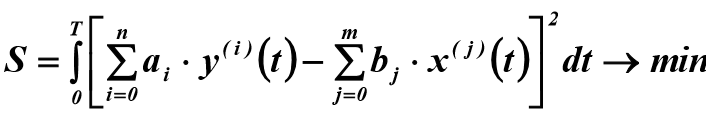（3）
ここで：
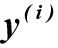そして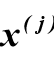 
-出力および入力信号の関数のi次およびj次の導関数。
問題の解決策（3）は、システムの解決策に還元されます。
（4）
式（3）に従って（4）を変換すると、線形代数方程式のシステムを取得できます。
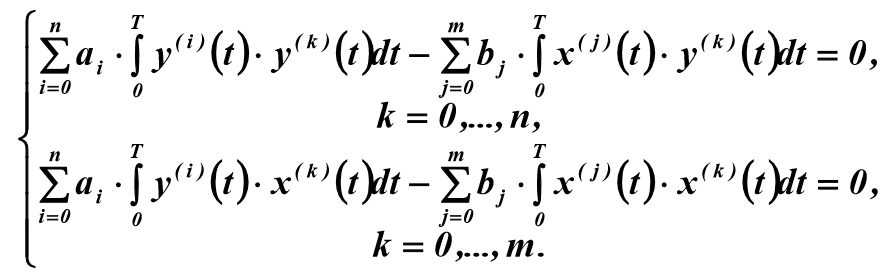（5）
未知のパラメーターに関してシステム（5）を解くには
オブジェクトの入力信号と出力信号の導関数を知る必要があります。これは、セグメントの関数X（t）とY（t）を平滑化した結果です。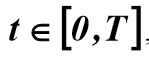 
。 係数を計算するには 
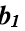数式が使用されます：
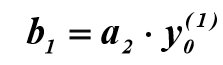
おわりに
原則として、数値微分の誤差は非常に高いため、係数を決定するためのスキーム
X（t）とY（t）の分析式の区別を使用する必要があります。
変更された面積のパラメトリック識別
Pythonを使用してモデルを作成するには、面積法の修正は一定の時間スケールで構成されます。 古典的なバージョンでは、新しい時間スケールが導入され、数値的に解くと、追加のエラーが発生します。
通常、伝達関数の式は、次の3つの数学モデルのいずれかの形式で求められます。
モデルの伝達関数の逆数である式1 / W（p）は、p次の級数で展開できます。
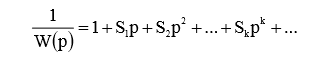
簡約伝達関数の係数a、bは、次の方程式系により係数Sに関連付けられます。
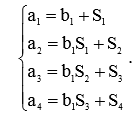
係数Siは、関係によって遷移関数h（t）に関連しています。
（6）
おわりに
関係（6）は、h（t）を3次スプラインで補間することによりPythonで解くのに最適です。これは例で証明されます。
制御オブジェクトを識別するための数学的モデルの妥当性の評価
最適なモデルを選択するには、2次の適切なインデックスを使用するだけで十分です。
（7）
どこで
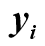-加速曲線から取得したデータ、 
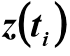-モデルの伝達関数の実部Re（W（i×w））から計算された値（周波数領域から一時領域への遷移）：
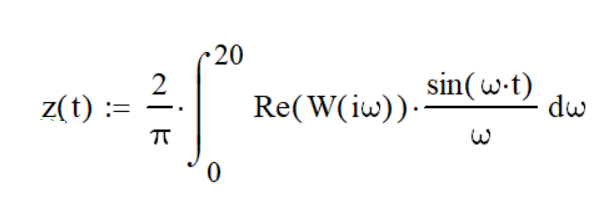（8）
最高は、最大値を提供するモデルと見なされるべきです
方程式系（5）を解く際の数値微分の大きな誤差を考えると、記号微分を実現します。 これを行うには、次のリストに従って多項式補間を適用します。
# -*- coding: utf8 -*- import matplotlib.pyplot as plt# import time start = time.time() import scipy as sp# import numpy as np# from sympy import *# import scipy.integrate as spint from scipy.integrate import quad x=[0.0, 0.4, 0.8, 1.2, 1.6 ,2.0, 2.4, 2.8 ,3.2, 3.6]# y=[0.00, 0.11, 0.36, 0.61, 0.79, 0.89, 0.94, 0.98, 0.99, 1.00]# fp, residuals, rank, sv, rcond = sp.polyfit(x, y,4, full=True)# a=round(fp[0],4);b=round(fp[1],4);c=round(fp[2],4) d=round(fp[3],4);e=round(fp[4],4) t=symbols('t ' ,real=True) def h(t):# h(t) return a*t**4+b*t**3+c*t**2+d*t+e ''' ''' L1=integrate(h(t).diff(t)*h(t).diff(t,t),(t,0,3.6)) L2=integrate(h(t).diff(t,t)*h(t).diff(t,t),(t,0,3.6)) L3=integrate(h(t).diff(t)*h(t).diff(t),(t,0,3.6)) L4=integrate((1-h(t))*h(t).diff(t,t),(t,0,3.6)) L5=integrate((1-h(t))*h(t).diff(t),(t,0,3.6)) """ (5) (3)""" P= np.zeros([2,2]) P[0,0]=L2;P[0,1]=L1 P[1,0]=L1;P[1,1]=L3 Q= np.zeros([2,1]) Q[0,0]=L4;Q[1,0]=L5 P=np.matrix(P); Q=np.matrix(Q) C=PI*Q ''' ''' a2=C[0,0] a1=C[1,0] b1=C[0,0]*h(t).diff(t).subs(t,0) a2=round(C[0,0],3) a1=round(C[1,0],3) b1=round(C[0,0]*h(t).diff(t).subs(t,0),3) """ (8)""" def ff(x,t): j=(-1)**0.5 return (2/np.pi)*( ((b1*x*j+1)/(a2*(x*j)**2+a1*x*j+1)).real)*(np.sin(x*t)/x) z=np.array([round(quad(lambda x: ff(x,t),0, 20)[0],2) for t in x]) """ (7) """ k=round(1-sum([(y[i]-z[i])**2 for i in np.arange(0,len(y)-1,1)])/sum([(y[i])**2 for i in np.arange(0,len(y)-1,1)]),5) stop = time.time() print (" :",round(stop-start,3)) plt.title(' \n -%s'%k) plt.plot(x, y,'o', label=' ') plt.plot(x, z,'r', label=' W=(%s*p+1)/(%s*p**2+%s*p+1)'%(b1,a2,a1)) plt.legend(loc='best') plt.grid(True) plt.show()
取得するもの：
プログラム実行時間：0.802
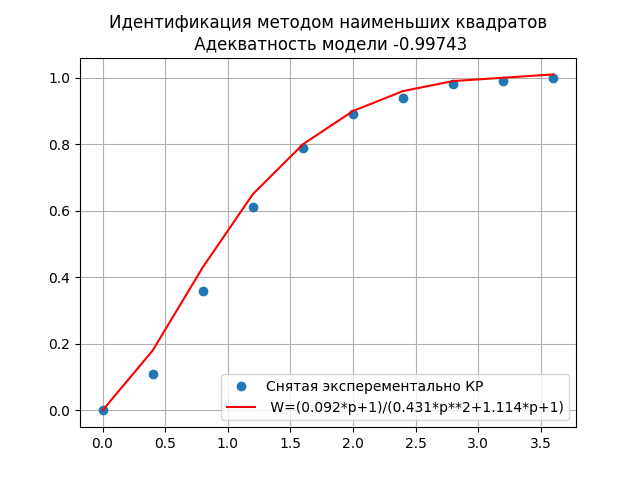
モデル0.99743の高度な妥当性は、結果の伝達関数が次のことを示しています。
W =（0.092 * p + 1）/（0.431 * p ** 2 + 1.114 * p + 1） 、
オブジェクトの動的プロパティを正確に反映します。
加速曲線は実験的に得られたものです。したがって、安定性[4]とレギュレーターのパラメーターの決定[5]についてのオブジェクトの制御システムのさらなる調査が実用的な重要性を獲得しています。
モディファイドエリアメソッドを使用してオブジェクトを識別するタスクのPythonツールによる実装
この問題を解決するには、モデルに微分が含まれていないため、数値法を使用できます。また、関係式（6）に従って提案される解法は、時間座標の変化を意味しません。 さらに、次のリストに従ってスプライン補間を適用します。
# -*- coding: utf8 -*- import matplotlib.pyplot as plt import time start = time.time() from scipy.interpolate import splev, splrep import scipy.integrate as spint import numpy as np from scipy.integrate import quad xx =np.array([0.0, 0.4, 0.8, 1.2, 1.6 ,2.0, 2.4, 2.8 ,3.2, 3.6]) yy =np.array([0.00, 0.11, 0.36, 0.61, 0.79, 0.89, 0.94, 0.98, 0.99, 1.00]) """ """ def h(x): spl = splrep(xx , yy ) return splev(x, spl) """ (6)""" S1=(spint.quad(lambda x:1-h(x),xx[0],xx[len(xx)-1])[0]) S2=(spint.quad(lambda x:(1-h(x))*(S1-x),xx[0],xx[len(xx)-1])[0]) S3=(spint.quad(lambda x:(1-h(x))*(S2-S1*x+(1/2)*x**2),xx[0],xx[len(xx)-1])[0]) S4=(spint.quad(lambda x:(1-h(x))*(S3-S2*x+S1*(1/2)*x**2-(1/6)*x**3),xx[0],xx[len(xx)-1])[0]) """ """ b1=-S4/S3 a1=b1+S1 a2=b1*S1+S2 a3=b1*S2+S3 """ """ def ff(x,t): j=(-1)**0.5 return (2/np.pi)*( ((b1*x*j+1)/(a3*(x*j)**3+a2*(x*j)**2+a1*x*j+1)).real)*(np.sin(x*t)/x) y=np.array([round(quad(lambda x: ff(x,t),0, 20)[0],2) for t in xx]) """ """ k=round(1-sum([(yy[i]-y[i])**2 for i in np.arange(0,len(yy)-1,1)])/sum([(yy[i])**2 for i in np.arange(0,len(yy)-1,1)]),5) stop = time.time() print (" :",round(stop-start,3)) plt.title(' .\n -%s'%k) plt.plot(xx, yy,'o', label=' ()') plt.plot(xx, y,'r', label='W=(%s*p+1)/(%s*p**3+%s*p**2+%s*p+1)'%(round(b1,3),round(a3,3),round(a2,3),round(a1,3))) plt.legend(loc='best') plt.grid(True) plt.show()
取得するもの：
プログラム実行時間：0.238
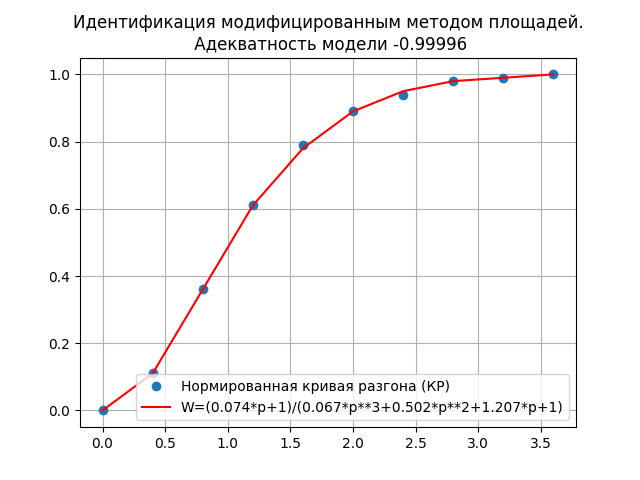
モデル0.99996の高度な妥当性と、シンボリックな微分よりも高速であるということは、伝達関数が次のことを示唆しています。
W =（0.074 * p + 1）/（0.067 * p ** 3 + 0.502 * p ** 2 + 1.207 * p + 1）） 、
近代化された面積法によって得られたものは、オブジェクトの動的特性をよりよく反映しています。
結論
1.この出版物は、制御オブジェクトの動的識別の基本を紹介しています。
2.多項式およびスプラインによる遷移関数の明示的表現の使用例とともに、自由に配布されるPythonプログラミング言語での識別問題の解決策の実装は、Pythonの範囲を拡大するのに役立ちます。
3.同定問題の数値解法については、時間座標を変更せずに結果を得ることができる関係（6）の使用を提案できます。