Pythonのたたみ込みネットワーク。 パート2.モデルトレーニングの式の導出

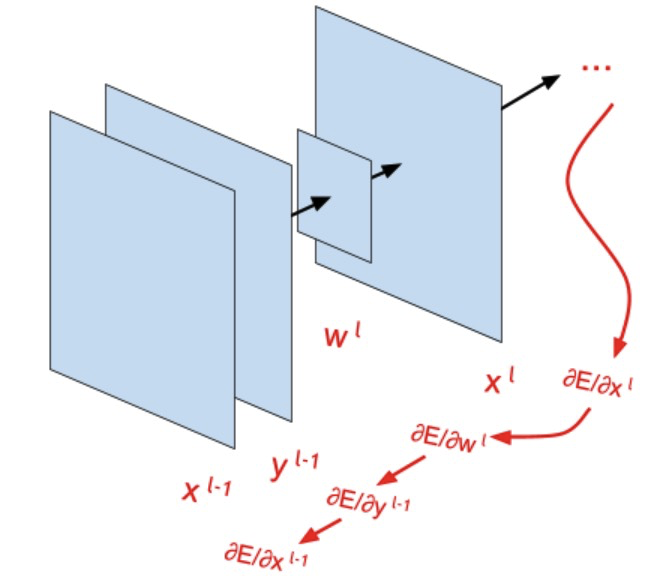
前回の記事では、将来のモデルを構成するすべてのレイヤーと機能を概念的に検討しました。 今日は、このモデルのトレーニングを担当する公式を導き出します。 損失関数から始めて畳み込み層で終わる、逆順で層を解析します。 数式を理解するのが困難な場合は、エラーの逆伝播法の詳細な説明 （写真）を理解し、 複雑な関数の微分規則を覚えておくことをお勧めします。

損失関数を介したエラーの逆伝播の公式の導出

これは、損失関数の偏微分です。 $$$E$ モデル出力。

$$

$$\ begin {array} {rcl} \ dfrac {\ partial E} {\ partial y ^ {l} _ {i}}＆=＆\ dfrac {\ partial \ frac {1} {2} \ sum_ {i = 0} ^ {n}（y ^ {truth} _i-y ^ l_i）^ 2} {\ partial y ^ {l} _ {i}} \\＆=＆\ dfrac {\ partial \ frac {1} { 2}（（y ^ {truth} _0-y ^ l_0）^ 2 + \ ldots +（y ^ {truth} _i-y ^ l_i）^ 2 + \ ldots +（y ^ {truth} _n-y ^ l_n）^ 2）} {\ partial y ^ {l} _ {i}} \\＆=＆\ dfrac {\ partial \ frac {1} {2}（y ^ {truth} _i-y ^ l_i）^ 2} { \パーシャルy ^ {l} _ {i}} = \ frac {1} {2} \ cdot2 \ cdot（y ^ {truth} _i-y ^ l_i）^ {2-1} \ cdot \ frac {\ partial （y ^ {truth} _i-y ^ l_i）} {\ partial y ^ {l} _ {i}} \\＆=＆（y ^ {truth} _i-y ^ l_i）\ cdot（-1）= y ^ l_i-y ^ {真理} _i \ end {array}$$

デリバティブ $$$\ partial \ frac {1} {2}（y ^ {真実} _i-y ^ l_i）^ 2$ 分子では、複素関数の導関数として扱います。 $$$（u ^ n） '= nu ^ {n-1} \ cdot u'$ 。 ここで、ところで、人はどのように見ることができます $$$\ frac {1} {2}$ そして $$$2$ 、そして最初に式に追加した理由が明らかになります $$$\ frac {1} {2}$



最初は標準偏差を使用しましたが、分類問題にはクロスエントロピーを使用する方が適切です（説明付きのリンク ）。 以下は、backpropの式です。可能な限り詳細な式の出力を記述しようとしました。

$$

$$\ begin {array} {rcl} \ dfrac {\ partial E} {\ partial y ^ {l} _ {i}}＆=＆\ dfrac {\ partial（-\ sum_ {i = 0} ^ {n} （y ^ {truth} _i \ cdot ln（y ^ l_i））} {\ partial y ^ {l} _ {i}} \\＆=＆\ dfrac {\ partial（-（y ^ {truth} _0 ln （y ^ l_0）+ \ ldots + y ^ {truth} _i ln（y ^ l_i）+ \ ldots + y ^ {truth} _n ln（y ^ l_n））} {\ partial y ^ {l} _ {i }} \\＆=＆\ dfrac {\ partial（-y ^ {truth} _i ln（y ^ l_i））} {\ partial y ^ {l} _ {i}} =-\ dfrac {y ^ {truth } _i} {y ^ l_i} \ end {array}$$

覚えておいて $$$\ large ln（x） '= \ frac {1} {x}$

アクティベーション関数を介したbackprop式の導出

... ReLU経由

$$

$$f '_ {ReLU} = \ frac {\ mathrm {\ partial} y ^ l_i} {\ mathrm {\ partial} x ^ l_i} = \ left \ {\ begin {matrix} 1、＆if \ enspace x ^ l_i> 0 \\ 0、その他の場合\\ \ end {matrix} \ right。$$

どこで $$$\ large \ frac {\ partial y ^ {l} _i} {\ partial x ^ l_i}$ -アクティベーション機能によるバックプロップの指定。



つまり、アクティベーション関数を直接通過する際に最大で選択された要素にエラーを渡し（前のレイヤーからのエラーを1倍します）、選択されなかったため結果に影響を与えなかった要素にはパスしません（乗算します）前のレイヤーからゼロへのエラー）。

... シグモイドを通して

$$

$$\ begin {array} {rcl} f '_ {sigmoid}＆=＆\ dfrac {\ mathrm {\ partial}} {\ mathrm {\ partial} x ^ l_i} \ left（\ dfrac {1} {1+ e ^ {-x ^ l_i}} \ right）= \ dfrac {\ mathrm {\ partial}} {\ mathrm {\ partial} x ^ l_i}（1 + e ^ {-x ^ l_i}）^ {-1 } \\＆=＆-（1 + e ^ {-x ^ l_i}）^ {-2}（-e ^ {-x ^ l_i}）= \ dfrac {e ^ {-x ^ l_i}} {（ 1 + e ^ {-x ^ l_i}）^ 2} \\＆=＆\ dfrac {1} {1 + e ^ {-x ^ l_i}} \ cdot \ dfrac {e ^ {-x ^ l_i}} {1 + e ^ {-x ^ l_i}} = \ dfrac {1} {1 + e ^ {-x ^ l_i}} \ cdot \ dfrac {（1 + e ^ {-x ^ l_i}）-1} {1 + e ^ {-x ^ l_i}} \\＆=＆\ dfrac {1} {1 + e ^ {-x ^ l_i}} \ cdot \ left（\ dfrac {1 + e ^ {-x ^ l_i}} {1 + e ^ {-x ^ l_i}}-\ dfrac {1} {1 + e ^ {-x ^ l_i}} \右）= \ dfrac {1} {1 + e ^ {-x ^ l_i}} \ cdot \ left（1- \ dfrac {1} {1 + e ^ {-x ^ l_i}} \ right）\\＆=＆f_ {sigmoid} \ cdot（1-f_ {sigmoid}）\終了{配列}$$

ここで覚えておく必要があります $$$（e ^ {u（x）}） '= e ^ {u（x）} \ cdot（u（x））'$

同時に $$$\ large f_ {sigmoid} = \ frac {1} {1 + e ^ {-x ^ l_i}}$ シグモイド式です



さらに示す $$$\ large \ frac {\ partial E} {\ partial x ^ l_i}$ どうやって $$$\大\デルタ^ l_i$ （どこ $$$\ large \ frac {\ partial E} {\ partial x ^ l_i} = \ frac {\ partial E} {\ partial y ^ l_i} \ frac {\ partial y ^ l_i} {\ partial x ^ l_i}$ ）

...また、softmax経由 （またはこちら ）

i番目の出力のsoftmax関数はその計算だけに依存しないため、これらの計算はもう少し複雑に思えました。 $$$x ^ l_i$ 他のすべてからも $$$x ^ l_j \エンスペース\ forall i、j \ in（0、...、n）$ 、その合計は、ネットワークを直接通過する公式の分母にあります。 したがって、backpropの式は2つに「分割」されます。 $$$x ^ l_i$ そして $$$x ^ l_j$ ：

$$

$$\ begin {array} {rcl} \ dfrac {\ partial y ^ l_i} {\ partial x ^ l_i}＆=＆\ dfrac {\ partial} {\ partial x ^ l_i} \ left（\ dfrac {e ^ { x ^ l_i}} {\ sum_ {k = 0} ^ {n} e ^ {x ^ l_k}} \右）= \ dfrac {e ^ {x ^ l_i} \ cdot \ sum_ {k = 0} ^ { n} e ^ {x ^ l_k}-e ^ {x ^ l_i} \ cdot e ^ {x ^ l_i}} {\ left（\ sum_ {k = 0} ^ {n} e ^ {x ^ l_k} \右）^ 2} \\＆=＆\ dfrac {e ^ {x ^ l_i} \ cdot \ left（\ sum_ {k = 0} ^ {n} e ^ {x ^ l_k}-e ^ {x ^ l_i } \右）} {\ sum_ {k = 0} ^ {n} e ^ {x ^ l_k} \ cdot \ sum_ {k = 0} ^ {n} e ^ {x ^ l_k}} = y ^ l_i \ cdot \ dfrac {\ sum_ {k = 0} ^ {n} e ^ {x ^ l_k}-e ^ {x ^ l_i}} {\ sum_ {k = 0} ^ {n} e ^ {x ^ l_k} } \\＆=＆y ^ l_i \ cdot \ left（\ dfrac {\ sum_ {k = 0} ^ {n} e ^ {x ^ l_k}} {\ sum_ {k = 0} ^ {n} e ^ { x ^ l_k}}-\ dfrac {e ^ {x ^ l_i}} {\ sum_ {k = 0} ^ {n} e ^ {x ^ l_k}} \右）= y ^ l_i \ cdot（1-y ^ l_i）\ end {array}$$

式を適用します $$$\大\左（\ frac {u} {v} \右） '= \ frac {u'v-uv'} {v ^ 2}$ どこで $$$u = e ^ {x ^ l_i}$ そして $$$\ large v = \ sum_ {k = 0} ^ {n} e ^ {x ^ l_k}$

同時に $$$\ large \ frac {\ partial} {\ partial x ^ l_i} \ sum_ {k = 0} ^ {n} e ^ {x ^ l_k} = \ frac {\ partial（e ^ {x ^ l_0} + \ ldots + e ^ {x ^ l_i} + \ ldots + e ^ {x ^ l_n}）} {\ partial x ^ l_i} = \ frac {\ partial e ^ {x ^ l_i}} {\ partial x ^ l_i} = e ^ {x ^ l_i}$



そして、の偏微分 $$$x ^ l_j$ ：

$$

$$\ begin {array} {rcl} \ dfrac {\ partial y ^ l_i} {\ partial x ^ l_j}＆=＆\ dfrac {\ partial} {\ partial x ^ l_j} \ left（\ dfrac {e ^ { x ^ l_i}} {\ sum_ {k = 0} ^ {n} e ^ {x ^ l_k}} \右）= \ dfrac {0 \ cdot \ sum_ {k = 0} ^ {n} e ^ {x ^ l_k}-e ^ {x ^ l_i} \ cdot e ^ {x ^ l_j}} {\ left（\ sum_ {k = 0} ^ {n} e ^ {x ^ l_k} \ right）^ 2} \ \＆=＆\ dfrac {e ^ {x ^ l_i} \ cdot e ^ {x ^ l_j}} {\ sum_ {k = 0} ^ {n} e ^ {x ^ l_k} \ cdot \ sum_ {k = 0} ^ {n} e ^ {x ^ l_k}} =-y ^ l_i \ cdot y ^ l_j \ end {array}$$

上記の式に基づいて、エラーが逆方向に伝播するときに関数が（コードで）返す必要のあるニュアンスがあります $$$\ large \ frac {y ^ l} {x ^ l}$ この場合、1つを計算するため、softmaxで $$$y_i ^ l$ すべて使用されています $$$x ^ l$ または、言い換えれば、それぞれ $$$x_i ^ l$ すべてに影響する $$$y ^ l$ ：







ソフトマックスの場合 $$$\ large \ frac {\ partial E} {\ partial x ^ l_i}$ 等しくなります $$$\ large \ sum_ {k = 0} ^ {n} \ frac {\ partial E} {\ partial y ^ l_k} \ frac {\ partial y ^ l_k} {\ partial x ^ l_i}$ （金額が登場しました！）、つまり：

$$

$$\ frac {\ partial E} {\ partial x ^ l_i} = \ frac {\ partial E} {\ partial y ^ l_0} \ frac {\ partial y ^ l_0} {\ partial x ^ l_i} + ... + \ frac {\ partial E} {\ partial y ^ l_1} \ frac {\ partial y ^ l_1} {\ partial x ^ l_i} + ... + \ frac {\ partial E} {\ partial y ^ l_n} \ frac {\ partial y ^ l_n} {\ partial x ^ l_i} \ qquad \ forall i \ in（0、... n）$$

この場合、値 $$$\ large \ frac {\ partial E} {\ partial y ^ l_k}$ すべてのために $$$k$ 損失関数を介してこのバックプロップがあります。 見つけることが残っている $$$\ large \ frac {\ partial y ^ l_k} {\ partial x ^ l_i}$ すべてのために $$$k$ そしてすべて $$$i$ -つまり、マトリックスです。 展開された形式の行列乗算の下 $$$\ large \ frac {\ partial y ^ l_k} {\ partial x ^ l_i}$ -行列と行列の乗算はどこから来ますか。

$$

$$\ begin {bmatrix}＆\ frac {\ partial E} {\ partial x ^ {l} _ {0}}＆\ frac {\ partial E} {\ partial x ^ {l} _ {1}}＆。 ..＆\ frac {\ partial E} {\ partial x ^ {l} _ {n}} \ end {bmatrix} = \\ = \ scriptsize \ begin {bmatrix}＆（\ frac {\ partial E} {\部分y ^ {l} _ {0}} \ frac {\ partial y ^ {l} _ {0}} {\ partial x ^ {l} _ {0}} + \ frac {\ partial E} {\ partial y ^ {l} _ {1}} \ frac {\ partial y ^ {l} _ {1}} {\ partial x ^ {l} _ {0}} + \ ldots + \ frac {\ partial E} {\部分y ^ {l} _ {n}} \ frac {\ partial y ^ {l} _ {n}} {\ partial x ^ {l} _ {0}}）＆（\ frac {\ partial E} { \ partial y ^ {l} _ {0}} \ frac {\ partial y ^ {l} _ {0}} {\ partial x ^ {l} _ {1}} + \ frac {\ partial E} {\部分y ^ {l} _ {1}} \ frac {\ partial y ^ {l} _ {1}} {\ partial x ^ {l} _ {1}} + \ ldots + \ frac {\ partial E} { \ partial y ^ {l} _ {n}} \ frac {\ partial y ^ {l} _ {n}} {\ partial x ^ {l} _ {1}}）＆...＆（\ frac { \部分E} {\部分y ^ {l} _ {0}} \ frac {\部分y ^ {l} _ {0}} {\部分x ^ {l} _ {n}} + \ frac {\部分E} {\部分y ^ {l} _ {1}} \ frac {\部分y ^ {l} _ {1}} {\部分x ^ {l} _ {n}} + \ ldots + \ frac { \部分E} {\部分y ^ {l} _ {n}} \ frac {\部分y ^ {l} _ {n}} {\部分x ^ {l} _ {n}}）\ end {bmatrix } \\ = \ begin { bmatrix}＆\ frac {\ partial E} {\ partial y ^ {l} _ {0}}＆\ frac {\ partial E} {\ partial y ^ {l} _ {1}}＆...＆\ frac {\ partial E} {\ partial y ^ {l} _ {n}} \ end {bmatrix} \ begin {bmatrix}＆\ frac {\ partial y ^ {l} _ {0}} {\ partial x ^ {l} _ {0}}＆\ frac {\ partial y ^ {l} _ {0}} {\ partial x ^ {l} _ {1}}＆...＆\ frac {\ partial y ^ { l} _ {0}} {\ partial x ^ {l} _ {n}} \\＆\ frac {\ partial y ^ {l} _ {1}} {\ partial x ^ {l} _ {0} }＆\ frac {\ partial y ^ {l} _ {1}} {\ partial x ^ {l} _ {1}}＆...＆\ frac {\ partial y ^ {l} _ {1}} {\ partial x ^ {l} _ {n}} \\＆...＆...＆...＆... \\＆\ frac {\ partial y ^ {l} _ {n}} { \ partial x ^ {l} _ {0}}＆\ frac {\ partial y ^ {l} _ {n}} {\ partial x ^ {l} _ {1}}＆...＆\ frac {\部分的なy ^ {l} _ {n}} {\部分的なx ^ {l} _ {n}} \\ \ end {bmatrix}$$

それは分解のこの最後の行列についてでした- $$$\ large \ frac {\ partial y ^ l} {\ partial x ^ l}$ 。 行列を乗算する方法をご覧ください $$$\ large \ frac {\ partial E} {\ partial y ^ l}$ そして $$$\ large \ frac {\ partial y ^ l} {\ partial x ^ l}$ 私たちは得る $$$\ large \ frac {\ partial E} {\ partial x ^ l}$ 。 したがって、softmaxのbackprop関数（コード内）の出力は行列でなければなりません $$$\ large \ frac {\ partial y ^ l} {\ partial x ^ l}$ 、その時点で既に計算されているものを掛けたとき $$$\ large \ frac {\ partial E} {\ partial y ^ l}$ 取得します $$$\ large \ frac {\ partial E} {\ partial x ^ l}$ 。

完全に接続されたネットワークを介したバックプロップ

重み行列を更新するためのbackprop式の出力 $$$w ^ l$ fcネットワーク

$$

$$\ begin {array} {rcl} \ dfrac {\ partial E} {\ partial w ^ l_ {ki}}＆=＆\ dfrac {\ partial E} {\ partial y ^ l_i} \ dfrac {\ partial y ^ l_i} {\ partial x ^ l_i} \ dfrac {\ partial x ^ l_i} {\ partial w ^ l_ {ki}} = \ delta ^ l_i \ cdot \ dfrac {\ partial x ^ l_i} {\ partial w ^ l_ {ki}} = \ delta ^ l_i \ cdot \ dfrac {\ partial \ left（\ sum ^ m_ {k '= 0} w ^ l_ {k'i} y ^ {l-1} _ {k'} + b ^ l_i \ right）} {\ partial w ^ l_ {ki}} \\＆=＆\ delta ^ l_i \ cdot \ dfrac {\ partial \ left（w ^ l_ {0i} y ^ {l-1} _ {0} + \ ldots + w ^ l_ {ki} y ^ {l-1} _ {k} + ... w ^ l_ {mi} y ^ {l-1} _ {m} + b ^ l_i \右）} {\ partial w ^ l_ {ki}} = \ delta ^ l_i \ cdot y ^ {l-1} _k \\ && \ forall i \ in（0、...、n）\ enspace \ forall k \ in（0、...、m）\ end {array}$$

分子の合計を展開し、すべての偏微分がゼロに等しいことを取得します $$$\ large \ frac {\ partial w ^ l_ {ki} y ^ {l-1} _ {k}} {\ partial w ^ l_ {ki}}$ それは等しい $$$y ^ {l-1} _k$ 。 このケースは次の場合に発生します $$$k '= k$ 。 バーは、ここで「内部」サイクルを示します $$$k$ 、つまり、これはまったく関連しないイテレータです $$$k$ から $$$\ large \ frac {\ partial E} {\ partial w ^ l_ {ki}}$



そのため、マトリックス形式で表示されます。

$$

$$\ frac {\ partial E} {\ partial w ^ l} = \ left（y ^ {l-1} \ right）^ T \ cdot \ delta ^ l \\ \ tiny（m \ times n）\ enspace \エンスペース\エンスペース（m \回1）\エンスペース\エンスペース（1 \回n）$$

マトリックス次元 $$$y ^ {l-1}$ 等しい $$$（1 \回m）$ 、および行列乗算を生成するには、行列を転置する必要があります。 以下では、マトリックスを完全に「拡張された」形式で表示し、計算がより明確に見えるようにします。

$$

$$\ begin {bmatrix}＆\ frac {\ partial E} {\ partial w ^ {l} _ {00}}＆\ frac {\ partial E} {\ partial w ^ {l} _ {01}}＆。 ..＆\ frac {\ partial E} {\ partial w ^ {l} _ {0n}} \\＆\ frac {\ partial E} {\ partial w ^ {l} _ {10}}＆\ frac { \ partial E} {\ partial w ^ {l} _ {11}}＆...＆\ frac {\ partial E} {\ partial w ^ {l} _ {1n}} \\＆...＆。 ..＆...＆... \\＆\ frac {\ partial E} {\ partial w ^ {l} _ {m0}}＆\ frac {\ partial E} {\ partial w ^ {l} _ {m1}}＆...＆\ frac {\ partial E} {\ partial w ^ {l} _ {mn}} \ end {bmatrix} = \ begin {bmatrix}＆y ^ {l-1} _0 \ delta ^ {l} _0＆y ^ {l-1} _0 \ delta ^ {l} _1＆...＆y ^ {l-1} _0 \ delta ^ {l} _n \\＆y ^ {l- 1} _1 \ delta ^ {l} _0＆y ^ {l-1} _1 \ delta ^ {l} _1＆...＆y ^ {l-1} _1 \ delta ^ {l} _n \\＆。 ..＆...＆...＆... \\＆y ^ {l-1} _m \ delta ^ {l} _0＆y ^ {l-1} _m \ delta ^ {l} _1＆。 ..＆y ^ {l-1} _m \ delta ^ {l} _n \ end {bmatrix} \\ \ qquad \ qquad \ qquad \ qquad \ qquad \ qquad = \ begin {bmatrix}＆y ^ {l-1 } _0 \\＆y ^ {l-1} _1 \\＆... \\＆y ^ {l-1} _m \ end {bmatrix} \ begin {bmatrix}＆\ delta ^ {l} _0＆\ delta ^ {l} _1＆...＆\ delta ^ {l} _n \ end {bmatrix}$$

マトリックスを更新するためのbackprop式の出力 $$$b ^ {l}$

バイアスについては、すべての計算は前の段落と非常に似ています。

$$

$$\ begin {array} {rcl} \ dfrac {\ partial E} {\ partial b ^ l_ {i}}＆=＆\ dfrac {\ partial E} {\ partial y ^ l_i} \ dfrac {\ partial y ^ l_i} {\ partial x ^ l_i} \ dfrac {\ partial x ^ l_i} {\ partial b ^ l_ {i}} = \ delta ^ l_i \ cdot \ dfrac {\ partial x ^ l_i} {\ partial b ^ l_ {i}} \\＆=＆\ delta ^ l_i \ cdot \ dfrac {\ partial \ left（\ sum ^ m_ {k '= 0} w ^ l_ {k'i} y ^ {l-1} _ { k '} + b ^ l_i \ right）} {\ partial b ^ l_ {i}} = \ delta ^ l_i \\ && \ forall i \ in（0、...、n）\ end {array}$$

それは明らかです $$$\ large \ frac {\ partial \ left（\ sum ^ m_ {k '= 0} w ^ l_ {k'i} y ^ {l-1} _ {k'} + b ^ l_i \ right）} { \部分的b ^ l_ {i}} = 1$



マトリックス形式では、すべてが非常に単純です。

$$

$$\ frac {\ partial E} {\ partial b ^ l} = \ delta ^ l \\ \ tiny（1 \ times n）\ enspace \ enspace（1 \ times n）$$

を介した逆プロップ式の導出 $$$y ^ {l-1}$

次の式では、 $$$i$ 各という事実から生じる $$$y ^ {l-1} _k$ それぞれに接続されている $$$x ^ {l} _i$ （レイヤーは完全に接続されていると呼ばれることに注意してください ）

$$

$$\ begin {array} {rcl} \ dfrac {\ partial E} {\ partial y ^ {l-1} _ {k}}＆=＆\ sum_ {i = 0} ^ {n} \ delta ^ l_i \ cdot \ dfrac {\ partial x ^ l_i} {\ partial y ^ {l-1} _ {k}} = \ sum_ {i = 0} ^ {n} \ delta ^ l_i \ cdot \ dfrac {\ partial \ left （\ sum ^ m_ {k '= 0} w ^ l_ {k'i} y ^ {l-1} _ {k'} + b ^ l_i \ right）} {\ partial y ^ {l-1} _ {k}} \\＆=＆\ sum_ {i = 0} ^ {n} \ delta ^ l_i \ cdot \ dfrac {\ partial \ left（w ^ l_ {0i} y ^ {l-1} _ {0 } + \ ldots + w ^ l_ {ki} y ^ {l-1} _ {k} + ... w ^ l_ {mi} y ^ {l-1} _ {m} + b ^ l_i \右） } {\ partial y ^ {l-1} _ {k}} \\＆=＆\ sum_ {i = 0} ^ {n} \ delta ^ l_i \ cdot w ^ l_ {ki} \\ && \ forall i \ in（0、...、n）\ enspace \ forall k \ in（0、...、m）\ end {array}$$

分子を分解すると、すべての偏微分がゼロに等しいことがわかります。ただし、 $$$k '= k$ ：

$$

$$\ frac {\ partial \ left（w ^ l_ {0i} y ^ {l-1} _ {0} + \ ldots + w ^ l_ {ki} y ^ {l-1} _ {k} + .. .w ^ l_ {mi} y ^ {l-1} _ {m} + b ^ l_i \ right）} {\ partial y ^ {l-1} _ {k}} = \ frac {\ partial w ^ l_ {ki} y ^ {l-1} _ {k}} {\ partial y ^ {l-1} _ {k}} = w ^ l_ {ki}$$

そして、マトリックス形式で：

$$

$$\ frac {\ partial E} {\ partial y ^ {l-1}} = \ delta ^ l \ cdot（w ^ l）^ {T} \\ \ tiny（1 \ times m）\ enspace \ enspace \エンスペース（1 \回n）\エンスペース（n \回m）$$

さらに、「オープン」形式のマトリックス。 私は意図的に、転置する前の形で最新の行列のインデックスを残したので、転置後にどの要素がどこに行ったのかを確認した方がよいことに注意してください。

$$

$$\ begin {bmatrix}＆\ frac {\ partial E} {\ partial y ^ {l-1} _ {0}}＆\ frac {\ partial E} {\ partial y ^ {l-1} _ {1 }}＆...＆\ frac {\ partial E} {\ partial y ^ {l-1} _ {m}} \ end {bmatrix} = \\ \ scriptsize \ begin {bmatrix}＆（\ delta ^ { l} _1w ^ {l} _ {00} + \ delta ^ {l} _2w ^ {l} _ {01} + \ ldots + \ delta ^ {l} _nw ^ {l} _ {0n}）＆（\ delta ^ {l} _1w ^ {l} _ {10} + \ delta ^ {l} _2w ^ {l} _ {11} + \ ldots + \ delta ^ {l} _nw ^ {l} _ {1n}）＆。 ..＆（\ delta ^ {l} _1w ^ {l} _ {m0} + \ delta ^ {l} _2w ^ {l} _ {m1} + \ ldots + \ delta ^ {l} _nw ^ {l} _ {mn}）\ end {bmatrix} = \\ \ enspace \ enspace = \ begin {bmatrix}＆\ delta ^ {l} _0＆\ delta ^ {l} _1＆...＆\ delta ^ {l} _n \ end {bmatrix} \ begin {bmatrix}＆w ^ {l} _ {00}＆w ^ {l} _ {01}＆...＆w ^ {l} _ {0n} \\＆w ^ { l} _ {10}＆w ^ {l} _ {11}＆...＆w ^ {l} _ {1n} \\＆...＆...＆...＆... \\ ＆w ^ {l} _ {m0}＆w ^ {l} _ {m1}＆...＆w ^ {l} _ {mn} \ end {bmatrix} ^ T \\ = \ begin {bmatrix}＆ \ delta ^ {l} _0＆\ delta ^ {l} _1＆...＆\ delta ^ {l} _n \ end {bmatrix} \ begin {bmatrix}＆w ^ {l} _ {00}＆w ^ {l} _ {10}＆...＆w ^ {l} _ {m0} \\＆w ^ {l} _ {01}＆w ^ {l} _ {11}＆...＆w ^ {l} _ {m1} \\＆...＆...＆...＆... \\＆w ^ {l} _ {0n}＆w ^ {l} _ {1n}＆...＆w ^ {l} _ {mn} \ end {bmatrix}$$

さらに示す $$$\ large \ frac {\ partial E} {\ partial y ^ {l-1} _ {k}}$ どうやって $$$\ delta ^ {l-1} _k$ 、および完全に接続されたネットワークの後続のレイヤーを介したエラーの逆伝播のすべての式は、同様の方法で計算されます。

maxpoolingによるバックプロップ

エラーは、maxpoolingステップで最大として選択された元のマトリックスの値のみを「通過」します。 マトリックスの残りのエラー値はゼロになります（これらの要素の値は、ネットワークを直接通過する際にmaxpooling関数によって選択されなかったため、最終結果に影響しなかったため、論理的です）。







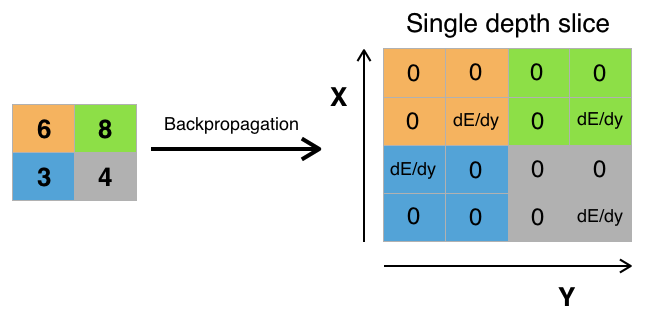
Pythonのmaxpoolingの実装は次のとおりです。





関数が返す2番目の行列は、maxpooling操作中に元の行列から選択された要素の座標です。

畳み込みネットワークを介したバックプロップ

畳み込みカーネルを更新するためのbackprop式の出力

$$

$$\ begin {array} {rcl} \ dfrac {\ partial E} {\ partial w ^ l_ {ab}}＆=＆\ sum_ {i} \ sum_ {j} \ dfrac {\ partial E} {\ partial y ^ l_ {ij}} \ dfrac {\ partial y ^ l_ {ij}} {\ partial x ^ l_ {ij}} \ dfrac {\ partial x ^ l_ {ij}} {\ partial w ^ l_ {ab}} \\＆=＆^ {（1）} \ sum_ {i} \ sum_ {j} \ dfrac {\ partial y} l_ {ij}} \ dfrac {\ partial y ^ l_ {ij}} {\ partial x ^ l_ {ij}} \ cdot \ dfrac {\ partial \ left（\ sum_ {a '=-\ infty} ^ {+ \ infty} \ sum_ {b' =-\ infty} ^ {+ \ infty} w ^ l_ {a'b '} \ cdot y ^ {l-1} _ {（is-a'）（js-b '）} + b ^ l \ right）} {\ partial w ^ l_ { ab}} \\＆=＆^ {（2）} \ sum_ {i} \ sum_ {j} \ dfrac {\ partial E} {\ partial y ^ l_ {ij}} \ dfrac {\ partial y ^ l_ { ij}} {\ partial x ^ l_ {ij}} \ cdot y ^ {l-1} _ {（is-a）（js-b）} \\ && \ forall a \ in（-\ infty、.. 。、+ \ infty）\ enspace \ forall b \ in（-\ infty、...、+ \ infty）\ end {array}$$

（1）ここで、単に式を $$$x ^ l_ {ij}$ なでる $$$a '$ そして $$$b '$ 別のイテレータであることを意味します。

（2）ここで、分子の量を次のようにレイアウトします。 $$$a$ そして $$$b$ ：

$$

$$\ small \ sum_ {i} \ sum_ {j} \ frac {\ partial E} {\ partial y ^ l_ {ij}} \ frac {\ partial y ^ l_ {ij}} {\ partial x ^ l_ {ij }} \ frac {\ partial \ left（w ^ l _ {-\ infty、-\ infty} \ cdot y ^ {l-1} _ {（is + \ infty）（js + \ infty）} + \ ldots + w ^ l_ {ab} \ cdot y ^ {l-1} _ {（is-a）（js-b）} + \ ldots + w ^ l _ {\ infty、\ infty} \ cdot y ^ {l-1} _ {（is- \ infty）（js- \ infty）} + b ^ l \ right）} {\ partial w ^ l_ {ab}}$$

つまり、分子内のすべての偏微分。ただし、 $$$a '= a、b' = b$ ゼロに等しくなります。 同時に $$$\ large \ frac {\ partial w ^ l_ {ab} \ cdot y ^ {l-1} _ {（is-a）（js-b）}} {\ partial w ^ l_ {ab}}$ 等しい $$$y ^ {l-1} _ {（is-a）（js-b）}$



上記のすべてが畳み込みに適用されます。 相互相関のバックプロップ式は、次の場合の符号の変更を除いて似ています $$$a$ そして $$$b$ ：

$$

$$\ frac {\ partial E} {\ partial w ^ l_ {ab}} = \ sum_ {i} \ sum_ {j} \ frac {\ partial E} {\ partial y ^ l_ {ij}} \ frac {\部分的y ^ l_ {ij}} {\部分的x ^ l_ {ij}} \ cdot y ^ {l-1} _ {（is + a）（j + b）}$$

ここで重要なのは、畳み込みカーネル自体が最終式に含まれていないことです。 一種の畳み込み演算がありますが、すでに参加しています $$$\ large \ frac {\ partial E} {\ partial x ^ l_ {ij}}$ そして $$$y ^ {l-1}$ 、およびコアとして機能します $$$\ large \ frac {\ partial E} {\ partial x ^ l_ {ij}}$ 、それでも、特にステップ値が1より大きい場合、畳み込みのようには見えません。 $$$\ large \ frac {\ partial E} {\ partial x ^ l_ {ij}}$ 「破る」 $$$y ^ {l-1}$ 、これは通常の畳み込みに完全には似ていません。 この「崩壊」は、パラメーターが $$$i$ そして $$$j$ 数式のループ内で繰り返します。 デモコードを使用すると、これがすべてどのように見えるかを確認できます。

バイアスの重みを更新するためのバックプロップ式の出力

前の段落と同様に、置換のみ $$$w_ {ab} ^ l$ に $$$b ^ l$ 。 1つの機能マップに1つのバイアスを使用します。

$$

$$\ begin {array} {rcl} \ dfrac {\ partial E} {\ partial b ^ l}＆=＆\ sum_ {i} \ sum_ {j} \ dfrac {\ partial E} {\ partial y ^ l_ { ij}} \ dfrac {\ partial y ^ l_ {ij}} {\ partial x ^ l_ {ij}} \ dfrac {\ partial x ^ l_ {ij}} {\ partial b ^ l} \\＆=＆\ small \ sum_ {i} \ sum_ {j} \ dfrac {\ partial E} {\ partial y ^ l_ {ij}} \ dfrac {\ partial y ^ l_ {ij}} {\ partial x ^ l_ {ij}} \ cdot \ dfrac {\ partial \ left（\ sum_ {a =-\ infty} ^ {+ \ infty} \ sum_ {b =-\ infty} ^ {+ \ infty} w ^ l_ {ab} \ cdot y ^ {l-1} _ {（is-a）（js-b）} + b ^ l \ right）} {\ partial b ^ l} \\＆=＆\ sum_ {i} \ sum_ {j} \ dfrac {\ partial E} {\ partial y ^ l_ {ij}} \ dfrac {\ partial y ^ l_ {ij}} {\ partial x ^ l_ {ij}} \ end {array}$$

つまり、合計をすべてに展開すると $$$i$ そして $$$j$ に関して、すべての偏微分 $$$\部分的なb ^ l$ 1に等しくなります。

$$

$$\ frac {\ partial \ left（\ sum_ {a =-\ infty} ^ {+ \ infty} \ sum_ {b =-\ infty} ^ {+ \ infty} w ^ l_ {ab} \ cdot y ^ { l-1} _ {（is-a）（js-b）} + b ^ l \ right）} {\ partial b ^ l} = 1$$

1枚の標識のカードについては、このカードのすべての要素と「接続」されている1つのバイアスのみ。 したがって、バイアス値を調整するときは、エラーの逆伝播中に取得したマップのすべての値を考慮する必要があります。 別の方法として、このマップ内の要素と同じ数の個別の機能マップにバイアスをかけることができますが、この場合、たたみ込みカーネル自体のパラメーターよりも多くのバイアスパラメーターがあります。 2番目の場合、導関数の計算も簡単です。 $$$\ large \ frac {\ partial E} {\ partial b ^ l_ {ij}}$ （バイアスには既に下付き文字があります $$$ij$ ）それぞれに等しくなります $$$\ large \ frac {\ partial E} {\ partial x ^ l_ {ij}}$ 。

畳み込み層を介してバックプロップ式を導出する

ここでは、すべてが以前の結論に似ています。

$$

$$\ begin {array} {rcl} \ dfrac {\ partial E} {\ partial y ^ {l-1} _ {ij}}＆=＆\ sum_ {i '} \ sum_ {j'} \ dfrac {\部分E} {\部分y ^ l_ {i'j '}} \ dfrac {\部分y ^ l_ {i'j'}} {\部分x ^ l_ {i'j '}} \ dfrac {\部分x ^ l_ {i'j '}} {\ partial y ^ {l-1} _ {ij}} \\＆=＆\ sum_ {i'} \ sum_ {j '} \ dfrac {\ partial E} {\パーシャルy ^ l_ {i'j '}} \ dfrac {\パーシャルy ^ l_ {i'j'}} {\ partial x ^ l_ {i'j '}} \ cdot \ dfrac {\ partial \ left（\ sum_ {a =-\ infty} ^ {+ \ infty} \ sum_ {b =-\ infty} ^ {+ \ infty} w ^ l_ {ab} \ cdot y ^ {l-1} _ {（i's-a ）（j's-b）} + b ^ l \ right）} {\ partial y ^ {l-1} _ {ij}} \\＆=＆\ sum_ {i '} \ sum_ {j'} \ dfrac { \部分E} {\部分y ^ l_ {i'j '}} \ dfrac {\部分y ^ l_ {i'j'}} {\部分x ^ l_ {i'j '}} \ cdot w ^ { l} _ {（i's-i）（j's-j）} \\ && \ forall i、j \次元\エンスペースの行列\エンスペースy ^ {l-1} \ end {array}$$

分子の量を次のようにレイアウトする $$$a$ そして $$$b$ 、すべての偏微分がゼロに等しいことを取得します。ただし、 $$$i's-a = i$ そして $$$j's-b = j$ 、それに応じて、 $$$a = i's-i$ 、 $$$b = j's-j$ 。 これは畳み込みにのみ当てはまり、相互相関は $$$i's + a = i$ そして $$$j's + b = j$ それに応じて $$$a = i-iの$ そして $$$b = j-jの$ 。 そして、相互相関の場合の最終的な式は次のようになります。

$$

$$\ frac {\ partial E} {\ partial y ^ {l-1} _ {ij}} = \ sum_ {i '} \ sum_ {j'} \ frac {\ partial E} {\ partial y ^ l_ { i'j '}} \ frac {\ partial y ^ l_ {i'j'}} {\ partial x ^ l_ {i'j '}} \ cdot w ^ {l} _ {（i-i's）（j -j's）}$$

結果の式は同じ畳み込み演算で、カーネルはおなじみのカーネルです $$$w ^ l$ 。 しかし、真実、すべてが通常の畳み込みのように見えますが、ストライドが1に等しい場合のみ、別のステップの場合、他のものが既に取得されています（畳み込みカーネルを更新するためのbackpropの場合と同様） $$$w ^ l$ マトリックス全体で「破壊」し始める $$$\ large \ frac {\ partial E} {\ partial x ^ l}$ さまざまな部分をキャプチャします（これも、インデックスが $$$i '$ そして $$$j '$ で $$$w ^ l$ 数式のループ内で繰り返されます）。



ここで、コードを確認してテストできます。





興味深いことに、相互相関を実行する場合、ネットワークを直接通過する段階で、畳み込みコアは反転せず、畳み込み層を介してエラーが逆方向に伝搬するときに反転します。 畳み込み式を適用すると、すべてがまったく逆になります。



この記事では、エラーの逆伝播のすべての式、つまり、将来のモデルが学習できる式を導き出し、詳細に調べました。 次の記事では、これをすべて畳み込みネットワークと呼ばれる単一のコードに結合し、このネットワークをトレーニングして実際のデータセットのクラスを予測します。 また、テンソルフロー機械学習ライブラリと比較して、すべての計算が正しいことを確認します。