SNARKの説明。 計算から多項式、Pinocchioプロトコルおよび楕円曲線のペアリング（翻訳）

こんにちは、Habr！ ZCashのブログ記事の翻訳を紹介します。この記事では、ZCash暗号通貨で使用されるゼロ開示証拠システムSNARKの動作メカニズムについて説明しています（これだけではありません）。



ソース： https : //z.cash/blog/snark-explain5.html



前の記事：



パート1： SNARKの説明。 準同型隠蔽とブラインド多項式計算（翻訳）

パート2： SNARKの説明。 採用された係数の知識と信頼できる多項式のブラインド計算（翻訳）

翻訳者からの紹介

翻訳の最後の部分から始めて、私たちは本当に素晴らしい時間に住んでいると言いたいです。 高度な数学がソフトウェア開発にほとんどすぐに関与する機会があり、ブロックチェーンとデータ交換に基づいた高度なもので、技術機関の数学者の仕事の結果を「実際に」観察することができます。



さて、私はあなたの注意をこれ以上遅らせません、最も興味深いものに移りましょう...

計算から多項式へ

以前の記事では、多項式を扱うための特定のメカニズムを開発しました。 このパートでは、証明し、検証したいステートメントを多項式の言語で変換する方法を学びます。 このように多項式を使用するというアイデアは、1991年のルンド、フォートウォン、カルロフ、およびニサン（カールステンルンド、ランスフォートノウ、ハワードカルロフ-シカゴ大学およびノアムニサン-ヘブライ大学） による画期的な作業から始まります。



2013年には、ジェンナロ、ジェントリー、パルノ、ライコバ（ロサリオジェンナロ、クレイグジェントリー、ブライアンパルノ、マリアナレイコバ）によって、 さらに別の画期的な作品が発表されました。 この研究により、計算から2次算術プログラム（QAP）と呼ばれる多項式への非常に便利な変換が特定されました。 KAPはzk-SNARKの最新の設計、特にZCash暗号通貨で使用される設計の基礎となっています。



記事の最初の部分では、例を使用してCAPでの計算の変換について説明します。 一般的な定義ではなく小さな例に焦点を合わせたとしても、最初にそれを理解するには十分な時間を費やす必要があります。 精神的な努力に備えてください:)



アリスがボブに知っていることを証明したいとします $$$c_1、c_2、c_3∈F_p$ そのような $$$（c_1⋅c_2）⋅（c_1 + c_3）= 7$ 。 最初のステップは、計算を表示することです $$$c_1、c_2、c_3$ 算術図の形で。

算術図

算術スキームは、加算や乗算などの遷移と呼ばれる計算演算と、それらの間の接続で構成されます。 この場合、スキームは次のようになります。





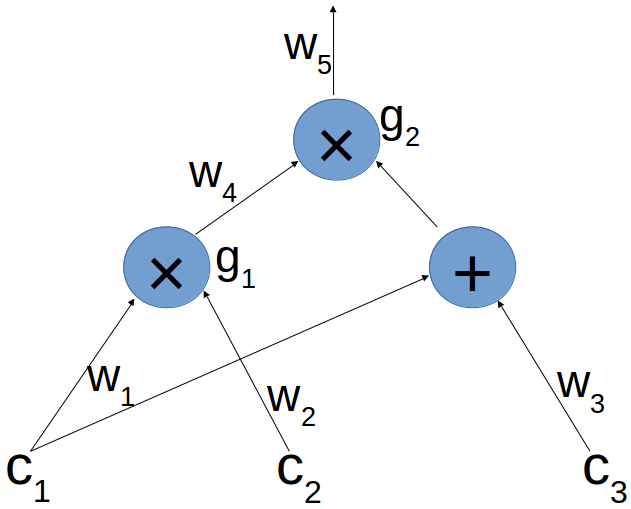
下部のコネクタは入力パラメータであり、上部の出力接続はこれらの入力パラメータの回路全体を計算した結果です。



図からわかるように、回路のコネクタと遷移は特定の方法で示されています。 これらのルールは、次のステップ、つまりスキームをCAPに転送するために必要になります。

• 同じ発信コネクタが複数の遷移に入る場合、それは同じコネクタであると見なされます-たとえば、 $$$w_1$ 例では。
• 乗算ブロックには、左右のコネクタと呼ばれる2つの入力があります。
• 加算から乗算または加算に進むコネクターはマークされません。 加算遷移の入力パラメーターは乗算遷移に直接進むと考えられています。 この例では、 $$$w_1$ そして $$$w_3$ 入力です $$$g_2$

回路の有効な割り当てセットは、ラベル付き遷移の値の割り当てです。各乗算遷移の出力値は、対応する入力の積の結果です。



したがって、このスキームでは、有効な割り当てのセットの形式は次のとおりです。 $$$（c_1、...、c_5）$ どこで $$$c_4 =c_1⋅c_2$ そして $$$c_5 =c_4⋅（c_1 + c_3）$



この用語に従って、アリスは有効な割り当てセットを知っていることを証明したい $$$（c_1、...、c_5）$ そのような $$$c_5 = 7$ 。 次のステップは、CAPを使用してこのステートメントを多項式に変換することです。

CAPにキャスト

乗算の各遷移は、フィールドの要素と相関する必要があります。 $$$g_1$ と相関します $$$1∈F_p$ そして $$$g_2$ と $$$2∈F_p$ 。 ポイント{1、2}を ターゲットポイントと呼びます。 次に、「左接続多項式」のセットを定義する必要があります $$$L_1、...、L_5$ 、「右接続多項式」 $$$R_1、...、R_5$ および「出力接続多項式」 $$$O_1、...、O_5$ 。



このアクションの主な考え方は、多項式の値は、それらが関与する乗算の​​ターゲット遷移点を除き、すべてのターゲット点でゼロに等しいということです。



具体的には、 $$$w_1、w_2、w_4$ それぞれ、左、右、および出力コネクタ $$$g_1$ 決定できる $$$L_1 = R_2 = O_4 = 2-X$ 多項式 $$$2-X$ 対応するポイント1で1に等しい $$$g_1$ 対応するポイント2でゼロに等しい $$$g_2$ 。



に注意してください $$$w_1$ そして $$$w_3$ どちらも正しい入力です $$$g_2$ 。 したがって、同様に定義します $$$L_4 = R_1 = R_3 = O_5 = X- 1$ 以来 $$$X- 1$ 対応するターゲットポイント2の 1に等しい $$$g_2$ 別のターゲットポイントでゼロ。



他のすべての多項式をゼロ多項式として示します。



固定値の場合 $$$（c_1、...、c_5）$ これらは、左、右、および出力「合計」多項式を決定するための係数として使用されます。 つまり、以下を決定できます。



$$ $インライン$ L：=Σ^ 5_ {i = 1}c_i⋅L_i、R：=Σ^ 5_ {i = 1}c_i⋅R_i、O：=Σ^ 5_ {i = 1}c_i⋅O_i$ inline $



次に、多項式を定義します $$$P：= L⋅R-O$



さて、これらすべての定義の後、中心的な定義を定式化できます。 $$$（c_1、...、c_5）$ Pがすべてのターゲットポイントでゼロの値をとる場合にのみ、有効なスキーム割り当てセットです。



この例を使用して、これを確認しましょう。 定義されたとします $$$L、R、O、P$ 上記のように $$$c_1、...、c_5$ 。 これらすべての多項式をターゲットポイント1で計算してみましょう。



すべての $$$L_i$ のみ $$$L_1$ ポイント1で非ゼロ。 だから $$$L（1）=c_1⋅L_1（1）= c_1$ 。 同様に、以下を取得します $$$R（1）= c_2$ そして $$$O（1）= c_4$ 。



だから $$$P（1）=c_1⋅c_2- c_4$ 。 あなたは同様のものを得ることができます $$$P（2）=c_4⋅（c_1 + c_3）-c_5$ 。



言い換えれば、 Pは、以下の場合にのみ、ターゲットポイントで消滅します。 $$$（c_1、...、c_5）$ 有効な割り当てセットです。



ここで、次の代数的事実を使用します。多項式Pと点 $$$a∈F_p$ 、私たちは持っています $$$P（a）= 0$ 多項式の場合 $$$X-a$ Pを剰余なしで除算する、すなわち $$$P =（X- a）⋅H$ 多項式Hについて



この方法でターゲット多項式を定義すると： $$$T（X）：=（X- 1）⋅（X- 2）$ 、次の場合にのみTがPを分割することがわかります。 $$$（c_1、...、c_5）$ 有効な割り当てセットです。



上記に基づいて、KAPを次のように定義します。



次数dおよびサイズmの2次算術プログラムQは、多項式で構成されます $$$L_1、...、L_m、R_1、...、R_m、O_1、...、O_m$ および次数dのターゲット多項式T。



割り当てセット $$$（c_1、...、c_m）$ Qを 満たす場合、定義 $$ $インライン$ L：=Σ^ m_ {i = 1} c_i⋅L_i、R：=Σ^ m_ {i = 1}c_i⋅R_i、O：=Σ^ m_ {i = 1}c_i⋅O_i $ inline $ そして $$$P：= L⋅R-O$ 、剰余Pなしで分割するTが存在します。



この用語に従って、アリスは割り当てセットを知っていることを証明したい $$$（c_1、...、c_5）$ 上記で定義されたCAPを満たします。 $$$c_5 = 7$ 、



この部分を要約します。 「知ってるよ $$$c_1、c_2、c_3$ そのような $$$（s_1⋅c_2）⋅（c_1 + c_3）= 7$ »KAPを使用して、多項式に関する同等のステートメントに変換できます。 次に、KAPの有効な割り当てセットの知識を確認するための効果的なプロトコルを検討します。

上記では、KAPにキャストするかなり短い例を示しました。 プログラムをKAPに変換する方法の詳細については、 Vitalik Buterinの優れた投稿もお勧めします。

ピノキオプロトコル

アリスがボブに証明したいステートメントは、二次算術プログラム（CAP）と呼ばれる「多項式言語」の同等の形式に変換できることを以前に示しました。



このパートでは、Aliceがかなり短い証明をBobに送信し、KAPに有効な割り当てセットがあることを示す方法を説明します。 パルノ、ハウエル、ジェントリー、ライコバが開発したピノキオプロトコル （ブライアンパルノ、ジョンハウエル、クレイグジェントリー、マリアナレイコバ）を使用します。



上記のように、アリスは、追加の制限がある有効な割り当てセットがあることを証明したいと考えています。たとえば、 $$$c_m = 7$ 。 ただし、ここではこれを考慮せず、簡単にするために、許容される割り当てのセットの知識を証明することがいかに簡単かを示します。



Aliceに有効な割り当てセットがある場合、つまり、定義する場合 $$$L、R、O、P$ 上記のように、次のような多項式Hが存在します。 $$$P =H⋅T$ 。 特に、 $$$s∈F_p$ 私たちは持っています $$$P（s）= H（s）⋅T（s）$ 。



ここで、アリスには有効な割り当てセットがありませんが、彼女は $$$L、R、O、P$ 無効なセットから $$$（c_1、...、c_m）$ 。 そうすれば、 TがPを分割しないことが確実になります。 これは、最大でd 、 Pおよび $$$H⋅T$ 異なる多項式になります。 Pと $$$H⋅T$ ここに高次の順序はありません $$$2d$ 。



これを証明するために、 よく知られた Schwarz-Zippel補題を使用します。 $$$2d$ 以下と交差することはできません $$$2d$ ポイント $$$s∈F_p$ 。 したがって、 pがはるかに大きい場合 $$$2d$ その可能性 $$$P（s）= H（s）⋅T（s）$ ランダム選択用 $$$s∈F_p$ 取るに足らない。



これに基づいて、次のプロトコルスケッチを作成して、アリスに有効な割り当てセットがあるかどうかを確認できます。

1. アリスは多項式を選ぶ $$$L、R、O、H$ d以下の次数
2. ボブはランダムなポイントを選びます $$$s∈F_p$ そして非表示を計算します $$$E（T（s））$ 。
3. アリスは、ポイントsでこれらの多項式の非表示をボブに送信します。 $$$E（L（s））、E（R（s））、E（O（s））、E（H（s））$ 。
4. ボブは、必要な平等がsで保持されるかどうかを確認します。 つまり、彼はチェックします $$$E（L（s）⋅R（s）−O（s））= E（T（s）⋅H（s））$

繰り返しますが、アリスが有効な割り当てセットを持っていない場合、最終的には、ほとんどのランダムに選択されたsに必要な等式が成り立たない多項式を使用します。 したがって、ボブは、選択されたsに関係なく、アリスの応答を拒否する可能性があります。



このスケッチを実装するツールはありますか？ 重要な点は、アリスがsを知らなくても使用する多項式の選択です。 しかし、これはまさに、 前の記事で説明した多項式の信頼できるブラインド計算で解決した問題です。



これを考えると、このスケッチをzk-SNARKに変えるために解決する必要がある4つのキーポイントがあります。 この記事のフレームワークで最初の2つを検討し、最後の記事で他の2つを検討します。

アリスが割り当てセットに従って多項式を選択するという確信

重要な点：アリスに有効な割り当てセットがない場合、これは彼女が多項式を見つけられないという意味ではありません $$$L、R、O、H$ d以下の次数 $$$L⋅R-O =T⋅H$ 。 それは、彼女がそのような多項式を見つけることができないことを意味します $$$L、R$ そして $$$O$ 「割り当てセットから派生した」; つまり $$ $インライン$ L：=Σ^ m_ {i = 1}c_i⋅L_i、R：=Σ^ m_ {i = 1}c_i⋅R_i、O：=Σ^ m_ {i = 1}c_i⋅O_i $ inline $ ダイヤル用 $$$（c_1、...、c_m）$ 。



上記のプロトコルは、いくつかの多項式を使用することのみを保証します $$$L、R、O$ 望ましい順序ですが、有効な割り当てセットから作成されたことを保証するものではありません。 正式な証明には多少注意が必要なので、おおよその解決策を示します。



互換性のある多項式をみましょう $$$L、R、O$ 次のように1つの多項式Fに ：



$$$F = L + X ^ {d + 1}⋅R + X ^ {2（d + 1）}⋅O$



Rに乗算する意味 $$$X ^ {d + 1}$ そして、 O $$$X ^ {2（d + 1）}$ 比率を混ぜない $$$L、R、O$ fで 。 オッズ $$$1、X、...、X ^ d$ FではLに対応し、次の $$$d + 1$ 係数 $$$X ^ {d + 1}、...、X ^ {2（d + 1）}$ Rに対応し、後者 $$$d + 1$ 係数はOに対応します。



同様にCAPの定義内の多項式を組み合わせ、それぞれに対して定義します $$$i∈{1、...、m}$ 多項式 $$$F_i$ その最初の $$$d + 1$ 係数は係数です $$$L_i$ そしてオッズ $$$R_i$ そして $$$O_i$ 。 つまり、それぞれの $$$i∈{1、...、m}$ 多項式を定義します：



$$$F_i = L_i + X ^ {d + 1}⋅R_i + X ^ {2（d + 1）}⋅O_i$



2つを合計すると $$$F_i$ それから $$$L_i、R_i$ そして $$$O_i$ 「個別に要約されています。」 例えば $$$F_1 + F_2 =（L_1 + L_2）+ X ^ {d + 1}⋅（R_1 + R_2）+ X ^ {2（d + 1）}⋅（O_1 + O_2）$ 。



より一般的には、 $$$F =Σ^ m_ {i = 1}c_i⋅F_i$ いくつかのセット $$$（c_1、...、c_m）$ 。 それからまた私達は得る $$ $インライン$ L =Σ^ m_ {i = 1}c_i⋅L_i、R =Σ^ m_ {i = 1}c_i⋅R_i、O =Σ^ m_ {i = 1}c_i⋅O_i $ inline $ 同じ比率で $$$（c_1、...、c_m）$ 。 つまり、 Fが線形結合の場合 $$$F_i$ つまり $$$L、R、O$ 実際にセットから作成されました。



したがって、ボブはアリスに、 Fが次の線形結合であることを証明するように依頼します。 $$$F_i$ 。 これは、信頼できる計算のためのプロトコルと同様に行われます。



ボブはランダムに選ぶ $$$β∈F ^ * _ p$ 、およびアリスに非表示を送信します $$ $インライン$ E（β⋅F_1（s））、...、E（β⋅F_m（s））$ inline $ 。 それから彼はアリスに彼に皮を送るよう頼む $$$E（β⋅F（s））$ 。 彼女が成功した場合、受け入れられたオッズに関する知識の高度なバージョンは、彼女がFの作成方法を知っていると仮定します。 $$$F_i$ 。

「ゼロディスクロージャー」パーツの追加-割り当てセットの非表示

zk-SNARKでは、アリスは自分の割り当てセットに関するすべての情報を非表示にしたいと考えています。 しかし隠れている $$$E（L（s））、E（R（s））、E（O（s））、E（H（s）$ いくつかのセット情報を提供します。



たとえば、他の満足のいく割り当てセットがある場合 $$$（c'_1、...、c'_m）$ ボブは適切な $$$L '、R'、O '、H'$ 隠れている $$$E（L '（s））、E（R'（s））、E（O '（s））、E（H'（s））$ 。 それらがアリスの答えと異なる場合、彼はそれを理解することができます $$$（c'_1、...、c'_m）$ アリスの割り当てセットではありません。



このようなセットに関する情報の漏洩を回避するために、アリスは各多項式に「ランダムTシフト」を追加することでセットを隠します。 ランダムを選択します $$ $インライン$δ_1、δ_2、δ_3∈F ^ * _ p $インライン$ 、および定義 $$ $インライン$ L_z：= L +δ_1⋅T、R_z：= R +δ_2⋅T、O_z：= O +δ_3⋅T $ inline $ 。



と仮定する $$$L、R、O$ 満足できる割り当てセットから取得されました。 だから $$$L⋅R-O =T⋅H$ 多項式Hについて どこでもTの倍数を追加したので、 Tも分割します $$$L_z⋅R_z- O_z$ 。 これを確認しましょう：



$$ $インライン$L_z⋅R_z- O_z =（L +δ_1⋅T）（R +δ_2⋅T）-（O +δ_3⋅T）$インライン$ $$ $ inline $ =（L⋅R-O）+ L⋅δ_2⋅T +δ_1⋅T⋅R +δ_1δ_2⋅T ^ 2-δ_3⋅T $ inline $ $$ $インライン$ =T⋅（H + L⋅δ_2+δ_1⋅R +δ_1δ_2⋅T-δ_3）$インライン$



したがって、定義 $$ $インライン$ H_z = H + Lδδ_2+δ_1⋅R +δ_1δ_2⋅T-δ_3$インライン$ 私たちは得る $$$L_z⋅R_z- O_z =T⋅H_z$ 。 したがって、アリスが多項式を使用する場合 $$$L_z、R_z、O_z、H_z$ の代わりに $$$L、R、O、H$ ボブは常に答えを受け入れます。



一方、これらの多項式は $$$s∈F_p$ を提供する $$$T（s）≠0$ （ほとんどすべてのdおよびsに当てはまります ）、有効な割り当てセットに関する情報を含めないでください。 例えば $$$T（s）$ ゼロとは異なり、 $$$δ_1$ ランダムです。 それから $$$δ_1⋅T（s）$ ランダムな値なので、 $$$L_z（s）= L（s）+δ_1⋅T（s）$ についての情報は含まれません $$$L（s）$ このランダムな値によって「マスク」されているためです。

最後の部分で考慮すべきことは何ですか？

アリスがボブにKAPの有効な割り当てセットを持っていることを説得し、このセットに関する情報を公開することなくピノキオプロトコルスキームを大まかに示しました。 しかし、zk-SNARKを取得するために解決する必要がある2つの重要な問題があります。

• このスキームでは、ボブは多項式Hを必要とします。これは「乗算をサポートします」。 たとえば、彼は非表示を計算する必要があります $$$E（H（s）⋅T（s））$ から $$$E（H（s））$ そして $$$E（T（s））$ 。 ただし、これを可能にするHの例はまだ検討していません。 加算と線形結合をサポートするHのみを考慮しました。
• また、アリスとボブの間のインタラクティブプロトコルについても説明しました。 ただし、最終的な目標は、アリスが1つのメッセージで非インタラクティブな証拠を送信できるようにすることです。 これらのメッセージは公開されています。 これは、この「メッセージは証拠である」とわかる人は誰でも、ボブ（以前にアリスとやり取りした）だけでなく、その信頼性も確信できることを意味します。

これらの問題は両方とも、楕円曲線のペアを使用して解決できます。これについては、最終パートで説明します。



次の記事： SNARKの説明。 楕円曲線のペアリング（翻訳）