この記事では、機械学習の生成モデルに関するシリーズを開始しています。 機械学習の古典的な問題を見て、生成モデリングとは何かを定義し、機械学習の古典的な問題との違いを見て、この問題を解決するための既存のアプローチを見て、ディープニューラルネットワークの学習に基づくアプローチの詳細に飛び込みます。 しかし、最初に、序論として、確率的設定における機械学習の古典的な問題に注目します。
古典的な機械学習の課題
2つの古典的な機械学習タスクは、分類と回帰です。 それぞれを詳しく見てみましょう。 両方の問題の定式化とその解決策の最も単純な例を考えてみましょう。
分類
分類タスクは、ラベルをオブジェクトに割り当てるタスクです。 たとえば、オブジェクトが写真である場合、タグは写真の内容である可能性があります。画像に歩行者が含まれているかどうか、男性または女性が描かれているか、犬の犬種が写真に描かれているかなどです。 通常、相互に排他的なラベルのセットと、これらのラベルが知られているオブジェクトのコレクションがあります。 このようなデータのコレクションがあるため、元のコレクションにあった同じタイプの任意のオブジェクトにラベルを自動的に配置する必要があります。 この定義を形式化しましょう。
多くのオブジェクトがあるとしましょう 。 飛行機のポイント、手書きの数字、写真、音楽作品などです。 また、ラベルの有限セットがあると仮定します
。 これらのタグには番号を付けることができます。 タグとその番号を特定します。 このように
私たちの表記では
。 もし
、その後、タスクはバイナリ分類問題と呼ばれ、3つ以上のラベルがある場合、彼らは通常、これは単なる分類問題であると言います。 さらに、入力サンプルがあります
。 これらは、タグを自動的に配置する方法を学習する非常に顕著な例です。 すべてのオブジェクトのクラスを正確に知っているわけではないため、オブジェクトのクラスはランダム変数であると信じています。
。 たとえば、犬の写真は、0.99の確率で犬として、0.01の確率で猫として分類できます。 したがって、オブジェクトを分類するには、このオブジェクト上のこのランダム変数の条件付き分布を知る必要があります
。
見つけるタスク ラベルの特定のセットに対して
このタグ付きサンプルのセット
分類問題と呼ばれます。
分類問題の確率的ステートメント
この問題を解決するには、確率論的言語で再定式化すると便利です。 だから多くのオブジェクトがあります そして多くのタグ
。
からのランダムなオブジェクトを表すランダム変数です
。
からのランダムなラベルを表すランダム変数です
。 ランダム変数を考えます
配布あり
、オブジェクトとそのクラスの共同分布です。 次に、サンプリングされたサンプルは、この分布からのサンプルです。
。 すべてのサンプルが独立して均等に分布していると仮定します(英語の文献ではiid)。
分類問題は、発見の問題として再定式化できるようになりました このサンプルで
。
2つの正規分布の分類
簡単な例でこれがどのように機能するかを見てみましょう。 置く 、
、
、
、
。 つまり、2つのガウス分布があり、そのうちデータをサンプリングする可能性が等しく、必要な点は
、どのガウス分布から派生したかを予測します。
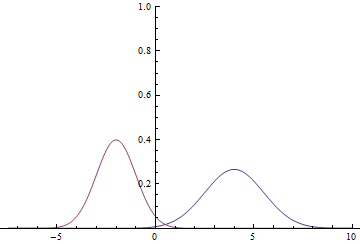
図 1.分布密度 そして
。
ガウス領域は数値線全体であるため、これらのグラフが交差することは明らかです。つまり、確率密度が そして
等しいです。
クラスの条件付き確率を見つける:
すなわち
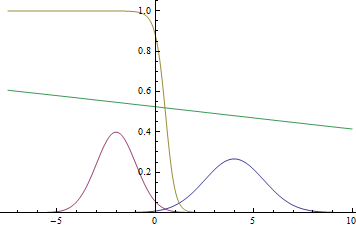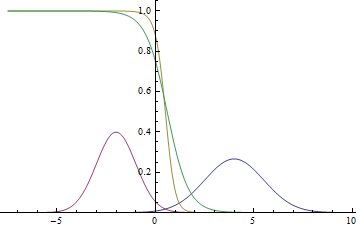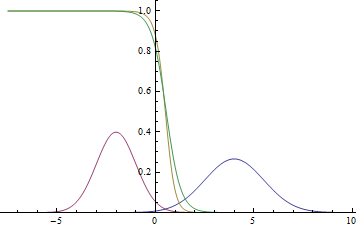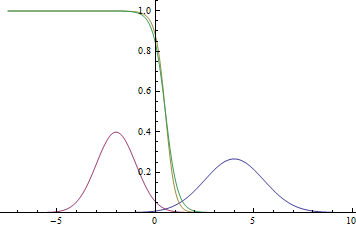
これは、確率密度グラフがどのように見えるかです :
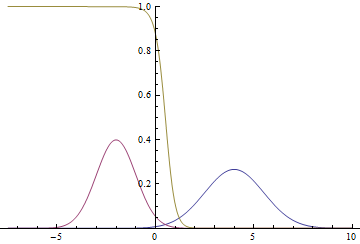
図 2.分布密度 、
そして
。
2つのガウス分布が交差する場所。
ガウスモードに近く、ポイントが特定のクラスに属するという事実におけるモデルの信頼性が非常に高く(確率がゼロまたは1に近い)、グラフが交差する場所では、モデルが推測して与えることができることがわかります。 。
信頼性最大化方法
実際の問題のほとんどは、上記の方法では解決できません。 通常、明示的に指定されていません。 代わりに、通常はデータセットがあります
いくつかの未知の共同分布密度
。 この場合、 最尤法を使用して問題を解決します。 メソッドの正式な定義と正当化は、統計に関するお気に入りの本または上記のリンクで見つけることができます。この記事では、その直感的な意味を説明します。
尤度最大化の原理では、未知の分布がある場合 そこからサンプルのセットがあります
、いくつかの有名なパラメトリック分布群
するために
できるだけ近い
、あなたはそのようなパラメータのベクトルを見つける必要があります
データの結合確率を最大化する(尤度)
、データの尤度とも呼ばれます。 合理的な条件下では、この推定値は、パラメーターの真のベクトルの一貫した偏りのない推定値であることが証明されています。 サンプルが選択された場合
、つまりiidデータの場合、共同分布は分布の積に分割されます。
対数と定数の乗算は単調に増加する関数であり、最大値の位置は変更されません。したがって、ジョイント密度は対数の下に導入され、乗算されます :
最後の式は、予想尤度対数の公平で一貫した推定です。
最大化問題は、最小化問題として書き直すことができます。
後者の量は、分布のクロスエントロピーと呼ばれます。 そして
。 強化を伴うトレーニング(教師あり学習)の問題を解決するために最適化することが彼女の習慣です。
このシリーズの記事では、 確率的勾配降下法(SGD)を使用して最小化を実行します。または、サブサンプルの勾配の合計(いわゆる「ミニバッチ」)が最小化された関数の勾配の不偏推定値であるという事実を利用して、適応モーメントに基づいた拡張を行います。
ロジスティック回帰による2つの正規分布の分類
パラメトリックファミリとして、最尤法を使用して、上記と同じ問題を解決してみましょう。 最も単純なニューラルネットワーク。 結果のモデルは、ロジスティック回帰と呼ばれます。 完全なモデルコードは、 ここで見つけることができます。記事では、キーポイントのみが強調表示されています。
まず、トレーニング用のデータを生成する必要があります。 クラスラベルのミニバッチを生成し、各ラベルが対応するガウスからポイントを生成する必要があります。
def input_batch(dataset_params, batch_size): input_mean = tf.constant(dataset_params.input_mean, dtype=tf.float32) input_stddev = tf.constant(dataset_params.input_stddev,dtype=tf.float32) count = len(dataset_params.input_mean) labels = tf.contrib.distributions.Categorical(probs=[1./count] * count) .sample(sample_shape=[batch_size]) components = [] for i in range(batch_size): components .append(tf.contrib.distributions.Normal( loc=input_mean[labels[i]], scale=input_stddev[labels[i]]) .sample(sample_shape=[1])) samples = tf.concat(components, 0) return labels, samples
分類子を定義します。 隠れ層のない最も単純なニューラルネットワークになります。
def discriminator(input): output_size = 1 param1 = tf.get_variable( "weights", initializer=tf.truncated_normal([output_size], stddev=0.1) ) param2 = tf.get_variable( "biases", initializer=tf.constant(0.1, shape=[output_size]) ) return input * param1 + param2
そして、損失関数を書きます-実ラベルと予測ラベルの分布間のクロスエントロピー:
labels, samples = input_batch(dataset_params, training_params.batch_size) predicted_labels = discriminator(samples) loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits( labels=tf.cast(labels, tf.float32), logits=predicted_labels) )
以下は、2つのモデルのトレーニングスケジュールです:基本モデルとL2正規化あり:
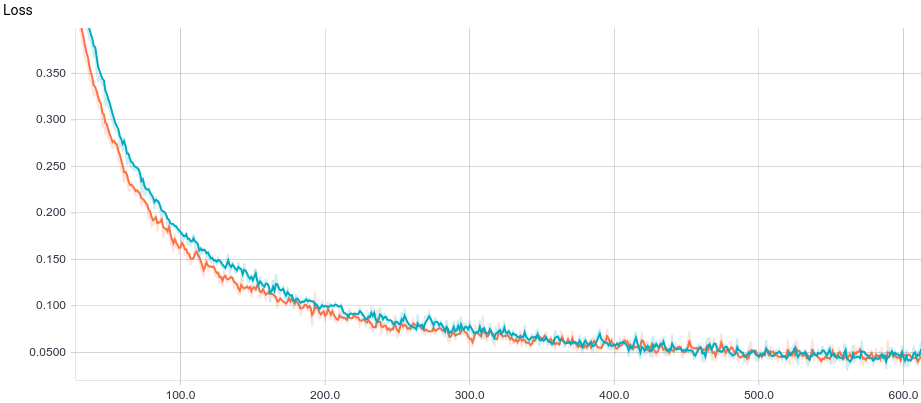
図 3.ロジスティック回帰の学習曲線。
両方のモデルがすぐに良好な結果に収束することがわかります。 正則化のないモデルは、このタスクでは正則化が必要ないため、より良く表示され、学習速度がわずかに遅くなります。 学習プロセスを詳しく見てみましょう。

図 4.ロジスティック回帰の学習プロセス。
訓練された分離面は、解析的に計算されたものに徐々に収束し、損失関数の勾配が弱いため収束が遅くなることがわかります。
回帰
回帰問題は、1つの連続確率変数を予測するタスクです 他のランダム変数の値に基づいて
。 たとえば、性別(離散確率変数)と年齢(連続確率変数)に応じて、人の成長を予測します。 分類問題と同じ方法で、ラベル付きサンプルが与えられます
。 ランダム変数はランダムであり、実際には関数であるため、ランダム変数の値を予測することは直接不可能です。したがって、正式にはタスクは条件付き期待値の予測として記述されます。
通常のノイズを伴う線形依存値の回帰
簡単な例を使用して、回帰問題がどのように解決されるかを見てみましょう。 2つの独立したランダム変数があるとします 。 たとえば、これは木の高さと通常のランダムノイズです。 次に、木の年齢はランダム変数であると仮定できます。
。 この場合、数学的期待と独立性の線形性
そして
:
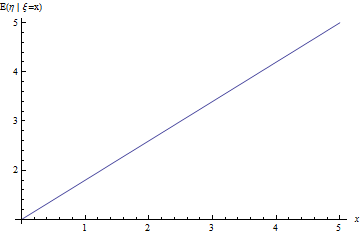
図 5.問題の回帰直線は、ノイズを伴う線形依存量です。
最尤回帰問題の解
最尤法により回帰問題を定式化しましょう。 置く ) どこで
-パラメータの新しいベクトル。 探しているものを見る
-期待
、つまり これは、正しいポーズの回帰問題です。 それから
この期待値の有効で公平な推定値は、サンプルの平均になります
したがって、回帰問題を解決するには、トレーニングセットの平均二乗誤差を最小化すると便利です。
線形回帰による値の回帰
パラメトリックファミリとして、前のセクションの方法を使用して、上記と同じ問題を解決してみましょう。 最も単純なニューラルネットワーク。 結果のモデルは線形回帰と呼ばれます。 完全なモデルコードは、 ここで見つけることができます。記事では、キーポイントのみが強調表示されています。
まず、トレーニング用のデータを生成する必要があります。 まず、入力変数のミニバッチを生成します 、その後、ソース変数のサンプルを取得します
:
def input_batch(dataset_params, batch_size): samples = tf.random_uniform([batch_size], 0., 10.) noise = tf.random_normal([batch_size], mean=0., stddev=1.) labels = (dataset_params.input_param1 * samples + dataset_params.input_param2 + noise) return labels, samples
モデルを定義します。 隠れ層のない最も単純なニューラルネットワークになります。
def predicted_labels(input): output_size = 1 param1 = tf.get_variable( "weights", initializer=tf.truncated_normal([output_size], stddev=0.1) ) param2 = tf.get_variable( "biases", initializer=tf.constant(0.1, shape=[output_size]) ) return input * param1 + param2
そして、損失関数-実数値と予測値の分布間のL2距離を記述します。
labels, samples = input_batch(dataset_params, training_params.batch_size) predicted_labels = discriminator(samples) loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits( labels=tf.cast(labels, tf.float32), logits=predicted_labels) )
以下は、2つのモデルのトレーニングスケジュールです:基本モデルとL2正規化あり:

図 6.線形回帰の学習曲線。
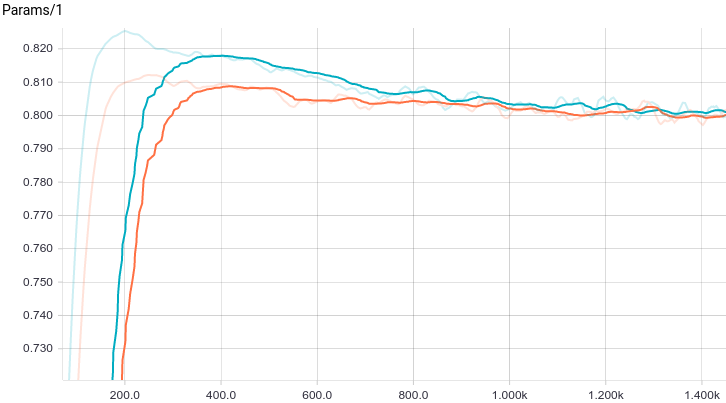
図 7.トレーニングステップでの最初のパラメーターの変更のスケジュール。
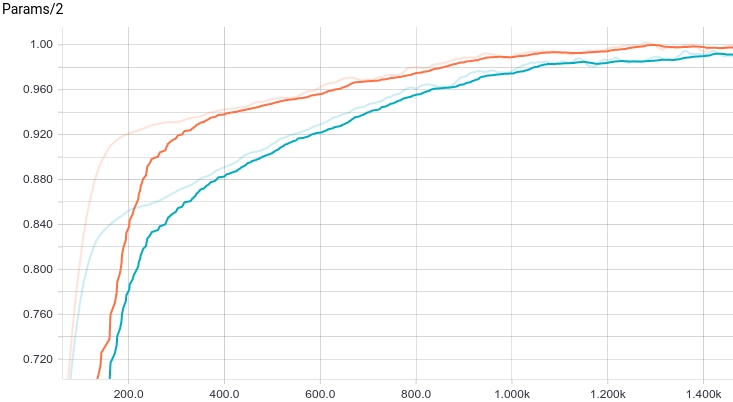
図 8.トレーニングステップでの2番目のパラメーターの変更のスケジュール。
両方のモデルがすぐに良好な結果に収束することがわかります。 正則化のないモデルは、このタスクでは正則化が必要ないため、より良く表示され、学習速度がわずかに遅くなります。 学習プロセスを詳しく見てみましょう。
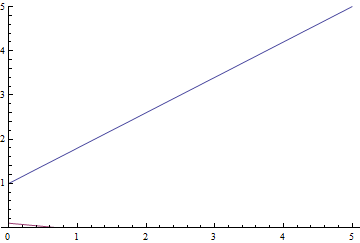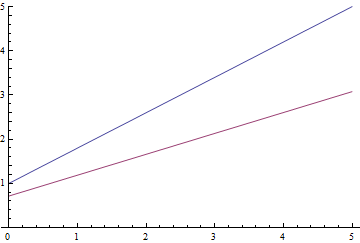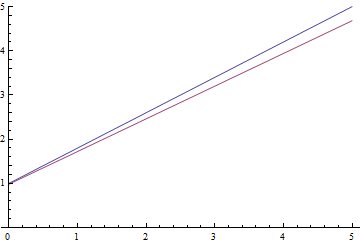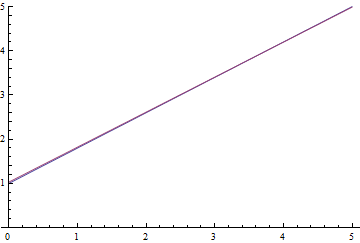
図 9.線形回帰を学習するプロセス。
予想される数学的期待値は 解析的に計算されたものに徐々に収束し、さらに、それが近いほど、損失関数の勾配がますます弱くなるため収束が遅くなります。
その他のタスク
上記で検討した分類および回帰の問題に加えて、教師とのいわゆるトレーニングには他のタスクがあります。これは主にポイントとシーケンス間のマッピングに帰着します:オブジェクトからシーケンス、シーケンスからシーケンス、シーケンスからオブジェクト。 また、教師なしで教える古典的な問題も幅広くあります。クラスタリング、データギャップの埋め方、そして最後に、生成モデリングに使用される分布の明示的または暗黙的な近似です。 この一連の記事で説明するのは、最後のクラスの問題についてです。
生成モデル
次の章では、生成モデルとは何か、それらがこの章で説明した判別モデルとどのように根本的に異なるかを見ていきます。 生成モデルの最も単純な例を見て、単純なデータ分布からサンプルを生成するモデルのトレーニングを試みます。
謝辞
この記事をレビューしてくれたOlga Talanovaに感謝します。 英語版のコメント、編集、チェックをしてくれたSofya Vorotnikovaに感謝します。 Andrei Tarashkevichのレイアウトの助けに感謝します。