立ち下がり雪

1.はじめに

非常に負荷の高いポータルまたはAPIでは、たとえばユーザーを分類するために機械学習アルゴリズムの使用が必要になる場合があります。 このメモの一部として、いくつかの高性能線形モデルの実装プロセスと、基本的な理論原理の説明が示されます。

2.ペアワイズ線形関係

最も一般的に使用される単純なモデルから話を始めます。 明確な線形関係を持つメトリックのペアがあると仮定します。 データを視覚的に表示します。最初のメトリックの値は横座標に沿ったポイントの位置であり、2番目のメトリックの値は縦座標に沿ったポイントの位置です。 この図は、説明変数（予測変数、回帰変数、または独立変数とも呼ばれる）が増加すると、従属変数も増加することを示しています。 明確にするために、理論的な例をRに示します。

a <- c(1, 5, 5, 6, 4, 8, 9, 11, 15, 18, 22, 28, 29, 31, 31, 32) b <- c(1, 5, 6, 4, 5, 8, 9, 10, 17, 19, 22, 28, 28, 30, 30, 32) plot(a, b) abline(lm(b ~ a), col = "blue")
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

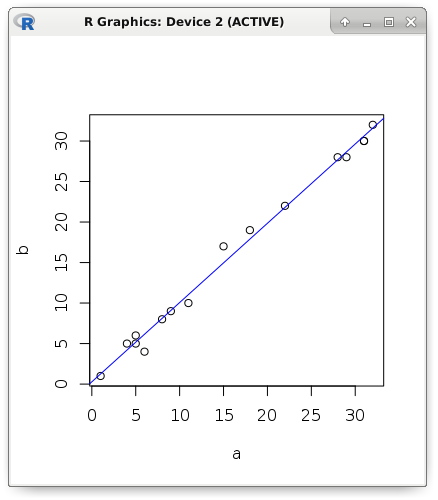
このようなアルゴリズムを記述する必要があります。このアルゴリズムは、線形依存性の存在の事実を明らかにし、その重大度を測定する必要があります。 正式に言えば、カールピアソンの線形相関係数を計算する必要があります。 理論的な基礎を思い出し、計算式をより詳細に扱うことを提案します。

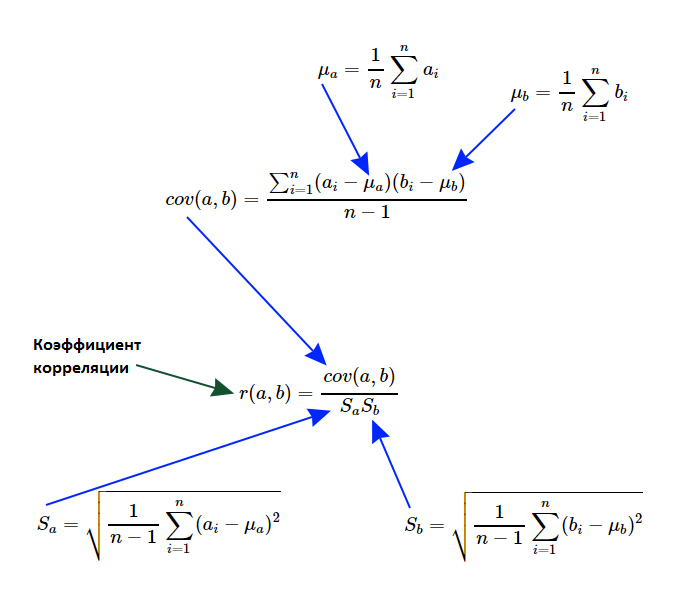
まず、このようなセットの特性に興味があります。これは、ランダム変数の分散と呼ばれます。 セットの各要素から平均値を引き、結果を2乗すると、新しいセットが得られます。その平均値は、一般母集団の確率変数の分散と呼ばれます。 理解できるように、元のセットのすべての要素が同じである場合、分散はゼロになり、要素が平均からより大きく逸脱するほど、分散は大きくなります。 それでも、負の数にすることはできません。

 var_a <- sum((a - mean(a)) ^ 2) / (length(a) - 1) c(var(a), var_a) # 127.2625 127.2625 c(sd(a), sqrt(var_a)) # 11.28107 11.28107
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

上記の例では、セットのパワーで割ったのではなく、それより1つ少ない値で割ったことに注意してください。 つまり、母集団ではなくサンプルの分散を計算しました。 また、平均値と要素の差が二乗されたため、分散から平方根を抽出して標準偏差を取得するのが理にかなっています。 関係を見つけるには、2番目のセットの標準偏差を知る必要があります。

 var_b <- sum((b - mean(b)) ^ 2) / (length(b) - 1) c(var_b, var(b)) # 122.7833 122.7833 c(sd(b), sqrt(var_b)) # 11.08076 11.08076
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、2つの量の線形依存性の測度を共分散として計算する必要があります。 式は分散に非常に似ており、さらに、セットが同一である場合、実際に確率変数の分散を取得します。 式は対称性を示しているため、引数の順序は任意です（セットを交換することができます）-AとBの共分散はBとAの共分散に等しい

 cov_ab <- sum((a - mean(a)) * (b - mean(b))) / (length(a) - 1) c(cov(a, b), cov_ab) # 124.525 124.525
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

実際、カールピアソンの線形相関係数は、単に共分散とセットの標準偏差の積の比です。 共分散とは異なり、解釈するのは非常に便利です。常に-1〜1の範囲にあります。ユニティに近いほど、線形相関が高くなります。 また、-1に近いことは負の相関を示します（言い換えると、1つの変数が大きいほど、他の変数は小さくなります）。 ゼロから大幅に逸脱していない場合、これは弱い依存関係を示しています。 はっきりと表された排出物のない線形関係についてのみ話していることを強調することは非常に重要です。さもなければ、この係数の使用は意味をなさないでしょう。

 cov_ab / (sqrt(var_a) * sqrt(var_b)) # 0.9961772 cor(a, b) # 0.9961772
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

線形相関係数は、依存関係が保持されるため、データを正規化または標準化した後に計算できます。 初期データの標準化と正規化の両方の前述の変更について考えてみましょう。 最初のケースでは、セットの各要素から平均値を減算し（この値の平均からの偏差の強さを取得）、それを標準偏差で除算しました。 その結果、平均値が0で分散が1の新しいセットが得られました。2番目のケースでは、各要素から最小値を減算し、変動範囲で除算しました（データは0〜1の範囲になります）。

 #  nm <- function(a) { (a - mean(a)) / sd(a) } #  snt <- function(a) { (a - min(a)) / (max(a) - min(a)) } cor(a, b) # 0.9961772 cor(nm(a), nm(b)) # 0.9961772 cor(snt(a), snt(b)) # 0.9961772
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ペアの線形依存性を観察して、その直線を近似します。 2番目のメトリックのみがわかっている場合、これにより、1つのメトリックの値が予測されます。 ペアワイズ線形依存性を正確に調査しているため、2つのパラメーターのみを計算する必要があります：定数（交差、オフセット、切片）と単一の予測子の係数、つまり 線の勾配（勾配）。 予測子係数を計算するには、予測子と従属変数の標準偏差を除算した結果を相関に乗算するだけで十分です。 交点はさらに簡単に見つけることができます。予測変数の平均値から、係数と従属変数の平均値の積の結果を引きます。

 slope <- cor(a, b) * (sd(b) / sd(a)) intercept <- mean(b) - (slope * mean(a)) c(intercept, slope) # 0.2803261 0.9784893
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

依存関係が機能的ではなく、確率的である場合、何らかのエラーが表示されます。 例を考えてみましょう。 予測変数のみがわかっている場合は、線形回帰を使用して従属変数の値を予測してみましょう。 赤で、厳密に線上にある予測値を表示し、黒で実際の値を表示します。

 y <- (0.2803261 + (0.9784893 * a)) plot(a, b) points(a, y, col = "red") abline(lm(b ~ a), col = "blue")
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

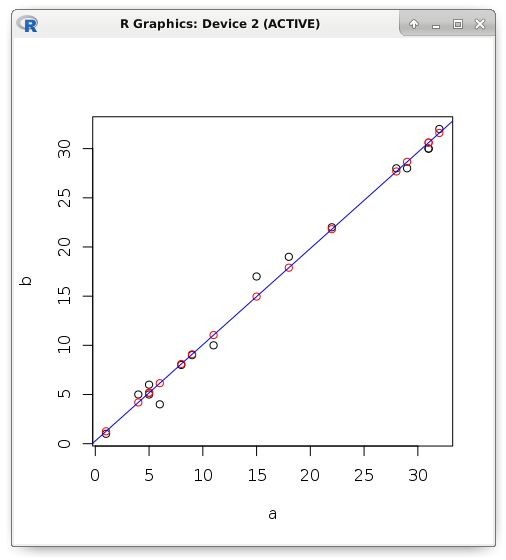
誤差は、実際の値と予測値の差です。 たとえば、プログラミング言語Rでは、説明的なエラー統計が「残差」セクションに表示されます。 堅牢な（耐干渉性）測定結果が表示されます。 並べ替えられたセットの中央（中央値）は、下位または上位の四分位数だけでなく、外れ値（干渉）に対して耐性があります。 平均値は、排出に耐性がないため、ここでは使用しません。 最大値と最小値が固有のレコードであると推測することは難しくありません（最も重大な間違い）。

 summary(lm(b ~ a)) # Residuals: # Min 1Q Median 3Q Max # -2.15126 -0.61350 -0.09749 0.50744 2.04233 # # Coefficients: # Estimate Std. Error t value Pr(>|t|) # (Intercept) 0.28033 0.44308 0.633 0.537 # a 0.97849 0.02293 42.669 3.17e-16 *** # --- # Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 #
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

さらに、前に計算した切片および予測係数が表示されます。 隣接する列は標準エラーです。 次に、係数がゼロであるという帰無仮説をテストするt統計を示します（係数からゼロを減算しても意味がないため、単純に係数を標準誤差で除算します）。 有意水準は、帰無仮説を棄却するのに十分な大きさです。 明確にするために、手動で取得したインジケーターを計算します。

 e <- (b - y) # Residuals: c(min(e), quantile(e, .25), median(e), quantile(e, .75), max(e)) # -2.15126190 -0.61349440 -0.09748515 0.50744140 2.04233440 # Std. Error (a) sqrt(sum(e ^ 2) / ((length(e) - 2) * sum((a - mean(a)) ^ 2))) # 0.02293208 # t value (a) 0.9784893 / 0.02293208 # 42.66902 # Pr(>|t|) (a) round((pt(42.66902, df = 14, lower.tail = FALSE) * 2), digits = 18) # 3.17e-16
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

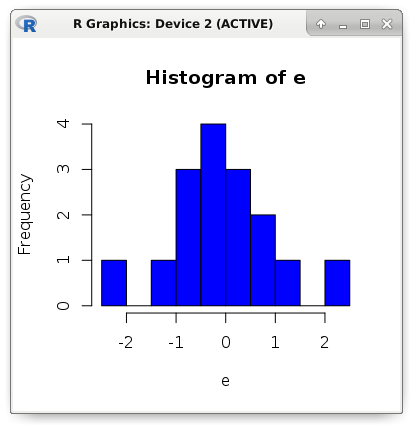
次のメトリックを使用して、モデルの精度を評価します：MSE、MAE、およびRMSE。 MSEという名前は、英語の平均平方誤差に由来しています。 これは平均二乗誤差です。 メトリックMAE（平均絶対誤差）は、誤差の平均絶対値です。 言い換えれば、最初のケースではエラーの平均二乗を取得し、2番目ではエラー係数の平均を取得します。 RMSE（二乗平均平方根誤差）メトリックは、単にMSEの平方根です。

 mae <- mean(abs(e)) mse <- mean(e ^ 2) rmse <- sqrt(mse) c(mae, mse, rmse) # 0.7131298 0.8783887 0.9372239 hist(e, breaks = 10, col = "blue")
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

3.既存のモデルを転送する

さらに実用的な側面に移りましょう。 単一の予測変数の値によって従属変数の値を検出する機能を追加する必要がある非常に負荷の高いAPIがあるとします。 実際、近似（回帰）の問題について話している。 線形関数の実装は、非常にコンパクトで高性能なコードによって区別されます。

APIはPHP7で作成されていると想定しています。 外部システムはモデルの原則について何も知らないことを思い出させてください。 すべての作業ロジックは1つのクラスにカプセル化されます。 入力データと戻り値の要件のみがわかっています。 戦略設計テンプレートが示唆するように、クライアントはインターフェースを実装する任意のクラスを使用します。 このインターフェイスでは、1つの引数（予測子）を取り、別のスカラー値（従属変数）を返す1つのメソッドの実装が必要です。

 <?php declare(strict_types = 1); interface IModel { /** * @param float $x * @return float */ public function predict(float $x): float; } class Example implements IModel { /** * @var float */ const SLOPE = 0.9784893; /** * @var float */ const INTERCEPT = 0.2803261; /** * @param float $x * @return float */ public function predict(float $x): float { return (self::INTERCEPT + (self::SLOPE * $x)); } } class Client { /** * @var IModel */ private $_model; /** * @param IModel $model */ public function setModel(IModel $model) { $this->_model = $model; } /** * @param float $x * @return float */ public function run(float $x): float { return $this->_model->predict($x); } } $client = new Client(); $client->setModel(new Example()); echo $client->run(17);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

比較のために、ペア線形関係の完全なコードを書くことができます。

 <?php declare(strict_types = 1); class Model { /** * @var float */ public $slope = 0.0; /** * @var float */ public $intercept = 0.0; /** * @param array $x * @param array $y */ public function fit(array $x, array $y) { $this->slope = Stat::cor($x, $y) * (Stat::sd($y) / Stat::sd($x)); $this->intercept = Stat::mean($y) - ($this->slope * Stat::mean($x)); } /** * @param float $x * @return float */ public function predict(float $x): float { return ($this->intercept + ($this->slope * $x)); } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

別のクラスに記述統計メソッドを実装しました。

 <?php declare(strict_types = 1); class Stat { /** * @param array $values * @return float */ public static function max(array $values): float { return max($values); } /** * @param array $values * @return float */ public static function min(array $values): float { return min($values); } /** * @param array $values * @return float */ public static function sum(array $values): float { return array_sum($values); } /** * @param array $values * @return float */ public static function mean(array $values): float { return self::sum($values) / count($values); } /** * @param array $values * @return float */ public static function variance(array $values): float { $mean = self::mean($values); $pow = array_map(function($v) use ($mean) { return pow($v - $mean, 2); }, $values); return self::sum($pow) / (count($pow) - 1); } /** * @param array $values * @return float */ public static function sd(array $values): float { return sqrt(self::variance($values)); } /** * @param array $a * @param array $b * @return float */ public static function cov(array $a, array $b): float { $meanA = self::mean($a); $meanB = self::mean($b); $diff = []; for($i = 0; $i < count($a); $i++) { $diff[] = ($a[$i] - $meanA) * ($b[$i] - $meanB); } return self::sum($diff) / (count($diff) - 1); } /** * @param array $a * @param array $b * @return float */ public static function cor(array $a, array $b): float { return self::cov($a, $b) / (self::sd($a) * self::sd($b)); } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

タスクを複雑にしましょう。 予測子の数は任意です。 これは直線ではなく、多次元空間の超平面です。 そして、問題の種類を近似から分類に変更します。 たとえば、ロジスティック回帰の助けを借りて、バイナリ分類の問題が解決されました。 たとえば、ユーザーを分類するために、非常に負荷の高いサービスでこの統計モデルを使用します。 この問題を解決するには、モデル学習アルゴリズム自体は必要ありませんが、分離超平面のパラメーターのみが必要です。

この状況では、モデルの原理は変わりません。 同様に、予測変数に対応する係数を乗算した結果を要約する必要があります。 次に、受信量にインターセプトが追加されます。 バイアスの代わりに、人工定数予測子が追加される場合があり、その場合、数式全体は、予測子とその係数の積（特徴ベクトルによる重みベクトルのスカラー積）の合計にのみ削減されます。

分類問題については、計算結果を所定のしきい値と単純に比較します。 値が大きい場合、最初のクラスが割り当てられます。それ以外の場合-ゼロ。 そのようなモデルの転送は同一になります。 このような線形モデルの2つの最も重要な利点は、コンパクトなコードと非常に高いパフォーマンスです。 これにより、文字通りオンザフライで、特徴のベクトルに従って観測クラスを識別できます。

 #   dataset <- read.csv('dataset.csv') #      pairs(dataset, col = factor(dataset$class)) #     model <- glm(formula = class ~ ., data = dataset, family = binomial) #    b <- model$coefficients #    ,    nc <- (b[1] + (dataset$alpha * b[2]) + (dataset$beta * b[3])) > 0 plot(dataset$alpha, dataset$beta, col = factor(nc))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

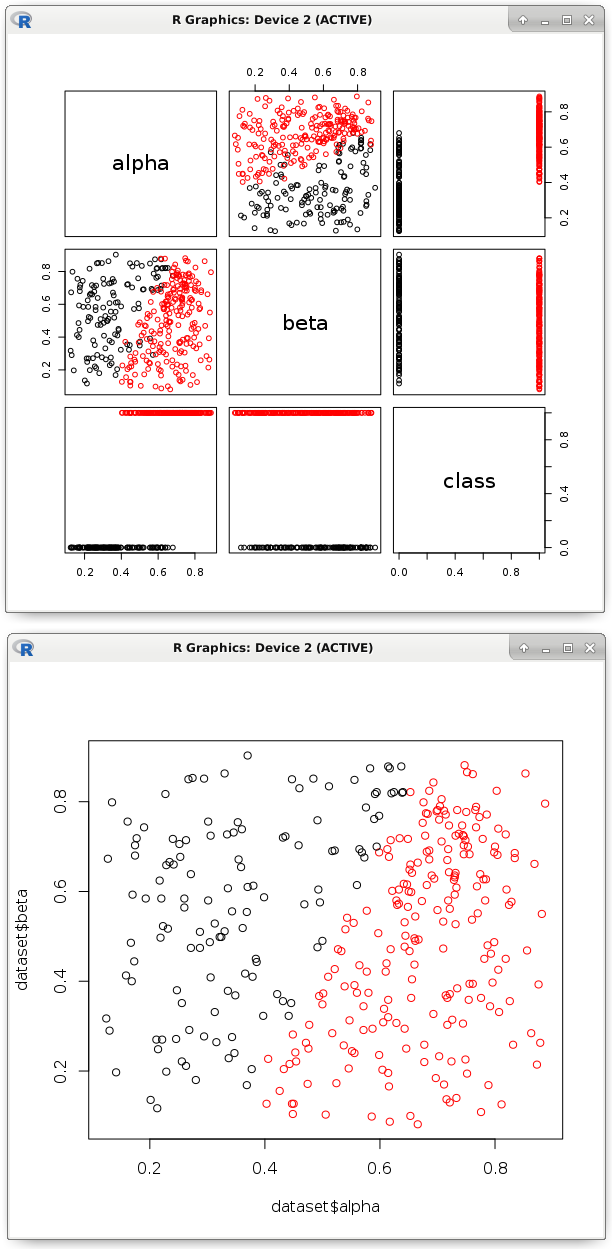
画像は、同様の線形関数がポイントを2つのクラスに分割したことを示しています。 実際、そのパラメーターは別のプログラミング言語のコードにエクスポートする必要があります。 これまで見てきたように、これは簡単なタスクです。 このプロセスは、自動化に非常に役立ちます。 主なことは、そのような超平面が正しく分類され、すべての予測変数が本当に必要であることを確認することです。

モデルをトレーニングし、その精度を確認するには、異なるデータセットを使用する必要があります。 多数の分類精度メトリックがありますが、その主なものは間違いなく検討します。 まず第一に、正確な答えの確率メトリックを思い出すことを提案します。 正解数をすべての回答数で割って計算されます。

 test <- factor(as.logical(dataset$class)) length(nc) # 345 table(test == nc) # FALSE TRUE # 17 328 328 / 345 # 0.9507246
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

しかし、クラスの1つの観測値の割合が1000分の1パーセントに過ぎない場合はどうでしょうか？ ここでは、定数を発行する分類器でさえ、驚くべき結果を示します。 混同マトリックスを表示することは理にかなっています。 バイナリ分類では、クラスラベルの予測結果は4つしかありません。 真のポジティブな結果は、ポジティブなクラスの正しい推測と呼ばれます（TRUEはTRUEと予測されます）。 真の負-負のクラスの真の推測（FALSEはFALSEと予測）。 偽陽性はFALSEがTRUEと予測され、偽陰性はTRUEがFALSEと予測されると仮定するのは論理的です。 特定の例を見てみましょう：

 table(nc, test) # test # nc FALSE TRUE # FALSE 120 8 # TRUE 9 208
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、「nc」は分類子の応答であり、「test」は真の答えです。 分類器の肯定的な応答のうち、実際に肯定的であった割合（精度、精度）を定義します。 完全性（リコール）と同様に、つまり このモデルによって特定された真陽性の割合。 これらの指標の意味は次のとおりです。彼が肯定的な答えをした場合、精度は分類器の信頼度を示します。 言い換えれば、これが確かにポジティブなクラスであると確信できる限りです。 しかし、完全性は、明らかにする能力の範囲を示しています。 特定された陽性の割合。 誤ってクラスをポジティブと呼ぶことを恐れている場合、精度がより重要です。 できるだけ多くのポジティブなものを見つける必要がある場合、完全性がより重要です。

 library(caret) precision <- posPredValue(factor(nc), test, positive = T) # 0.9585253 recall <- sensitivity(factor(nc), test, positive = T) # 0.962963 #  F1       f1 <- (2 * precision * recall) / (precision + recall) # 0.960739
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

正確さと完全性を手動で計算します。 混同マトリックスの値を置き換えるだけで十分です。

 # precision ( /  + ) 208 / (208 + 9) # 0.9585253 # recall ( /  + ) 208 / (208 + 8) # 0.962963
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

4.予測因子の重要性の評価

人々の複雑な心理学的研究が行われたと仮定します。 被験者の半分は神経症に苦しんでいますが、もう片方は順調です。 違いは何ですか？ または別の例：機器のパフォーマンスを測定しました-一部のデバイスはうまく機能しますが、他の問題があります。 これは何に影響しますか？ 従属変数と各予測変数の間の相関関係を探そうとする必要があると直感的に推測できます。 突然、燃料品質の測定基準は耐久性と強く相関していることが判明しました（燃料が優れているほど、デバイスの耐久性は高くなります）。 または、異なるクラスの観測値の予測子の平均値の違いを確認します。

ただし、データセットを視覚的に表示しようとします。 条件付きボーダーが表示され、その後、ドットの色が変わります。 アルファ予測子によると、0.5の領域で実行されます。 これは、分布のヒストグラムにも見られます（異なる色で表示）。 そして、ベータ予測によると、そのような明らかな違いは観察されていません。

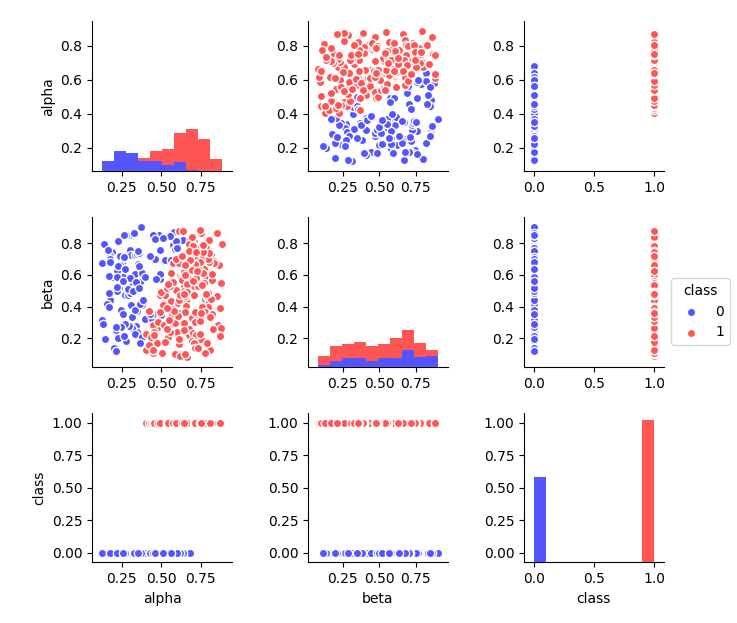
エラー（いくつかのポイントは誤って分類されることが判明しています）にもかかわらず、そのような基準は、ベータ予測子による可能な分離よりも効果的に問題を解決することは直感的に明らかです。 したがって、アルファの重要性は非常に高くなります。 分離後、目的のクラスのポイントを満たす可能性が大幅に増加します。 違いを明らかにするために、まず分離せずに確率を計算します。

 table(dataset$class) # 0 1 # 129 216 length(dataset$class) # 345 c(129 / 345, 216 / 345) # 0.373913 0.626087
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

確率がわかっているので、データの均一性のメトリックを計算します（同じクラスの代表のみである場合、Gini不純物インジケーターは0になります）。 ジニ不純物は、単位から減算される確率の二乗の合計として計算されます。

 # Gini impurity gini <- function(p) { (1 - sum(p ^ 2)) } gini(c(0.373913, 0.626087)) # 0.4682041
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

前述の条件に従ってすべてのポイントを分割します。 本質は、直感的なロジックに要約されます。最も有益な予測子による最も効果的な分離を選択する必要があります。

 node_1 <- subset(dataset, alpha > .5) table(node_1$class) # 0 1 # 25 197 length(node_1$class) # 222 #   gini(c(25/222, 197/222)) # 0.199862
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

取得した新しいサブセットごとに手順を再帰的に繰り返します。 これは、ある停止条件が発生するまで、たとえば、1つのクラスの観測のみが残るまで発生します。 これは、ノードが対応する検証条件（予測子と定数との比較）を持ち、終端ノード（葉）が同じクラスの観測値を持つ決定ツリーによって適切に記述されます。 ツリーはまず最も効果的な予測子を取得しようとするため、それらに沿った分離の条件はルートに近いノードに蓄積されます。 予測子による分離のレベル（深さ）がその重要性を反映していることがわかります。

 node_2 <- subset(node_1, beta < .29) table(node_2$class) # 1 # 34 length(node_2$class) # 34 #      gini(c(0/34, 34/34)) # 0
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

手作業で行うことは最も快適な作業ではないことに同意します。 これが、機械学習アルゴリズムが助けになる場所です。 残念ながら、決定木の集合はクラス間の違いを説明することはできません（むしろ、膨大な数の決定木を解釈することは困難です）が、予測子の重要性を計算できます。 これは、動作の原理が似ている近似問題にも適用され、分離基準のみが異なります。

このデータセットでは、予測子の1つが非常に重要であることは可能な限り明白でした。 クラスラベルとどのように相関するかを見てみましょう。

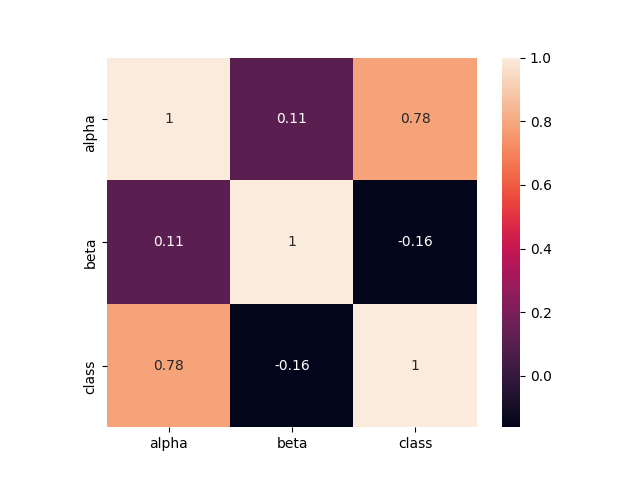
異なるクラスの平均値の違いも表示されます。 記述統計（PythonおよびRの例）を参照することをお勧めします。

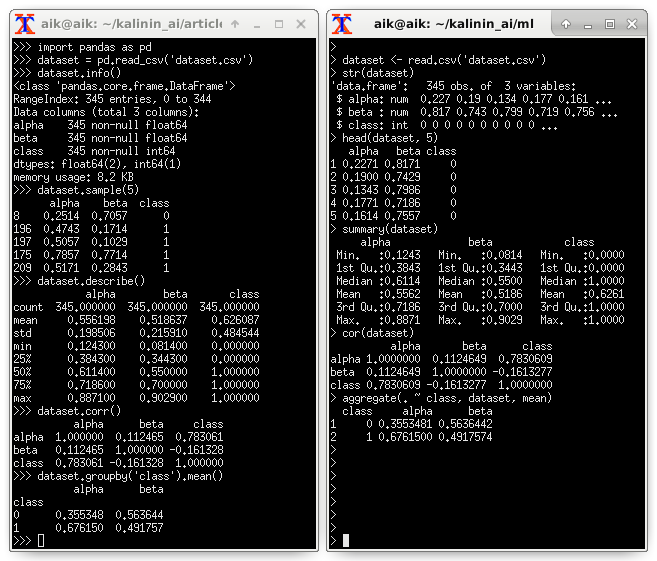
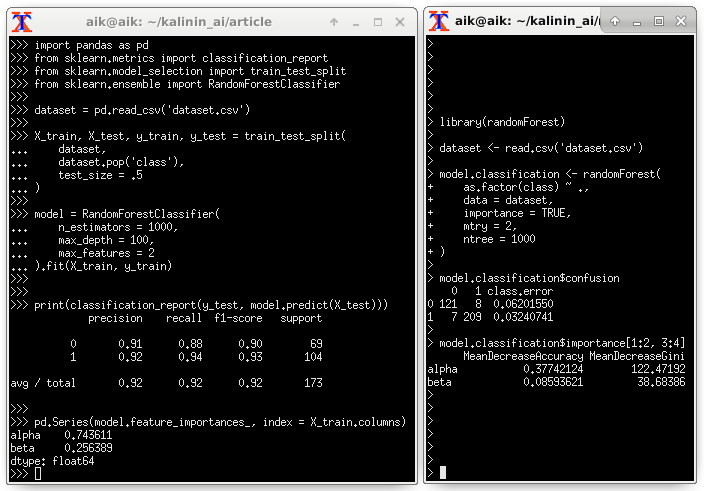
ランダムフォレストによる予測子の重要性の評価：

5.結論

このノートで説明されている線形モデルには、さまざまなプロジェクトに簡単に転送できる2つの主な利点があります。 1つ目は、コードのコンパクトさです（数学的操作のみ）。 第二に、非常に高いパフォーマンス。 ただし、すべてに欠陥があります。 残念ながら、ポイントを超平面で分離するのが困難な場合、または依存関係がそれによって近似されていない場合、効率は許容できないほど低いレベルになります。

6.アプリケーション

ソースコードスニペット（Python）を使用して、予測変数の重要性を特定しました。

 import pandas as pd dataset = pd.read_csv('dataset.csv') dataset.info() dataset.sample(5) dataset.describe() dataset.corr() dataset.groupby('class').mean()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 import seaborn as sns import matplotlib.pyplot as plt dataset.hist(bins = 20, figsize = (6, 6)) plt.show() sns.heatmap(dataset.corr(), square = True, annot = True) plt.show() sns.pairplot( data = dataset, hue = 'class', size = 2, palette = 'seismic' ) plt.show()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 import pandas as pd from sklearn.metrics import classification_report from sklearn.model_selection import train_test_split from sklearn.ensemble import RandomForestClassifier dataset = pd.read_csv('dataset.csv') X_train, X_test, y_train, y_test = train_test_split( dataset, dataset.pop('class'), test_size = .5 ) model = RandomForestClassifier( n_estimators = 1000, max_depth = 100, max_features = 2 ).fit(X_train, y_train) print(classification_report(y_test, model.predict(X_test))) pd.Series(model.feature_importances_, index = X_train.columns)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 from catboost import CatBoostClassifier from sklearn.model_selection import KFold from sklearn.metrics import confusion_matrix, f1_score kf = KFold(n_splits = 3, shuffle = True) dataset = pd.read_csv('dataset.csv') y = dataset.pop('class').values X = dataset.values columns = dataset.columns for train_index, test_index in kf.split(X): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model = CatBoostClassifier( calc_feature_importance = True ).fit(X_train, y_train) y_pred = model.predict(X_test) print(confusion_matrix(y_test, y_pred)) print(f1_score(y_test, y_pred)) print(list(zip(columns, model.feature_importances_)))