🤾🏻 👩 🖨️ バイナリマトリックスニューラルネットワーク 🧘🏻 ⌛️ 🍙

入力と出力がビットのセットである行列の形の人工ニューラルネットワーク。ニューロンはいくつかの変数のバイナリロジック関数を実装します。このようなネットワークはパーセプトロンタイプのネットワークとは大きく異なり、ネットワーク機能の完全な列挙のための有限数のオプション、したがって有限のトレーニング時間、および比較的単純なハードウェア実装などの利点を提供できます。

バイナリマトリックスニューラルネットワークを作成するための前提条件

人工ニューラルネットワークを作成しようとする試みは、その自然なプロトタイプの存在に基づいています。自然なニューラルネットワークで情報を送信および処理する方法は、生きているニューロン細胞の化学的および生物学的特性によって決まります。ただし、人工ニューラルネットワークモデルは、ニューロンの機能と自然な脳の構造の両方を完全にコピーする必要はありません。これは、情報入力を出力に変換する機能のみを実装しているためです。したがって、人工ニューラルネットワークの機能の実装は、その自然の対応と大幅に異なる場合があります。自然の脳の構造を直接コピーしようとすると、必然的に次の問題が発生しますが、解決しないと克服できない場合があります。ご存知のように、哺乳類の脳では、ニューロンの出力を他のいくつかのニューロンの入力に接続できます。

どのニューロンの入力を他のニューロンの出力と接続する必要があるかを調べる方法は？ネットワークがその機能を果たすために、ネットワーク内の特定の各ニューロンにいくつのニューロンを関連付ける必要がありますか？

これらの質問に対する答えはまだありません。また、実際の脳内のニューロンの数は数十億であるため、ブルートフォースによってニューロンを互いに接続すると、そのようなネットワークの学習時間がほぼ無限になります。

パーセプトロンタイプの人工ニューラルネットワークでは、隣接する層のすべてのニューロンが互いに接続されています。そして、コミュニケーションの「強さ」は、係数の値によって決まります。 all-with-all接続は、ブルートフォースを使用したニューロン接続の問題の解決策です。この場合、ニューラルネットワークは、たとえば数週間など、許容できるトレーニング時間の間、中間層に比較的少数のニューロンのみを含むことができます[2]。

たとえば、画像を分類するために、ニューラルネットワークが結果の生成を開始する前に、トレーニング段階、つまり調整段階を実行する必要があります。トレーニング段階で、相互作用の構成とネットワークニューロンの一般的な機能が決定されます。実際、ニューラルネットワークをトレーニングするとは、変換関数を選択して、指定された入力で指定されたレベルのエラーで正しい出力を提供することを意味します。次に、トレーニング後、ネットワーク入力に任意のデータを与えます。ニューラルネットワークの機能が十分に正確に選択され、ネットワークが他の入力データを正しく分類できるようになります。一般的なパーセプトロンタイプのネットワークでは、ネットワーク構造は最初に固定されており、たとえば[2]を参照してください。中間層のニューラルリンケージ係数を選択することで関数が見つかります。マトリックスの説明に進む前に、隣接する層のすべてのニューロンの同時接続は、ニューロン関数が前の層のニューロンの出力と結合係数の線形結合であるという事実を利用して、ニューロンのペアの連続した接続に分解できることに注意してください。つまり、少なくともパーセプトロンタイプのネットワークの場合、各ニューロンは、他の2つのニューロンのみからデータを受信するものとして表すことができます。

いくつかの並列接続を隣接ニューロンのみの結合のペアまたはトリプルのシーケンスに分解する原理は、以下に説明するマトリックスの基礎です。他のすべてをニューロンに接続することでネットワークをトレーニングする必要はまったくないという制限が受け入れられます。自分自身を隣接するニューロンのみに制限し、ネットワーク学習機能のエラーを順次減らすだけで十分です。このバージョンのニューラルネットワークは、著者の以前の研究に基づいています[1]。

マトリックスとニューロンの構造

ニューラルネットワークの次のマトリックス構造により、ニューロンの接続の問題を解決し、ニューラルネットワークの機能を検索する際の組み合わせの数を制限できます。このネットワークにより、理論的には、ネットワーク関数がいくつかの変数の離散ベクトル関数であるという事実により、入力/出力のトレーニングセットでエラーがゼロのニューラルネットワークの関数を見つけることができます。

図1は、バイナリマトリックスの例を示しています。この行列の入力と出力は、バイナリ4コンポーネントベクトルです。入力は下から供給され、上から出力値を取得します。行列の各セルは、いくつかの変数fのバイナリ関数を持つニューロンです。各ニューロンには水平および垂直の隔壁があり、隣接するニューロンから分離し、データの流れを決定します。各ニューロンの左側に表示されるニューロンの垂直中隔には、閉じた（暗いバー）、右側に開いた（右側の緑の矢印）、左側に開いた（左側の黄色の矢印）の3つの位置があります。

ニューロンの下に描かれた水平中隔には、閉じた「停止」（暗いバー）または開いた（緑の矢印）の2つの位置があります。したがって、マトリックス内のデータフローは、下から上、左/右になります。データの境界放電の割り当てを回避するために、各行の最初と最後のニューロンは論理的にループします。つまり、たとえば、行の最初のニューロンの左矢印は、2行目のニューロンの図1に示すように、同じ行の最後のニューロンの入力です。

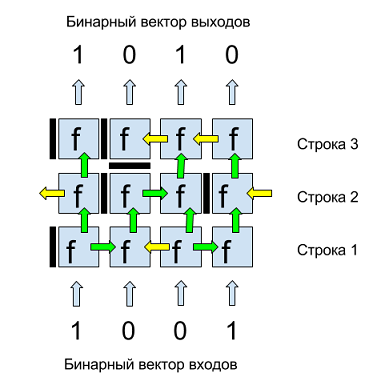
図 1. 3行と4つのバイナリ入力/出力のバイナリマトリックスの例。

マトリックスの構造は、段階的な行ごとの構築の規則に従います。この一連のニューロンが問題を解決しない場合、次のものが追加され、目的関数が達成されるまで続きます。

トレーニングの前に、マトリックスは最初の1行で構成されます。マトリックストレーニングでは、行を順番に追加します。現在の行で1つ以上のセプタム構成を見つけた後、新しい行が追加されます。また、マトリックスのトレーニングセットのエラー値が最小で、前の行の学習エラーの値よりも小さいニューロンの内部パラメーターも検索されます。

ニューロンは、データの変換、信号の送信または停止の機能を実行します。ニューロンfの関数は、パーティションと内部定数の現在の構成に応じて、次の必須要件を満たす必要があります。

1.データを変更せずに転送できる。

2.入力データなしで定数（0または1）を送信できる。

3.隣接するニューロンからの入力データの適用順序に依存してはなりません。つまり、ニューロンは、受け取ったすべての入力から結果として得られた値を、そのままで与えます。

このような関数fのオプションの1つは、2を法とする加算または排他的ORまたはXORです。これは、プログラミング言語でよく示されています。

変更なしの転送とは、ニューロンが実際に存在しないことを意味し、データを変更せずにマトリックスレベルを送信するという観点からのみ必要です。

ニューロンは、信号処理と送信に加えて、ニューロンによって実装される機能に応じて、メモリ機能とその使用または非使用も備えています。

ニューロンとその隣接ニューロンのパーティションの位置（値）に応じて、各ニューロンは0から3つの入力（下、右、左）と常に1つの出力（上）を持つことができますが、次の行のニューロンに接続されない場合があります、上部ニューロンの水平中隔の位置が「停止」するため。

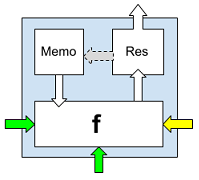
ニューロン回路

図 2.二項関数f 、メモセル、およびResフィールドを持つニューロン。

各ニューロンは同じバイナリ関数fを実行しますが、これはニューロンのセプタムの構成に応じて入力値の数のみが異なり、前の行のニューロンと2つの横方向に隣接するニューロンからの入力データと、バイナリ内部定数Memoからの入力データを許可します。

ニューロンは入力データを受け取り、入力とメモフィールドに基づいてニューロンfのバイナリ関数を実行し、結果をResフィールドに入れます。メモフィールドを使用するオプションは異なる場合があります。マトリックス全体の出力がネットワークの入力のみに依存する場合、Memoフィールドはニューロンの壁の値とともにネットワーク構成の一部になります。ネットワークを以前の値に基づいてトレーニングする必要がある場合、つまり、たとえば人工生命の実装のためにメモリを所有する必要がある場合、メモフィールドは、図5に示すように、新しく計算されたRes値を取ることができます 2点線矢印。

ニューロン関数fは、すべての入力パラメーターに順次適用されるバイナリXOR演算であると仮定します。 3つの必要な要件を満たしていることを確認します。

1.変更なしのデータ伝送は、図に示されているオプションによって提供されます。 3.ここで、Memo = 0、「up」値の水平の下部パーティション、「stop」値の左右のパーティション。

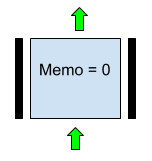
図 3. f = XORの場合に変更することなく、前の行からの入力の転送を実装するニューロンパラメーターのバリアント。

2.定数の転送は、水平および垂直の「停止」パーティションの値によって提供され、メモ値は送信された定数の値です。

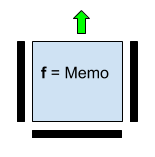
図 4.独立した2進定数メモを転送する機能を持つニューロン。 下、左、右の入力値は使用されません。

3.ニューロンの入力値を処理するシーケンスからのニューロン関数の値の独立性の要件は、XOR結合により保証されます。

文字列関数の完全な列挙の組み合わせの数

行列関数のシーケンシャルな行ごとの構築により、すべての行列ニューロンのバイナリ関数の組み合わせの完全な列挙を行ニューロン関数の組み合わせの完全な列挙に置き換えることにより、学習プロセスを効果的に最適化できます。ネットワークトレーニングの重要なポイントの1つは、1行のニューロンの機能の完全な列挙の組み合わせの数です。

上記のニューロンバリアントの場合、ニューロンの機能の列挙には以下が関与します。

1.停止と上昇の2つの位置を持つ水平パーティション。

2.ストップ、左、右の3つの位置を持つニューロンの垂直中隔。

3.値が0および1のバイナリフィールドメモ。

これらのパラメーターの組み合わせに基づいてニューロン関数のバリアントの数を計算するには、これらのパラメーターごとに値のバリアントの数を乗算します。

Q_{n} = 2 t i m e s 2 t i m e s 3 = 12

$Q_n = 2 \ times2 \ times3 = 12$ 。したがって、各ニューロンは、入力に渡されたパラメーターの数に応じて、バイナリ関数の12のオプションのいずれかを持つことができます。 8個のニューロンの行列の1行の関数の完全な列挙のオプションの数を計算します。したがって、1バイトサイズのデータを処理できます。

Q_{s} = 12^{8} = 429 \： 981 \： 696

$Q_s = 12 ^ 8 = 429 \：981 \：696$ 。

現代のパーソナルコンピュータの場合、これは非常に多くの計算ではありません。メモフィールドがない場合など、オプションの少ないニューロン関数を選択すると、組み合わせの数が大幅に減少して

6^{8} = 1 \： 679 \： 616

$6 ^ 8 = 1 \：679 \：616$ 。ニューロン機能のこのような大幅に簡素化されたバージョンでさえ、最適化中の学習エラーの減少を示しています。 C＃言語のニューラル関数のさまざまなバリアントを使用したソフトウェアテストでは、著者は1秒あたり20万から60万バリアントの範囲の列挙速度を得ることができました。これにより、約3秒で行列行関数のオプションが完全に列挙されます。ただし、これは、たとえば、8x8マトリックスが24秒でトレーニングされることを意味するものではありません。実際には、同じ現在の学習エラー（メトリック）の最小値を与える文字列関数のいくつかの可能なバージョンがあります。これらの数十、数百、または数千の組み合わせのどれがマトリックス全体の学習でゼロエラーになるかはわかりませんが、最悪の場合、それらのそれぞれをチェックする必要があり、最適化検索ツリーの構築につながります。

問題は自然に発生し、ニューロンfのどの二項関数が行列を学習するのに最適であるかということです。明らかに、パーティションとメモ型フィールドのパラメーターの特定のセット内の行列の行に対して機能的完全性[3]の機能を持つ関数が理想的です。この場合、完全ではないにしても、学習エラーがゼロの行列を見つける保証が大きくなります。ただし、そのようなニューロン機能を見つける問題は、まだ研究する必要があります。

最適化ツリーの構築またはゼロマトリックス学習エラーの検索

マトリックス学習エラー関数は、メトリックと呼ばれます。メトリック値は、トレーニングデータで予想される値からのマトリックス出力の偏差の程度を示します。

メトリックの例。行列の入力と出力が4ビットの数値であると仮定します。そして、入力数を乗算するように行列を訓練したい

2

$2$ 。 3つの入力値がトレーニングに使用されるとしましょう

\ {1、2、3 \}

$\ {1、2、3 \}$ 、数字がある理想的な

R_1、R_2、R_3：\ {2、4、6 \}

$R_1、R_2、R_3：\ {2、4、6 \}$ 。

その場合、マトリックスの学習入力は4ビット値になります。

\ {0001、0010、0011 \}

$\ {0001、0010、0011 \}$ 、および出力

\ {0010、0100、0110 \}

$\ {0010、0100、0110 \}$ 、入力および出力文字列ニューロンごとにそれぞれ1ビット。

マトリックスの学習プロセスは、ニューロンのセプタムの位置と文字列のニューロン内のメモフィールドの値を順番に並べることで構成され、これらが一緒になって検索パラメーターとして機能します。これらのパラメーターのいずれかを変更するたびに、たとえば、ニューロンの1つの水平中隔の位置を「停止」位置から「アップ」位置に変更するか、Memoフィールドの値を1から0に変更した後、パーティションとフィールドの現在の組み合わせを取得し、メトリック値を計算します。

パーティションとメモ型フィールドの特定の組み合わせでメトリック値を取得するには、トレーニング入力の値をマトリックスに置き換えて出力を取得します。

たとえば、パーティションとフィールドの組み合わせで、マトリックスの出力値を取得しました

\ {0010、0001、1000 \}

$\ {0010、0001、1000 \}$ 。それらを10進数に変換します

r_1、r_2、r_3：\ {2、1、8 \}

$r_1、r_2、r_3：\ {2、1、8 \}$ 。

マトリックスの現在の出力のメトリック値を取得します。

M = s u m l i m i t s_{i = 1}^{3} | R_{i} - r_{i} | = | 2 - 2 | + | 4 - 1 | + | 6 - 8 | = 5

$M = \ sum \ limits_ {i = 1} ^ 3 {| R_i-r_i |} = | 2-2 | + | 4-1 | + | 6-8 | = 5$

この場合、学習エラーは5であり、タスクは、メトリック値が小さいマトリックスの現在の最上行でこのようなニューロンの構成を見つけることです。

5

$5$ 。

メトリックゼロを見つけるためのオプションの1つを検討します。このオプションでは、トレーニングデータの最小メトリック値を与えるパーティションとメモフィールドの構成で、行列の各新しい行が前の行に追加されます。

行列最適化ツリーを構築するための一般的なアルゴリズム。

1.     ,  max(Int32).  ,          ""    Memo. 2. :                 . a.        ,     ,         ,    . b.     ,           . c.      ,   ,        . d.     ,       (  )   . 3.                 ,             .

このアルゴリズムの詳細は、メモリの節約と作業の高速化の両方の点で異なる場合があります。たとえば、現在のメトリック値の減少に応じて、マトリックスニューロンを分割する構成機能によるリストの並べ替えや、以前のブランチリストの破棄などです。

おわりに

実際の実験では、ほとんどの場合、マトリックス学習アルゴリズムが収束することが示されています。たとえば、XORニューロン関数を使用したテストの1つでは、8ビット幅のマトリックスが学習エラーなしで1〜6の2つの数値を乗算することを学習しました。入力に7を代入すると、出力で14になります。これは、マトリックスが1つ先の動きを推定することを学習したことを意味しますが、すでに8番でマトリックスの結果が間違っています。すべてのトレーニングは、自宅のパソコンで数分かかりました。ただし、より複雑なトレーニングサンプルでの実験には、異なる計算能力が必要です。

データをボトムアップで送信することに加えて、マトリックスの現在の構成の一部のニューロンが結果を前の行に送信する場合、逆方向のフローも考慮することができます。一方で、そのような構成は、循環データを含む異常なマトリックス関数を与えることができますが、一方で、ソリューションオプションを列挙するときにもう1つの構成パラメーターを追加するため、マトリックスの学習時間を増やします。

平面ニューロンから、3次元ニューロンに移動できます。それらを正方形の要素としてではなく、それぞれの面がデータを送受信する立方体として考えると、（これまでのところ理論的には）完全に実体のある3次元人工脳を得ることができます。

参照資料

1. AV Kazantsev、バイナリニューラルネットワークを使用した視覚的データ処理およびアクション制御-IEEE第8回国際ワークショップ（WIAMIS '07）マルチメディアインタラクティブサービスの画像分析、2007年。

2. Natalya Efremova、ニューラルネットワーク：実用化（habrahabr.ru）

3. ブール関数の機能的完全性（Wikipedia）

バイナリマトリックスニューラルネットワーク