二次算術プログラム：ぼろから富へ（翻訳）

zk-SNARKsテクノロジーに関する一連の記事を続けて、Vitalik Buterinによる非常に興味深い記事「 二次算術プログラム：ゼロからヒーローまで 」を研究しています。

前の記事： 例付きzk-SNARKの概要（翻訳）

最近、zk-SNARKs技術への関心が非常に高まっており、人々はかなり聞こえない複雑さのために、多くの人が「月の数学」と呼ぶようになったものの謎を解こうとしています。 zk-SNARKsは、特にそれを機能させるために組み合わせる必要のある多数のコンポーネントのために、理解するのが非常に難しいですが、テクノロジーを分解すると、理解しやすくなります...

この出版物の目的は、zk-SNARKテクノロジーを完全に紹介することではありません。 また、最初に、zk-SNARKが何であり、何をするかを知っていること、そして次に、多項式のようなことについて推論できるほど十分に数学を知っていると仮定されます（ステートメントP(x) + Q(x) = (P + Q)(x)



。ここで、 P



とQ



は多項式であり、自然で明白なように見えますが、レベルは十分です）。 むしろ、この出版物はテクノロジーの背後にあるメカニズムを明らかにし、zrankの研究者Eran Tromerが示した変換の前半を可能な限り説明しようとしています。

ここでの変換は、2つのコンポーネントに分けることができます。 まず、zk-SNARKは計算上の問題に直接適用できません。 まず、タスクを解決する問題の正しい「フォーム」に変換する必要があります。 フォームは「2次算術プログラム」（QAP）と呼ばれ、関数コードをそのようなフォームに変換することはそれ自体非常に重要なタスクです。 関数コードをQAPに変換することに加えて、変換する関数の入力引数がある場合に実行される別のアクションがあります。 適切なソリューションを作成する必要があります（QAPの「証拠」と呼ばれることもあります）。 このエビデンスの実際の「ゼロ開示エビデンス」を作成する別のやや複雑なメカニズムと、渡されたエビデンスを検証する別のプロセスもありますが、これは本書の範囲外の別の会話です。 （プロセスの一般的なスキームを理解するには、 最初の記事を参照してください 。注。翻訳者）。

簡単な例を取り上げます。3次方程式の解を知っていることを証明する必要があります。

$$

$$x ^ 3 + x + 5 = 35$$

（ヒント：回答3）。 このタスクは非常に単純なので、結果のQAPはあなたを怖がらせるほど大きくありません。 ただし、実行中のすべての数学を見ることができるように、コードは十分に重要です。



次のように機能を説明します。

 def qeval(x): y = x**3 return x + y + 5
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで使用される単純な専用プログラミング言語は、基本的な算術演算（ +, -, *, /



）、限定指数（ x**7



ではなくx**y



）、および変数割り当てをサポートします。関数内で計算を実行する理論（計算ステップの数は制限されており、サイクルの使用は許可されていません）。 モジュロ除算（ %



）および比較演算子（ <,>, ≤, ≥



）はサポートされていないことに注意してください。モジュロ除算または比較を完成した巡回グループ演算で直接実行する効果的な方法がないためです（これには感謝しますこれらの操作のいずれかを実装する方法があれば、楕円曲線の暗号化は、「バイナリ検索」や「中国剰余定理」と言うよりも速くハッキングされます。

ビット分解を使用して、モジュロ除算と比較に言語を拡張できます。次に例を示します。

$$

$$13 = 2 ^ 3 + 2 ^ 2 + 1$$

補助パラメータとして、これらの展開の正確性をチェックし、バイナリ演算で数学を実行します。 有限体演算では、等値チェック（==）も実行可能であり、さらに簡単です。しかし、これらのことは今は扱いません。 条件式をサポートするように言語を拡張できます（たとえば、 if x < 5: y = 7; else: y = 9



）。これらを算術形式y = 7 * (x < 5) + 9 * (x >= 5);



変換することにより、 y = 7 * (x < 5) + 9 * (x >= 5);



ただし、条件式の両方の分岐を満たす必要があり、ネストされた条件が多数ある場合は、オーバーヘッドコストが増加することに注意してください。



それでは、QAPへの変換プロセスを段階的に完了しましょう。 自分でコードを作成したい場合は、ここでコンパイラを実装しました （教育目的のみで、実際のzk-SNARKのQAPを作成する準備はまだできていません！）。

単純化

最初のステップは「単純化」手順です。 その中で、任意の数の複雑な演算子と式を含むことができるソースコードを、2つの形式を持つ一連の演算子に変換します。

x = y



（ y



は変数または数値の場合があります）および

x = y (op) z



（ op



は+, -, *, /



できますy



およびz



は変数、数値、または部分式を使用できます）。

これらの各演算子は、回路内の論理的な遷移（状態を変更する「論理ゲート」を意味します。翻訳者のメモ）として想像できます。 上記のコードの単純化プロセスの結果は次のとおりです。

 sym_1 = x * x y = sym_1 * x sym_2 = y + x ~out = sym_2 + 5
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ソースコードと上記のコードを見ると、それらが同等であることが簡単にわかります。

R1CSへの移行

現在、これを「ランク1制限システム」（R1CS）と呼ばれるものに変換しています。 R1CSは3つのベクトル（a、b、c）のグループのシーケンスであり、解R1CSはベクトルs



。ここで、 s



は式sa * sb - sc = 0



満たさなければなりません.



「ポイントを取る」 （行ベクトルと列ベクトルの乗算。トランスレータに注意）を表します。 簡単に言えば、 a



とs



を「合成」し、同じ位置でベクトルの値を乗算し、これらの積の合計をとってから、 b



とs



について同じことを行い、次にc



とs



について同じことを行いc



、最後に3番目の結果は最初の2つの結果の積に等しくなります。 R1CSソリューションの例：

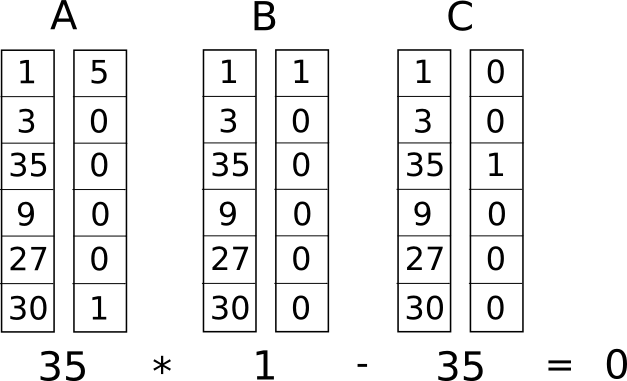
しかし、プログラムに1つだけの制限を設ける代わりに、多くの制限を導入します：各論理遷移に1つ。 実行される操作（+、-、*、または/）、および引数が変数か数値かによって、論理遷移を（a、b、c）トリプルに変換する標準的な方法があります。 各ベクトルの長さは、システム内の変数の総数に等しく、これには、値~one



ダミー変数~one



、入力パラメーター、結果を表すダミー変数sym1



、およびすべての中間変数（ sym1



およびsym2



参照）が含まれます。 原則として、ベクトルは非常に「放電」され、特定の論理遷移の影響を受ける変数に対応する値が入力されます。

使用する変数のリストを示しましょう。

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

解ベクトルは、これらすべての変数に同様の順序で値を割り当てることで構成されます。

ここで、最初の遷移の（a、b、c）トリプルを見つけます。

 a = [0, 1, 0, 0, 0, 0] b = [0, 1, 0, 0, 0, 0] c = [0, 0, 0, 1, 0, 0]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

2番目の位置の解ベクトルの値が3で、4番目の位置の解ベクトルが9の場合、解ベクトルの残りの値に関係なく、ベクトルの検証が3*3 = 9



削減され、解が正しいことを確認するのは簡単です。 解ベクトルの値が2番目の位置で-3、4番目の位置で9である場合、チェックも成功します。 同じことが、2番目の位置の値7と4番目の位置の49にも当てはまります。 この最初のテストの目的は、最初の遷移のみの入力と出力に一貫性があることを確認することです。

2番目のジャンプに移りましょう。

 a = [0, 0, 0, 1, 0, 0] b = [0, 1, 0, 0, 0, 0] c = [0, 0, 0, 0, 1, 0]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最初のチェックと同様に、ここではsym_1 * x = y



をチェックしsym_1 * x = y

3番目の移行：

 a = [0, 1, 0, 0, 1, 0] b = [1, 0, 0, 0, 0, 0] c = [0, 0, 0, 0, 0, 1]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここでパターンはわずかに異なります。解ベクトルの最初の要素に2番目の要素、次に5番目の要素を乗算し、2つの結果を加算して合計が6番目の要素と等しいかどうかを確認します。 解ベクトルの最初の要素は常に1に等しいため、これは単なる加算テストであり、出力が2つの入力の合計に等しいことを確認します。

最後に、4番目の移行：

 a = [5, 0, 0, 0, 0, 1] b = [1, 0, 0, 0, 0, 0] c = [0, 0, 1, 0, 0, 0]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここでは、最後のテスト~out = sym_2 + 5



を再現します。 チェックは、ソリューションベクトルの6番目の要素を取得し、最初の要素に5を加算し（最初の要素は1なので、実際には5を追加することを意味します）、出力変数を格納する3番目の要素と相関させます。

したがって、R1CSには4つの制限があります。 証拠は、入力、出力、内部変数を含むすべての変数の値です。

 [1, 3, 35, 9, 27, 30]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

入力変数x = 3の割り当てから始めて、上記の簡略化されたコードを「実行」するだけで、自分で計算できます。すべての中間変数の値を入力し、計算中に変更します。

ここで、ケースの完全なR1CSを提供します。

 A [0, 1, 0, 0, 0, 0] [0, 0, 0, 1, 0, 0] [0, 1, 0, 0, 1, 0] [5, 0, 0, 0, 0, 1] B [0, 1, 0, 0, 0, 0] [0, 1, 0, 0, 0, 0] [1, 0, 0, 0, 0, 0] [1, 0, 0, 0, 0, 0] C [0, 0, 0, 1, 0, 0] [0, 0, 0, 0, 1, 0] [0, 0, 0, 0, 0, 1] [0, 0, 1, 0, 0, 0]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

R1CS-QAP

次のステップは、このR1CSを同じロジックを実装するQAP形式に変換しますが、「ポイントを取る」代わりに多項式が使用されます。 これを次のように行います。長さ6の3つのベクトルの4つのグループから次数3の3つの多項式の6つのグループに移動します。多項式の各x



座標は制限の1つに対応します。 つまり、x = 1で多項式の値を計算すると、最初のベクトルのセットを取得し、x = 2から多項式を計算すると、2番目のベクトルのセットなどを取得します。

たとえば、ラグランジュ補間多項式を使用してこの変換を行うことができます。 ラグランジュ補間が解決する問題はこれです：点のセット（つまり(x, y)



座標ペア）がある場合、これらの点でラグランジュ補間を行うと、これらすべての点を通過する多項式が得られます。 これを行うには、次のようにタスクを分割しますx



各値に対して、指定されたポイント(x, y)



対応するy



値を返し、他のすべての場合に0を返す多項式を作成します。 そして、最終結果を得るために、すべての多項式を追加します。

例を挙げます。 （1、3）、（2、2）および（3、4）を通過する多項式が必要だとします。 （1、3）、（2、0）および（3、0）を通過する多項式を作成することから始めます。 判明したように、x = 1でのみ値を取り、他の場合はゼロに等しい多項式を作成することは非常に簡単です。

 (x - 2) * (x - 3)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

チャートでは、次のようになります。

ここで、「ズーム」するだけで、x = 1の高さが必要になります。

 (x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これにより以下が得られます。

$$

$$1.5 * x ^ 2-7.5 * x + 9$$

次に、他の2つの点で同じことを行い、他の2つの類似した多項式を取得します。ただし、x = 1ではなくx = 2およびx = 3で値を取得します。

3つすべての多項式をまとめて取得します。

$$

$$1.5 * x ^ 2-5.5 * x + 7$$

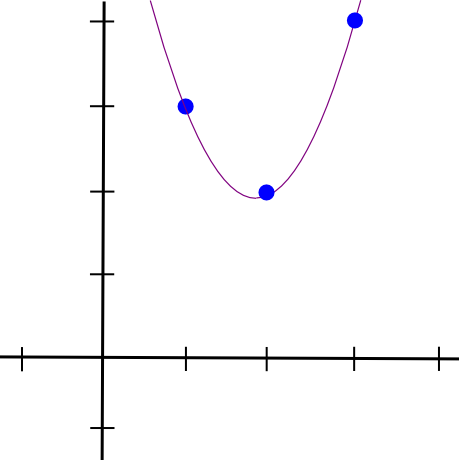
これがまさに私たちが必要とするものです。 上記のアルゴリズムの時間の複雑さはO (n^3)



であり、n個の点があり、各点は多項式を乗算するためにO (n^2)



時間を必要とします。 ビットを最適化することにより、複雑さをO (n^2)



減らすことができます。 また、高速フーリエ変換アルゴリズムなどを使用すると、複雑さを軽減できます。これにより、zk-SNARKが大幅に最適化されます。 実際には、実際の関数には何千もの遷移が含まれることがあります。

次に、R1CSをラグランジュ補間多項式に変換しましょう。 各ベクトルa



から最初の位置の値を取得し、ラグランジュ補間を適用して多項式を取得します（ポイントi



多項式の値を計算a



と、最初の位置のi番目のベクトルa



値が得られます）。 次に、各ベクトルb



およびc



最初の位置の値に対してプロセスを繰り返し、その後、後続の位置に対してこのプロセスを繰り返します。 便宜上、すぐに結果を表示します。

  A [-5.0, 9.166, -5.0, 0.833] [8.0, -11.333, 5.0, -0.666] [0.0, 0.0, 0.0, 0.0] [-6.0, 9.5, -4.0, 0.5] [4.0, -7.0, 3.5, -0.5] [-1.0, 1.833, -1.0, 0.166]  B [3.0, -5.166, 2.5, -0.333] [-2.0, 5.166, -2.5, 0.333] [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0]  C [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] [-1.0, 1.833, -1.0, 0.166] [4.0, -4.333, 1.5, -0.166] [-6.0, 9.5, -4.0, 0.5] [4.0, -7.0, 3.5, -0.5]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

係数は次数の昇順で並べ替えられるため、最初の多項式は0.833 x ^ 3-5 x ^ 2 + 9.166 * x-5.である必要があります。この多項式のセット（および多項式Z、後で説明する意味）はQAPインスタンスのパラメーターです。 これまで、zk-SNARKの確認に使用するのと同じ機能に対して、必要なアクションはすべて1回だけ実行されることに注意してください。 QAPパラメータが生成されると、再利用できます。

x = 1のこれらすべての多項式を計算してみましょう。x= 1の多項式を推定することは、すべての係数を加算することを意味します（任意のkに対して1 ^ k = 1であるため）。これは難しい作業ではありません。 取得します：

  A  x=1 0 1 0 0 0 0  B  x=1 0 1 0 0 0 0  C  x=1 0 0 0 1 0 0
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、上記で作成した最初の論理遷移に対して、同じ3つのベクトルのセットを取得しました。

QAP検証

では、これらすべてのクレイジーな変換の意味を見てみましょう。 答えは、R1CSの制約を個別にチェックする代わりに、多項式でポイント取得テストを実行することにより、すべての制約を同時にチェックできるようになったことです。

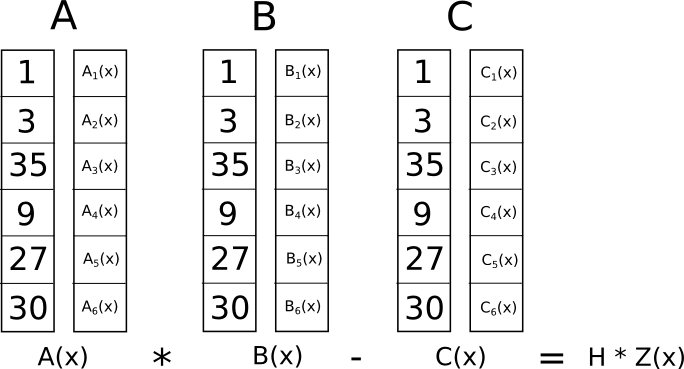
この場合、「ポイント取得」チェックは一連の多項式の加算と乗算であるため、結果自体は多項式になります。 論理遷移を表すために上記で使用した各x



座標で得られた多項式がゼロに等しい場合、これはすべてのチェックに合格することを意味します。 結果の多項式が、論理遷移を表すx



座標の少なくとも1つで非ゼロ値を与える場合、これは、この論理遷移に対して入力値と出力値が矛盾していることを意味します（たとえば、遷移y = x*sym_1



、および値が提供されます、たとえば、 x = 2



、 sym_1 = 2



およびy = 5



）。

結果の多項式は、どの値に対してもゼロにならないことに注意してください。 通常、ほとんどの場合、値はゼロとは異なります。 その動作は、論理的な遷移以外の点で可能ですが、論理的な遷移に実際に対応するすべての点で値ゼロをとる必要があります。 解全体の正確性を検証するために、遷移に対応する各点で多項式t = As * Bs - Cs



を評価しません。 代わりに、 t



を別の多項式Z



除算し、 Z



がt



完全に除算することを確認します。つまり、 t / Z



除算が剰余なしで発生します。

Z



(x - 1) * (x - 2) * (x - 3) ...



として定義され(x - 1) * (x - 2) * (x - 3) ...



は、論理遷移に対応するすべての点でゼロに等しい最も単純な多項式です。 数学から知られているように、これらのすべての点でゼロに等しい多項式は、これらの点の「最小」多項式の倍数でなければなりません。 逆に、多項式がZ



倍数である場合、これらのポイントのいずれかでの値はゼロになります。 この等価性により、計算が簡単になります。

それでは、上記の多項式を使ってポイント取得テストを行いましょう。 まず、中間多項式：

 As = [43.0, -73.333, 38.5, -5.166] Bs = [-3.0, 10.333, -5.0, 0.666] Cs = [-41.0, 71.666, -24.5, 2.833]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

As * Bs - Cs



計算します。

 t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

「最小」多項式Z = (x - 1) * (x - 2) * (x - 3) * (x - 4)



を計算します。

 Z = [24, -50, 35, -10, 1]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

上記の結果をZで割ると、次のようになります。

 h = t / Z = [-3.666, 17.055, -3.444]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ご覧のとおり、トレースなし。

したがって、QAPのソリューションがあります。 このQAPソリューションに対して受け取ったR1CSソリューションの変数のいずれかを変更しようとすると、たとえば、最後の値を30ではなく31に設定すると、チェックの1つに合格しない多項式t



が得られます（この特定の場合、x =での結果3は0ではなく-1になります）。 さらに、 t



はZ



倍数にはなりません。 除算t / Z



は、残り[-5.0、8.833、-4.5、0.666]を提供します。

上記は簡略化されていることに注意してください。 「実世界」の加算では、乗算、減算、除算は通常の数ではなく、有限体の要素で発生します-自己矛盾のないひどい種類の算術です。したがって、私たちが知っていて愛するすべての代数則はまだ有効です。 しかし、すべての答えには、有限サイズのセットの要素があります。通常は、nに対して0〜n-1の範囲の整数です。 たとえば、n = 13の場合、1/2 = 7（および7 2 = 1）、3 5 = 2などです。

有限体演算を使用すると、丸め誤差を心配する必要がなくなり、システムが楕円曲線でうまく動作できるようになります。これは、zk-SNARKsプロトコルを事実上安全にする残りのzk-SNARKsに最終的に必要です。

zk-SNARKの内部動作に関する多くの詳細を説明してくれたEran Tromerに特に感謝します。