記事の最初の部分は、レイトレーサーがシンプルで直感的なアルゴリズムのみを使用して驚くほど美しい画像を作成できるソフトウェアのエレガントな例であることを証明できます。



残念ながら、この単純さには代償が伴います。パフォーマンスが低下します。 レイトレーサーの最適化と並列化には多くの方法がありますが、リアルタイムで実行するには計算上のコストがかかりすぎます。 そして、機器は進化を続け、毎年より高速になっていますが、アプリケーションの一部の分野では美しいですが、 今日では数百倍の高速の作成画像が必要です 。 これらすべてのアプリケーション分野のうち、最も要求が厳しいのはゲームです。1秒あたり少なくとも60フレームの頻度で優れた画像をレンダリングすることを期待しています。 レイトレーサーはそれを処理できません。



それでは、ゲームはどのように成功しますか？



答えは、まったく異なるアルゴリズムファミリを使用することにあります。これについては、記事の後半で検討します。 人間の目やカメラでの画像形成の単純な幾何学的モデルから得られたレイトレーシングとは異なり、今度はもう一方の端から始めます-画面に何を描画できるか、できるだけ早く描画する方法を自問します。 その結果、ほぼ同様の結果を作成する完全に異なるアルゴリズムが得られます。

直接

ゼロから始めましょう：寸法を持つキャンバスがあります $$$C_w$ そして $$$C_h$ 、ピクセルを配置できます（ $$$PutPixel（）$ ）



2つのポイントがあるとしましょう。 $$$P_0$ そして $$$P_1$ 座標付き $$$（x_0、y_0）$ そして $$$（x_1、y_1）$ 。 これらの2つの点を別々に描くのは簡単です。 しかし、どのようにして直線セグメントを描くことができますか $$$P_0$ で $$$P_1$ ？



最初に光線で行ったように、パラメトリック座標で直線を表示することから始めましょう（これらの「光線」は3Dの直線にすぎません）。 ライン上の任意のポイントは、 $$$P_0$ から少し離れて $$$P_0$ に $$$P_1$ ：

$$

$$P = P_0 + t（P_1-P_0）$$

この方程式を、座標ごとに1つずつ、2つに分解できます。

$$

$$x = x_0 + t（x_1-x_0）$$

$$

$$y = y_0 + t（y_1-y_0）$$

最初の方程式を取り、計算しましょう $$$t$ ：

$$

$$x = x_0 + t（x_1-x_0）$$

$$

$$x-x_0 = t（x_1-x_0）$$

$$

$${{x-x_0} \ over {x_1-x_0}} = t$$

これで、代わりに2番目の式でこの式を置き換えることができます $$$t$ ：

$$

$$y = y_0 + t（y_1-y_0）$$

$$

$$y = y_0 + {{x-x_0} \ over {x_1-x_0}}（y_1-y_0）$$

少し変換します。

$$

$$y = y_0 +（x-x_0）{{y_1-y_0} \ over {x_1-x_0}}$$

に注意してください $$${{y_1-y_0} \ over {x_1-x_0}}$ -セグメントのエンドポイントのみに依存する定数です。 それを示しましょう $$$a$ ：

$$

$$y = y_0 + a（x-x_0）$$

なに $$$a$ ？ 決定方法から判断すると、それは座標の変化の指標です $$$y$ 座標の単位長を変更するには $$$x$ ; 言い換えれば、それは線の勾配の指標です。



方程式に戻りましょう。 括弧を開きましょう：

$$

$$y = y_0 + ax-ax_0$$

定数をグループ化します。

$$

$$y = ax +（y_0-ax_0）$$

表現 $$$（y_0-ax_0）$ この場合も、セグメントのエンドポイントのみに依存します。 それを示しましょう $$$b$ そして最後に

$$

$$y = ax + b$$

これは古典的な線形関数であり、ほぼすべての線で表すことができます。 値が無限にあるため、垂直線を説明できません $$$y$ ある値で $$$x$ 、他のすべてと1つではありません。 初期パラメトリック方程式からそのような表現を取得するプロセスでは、そのようなラインファミリが欠落する場合があります。 これは計算時に起こります $$$t$ 何を無視したから $$$x_1-x_0$ ゼロによる除算を行うことができます。 とりあえず、縦線を無視しましょう。 後でこの制限を取り除きます。



これで値を計算する方法ができました $$$y$ 興味のある価値について $$$x$ 。 この場合、カップルを取得します $$$（x、y）$ 線の方程式を満たす。 から移動する場合 $$$x_0$ に $$$x_1$ 値を計算します $$$y$ 各値に対して $$$x$ 、その後、線を描く関数の最初の近似を取得します。

DrawLine(P0, P1, color) { a = (y1 - y0)/(x1 - x0) b = y0 - a*x0 for x = x0 to x1 { y = a*x + b canvas.PutPixel(x, y, color) } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このフラグメントでは、 x0



とy0



は座標です $$$x$ そして $$$y$ ポイントP0



; 将来、この便利なエントリを使用します。 また、除算演算子/



は整数除算ではなく、実数の除算を実行する必要があることに注意してください。



この関数は、上記の方程式の単純な単純な解釈であるため、機能することは明らかです。 しかし、私たちは彼女の仕事をスピードアップできますか？



値を計算しないことに注意してください $$$y$ すべてのために $$$x$ ：実際には、整数の増分としてのみ計算します $$$x$ 、次の順序で実行します：計算直後 $$$y（x）$ 計算する $$$y（x + 1）$ ：

$$

$$y（x）= ax + b$$

$$

$$y（x + 1）= a（x + 1）+ b$$

これを使用して、より高速なアルゴリズムを作成できます。 の違いを見てみましょう $$$y$ 連続したピクセル：

$$

$$y（x + 1）-y（x）=（a（x + 1）+ b）-（ax + b）$$

$$

$$= a（x + 1）+ b-ax-b$$

$$

$$= ax + a-ax$$

$$

$$= a$$

これはそれほど驚くことではありません。 最後の傾きで $$$a$ 方法の指標です $$$y$ 増分単位ごとの変更 $$$x$ 、それがまさに私たちがここでやっていることです。



興味深いことに、次のものを簡単に取得できます。

$$

$$y（x + 1）= y（x）+ a$$

これは、次の値を計算できることを意味します $$$y$ 前の値のみを使用する $$$y$ 傾きを追加します。 ピクセルごとの乗算は不要です。 どこかから始める必要があります（最初は「以前の価値 $$$y$ "、だから私たちはで始まります $$$（x_0、y_0）$ 、そして追加します $$$1$ に $$$x$ そして $$$a$ に $$$y$ に達するまで $$$x_0$ 。



それを信じて $$$x_0 <x_1$ 、関数を次のように書き換えることができます。

 DrawLine(P0, P1, color) { a = (y1 - y0)/(x1 - x0) y = y0 for x = x0 to x1 { canvas.PutPixel(x, y, color) y = y + a } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この新しいバージョンの関数には、新しい制限があります。左から右にのみ直線を描画できます。 $$$x_0 <x_1$ 。 この問題を回避するのは非常に簡単です。個々のピクセルを描画する順序は関係ないので、右から左に線がある場合は、 P0



とP1



を変更して同じ線の左右バージョンに変えてから、前：

 DrawLine(P0, P1, color) { # Make sure x0 < x1 if x0 > x1 { swap(P0, P1) } a = (y1 - y0)/(x1 - x0) y = y0 for x = x0 to x1 { canvas.PutPixel(x, y, color) y = y + a } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、いくつかの線を描くことができます。 ここに $$$（-200、100）-（240、120）$ ：







彼女の様子は次のとおりです。







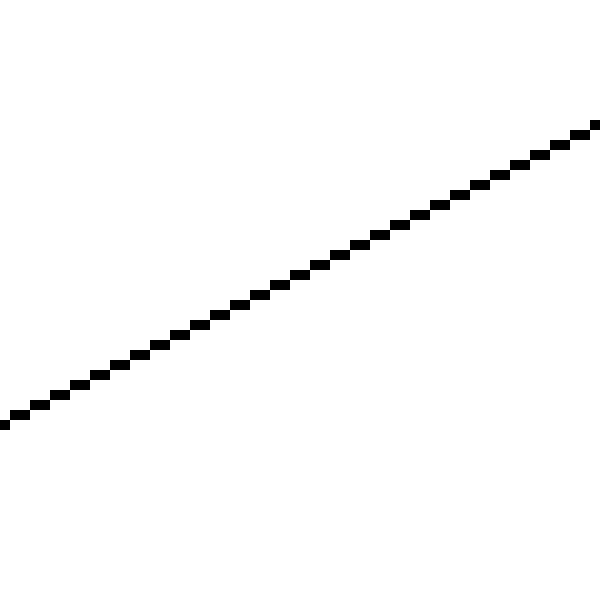
整数座標でしかピクセルを描画できないため、線が壊れているように見えます。数学的な線の幅は実際にはゼロです。 私たちが描くのは、理想的な線への離散化された近似です $$$（-200、100）-（240、120）$ （注：より美しい近似線を描画する方法があります。2つの理由で使用しません：1）遅い、2）私たちの目標は美しい線を描画するのではなく、3Dシーンをレンダリングする基本的なアルゴリズムを開発することです。）



別の線を引きましょう $$$（-50、-200）-（60、240）$ ：







そしてここに彼女がどのように見えるかがあります：







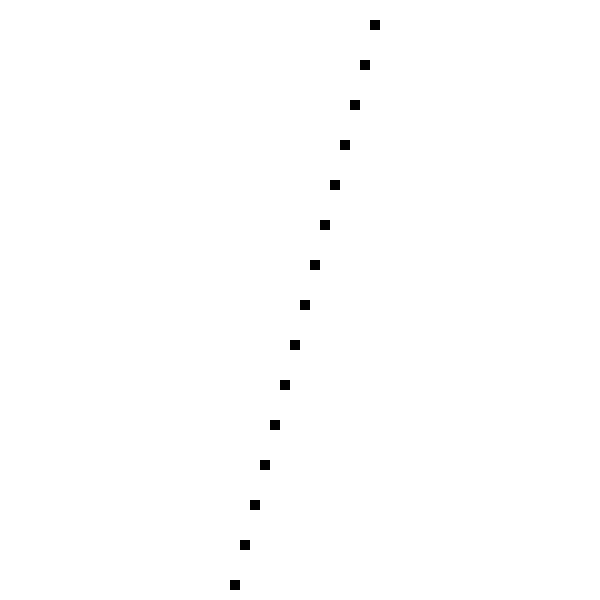
痛い。 どうした



アルゴリズムは意図したとおりに機能しました。 彼は左から右に行き、値を計算しました $$$y$ 各値に対して $$$x$ 対応するピクセルを描画しました。 問題は、彼が単一の値を計算したことです $$$y$ 各値に対して $$$x$ 、一部の値では $$$x$ いくつかの値が必要です $$$y$ 。



これは、次の文言の選択の直接的な結果です。 $$$y = f（x）$ ; 実際、同じ理由で、垂直線を描画することはできません。これは、1つの値がある制限的な場合です $$$x$ 複数の意味を持つ $$$y$ 。



問題なく水平線を描画できます。 垂直線を簡単に描画できないのはなぜですか？



結局のところ、私たちはそれを行うことができます。 選択肢 $$$y = f（x）$ arbitrary意的な決定でしたので、直接を表現する理由はありません $$$x = f（y）$ すべての方程式を処理して変更する $$$x$ そして $$$y$ 結果として次のアルゴリズムを取得します。

 DrawLine(P0, P1, color) { # Make sure y0 < y1 if y0 > y1 { swap(P0, P1) } a = (x1 - x0)/(y1 - y0) x = x0 for y = y0 to y1 { canvas.PutPixel(x, y, color) x = x + a } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これは、計算の場所を変更することを除いて、以前のDrawLine



似ています $$$x$ そして $$$y$ 。 結果の関数は垂直線を処理でき、正しく描画できます $$$（0、0）-（50、100）$ ; もちろん、彼女は水平線に対応せず、正しく描画することはできません $$$（0、0）-（100、50）$ ！ どうする？



描画する線に応じて、適切なバージョンの関数を選択するだけです。 そして、基準は非常に簡単です。 行にはもっと異なる意味がありますか $$$x$ または $$$y$ ？ さらに値がある場合 $$$x$ より $$$y$ 、最初のバージョンを使用します。 それ以外の場合は、2番目が適用されます。



すべてのケースを処理するDrawLine



のバージョンは次のとおりです。

 DrawLine(P0, P1, color) { dx = x1 - x0 dy = y1 - y0 if abs(dx) > abs(dy) { #     # ,  x0 < x1 if x0 > x1 { swap(P0, P1) } a = dy/dx y = y0 for x = x0 to x1 { canvas.PutPixel(x, y, color) y = y + a } } else { #     # ,  y0 < y1 if y0 > y1 { swap(P0, P1) } a = dx/dy x = x0 for y = y0 to y1 { canvas.PutPixel(x, y, color) x = x + a } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これは確かに機能しますが、コードは特に美しくはありません。 線形関数を増分的に計算する2つのコード実装があり、この計算と選択のロジックは混在しています。 線形関数を使用することが多いため、コードの分離に少し時間をかける価値があります。



2つの機能があります。 $$$y = f（x）$ そして $$$x = f（y）$ 。 ピクセルを扱うという事実を無視するために、一般的な方法で次のように書きましょう。 $$$d = f（i）$ どこで $$$i$ 値を選択する独立変数であり、 $$$d$ -値が別のものに依存し、計算したい従属変数 。 より水平な線の場合 $$$x$ 独立変数であり、 $$$y$ -依存; より垂直な線の場合、逆のことが当てはまります。



もちろん、関数は次のように書くことができます $$$d = f（i）$ 。 それを完全に定義するもう2つの側面を知っています。その直線性と2つの意味です。 すなわち $$$d_0 = f（i_0）$ そして $$$d_1 = f（i_1）$ 。 これらの値を受け取り、中間値を返す簡単なメソッドを書くことができます $$$d$ 前と同じように、 $$$i1 <i0$ ：

 Interpolate (i0, d0, i1, d1) { values = [] a = (d1 - d0) / (i1 - i0) d = d0 for i = i0 to i1 { values.append(d) d = d + a } return values }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

値に注意してください $$$d$ 対応する $$$i_0$ 、 values[0]



、値は $$$i_0 + 1$ values[1]



などにあります。 一般的な意味 $$$i_n$ values[i_n - i_0]



にあると仮定すると、 $$$i_n$ 範囲内にある $$$[i_0、i_1]$ 。



考慮すべき行き止まりのケースがあります。 計算する必要があるかもしれません $$$d = f（i）$ 単一の意味のために $$$i$ 、つまり $$$i0 = i1$ 。 この場合、計算すらできません $$$a$ 、これを特別なケースとして扱います：

 Interpolate (i0, d0, i1, d1) { if i0 == i1 { return [ d0 ] } values = [] a = (d1 - d0) / (i1 - i0) d = d0 for i = i0 to i1 { values.append(d) d = d + a } return values }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、 Interpolate



を使用してDrawLine



を作成できます。

 DrawLine(P0, P1, color) { if abs(x1 - x0) > abs(y1 - y0) { #     # ,  x0 < x1 if x0 > x1 { swap(P0, P1) } ys = Interpolate(x0, y0, x1, y1) for x = x0 to x1 { canvas.PutPixel(x, ys[x - x0], color) } } else { #     # ,  y0 < y1 if y0 > y1 { swap(P0, P1) } xs = Interpolate(y0, x0, y1, x1) for y = y0 to y1 { canvas.PutPixel(xs[y - y0], y, color) } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このDrawLine



は、すべてのケースを正しく処理できます。







ソースコードと作業デモ>>



このバージョンは前のものよりもそれほど短くはありませんが、中間値の計算を明確に分離しています $$$y$ そして $$$x$ 、独立変数とレンダリングコード自体を選択する決定。 この利点は完全には明らかではないかもしれませんが、以降の章で再び積極的にInterpolate



を使用します。



これは最良または最速のレンダリングアルゴリズムではないことに注意してください。 この章の重要な結果はDrawLine



ではなくInterpolate



でした。 線を描くのに最適なアルゴリズムは、おそらくブレゼンハムアルゴリズムです。

塗りつぶされた三角形

DrawLine



メソッドを使用して、三角形の輪郭を描くことができます。 このタイプの輪郭は、三角形のワイヤフレームのように見えるため、 ワイヤフレームと呼ばれます。

 DrawWireframeTriangle (P0, P1, P2, color) { DrawLine(P0, P1, color); DrawLine(P1, P2, color); DrawLine(P2, P0, color); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次の結果が得られます。







三角形を何らかの色で塗りつぶすことはできますか？



コンピュータグラフィックスで通常起こるように、これを行うには多くの方法があります。 塗りつぶされた三角形を描画し、それらを水平線のセグメントのセットとして認識します。それらが一緒に描画されると、三角形のように見えます。 以下は、私たちがやりたいことの非常に大まかな最初の近似です。

    y  ,    x_left  x_right   y DrawLine(x_left, y, x_right, y)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

「三角形が占める水平線の各y座標について」の部分から始めましょう。 三角形は3つの頂点によって定義されます $$$P_0$ 、 $$$P_1$ そして $$$P_2$ 。 値を増やしてこれらのポイントを並べ替える場合 $$$y$ そのような方法で $$$y_0 \ le y_1 \ le y_2$ 、次に値の範囲 $$$y$ 三角形に占有されることは等しくなります $$$[y_0、y_2]$ ：

 if y1 < y0 { swap(P1, P0) } if y2 < y0 { swap(P2, P0) } if y2 < y1 { swap(P2, P1) }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、 x_left



とx_right



を計算する必要がありx_right



。 三角形には2つの辺ではなく3つの辺があるため、これはもう少し複雑です。 ただし、値の面で $$$y$ 私たちは常に「長い」側面を持っています $$$P_0$ 前に $$$P_2$ および2つの「短い」辺 $$$P_0$ 前に $$$P_1$ そしてから $$$P_1$ lj $$$P_2$ （注：特別な場合があります $$$y_0 = y_1$ または $$$y_1 = y_2$ つまり、三角形の横辺がある場合。 このような場合、「長い」側面と見なされる2つの側面があります。 幸いなことに、どちらを選択するかは問題ではないため、この定義に固執できます。 つまり、 x_right



値は、 x_right



または両方の短辺から取得されます。 およびx_left



値x_left



別のセットから取得されます。



値を計算することから始めます $$$x$ 三方用。 水平セグメントを描画するため、正確に1つの値が必要です $$$x$ 各値に対して $$$y$ ; これは、独立した値として使用して、 Interpolate



を使用して直接値を取得できることを意味します $$$y$ 、および依存値として $$$x$ ：

 x01 = Interpolate(y0, x0, y1, x1) x12 = Interpolate(y1, x1, y2, x2) x02 = Interpolate(y0, x0, y2, x2)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

x02



はx_left



またはx_right



いずれかx_right



。 もう1つはx01



とx12



連結です。



これらの2つのリストには重複する値があることに注意してください。 $$$x$ のために $$$y_1$ x01



の最後の値とx12



最初の値の両方です。 そのうちの1つを取り除くだけです。

 remove_last(x01) x012 = x01 + x12
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最後に、 x02



とx012



がx02



、 x012



がx02



とx012



であるかを決定する必要がありx_right



。 これを行うには、値を見てください $$$x$ 行の1つ、たとえば中央の場合：

 m = x02.length / 2 if x02[m] < x012[m] { x_left = x02 x_right = x012 } else { x_left = x012 x_right = x02 }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

現在は、水平セグメントのみを描画します。 後で明らかになる理由のため、これにはDrawLine



を使用しません。 代わりに、ピクセルを個別に描画します。



DrawFilledTriangle



の完全版はDrawFilledTriangle



です。

 DrawFilledTriangle (P0, P1, P2, color) { #   ,  y0 <= y1 <= y2 if y1 < y0 { swap(P1, P0) } if y2 < y0 { swap(P2, P0) } if y2 < y1 { swap(P2, P1) } #   x   x01 = Interpolate(y0, x0, y1, x1) x12 = Interpolate(y1, x1, y2, x2) x02 = Interpolate(y0, x0, y2, x2) #    remove_last(x01) x012 = x01 + x12 # ,       m = x012.length / 2 if x02[m] < x012[m] { x_left = x02 x_right = x012 } else { x_left = x012 x_right = x02 } #    for y = y0 to y2 { for x = x_left[y - y0] to x_right[y - y0] { canvas.PutPixel(x, y, color) } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結果は次のとおりです。 検証のために、 DrawWireframeTriangle



をDrawWireframeTriangle



てから、同じ座標で異なる色のDrawWireframeTriangle



をDrawWireframeTriangle



ました。







ソースコードと作業デモ>>



三角形の黒い輪郭が緑の内側の領域と完全に一致しないことに気付くかもしれません。 これは、三角形の右下の端で特に顕著です。 DrawLine（）が計算するために起こりました $$$y = f（x）$ このエッジに対して、DrawTriangle（）は計算します $$$x = f（y）$ 。 高速レンダリングという目標を達成するために、このような近似を行う準備ができています。

影付きの三角形

前のパートでは、三角形を描画して色で塗りつぶすためのアルゴリズムを開発しました。 次の目標は、グラデーションであふれているように見える陰影付きの三角形を描くことです。



影付きの三角形はモノクロの三角形よりもきれいに見えますが、これはこの章の主な目的ではありません。 これは、私たちが作成するテクノロジーの特別なアプリケーションです。 おそらく、記事のこのセクションで最も重要になるでしょう。 他のほとんどすべては、その基礎に基づいて構築されます。



しかし、簡単なものから始めましょう。 三角形を単色で塗りつぶす代わりに、色の濃淡で塗りつぶします。 次のようになります。







ソースコードと作業デモ>>



最初のステップは、レンダリングするものを正式に定義することです。 これを行うには、各頂点に実際の値を割り当てます $$$h$ 頂点の色の明るさを示します。 $$$h$ 範囲内にある $$$[0.0、1.0]$ 。



ピクセルの正確な色を取得するには、色を $$$C$ と明るさ $$$h$ 、単純にチャネルごとの乗算を実行します。 $$$C_h =（R_C * h、G_C * h、B_C * h）$ 。 つまり、 $$$h = 0.0$ 私たちは黒くなる、そしていつ $$$h = 1.0$ -元の色 $$$C$ 。

エッジシェーディングの計算

したがって、影付きの三角形を描くには、値を計算する必要があります $$$h$ 三角形のピクセルごとに、適切な色かぶりを取得してピクセルを塗りつぶします。 すべてが非常に簡単です！



ただし、この段階では値のみを知っています $$$h$ 与えられた頂点に対して。 値の計算方法 $$$h$ 三角形の残りの部分は？



最初にrib骨を見てみましょう。 エッジを選択 $$$AB$ 。 知ってる $$$h_A$ そして $$$h_B$ 。 で何が起こる $$$M$ 、つまりセグメントの中央に $$$AB$ ？ 明るさを $$$A$ に $$$B$ それから $$$h_M$ 間の値である必要があります $$$h_A$ そして $$$h_B$ 。 以来 $$$M$ セグメントの中点です $$$AB$ それならどうして $$$h_M$ 平均値 $$$h_A$ そして $$$h_B$ ？



より正式に言えば、関数があります $$$h = f（P）$ 限界値を知っている $$$h（A）$ そして $$$h（B）$ それをスムーズにする必要があります。 私たちは他に何も知りません $$$h = f（P）$ したがって、これらの基準を満たす任意の関数、たとえば線形関数を選択できます。







もちろん、影付きの三角形のコードの基礎は、前の章で作成された実線の三角形のコードになります。 最初のステップの1つは、各水平セグメントの端点、つまりx_left



およびx_right



を伴います $$$P_0P_1$ 、 $$$P_0P_2$ そして $$$P_1P_2$ ; Interpolate()



を使用して値を計算しました $$$x = f（y）$ 持っている $$$x（y_0）$ そして $$$x（y_1）$ ...それがまさにここでやりたいことです。それを置き換えるだけです $$$x$ に $$$h$ ！



つまり、中間値を計算できます $$$h$ 値を計算したのとまったく同じ方法で $$$x$ ：

 x01 = Interpolate(y0, x0, y1, x1) h01 = Interpolate(y0, h0, y1, h1) x12 = Interpolate(y1, x1, y2, x2) h12 = Interpolate(y1, h1, y2, h2) x02 = Interpolate(y0, x0, y2, x2) h02 = Interpolate(y0, h0, y2, h2)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次のステップでは、これらの3つのベクトルを2つのベクトルに変換し、どちらが左側の値を表し、どちらが右側の値を表すかを決定します。 値に注意してください $$$h$ それが何であるかに関与しません。 値によって完全に決定されます $$$x$ 。 値 $$$h$ 価値への「こだわり」 $$$x$ それらは同じ物理ピクセルの他の属性だからです。 つまり、 x012



三角形の右側の値がある場合、 x012



は三角形の右側の値があります。

  #    remove_last(x01) x012 = x01 + x12 remove_last(h01) h012 = h01 + h12 # ,       m = x012.length / 2 if x02[m] < x012[m] { x_left = x02 x_right = x012 h_left = h02 h_right = h012 } else { x_left = x012 x_right = x02 h_left = h012 h_right = h02 }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

内部シェーディングの計算

残っている唯一のステップは、水平セグメント自体を描画することです。 各セグメントについて $$$x_ {左}$ そして $$$x_ {right}$ そして今、私たちも知っています $$$h_ {左}$ そして $$$h_ {right}$ 。 ただし、左から右に繰り返して各ピクセルを基本色でレンダリングする代わりに、値を計算する必要があります $$$h$ セグメントの各ピクセルに対して。



再び仮定することができます $$$h$ と線形に変化する $$$x$ Interpolate()



を使用してこれらの値を計算します。

 h_segment = Interpolate(x_left[y-y0], h_left[y-y0], x_right[y-y0], h_right[y-y0])
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして今では、各ピクセルの色を計算してレンダリングするだけです。



DrawShadedTriangle



の計算コードはDrawShadedTriangle



です。

 DrawShadedTriangle (P0, P1, P2, color) { #   ,  y0 <= y1 <= y2 if y1 < y0 { swap(P1, P0) } if y2 < y0 { swap(P2, P0) } if y2 < y1 { swap(P2, P1) } #   x   h    x01 = Interpolate(y0, x0, y1, x1) h01 = Interpolate(y0, h0, y1, h1) x12 = Interpolate(y1, x1, y2, x2) h12 = Interpolate(y1, h1, y2, h2) x02 = Interpolate(y0, x0, y2, x2) h02 = Interpolate(y0, h0, y2, h2) #    remove_last(x01) x012 = x01 + x12 remove_last(h01) h012 = h01 + h12 # ,       m = x012.length / 2 if x02[m] < x012[m] { x_left = x02 x_right = x012 h_left = h02 h_right = h012 } else { x_left = x012 x_right = x02 h_left = h012 h_right = h02 } #    for y = y0 to y2 { x_l = x_left[y - y0] x_r = x_right[y - y0] h_segment = Interpolate(x_l, h_left[y - y0], x_r, h_right[y - y0]) for x = x_l to x_r { shaded_color = color*h_segment[x - xl] canvas.PutPixel(x, y, shaded_color) } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このアルゴリズムは、見た目よりもはるかに一般的です。つまり、 $$$h$ 色を掛けて、何 $$$h$ 色の明るさは、何の役割も果たしていません。 これは、この手法を使用して、三角形の各ピクセルの実数として表すことができるものの値を計算できることを意味します。三角形の頂点でこのプロパティの値から始め、プロパティが画面上で線形に変化すると仮定します。



したがって、このアルゴリズムは後続の部分で非常に貴重であることがわかります。 よく理解できるまで読み続けないでください。

透視投影

しばらくの間、2Dの三角形をそのままにして、3Dに注意を払います。 より具体的には、2Dサーフェス上で3Dオブジェクトをどのように表現できるか。



レイトレーシング部分の最初に行ったのと同じ方法で、 カメラを設定することから始めます 。 同じ条件を使用します：カメラは $$$O =（0、0、0）$ に向かって $$$\ vec {Z _ +}$ 、アップベクトルは $$$\ vec {Y _ +}$ 。 長方形のビューポートサイズも定義します $$$V_w$ に $$$V_h$ エッジが平行である $$$\ vec {X}$ そして $$$\ vec {Y}$ そして離れて $$$d$ カメラから。 このいずれかが明確でない場合は、 レイトレーシングの基本の章をお読みください。



ポイントを考慮してください $$$P$ カメラの前のどこかに。 カメラは「見る」 $$$P$ 、つまり、特定の光線が反射します $$$P$ カメラに到達します。 ポイントを見つけることに興味があります $$$P '$ 、光線がビューポートを横切る（ビューアー内のポイントから開始して光線を通して見えるものを決定するとき、光線をトレースするときのアクションの反対であることに注意してください）：







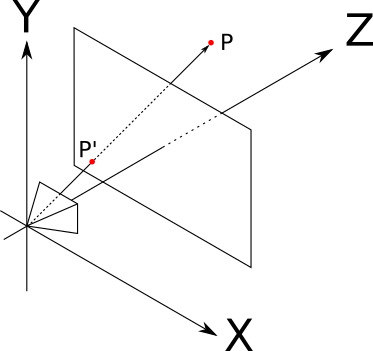
これが「右側」に見える状況の図です。つまり、 $$$\ vec {Y _ +}$ 上向き $$$\ vec {Z _ +}$ 右に向けて $$$\ vec {X _ +}$ 私たちに向けて：







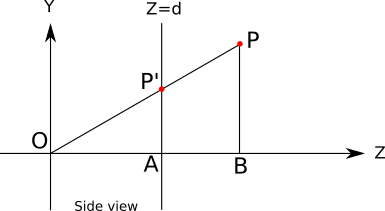
に加えて $$$O$ 、 $$$P$ そして $$$P '$ この図にポイントが示されています $$$A$ そして $$$B$ 状況を理解するのに役立ちます。



それは明らかです $$$P'_Z = d$ 私たちが決定したので $$$P '$ ビューポート内のポイントであり、ビューポートが平面上にある $$$Z = d$ 。



また、三角形が $$$OP'A$ そして $$$OPB$ 同様：共通点が2つあります $$$Oa$ 同様の $$$Ob$ 、そして $$$OP$ 同様の $$$OP '$ ）そして残りの辺は平行です（ $$$P'A$ そして $$$PB$ ） これは、次の比例方程式が成り立つことを意味します。

$$

$${|P'A| \over |OA|} = {|PB| \over |OB|}$$

それから私たちは得る

$$

$$|P'A| = {|PB| \cdot |OA| \over {|OB|}}$$

この方程式の各セグメント（符号付き）の長さは、既知のポイントまたは必要なポイントの座標です。 $$$|P'A| = P'_Y$ 、 $$$|PB| = P_Y$ 、 $$$|OA| = P'_Z = d$ そして $$$|OB| = P_Z$ 。 それらを上記の方程式に代入すると、

$$

$$P'_Y = {P_Y \cdot d \over P_Z}$$

今度は上から同様の図を描くことができます： $$→ Z +は上向きで、$\vec{Z_+}$$$→ X +は右に向けられ、$\vec{X_+}$$$→ Y +は私たちを対象としています：これらの三角形を再び使用すると、$\vec{Y_+}$

$$

$$P'_X = {P_X \cdot d \over P_Z}$$

投影方程式

すべて一緒にしましょう。ポイントを指定する場合$$シーンの Pおよびカメラと表示ウィンドウの標準設定、投影$P$$$P我々はとして指定プレビューウィンドウで、$P$$$P 'は次のように計算できます。$P'$

$$

$$P'_X = {P_X \cdot d \over P_Z}$$

$$

$$P'_Y = {P_Y \cdot d \over P_Z}$$

$$

$$P'_Z = d$$

ここで最初に行うことは、次のことを忘れることです $$$P'_Z$ ;定義による値は一定であり、3Dから2Dに移行しようとしています。



今$$P ′は空間の点のままです。その座標は、ピクセルではなく、シーンの記述に使用される単位で指定されます。ビューポートの座標からキャンバスの座標への変換は非常に簡単で、「レイトレーシング」部分で使用した変換「canvas-viewport」とはまったく逆です。$P'$

$$

$$C_x = V_x \cdot {C_w \over V_w}$$

$$

$$C_y = V_y \cdot {C_h \over V_h}$$

最後に、シーン内のポイントから画面上のピクセルに移動できます！

射影方程式のプロパティ

射影方程式には、議論する価値のある興味深い特性があります。



第一に、一般的に、それは直観的であり、実生活の経験と一致しています。オブジェクトが右側にあるほど（$$X）、右側に表示されるほど（$X$$$X ′が増加します）。同じことが当てはまります$X'$$$$Y$ そして $$$Y'$ 。 さらに、オブジェクトが遠いほど（増加します $$Z）、見た目が少ないほど（つまり、$Z$$$$X'$ そして $$Y ′減少）。ただし、値が小さくなると、すべてが明確になりません。$Y'$



$$$Z$ ; 負の値で $$Z、つまり、オブジェクトがカメラの後ろにある場合、オブジェクトは依然として投影されますが、上下が逆になります！そして、もちろん、いつ$Z$$$Z = 0、宇宙は崩壊します。どういうわけか、このような不快な状況を避ける必要があります。各ポイントはカメラの前にあると想定し、別の章でこれを扱います。透視投影のもう1つの基本的な特性は、1つの線に属する点を保持することです。つまり、表示ウィンドウ内の1つの直線に属する3つの点の投影も1つの直線に属します（注：この観察は簡単なように思えるかもしれませんが、たとえば、2つの直線間の角度が保持されないことに注意する価値があります。平行線が地平線、まるで道路の両側。）。つまり、直線は常に直線のように見えます。$Z = 0$







これは私たちにとって非常に重要です。ポイントを投影することについて話していましたが、ラインセグメントや三角形を投影することについてはどうでしょうか。このプロパティにより、ラインセグメントの投影は、エンドポイントの投影と接続するラインセグメントになります。したがって、ポリゴンを投影するには、頂点を投影し、結果のポリゴンを描画するだけで十分です。



したがって、最初の3Dオブジェクトであるキューブに移動して描画できます。 8つの頂点の座標を設定し、立方体のエッジを構成する12組の頂点の投影間に線を引きます。

  ViewportToCanvas(x, y) { return (x*Cw/Vw, y*Ch/Vh); } ProjectVertex(v) { return ViewportToCanvas(vx * d / vz, vy * d / vz) #  "" . vAf = [-1, 1, 1] vBf = [1, 1, 1] vCf = [1, -1, 1] vDf = [-1, -1, 1] #  "" . vAb = [-1, 1, 2] vBb = [1, 1, 2] vCb = [1, -1, 2] vDb = [-1, -1, 2] #  . DrawLine(ProjectVertex(vAf), ProjectVertex(vBf), BLUE); DrawLine(ProjectVertex(vBf), ProjectVertex(vCf), BLUE); DrawLine(ProjectVertex(vCf), ProjectVertex(vDf), BLUE); DrawLine(ProjectVertex(vDf), ProjectVertex(vAf), BLUE); #  . DrawLine(ProjectVertex(vAb), ProjectVertex(vBb), RED); DrawLine(ProjectVertex(vBb), ProjectVertex(vCb), RED); DrawLine(ProjectVertex(vCb), ProjectVertex(vDb), RED); DrawLine(ProjectVertex(vDb), ProjectVertex(vAb), RED); # ,     . DrawLine(ProjectVertex(vAf), ProjectVertex(vAb), GREEN); DrawLine(ProjectVertex(vBf), ProjectVertex(vBb), GREEN); DrawLine(ProjectVertex(vCf), ProjectVertex(vCb), GREEN); DrawLine(ProjectVertex(vDf), ProjectVertex(vDb), GREEN);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、我々はこのような何かを得る：







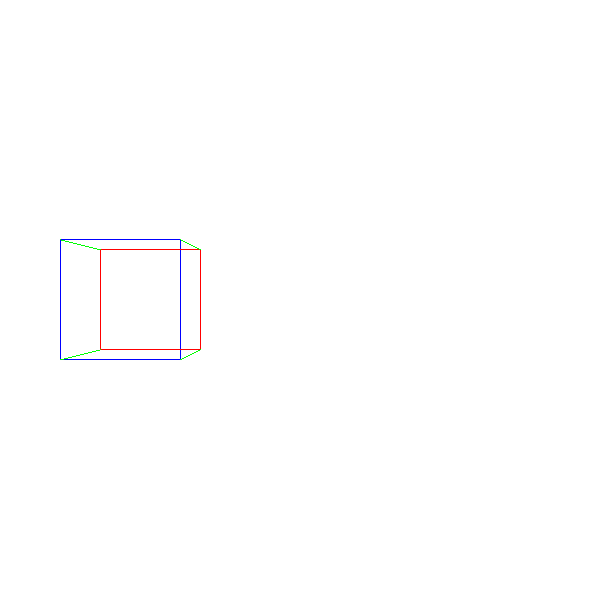
ソースコードと作業のデモを>>



この作品は、我々は深刻な問題を抱えていたものの-私たちは2つのキューブをレンダリングしたい場合は？キューブではなく、何か他のものをレンダリングしたい場合はどうでしょうか？プログラムが実行されていないときにレンダリングするものがわからない場合（たとえば、ディスクから3Dモデルをロードする場合）次の章では、これらすべての問題を解決する方法を学びます。

シーン設定

頂点の指定された座標でキャンバスに三角形を描画する技術と、三角形の3D座標をキャンバスの2D座標に変換する方程式を開発しました。この章では、三角形で構成されるオブジェクトの表現方法、およびそれらの操作方法を学習します。



このために、キューブを使用します。これは三角形から作成できる最も簡単な3Dオブジェクトではありませんが、いくつかの問題を説明するのに便利です。立方体のエッジは2単位の長さで、座標軸に平行であり、その中心は原点にあります：







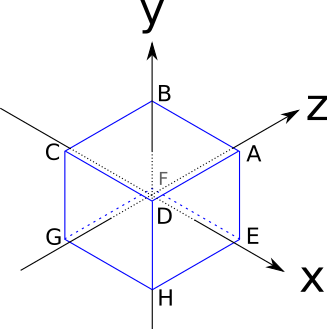
頂点の座標は次のとおりです。



$$$A = (1, 1, 1)$

$$$B = (-1, 1, 1)$

$$$C = (-1, -1, 1)$

$$$D = (1, -1, 1)$

$$$E = (1, 1, -1)$

$$$F = (-1, 1, -1)$

$$$G = (-1, -1, -1)$

$$H = （1 、- 1 、- 1 ）立方体の側面は正方形ですが、我々は三角形だけに対処する方法を知っています。問題はありません。どのポリゴンも多くの三角形に分解できます。したがって、キューブの各辺を2つの三角形の形で表します。もちろん、立方体の3つの頂点のすべてのセットが立方体の表面の三角形を表すわけではありません（たとえば、AGHは立方体の「内側」にあります）。これらの頂点で構成される三角形のリストも作成する必要があります。$H = (1, -1, -1)$

 A, B, C A, C, D E, A, D E, D, H F, E, H F, H, G B, F, G B, G, C E, F, B E, B, A C, G, H C, H, D
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これは、三角形で構成されるオブジェクトを表現するために使用できる構造があることを示しています。頂点座標のリストと、3つの頂点のセットがオブジェクトの三角形を形成することを決定する三角形のリストです。



三角形のリストの各エントリには、三角形に関する追加情報が含まれる場合があります。たとえば、各三角形の色を格納できます。



この情報を保存する最も自然な方法は2つのリストであるため、リストインデックスを頂点リストへのリンクとして使用します。つまり、上記のキューブは次のように表すことができます。

 Vertexes 0 = ( 1, 1, 1) 1 = (-1, 1, 1) 2 = (-1, -1, 1) 3 = ( 1, -1, 1) 4 = ( 1, 1, -1) 5 = (-1, 1, -1) 6 = (-1, -1, -1) 7 = ( 1, -1, -1) Triangles 0 = 0, 1, 2, red 1 = 0, 2, 3, red 2 = 4, 0, 3, green 3 = 4, 3, 7, green 4 = 5, 4, 7, blue 5 = 5, 7, 6, blue 6 = 1, 5, 6, yellow 7 = 1, 6, 2, yellow 8 = 4, 5, 1, purple 9 = 4, 1, 0, purple 10 = 2, 6, 7, cyan 11 = 2, 7, 3, cyan
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この方法で表されたオブジェクトのレンダリングは非常に簡単です。最初に各頂点を投影し、「投影された頂点」の一時リストに保存します。次に、三角形のリストを調べて、個々の三角形をレンダリングします。最初の近似では、次のようになります。

 RenderObject(vertexes, triangles) { projected = [] for V in vertexes { projected.append(ProjectVertex(V)) } for T in triangles { RenderTriangle(T, projected) } } RenderTriangle(triangle, projected) { DrawWireframeTriangle(projected[triangle.v[0]], projected[triangle.v[1]], projected[triangle.v[2]], triangle.color) }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このアルゴリズムをそのままキューブに適用して、正しい表示を期待することはできません。頂点の一部はカメラの背後にあります。そして、これはすでに見たように、奇妙な振る舞いにつながります。実際には、カメラがあるの内側キューブ。



したがって、キューブを移動するだけです。これを行うには、立方体の各頂点を一方向に移動するだけです。このベクトルを呼び出しましょう$$T、翻訳の略。立方体をカメラの前に正確に7ユニット前方に移動し、より面白く見えるように左に1.5ユニット移動します。前方が方向だから$T$$$→ Z +、および「左」-$\vec{Z_+}$$$→ X - 、変位ベクトルは、以下になり$\vec{X-}$

$$

$$\vec{T} = \begin{pmatrix} -1.5 \\ 0 \\ 7 \end{pmatrix}$$

移動したバージョンを取得するには $$各点の V '$V'$$$Vキューブ、変位ベクトルを追加するだけです。$V$

$$

$$V' = V + \vec{T}$$

この段階で、キューブを取得して各頂点を移動し、上記のアルゴリズムを適用して、最終的に最初の3Dキューブを取得できます。







ソースコードと作業デモ>>

モデルとインスタンス

しかし、2つのキューブをレンダリングする必要がある場合はどうでしょうか？



単純なアプローチは、2番目のキューブを記述する別の頂点と三角形のセットを作成することです。これは機能しますが、多くのメモリを消費します。そして、100万個のキューブをレンダリングしたい場合はどうでしょうか？モデルとインスタンスの



カテゴリーで考えるのがより賢くなるでしょう。モデルは、オブジェクトをそのまま記述する一連の頂点と三角形です（つまり、「立方体は次の一連の頂点と三角形で構成されます」）。一方、モデルインスタンスは、シーン内のある位置にあるモデルの具体的な実装です（つまり、「（0、0、5）に立方体があります」）。



2番目のアプローチの利点は、シーン内の各オブジェクトを一度だけ設定するだけで十分なことです。その後、任意の数のインスタンスをシーンに配置し、シーン内の位置を簡単に記述できます。



以下は、そのようなシーンをどのように説明できるかの大まかな近似です。

 model { name = cube vertexes { ... } triangles { ... } } instance { model = cube position = (0, 0, 5) } instance { model = cube position = (1, 2, 3) }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

レンダリングするには、インスタンスのリストを調べるだけです。インスタンスごとに、モデルの頂点のコピーを作成し、インスタンスの位置をそれらに適用して、以前のように動作します。

 RenderScene() { for I in scene.instances { RenderInstance(I); } } RenderInstance(instance) { projected = [] model = instance.model for V in model.vertexes { V' = V + instance.position projected.append(ProjectVertex(V')) } for T in model.triangles { RenderTriangle(T, projected) } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このアルゴリズムが機能するためには、モデルの頂点の座標は、オブジェクトの「論理」座標系で決定する必要があることに注意してください（これはモデル空間と呼ばれます）。たとえば、立方体は、その中心が（0、0、0）になるように定義されます。これは、「立方体が（1、2、3）にある」と言うとき、「立方体は（1、2、3）に対して中心にある」ことを意味します。モデル空間を指定する場合、厳密な規則はありません。主にアプリケーションに依存します。たとえば、人のモデルがある場合、その足の裏に原点を置くのが論理的です。移動した頂点は、シーンの「絶対」座標系（世界の空間と呼ばれる）で表現されます。



以下に2つのキューブを示します。







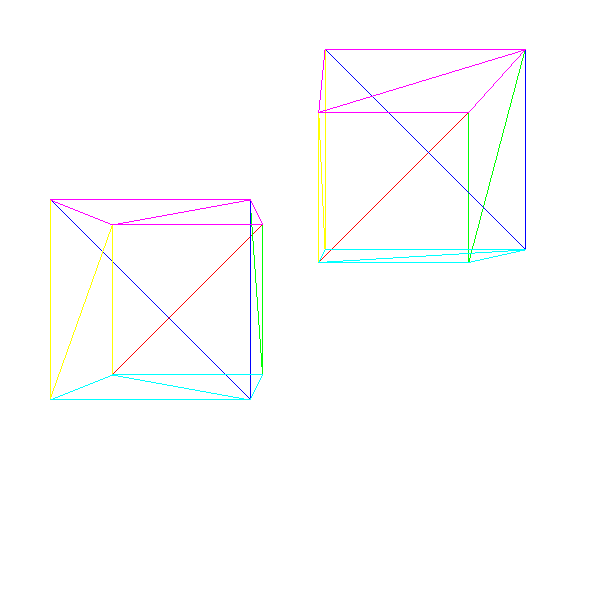
ソースコードと作業デモ>>

モデル変換

上記のシーンの定義により、かなり制限されます。特に、キューブの位置しか指定できないため、好きなだけキューブのインスタンスを作成できますが、それらはすべて同じ方向に向けられます。一般に、インスタンスをより詳細に制御する必要があります。また、方向と、場合によってはスケールを設定します。



概念的には、次の3つの要素でモデルの変換を正確に指定できます：スケールファクター、モデル空間の原点を基準とした回転、シーン内の特定のポイントへの移動：

 instance { model = cube transform { scale = 1.5 rotation = <45 degrees around the Y axis> translation = (1, 2, 3) } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

新しい変換を追加することにより、擬似コードの以前のバージョンを簡単に拡張できます。ただし、これらの変換が適用される順序は重要です。特に、移動は最後に実行する必要があります。ここにひねりがあります$$45 ∘軸Zに沿った動きが続く原点の周りに、：しかし、動きがターンに適用される：私たちは、より一般的なバージョンを書くことができます：$45^\circ$















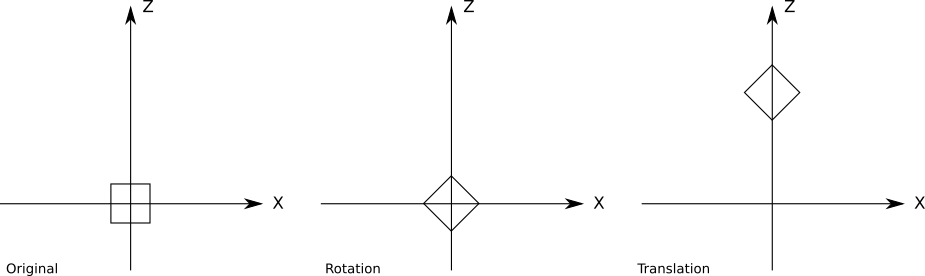
RenderInstance()

 RenderInstance(instance) { projected = [] model = instance.model for V in model.vertexes { V' = ApplyTransform(V, instance.transform); projected.append(ProjectVertex(V')) } for T in model.triangles { RenderTriangle(T, projected) } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

メソッドはApplyTransform()



次のとおりです。

 ApplyTransform(vertex, transform) { V1 = vertex * transform.scale V2 = V1 * transform.rotation V3 = V2 + transform.translation return V3 }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

回転は3x3マトリックスとして表されます。回転行列に慣れていない場合は、今のところ、3D回転は3x3行列によるポイントの積として表すことができると考えてください。線形代数の過程で詳細をご覧ください。

カメラ変換

前のセクションでは、シーン内のさまざまなポイントにモデルインスタンスを配置する方法を学びました。このセクションでは、シーン内でカメラを移動および回転する方法を学習します。



完全に空の座標系の真ん中にぶら下がっていると想像してください。すべてが黒く塗られています。突然、目の前に赤い立方体が現れます。しばらくすると、キューブが1ユニット近くに近づきます。しかし、キューブはあなたの近くに来ましたか？それとも、自分で1ユニットをキューブに移動しましたか？



開始点がなく、座標系が表示されていないため、何が起こったかを判断できません。



今、キューブはあなたの周りを回しました$$45 ∘時計回りに。$45^\circ$しかし、そうですか？ おそらくあなたは彼を振り向いた $$45 ∘反時計？繰り返しますが、これを判断することはできません。この思考実験により、固定されたシーンを横切ってカメラを移動しても、その周りを移動および回転するシーンで固定されたカメラを移動しても違いがないことがわかります！宇宙のこの明らかに利己的なビジョンの利点は、カメラを原点に固定して、方向を見ていることです$45^\circ$







$$→ Z +、前の章で導出された投影方程式を変更なしですぐに使用できます。カメラ座標系はカメラ空間と呼ばれます。カメラには、移動と回転で構成される変換もあると想定しています（スケールは省略します）。カメラの視点からシーンをレンダリングするには、シーン内の各頂点に逆変換を適用する必要があります。$\vec{Z_+}$

 V1 = V - camera.translation V2 = V1 * inverse(camera.rotation) V3 = perspective_projection(V2)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

変換マトリックス

一歩後退して、トップに何が起こるかを把握しましょう $$キャンバス上の点に投影されるまでモデル空間で V$V$$$$(cx, cy)$ 。



まず、モデル変換を適用して、モデル空間からワールド空間に移動します。

 V1 = V * instance.rotation V2 = V1 * instance.scale V3 = V2 + instance.translation
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、カメラ変換を適用して、ワールド空間からカメラ空間に移動します。

 V4 = V3 - camera.translation V5 = V4 * inverse(camera.rotation)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、遠近法の方程式を適用します。

 vx = V5.x * d / V5.z vy = V5.y * d / V5.z
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最後に、ビューポートの座標をキャンバスの座標にバインドします。

 cx = vx * cw / vw cy = vy * ch / vh
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ご覧のとおり、これはかなり大量の計算であり、各頂点について、多くの中間値が計算されます。これをすべて単一のマトリックス製品に減らすと便利ではないでしょうか？$$V、行列を掛けて直接取得$V$$$$cx$ と $$$cy$ ？



頂点を受け取り、変換された頂点を返す関数として変換を表現しましょう。 させる $$$C_T$ そして $$C Rはカメラの動きと回転になり、$C_R$$$$I_R$ 、 $$$I_S$ そして $$I T-インスタンスの回転、スケール、移動、$I_T$$$P-透視投影、および$P$$$M-ビューポートをキャンバスに配置します。$M$もし $$Vは元の頂点であり、$V$$$V ′はキャンバス上の点であるため、上記の方程式はすべて次のように表現できます。$V'$

$$

$$V' = M(P(C_R^{-1}(C_T^{-1}(I_T(I_S(I_R(V)))))))$$

理想的には、一連のソース変換と同じことを行うが、はるかに単純な式を持つ単一の変換が必要です。

$$

$$F = M \cdot P \cdot C_R^{-1} \cdot C_T^{-1} \cdot I_T \cdot I_S \cdot I_R$$

$$

$$V' = F(V)$$

表す単一の行列を見つける $$Fは重要なタスクです。主な問題は、変換がさまざまな方法で表現されることです。変位はポイントとベクトルの合計であり、回転とスケールは3x3ポイントとマトリックスの積であり、分割は透視投影で使用されます。しかし、すべての変換を1つの方法で表現でき、このメソッドに変換を作成するためのシンプルなメカニズムがある場合、必要なものが得られます。$F$

同次座標

表現を考えます $$$A = (1, 2, 3)$ 。 $$Aは、3D点または3D-ベクトルのですか？余分なコンテキストなしで見つける方法はありません。しかし、次の配置を取りましょう：ビューに4番目のコンポーネントを追加します。$A$



$$$w$ 。 もし $$w = 0、それからベクトルについて話している。$w = 0$もし $$w = 1、それからポイントについて話している。それがポイントです$w = 1$$$明確のように表さ$A$$$A = （1 、2 、3 、1 ）とベクトル$A = (1, 2, 3, 1)$$$→ Aは$\vec{A}$$$$(1, 2, 3, 0)$ 。点とベクトルには一般的な考え方があるため、これは同次座標と呼ばれます（注：同次座標は、より深くより詳細な幾何学的解釈を持ちますが、記事の主題とは関係ありません。ここでは、特定のプロパティを持つ便利なツールとして使用します）。



このような表現には、大きな幾何学的な意味があります。たとえば、2つのポイントを減算すると、ベクトルになります。

$$

$$(8, 4, 2, 1) - (3, 2, 1, 1) = (5, 2, 1, 0)$$

2つのベクトルを追加すると、ベクトルになります。

$$

$$(0, 0, 1, 0) + (1, 0, 0, 0) = (1, 0, 1, 0)$$

同様に、ポイントとベクトルを合計すると、ポイントが得られ、ベクトルにスカラーを乗算するとベクトルが得られるなどのことが簡単にわかります。



そして、座標は何ですか$$Wの、任意に等しくありません$w$$$0も$0$$$$1$ ？また、ポイントを表します。実際、3Dの任意のポイントには、一定の座標で無限の数の表現があります。座標と値の関係は重要です$$$w$ ; それは $$$(1, 2, 3, 1)$ そして $$（2 、4 、6 、2 ）同じ点を表します$(2, 4, 6, 2)$$$$(-3, -6, -9, -3)$ 。



これらすべての表現のうち、表現に名前を付けることができます $$w = 1は、同次座標の点の正準表現によります。他の表現からその標準表現またはデカルト座標への変換は簡単な作業です。$w = 1$

$$

$$\begin{pmatrix} x \\ y \\ z \\ w \end{pmatrix} = \begin{pmatrix}{c} x \over w \\ y \over w \\ z \over w \\ 1 \end{pmatrix} = \begin{pmatrix} x \over w \\ y \over w \\ z \over w \end{pmatrix}$$

つまり、デカルト座標を同次座標に変換したり、その逆をデカルト座標に変換したりできます。しかし、これはすべての変換の共通のビューを見つけるのにどのように役立ちますか？

同次回転行列

回転行列から始めましょう。同次座標でのデカルト回転行列3x3の表現は簡単です。座標以来$$wポイントは変更しないでください。右側に列、下部に行を追加し、それらをゼロで埋めて右下の要素に配置します。$w$$$値を保存するには 1$1$$$$w$ ：

$$

$$\begin{pmatrix} A & B & C \\ D & E & F \\ G & H & I \end{pmatrix} . \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x' \\ y' \\ z' \end{pmatrix} \rightarrow \begin{pmatrix} A & B & C & 0 \\ D & E & F & 0 \\ G & H & I & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} . \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x' \\ y' \\ z' \\ 1 \end{pmatrix}$$

スケーリング行列も均一な座標では自明であり、回転行列と同じ方法で作成されます。

$$

$$\begin{pmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & S_z \end{pmatrix} . \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x \cdot S_x \\ y \cdot S_y \\ z \cdot S_z \end{pmatrix} \rightarrow \begin{pmatrix} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} . \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x \cdot S_x \\ y \cdot S_y \\ z \cdot S_z \\ 1 \end{pmatrix}$$

均一な翻訳行列

前の例は単純でした。それらは既にデカルト座標の行列乗算として提示されていたので、追加するには十分でした$$座標を保存するには 1$1$$$$w$ 。しかし、追加としてデカルト座標で表した変位をどうしますか？



次のような4x4マトリックスが必要です。

$$

$$\begin{pmatrix} T_x \\ T_y \\ T_z \\ 0 \end{pmatrix} + \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} A & B & C & D \\ E & F & G & H \\ I & J & K & L \\ M & N & O & P \end{pmatrix} . \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + T_x \\ y + T_y \\ z + T_z \\ 1 \end{pmatrix}$$

最初に取得に焦点を当てましょう $$$x + T_x$ 。 この値は、マトリックスの最初の行にポイントを乗算した結果です。

$$

$$\begin{pmatrix} A & B & C & D \end{pmatrix} . \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = x + T_x$$

ベクトル積を開くと、

$$

$$Ax + By + Cz + D = x + T_x$$

そして、これから我々はそれを推測することができます $$$A = 1$ 、 $$$B = C = 0$ 、そして $$$D = T_x$ 。



同じ推論を残りの座標に適用して、変位について次の行列式を取得します。

$$

$$\begin{pmatrix} T_x \\ T_y \\ T_z \\ 0 \end{pmatrix} + \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \end{pmatrix} . \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + T_x \\ y + T_y \\ z + T_z \\ 1 \end{pmatrix}$$

和と積は、単純に和と積である行列とベクトルの積として表現できます。ただし、透視投影方程式では、$$$z$ 。それを表現するには？



で割ると考える誘惑があります$$zは、乗算するのと同じです$z$$$1 / z、これは実際に真実です。しかし、私たちの場合、座標は$1/z$$$特定のポイントの zは、各ポイントに適用される射影行列には含まれません。幸いなことに、同次座標での除算の場合が1つあります。座標による除算です$z$



$$デカルト座標への逆変換の w。そこで座標を変えることができます$w$$$座標への開始点の z$z$$$「投影された」点の w、それから投影された$w$$$$x$ そして $$ポイントをデカルト座標に変換した後の y：$y$

$$

$$\begin{pmatrix} A & B & C & D \\ E & F & G & H \\ I & J & K & L \end{pmatrix} . \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x.d \\ y.d \\ z \end{pmatrix} \rightarrow \begin{pmatrix} x.d \over z \\ y.d \over z \end{pmatrix}$$

この行列にはサイズがあることに注意してください $$$3\times 4$ ; それに4要素ベクトル（均一座標の変換された3D点）を掛けることにより、3要素ベクトル（同次座標の投影された2D点）を取得し、それを2次元のデカルト座標に変換する $$$w$ 。 これにより、正確な値が得られます。 $$$x'$ そして $$Y "、私たちは、探しています。ここでは十分ではありません$y'$



$$z ′、これは私たちが知っているように、定義により$z'$$$$d$ 。



翻訳行列の導出に使用したものと同様の推論を使用して、透視投影を次のように表現できます。

$$

$$\begin{pmatrix} d & 0 & 0 & 0 \\ 0 & d & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} . \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x.d \\ y.d \\ z \end{pmatrix} \rightarrow \begin{pmatrix} x.d \over z \\ y.d \over z \end{pmatrix}$$

キャンバス上のビューポートからの同次行列

最後のステップは、ビューポートに投影されたポイントをキャンバスに配置することです。それはただの二次元スケール変換です$$$S_x = c_w \over v_w$ そして $$$S_y = c_h \over v_h$ 。 つまり、マトリックスは次のようになります

$$

$$\begin{pmatrix} c_w \over v_w & 0 & 0 \\ 0 & c_w \over v_w & 0 \\ 0 & 0 & 1 \end{pmatrix} . \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x.c_w \over v_w \\ y.c_h \over v_h \\ z \end{pmatrix}$$

実際、投影マトリックスと組み合わせて、簡単な3Dからキャンバスへの変換マトリックスを取得するのは簡単です。

$$

$$\begin{pmatrix} d.cw \over vw & 0 & 0 & 0 \\ 0 & d.ch \over vh & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} . \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x.d.cw \over vw \\ y.d.cw \over vh \\ z \end{pmatrix} \rightarrow \begin{pmatrix} ({x.d \over z})({cw \over vw}) \\ ({y.d \over z})({ch \over vh}) \end{pmatrix}$$

実際的な理由から、射影行列は使用しません。代わりに、モデルとカメラの変換を使用し、次のように結果をデカルト座標に変換します。

$$

$$x' = {x.d.cw \over z.vw}$$

$$

$$y' = {y.d.ch \over z.vh}$$

これにより、マトリックス変換として表現できないポイントを投影する前に、他の3D操作を実行できます。

再び変換行列

以来、元の頂点の3D変換を表現できます $$Vは、4x4マトリックスとして投影する前に実行されます。これらの変換をすべて単純に1つの4x4マトリックスに結合し、乗算することができます。$V$

$$

$$F = C_R^{-1}.C_T^{-1}.I_T.I_S.I_R$$

そして、頂点変換は、次の製品を計算するだけの問題です。

$$

$$V' = F.V$$

さらに、変換を2つの部分に分解できます。

$$

$$M_{Camera} = C_R^{-1}.C_T^{-1}$$

$$

$$M_{Model} = I_T.I_S.I_R$$

$$

$$M = M_{Camera}.M_{Model}$$

これらのマトリックスは、頂点ごとに計算する必要はありません（これがマトリックスの使用のポイントです）。実際、すべてのフレームで計算する必要さえありません。



$$M C a m e r aはフレームごとに異なる場合があります。カメラの位置と向きに依存するため、カメラが移動または回転する場合は、カウントする必要があります。ただし、計算後は、フレームに描画された各オブジェクトに対して一定のままなので、フレームごとに最大1回計算されます。$M_{Camera}$



$$M M o d e lはモデルインスタンスの変換に依存するため、使用されるマトリックスはシーン内のオブジェクトに対して一度だけ変更されます。ただし、静止したオブジェクト（たとえば、木、建物）に対しては一定のままであるため、事前に計算してシーン自体に保存できます。移動オブジェクト（たとえば、レースゲームの車）の場合、移動するたびに（通常はすべてのフレームで）計算する必要があります。非常に高いレベルでは、シーンレンダリングの擬似コードは次のようになります。$M_{Model}$

 RenderModel(model, transform) { projected = [] for V in model.vertexes { projected.append(ProjectVertex(transform * V)) } for T in model.triangles { RenderTriangle(T, projected) } } RenderScene() { MCamera = MakeCameraMatrix(camera.position, camera.orientation) for I in scene.instances { M = MCamera*I.transform RenderModel(I.model, M) } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、さまざまなモデルの複数のインスタンスを含むシーンを描くことができます。おそらく移動や回転が可能で、シーンの周りでカメラを移動できます。







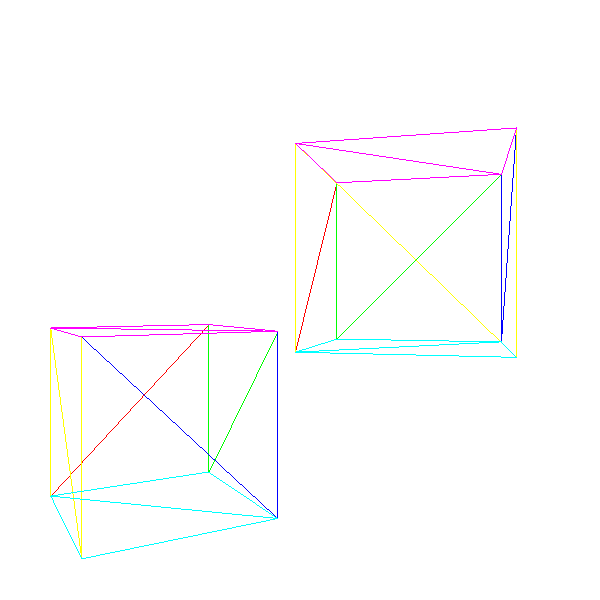
ソースコードと作業デモ>>



大きな一歩を踏み出しましたが、まだ2つの重要な制限があります。まず、カメラが動くと、オブジェクトがその背後にある可能性があり、あらゆる種類の問題が発生します。第二に、レンダリング結果はあまり良く見えません：まだワイヤフレームです。



次の章では、表示されるべきではないオブジェクトを扱い、残りの時間をレンダリングされたオブジェクトの外観の改善に費やします。

クリッピング

透視投影の章では、次の方程式を取得しました。

$$

$$P'_X = {P_X \cdot d \over P_Z}$$

$$

$$P'_Y = {P_Y \cdot d \over P_Z}$$

除算 $$P Zは問題を引き起こします。これにより、ゼロによる除算が発生する場合があります。また、正しく処理されていないカメラの後ろのポイントを表す負の値を生成することもあります。カメラの前にあるが非常に近いポイントでさえ、非常に歪んだオブジェクトの形で問題を引き起こす可能性があります。これらすべての問題を回避するために、投影面を超えて何もレンダリングしないことにしました$P_Z$



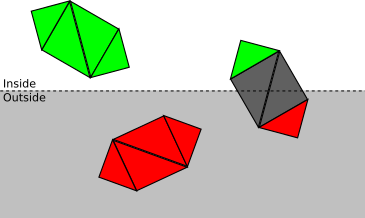
$$$Z = d$ 。このクリッピングプレーンを使用すると、すべてのポイントをクリッピングボリュームの内側または外側の ポイント、つまりカメラから実際に見えるスペースのサブセットに分割できます。この場合、カットオフの量は、 -それは" の前に半空間 $$Z = d "。クリッピングボリューム内にあるシーンの部分のみをレンダリングします。操作が少ないほど、レンダラーは高速になります。トップダウンアプローチを使用します。それぞれが4つのオブジェクトで構成されるシーンを考えます。三角形各段階で、この時点でクリッピングを停止できるかどうか、またはさらに詳細なクリッピングが必要かどうかをできる限り少なくするよう努めています。$Z = d$

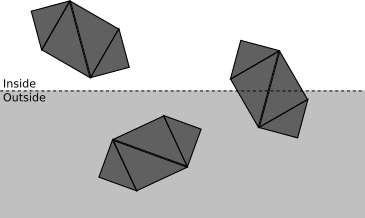
• オブジェクトが完全にクリッピングボリュームの内側にある場合、受け入れられます（緑色で強調表示されます）。それが完全に外側にある場合、破棄されます（赤）：

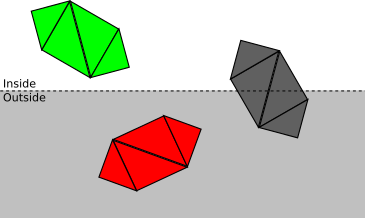
• それ以外の場合は、三角形ごとにプロセスを繰り返します。三角形が完全にカットオフボリュームの内側にある場合は受け入れられ、完全に外側の場合は破棄されます。

• そうでなければ、三角形自体を壊す必要があります。元の三角形は破棄され、1つまたは2つの三角形が追加され、カットオフボリューム内の三角形の部分が覆われます。

次に、プロセスの各段階を詳しく見ていきます。

クリッピングプレーンを設定する

最初にすることは、クリッピング平面方程式を見つけることです。何も悪いことはありません$$Z = dですが、これは私たちの目的にとって最も便利な形式ではありません。この章の後半で、他のクリッピングプレーンに対するより一般的なアプローチを開発するため、この特定のケースではなく一般的なアプローチを考え出す必要があります。3D平面の一般方程式の形式は$Z = d$



$$$Ax + By + Cz + D = 0$ 。 ポイントを意味する $$P = （x 、y 、z ）は、次の場合にのみ方程式を満たします。$P = (x, y, z)$$$Pは平面上にあります。式を次のように書き換えることができます。$P$$$$\langle \vec{N}, P \rangle + D = 0$ どこで $$$\vec{N} = (A, B, C)$ 。



ことに注意してください $$$\langle \vec{N}, P \rangle + D = 0$ それから $$K ⟨ → N、P ⟩ + K D = 0の任意の値の$k\langle \vec{N}, P \rangle + kD = 0$$$$k$ 。 特に、選択できます $$k = 1| → N | そして、新しい方程式を取得します$k = { 1 \over |\vec{N}| }$$$$\langle \vec{N}', P \rangle + D' = 0$ どこで $$$\vec{N}'$ 単位ベクトルです。 つまり、任意の与えられた平面に対して、単位ベクトルがあると仮定できます。 $$→ Nと実数$\vec{N}$$$そのような D$D$$$⟨ → N、P ⟩ + D = 0は、 この平面の方程式です。これは非常に便利な表現です。$\langle \vec{N}, P \rangle + D = 0\$



$$→ Nは実際には平面の法線であり、$\vec{N}$$$- D -平面の点に原点からの符号付き距離です。実際、どんな点でも$-D$$$$P$$$⟨ → N、P ⟩ + Dは、の符号からの距離であります$\langle \vec{N}, P \rangle + D$$$P平面に、わかりやすい$P$$$0は特別なケースです。$0$$$Pは平面上にあります。前に見たように、$P$



$$→ Nは次のように平面に垂直です$\vec{N}$$$→ - Nの、我々は選択したので、$\vec{-N}$$$→ Nは、カットオフボリュームの「内側」に向けられます。飛行機用$\vec{N}$$$Z = d通常を選択します$Z = d$$$（0 、0 、1 ）、そのカメラに対して"前方"ことを目的とします。ポイント以来$(0, 0, 1)$$$（0 、0 、D ）平面上の嘘、それは我々が知ることによって、それを計算することができ、平面の方程式を満たさなければなりません$(0, 0, d)$$$$D$ ：

$$

$$\langle \vec{N}, P \rangle + D = \langle (0, 0, 1), (0, 0, d) \rangle + D = d + D = 0$$

それは $$D = - D（注：あなたは些細からそれを得ることができます$D = -d$$$Z = d、次のように書き換えます$Z = d$$$$Z - d = 0$ 。 ただし、ここで説明する理由は、処理する他のすべての飛行機に適用され、これにより、 $$- Z + D = 0）も同様であるが、通常は、間違った方向に向けられています..$-Z + d = 0$

クリッピング量

カメラの後ろのオブジェクトがレンダリングされないことを保証できる単一のクリッピングプレーンを使用しますが、正しい結果が得られますが、これは完全に効果的ではありません。一部のオブジェクトはカメラの前にあるかもしれませんが、それでも見えません。たとえば、投影面の近くにあるが非常に右にあるオブジェクトの投影は、ビューポートからドロップアウトされるため、非表示になります。







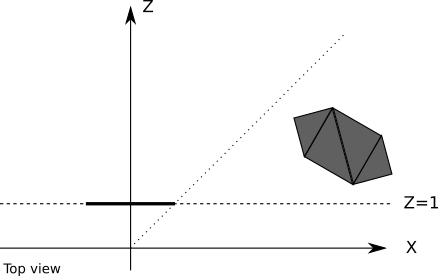
このようなオブジェクトの投影を計算するために使用するすべてのリソース、およびレンダリングするために作成された三角形と頂点の計算、無駄になります。このようなオブジェクトを完全に無視する方がはるかに便利です。



幸いなことに、これはまったく難しくありません。シーンを正確に切り取る追加の平面を指定できますビューポートから見えるものに。そのような平面はカメラとビューポートの両側で定義されます：







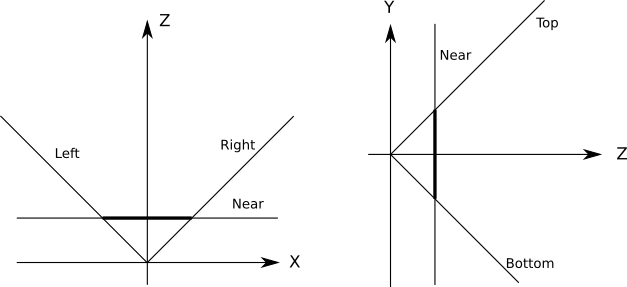
これらのすべての平面は$$D = 0（原点はすべての平面上にあるため）、したがって法線のみを決定できます。最も単純なケースはFOVです$D = 0$$$90 ∘面がでである時、$90^\circ$$$45 ∘、その正常なので、$45^\circ$$$（1√2、0、1√2）左面の場合、$({1 \over \sqrt{2}}, 0, {1 \over \sqrt{2}})$$$（- 1√2、0、1√2）正しい平面の場合、$({-1 \over \sqrt{2}}, 0, {1 \over \sqrt{2}})$$$（0 、1√2、1√2）底部および$(0, {1 \over \sqrt{2}}, {1 \over \sqrt{2}})$$$（0 、- 1√2、1√2）上部平面用。任意のFOVのクリッピング平面を計算するには、少数の三角法計算のみが必要です。カットオフのボリュームによってオブジェクトまたは三角形を切り取るには、各プレーンごとに順番にカットするだけで十分です。1つの平面で切断された後に「生き残った」すべてのオブジェクトは、残りの平面で切断されます。これは、クリッピングボリュームが各クリッピングプレーンによって定義される半空間の交差点であるため機能します。$(0, {-1 \over \sqrt{2}}, {1 \over \sqrt{2}})$

オブジェクト全体のクリッピング

クリッピングプレーンによってクリッピングボリュームを完全に設定したら、オブジェクトがこれらのプレーンのそれぞれによって定義された半空間の完全に内側か外側かを判断することから始めます。



各モデルを含むことができる最小の球の中に各モデルを配置するとします。この記事では、これをどのように行うかについては検討しません。球体は、複数のアルゴリズムのいずれかを使用して複数の頂点から計算できます。または、モデル設計者が近似値を指定できます。いずれにしても、我々はセンターを持っていると仮定します$$Cおよび半径$C$$$r球体、各オブジェクトを完全に含む：球体と平面の間の空間的関係を次のカテゴリに分割できます。$r$

• . ; ( ):

• . ; ( , — ):

• . , ; , , . .

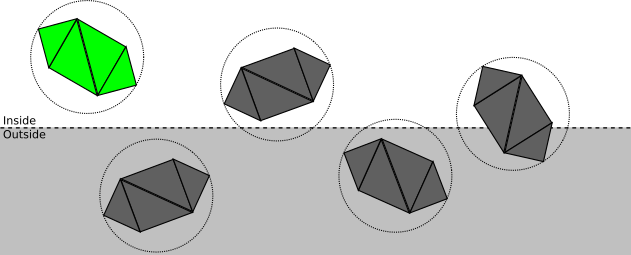
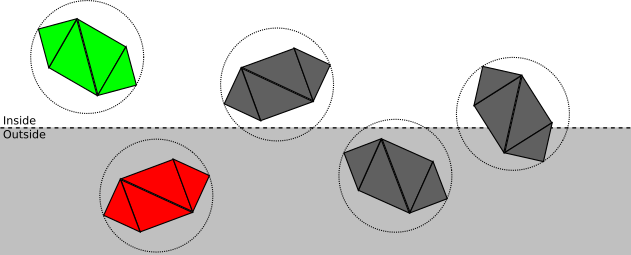
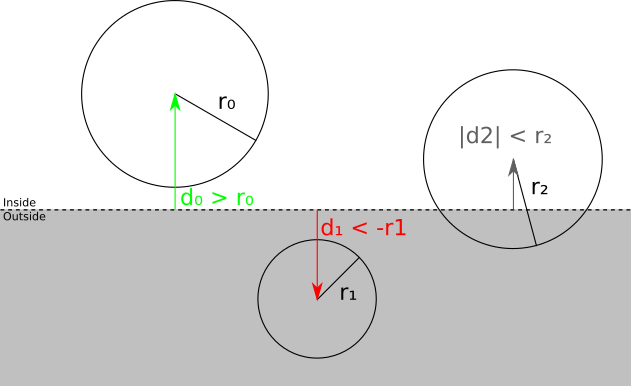
それでは、この分類は実際にどのように機能するのでしょうか？平面の方程式の任意の点を置き換えると、点から平面までの符号付きの距離が得られるように、クリッピング平面を表現する方法を選択しました。特に、記号で距離を計算できます$$d境界球の中心から平面まで。したがって$d$$$d > rの場合、球体は平面の前にあります。$d > r$もし $$D < - R、球、平面の後方に配置されています。そうでなければ$d < -r$$$d | < r、つまり、平面は球と交差します。$d| < r$

三角形のクリッピング

オブジェクトがクリッピングプレーンの完全に前にあるのか、完全に後ろにあるのかを判断するには、球面チェックでは不十分な場合は、それに対して各三角形を切り取る必要があります。



平面への符号との距離の符号をとることにより、クリッピング平面に関して三角形の各頂点を分類できます。距離がゼロまたは正の場合、頂点はクリッピングプレーンの前にあり、そうでない場合-後ろに







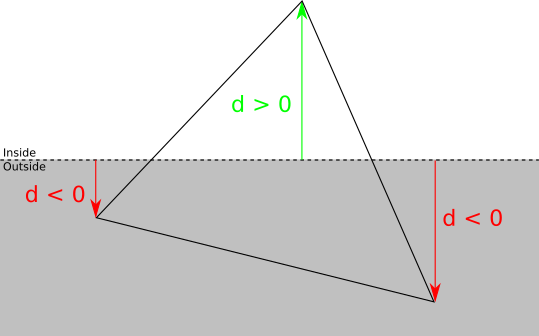
ある場合：考えられる4つのケースがあります。

• 3つのピークが平面の前にあります。この場合、三角形全体がクリッピングプレーンの前にあるため、このプレーンに関連するさらなるクリッピングなしで受け入れられます。
• . , .
• . させる $$$A$ — $$$ABC$ , . この場合 $$$ABC$ , $$$AB'C'$ どこで $$$B '$ そして $$$C'$ — $$$AB$ そして $$$AC$ .

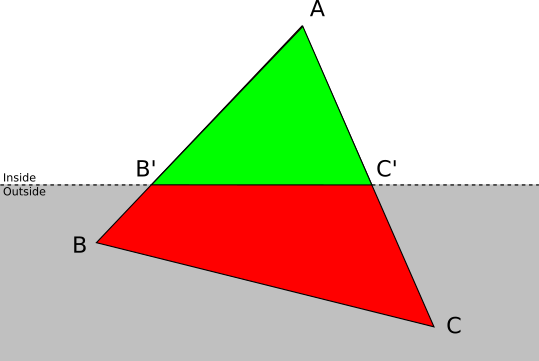
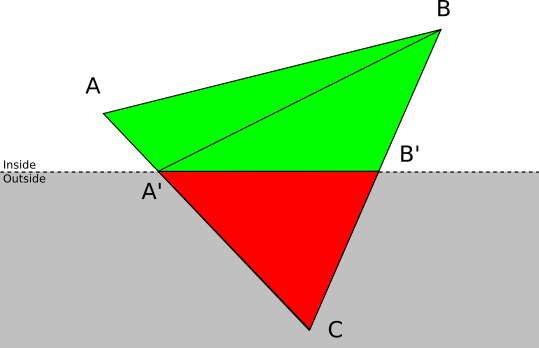
• . させる $$$A$ そして $$$B$ — $$$ABC$ , . ABC , : $$$ABA'$ そして $$$A'BB'$ どこで $$$A '$ そして $$$B '$ — $$$AC$ そして $$$BC$ .

各三角形のクリッピングを実行するには、三角形の辺とクリッピング平面の交点を計算する必要があります。交差点の座標を計算するだけでは不十分であることに注意してください：頂点に関連付けられた属性の対応する値、たとえば、「シェーディングされた三角形のレンダリング」の章で行ったシェーディング、または後続の章で説明されている属性の1つを計算する必要もあります。



方程式によって定義されたクリッピング平面があります$$$\langle N, P \rangle + D = 0$ 。 三角形の側面 $$A Bは、パラメトリック方程式を使用して次のように表現できます。$AB$$$$P = A + t(B - A)$ で $$$0 \le t \le 1$ 。 パラメータ値を計算するには $$交点が発生する tを置き換えます$t$$$平面の方程式の Pからセグメントのパラメトリック方程式へ：$P$

$$

$$\langle N, A + t(B - A) \rangle + D = 0$$

スカラー積の線形特性を使用して、以下を取得します。

$$

$$\langle N, A \rangle + t\langle N, B - A \rangle + D = 0$$

計算する $$$t$ ：

$$

$$t = {-D - \langle N, A \rangle \over \langle N, B - A \rangle}$$

ソリューションは常に存在することがわかっています $$A Bは平面を横切ります。$AB$数学的に $$⟨ Nは、B - A ⟩このセグメントひいてはセグメント平面が交差しないことを意味する、正常に直交することを意味するので、ゼロにすることはできません。コンピューティングにより$\langle N, B - A \rangle$



$$t、その交点を得る$t$$$Qはちょうど等しい$Q$

$$

$$Q = A + t(B - A)$$

に注意してください $$tはセグメントの一部です$t$$$交差点が発生したB。$AB$させる $$$\alpha_A$ そして $$α Bは、特定の属性の値であります$\alpha_B$$$ a l p h a at points$\ alpha$$$$A$ そして $$$B$ ; 属性がそれに沿って線形に変化すると仮定した場合 $$$AB$ それから $$α Qは、単にように計算することができます。$\alpha_Q$

$$

$$\alpha_Q = \alpha_A + t(\alpha_B - \alpha_A)$$

コンベヤーのクリッピング

章の順序は、レンダリングパイプラインで実行される操作の順序に対応していません。導入部で説明したように、章は、できるだけ早く明白な進歩を遂げられるように配置されています。



クリッピングは3D操作です。シーン内の2つの3Dオブジェクトを受け取り、シーン内の3Dオブジェクトの新しいセット、つまりシーンとクリッピングボリュームの交差点を生成します。オブジェクトがシーンに配置された後（つまり、モデルとカメラの変換後に頂点が使用された後）、透視投影の前にクリッピングを実行する必要があることは明らかです。



この章で説明する手法は確実に機能しますが、非常に一般的です。シーンについて事前に知れば知るほど、クリッピングはより効果的になります。たとえば、多くのゲームでは、可視性情報を追加してゲームカードを前処理します。シーンを「部屋」に分割することができれば、特定の各部屋から見える部屋をリストするテーブルを作成できます。将来シーンをレンダリングするときは、カメラがどの部屋にあるかを知る必要があります。その後、「不可視」とマークされたすべての部屋を無視して、レンダリング時にかなりのリソースを節約できます。もちろん、同時に前処理により多くの時間を費やす必要があり、シーンはより厳密に定義されます。

非表示の表面を削除する

あらゆる視点からあらゆるシーンをレンダリングできるようになったので、ワイヤーフレームグラフィックスを改善しましょう。



明らかな最初のステップは、ソリッドオブジェクトにソリッドな外観を与えることです。これを行うには、DrawFilledTriangle()



ランダムな色を使用して各三角形を描画し、何が起こるかを見てみましょう：







キューブにあまり似ていませんよね？



ここでの問題は、他の三角形の後ろにあるはずの三角形がそれらの前に描画されることです。なんで？というのも、モデルを設定するときに取得した順序で、ほぼランダムな順序でキャンバスに2D三角形を描くからです。



ただし、モデルの三角形を定義する場合、「正しい」順序はありません。モデルの三角形が並べ替えられて、最初に背面が描画され、次に前面と重なると仮定します。期待どおりの結果が得られます。ただし、キューブを$$180は∘、我々は逆の状況を取得する-長い三角形が近くに重なります。$180^\circ$

アーティストアルゴリズム

この問題の最初の解決策は、「アーティストアルゴリズム」として知られています。現実世界のアーティストは、最初に背景を描き、次にその一部を前面のオブジェクトで覆います。シーンの各三角形を取得し、モデルとカメラの変換を適用し、それらを前後に並べ替え、その順序で描画することで、同じ効果を実現できます。



三角形は正しい順序で描画されますが、このアルゴリズムには欠点があり、実用的ではありません。



第一に、非常にうまくスケーリングしません。最適なソートアルゴリズムには速度があります$$O （N 。L O G （N ）） \）、すなわち、より三角形の数を2倍にすることによって倍の実行時間。つまり、小さなシーンでも機能しますが、シーンの複雑さが増すとすぐにボトルネックになります。第二に、三角形のリスト全体の同時知識が必要です。これには大量のメモリが必要であり、レンダリングにストリーミングアプローチを使用することはできません。モデルの三角形が一方の端から入り、ピクセルがもう一方の端から出るパイプラインとしてレンダリングを認識する場合、各三角形が処理されるまでピクセルの表示を開始することは不可能です。これは、このアルゴリズムを並列化できないことを意味します。$O(n.log(n))$







第三に、これらの制限に耐えても、三角形の正しい順序が存在しない場合があります。次の場合を考えてみましょう。







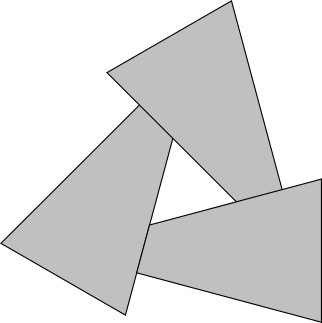
これらの三角形を描画する順序は関係ありません- 常に間違った結果が得られます。

深度バッファ

三角形のレベルでの問題の解決策が機能しない場合、ピクセルレベルでの解決策は確実に機能し、同時にアーティストのアルゴリズムのすべての制限を克服します。



基本的に、キャンバスの各ピクセルを「正しい」色でペイントします。この場合、「正しい」色はカメラに最も近いオブジェクトの色です（この場合$$$P_1$ ）：







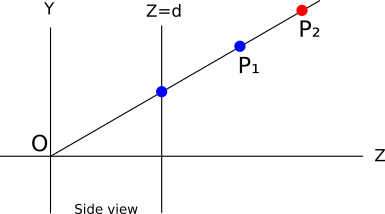
これは簡単にできることがわかりました。値を保存するとします$$キャンバスの各ピクセルで現在表されている Zポイント。特定の色でピクセルをペイントするかどうかを決定するときは、座標が$Z$$$ペイントする Zポイント、座標が少ない$Z$$$既に存在する Zポイント。最初に塗りつぶしたい三角形の順序を想像してください$Z$



$$P 2その後$P_2$$$$P_1$ 。 ピクセルは赤く塗られ、その $$Zはとしてマークされています$Z$$$$Z_{P_2}$ 。 それから塗り直します $$P 1および$P_1$$$Z P 2 > Z P 1の場合、ピクセルは青で上書きされます。正しい結果が得られます。もちろん、値に関係なく正しい結果が得られました$Z_{P_2} > Z_{P_1}$



$$$Z$ 。 最初に塗り直したい場合 $$P 1その後$P_1$$$$P_2$ ？ ピクセルは最初に青に変わり、 $$Z P 1が保存されています。しかし、その後、私たちは塗りつぶしたいです$Z_{P_1}$$$P 2および$P_2$$$Z P 2 > Z P 1の場合、ペイントしません（これを行うと、リモートポイントをペイントし、近い方のポイントを閉じます）。再び青いピクセルが得られますが、これは正しい結果です。実装に関しては、座標を保存するためのバッファが必要です$Z_{P_2} > Z_{P_1}$



$$キャンバス上の各ピクセルの Z。これは深度バッファーと呼ばれ、そのサイズはキャンバスのサイズと自然に等しくなります。しかし、意味はどこから来るのですか$Z$



$$$Z$ ？



値でなければなりません。 $$変換後、透視投影前の Zポイント。そのため、シーンのセットアップの章では、最終結果に含まれるような変換行列を設定します$Z$$$$1/Z$ 。



したがって、値を取得できます $$これらの値の Z$Z$$$$1/Z$ 。ただし、この値はピークに対してのみあります。ピクセルごとに取得する必要があります。



これは、属性割り当てアルゴリズムを適用する別の方法です。使用しない理由$$Zを属性として、三角形のエッジに沿って補間しませんか？手順はすでに知っています。我々は、値を取る、および、計算、およびそれらから得、そしてその後、計算の各水平ラインの各画素について。そして、盲目的に行う代わりに、次のことを行います。$Z$Z0



Z1



Z2



Z01



Z02



Z02



z_left



z_right



z_segment



PutPixel(x, y, color)

 z = z_segment[x - xl] if (z < depth_buffer[x][y]) { canvas.PutPixel(x, y, color) depth_buffer[x][y] = z }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これが機能するには、depth_buffer



値で初期化する必要があります$$+ ∞（または単に「非常に大きな値」）。結果ははるかに良くなりました：ソースコードと動作デモ>>$+\infty$

なぜZではなく1 / Z

しかし、話はこれで終わりではありません。 値 $$頂点の Zは正しい（最終的にはデータから取得されます）が、ほとんどの場合、線形補間された値$Z$$$残りのピクセルの Zは無効になります。この近似は深さをバッファするのに「十分」ですが、将来的には干渉します。値がどれほど正しくないかを確認するには、次の直線の単純なケースを考えます。$Z$



$$$A (-1, 0, 2)$ で $$$B (1, 0, 10)$ 。 中間セクション $$Mには座標があります$M$$$$(0, 0, 6)$ ：







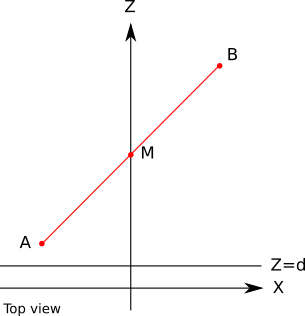
これらの点の投影を計算してみましょう $$$d = 1$ 。 $$$A'_x = A_x / A_z = -1 / 2 = -0.5$ 。 同様に $$$B'_x = 0.1$ そして $$$M'_x = 0$ ：







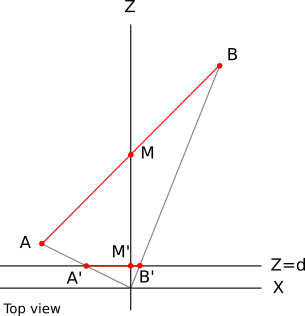
値を線形補間するとどうなりますか $$$A_z$ そして $$計算値を取得する B z$B_z$$$$M_z$ ？線形関数は次のようになります。







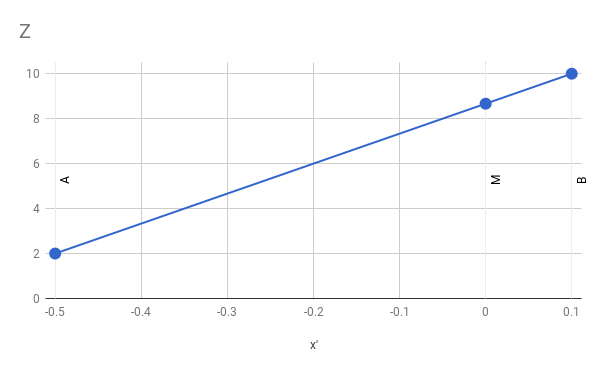
これから、次のように結論付けることができます。

$$

$${ M_z - A_z \over M'_x - A'_x } = { B_z - A_z \over B'_x - A'_x }$$

$$

$$M_z = A_z + (M'_x - A'_x) ({B_z - A_z \over B'_x - A'_x})$$

数値を代入して算術計算を実行すると、次のようになります

$$

$$M_z = 2 + (0 - (-0.5))({10 - 2 \over 0.1 - (-0.5)}) = 2 + (0.5)({8 \over 0.6}) = 8.666$$

明らかに等しくない$$$M_z = 6$ 。



それで問題は何ですか？属性の割り当てを使用しますが、これはうまく機能することがわかっています。データから取得した正しい値を彼に提供します。なぜ結果が間違っているのですか？



問題は、線形補間を行うときに暗黙的に意味することです。補間する関数は線形です。そして、私たちの場合、これはそうではありません！



もし $$Z = F （X ' Yが'）線形関数であろう$Z = f(x', y')$$$$x'$ そして $$y ′、次のように書くことができます。$y'$$$Z = A ⋅ X ' + B ⋅ Y ' + C幾つかの値について$Z = A \cdot x' + B \cdot y' + C$$$$A$ 、 $$$B$ そして $$$C$ 。このタイプの関数には、次のプロパティがあります。2つのポイント間の値の差は、ポイント自体ではなく、ポイント間の差に依存します。

$$

$$f(x' + \Delta x, y' + \Delta y) - f(x', y') = [A (x' + \Delta x) + B (y' + \Delta y) + C] - [A \cdot x' + B \cdot y' + C]$$

$$

$$= A (x' + \Delta x - x') + B (y' + \Delta y - y') + C - C$$

$$

$$= A \Delta x + B \Delta y$$

つまり、画面座標の所定の差に対して、その差は $$Zは常に同じです。より正式には、調査中の三角形を含む平面の方程式は、$Z$

$$

$$AX + BY + CZ + D = 0$$

一方、透視投影方程式があります：

$$

$$x' = {Xd \over Z}$$

$$

$$y' = {Yd \over Z}$$

再び入手できます $$$X$ そして $$$Y$ ：

$$

$$X = {Zx' \over d}$$

$$

$$Y = {Zy' \over d}$$

交換する場合 $$$X$ そして $$これらの式を持つ平面方程式の Y、$Y$

$$

$${Ax'Z + By'Z \over d} + CZ + D = 0$$

掛け算 $$dおよび表現$d$$$Z、我々は得る$Z$

$$

$$Ax'Z + By'Z + dCZ + dD = 0$$

$$

$$(Ax' + By' + dC)Z + dD = 0$$

$$

$$Z = {-dD \over Ax' + By' + dC}$$

明らかに線形関数ではないもの$$$x'$ そして $$$y'$ 。



ただし、計算する場合 $$1 / Z、その後取得$1/Z$

$$

$$1/Z = {Ax' + By' + dC \over -dD}$$

これは明らかに次の線形関数です$$$x'$ そして $$$y'$ 。



これが実際に機能することを示すために、上記の例を示しますが、今回は線形補間を使用して計算します $$$1/Z$ ：

$$

$${ M_{1 \over z} - A_{1 \over z} \over M'_x - A'_x } = { B_{1 \over z} - A_{1 \over z} \over B'_x - A'_x }$$

$$

$$M_{1 \over z} = A_{1 \over z} + (M'_x - A'_x) ({B_{1 \over z} - A_{1 \over z} \over B'_x - A'_x})$$

$$

$$M_{1 \over z} = {1 \over 2} + (0 - (-0.5)) ({{1 \over 10} - {1 \over 2} \over 0.1 - (-0.5)}) = 0.166666$$

したがって、

$$

$$M_z = {1 \over M_{1 \over z}} = {1 \over 0.166666} = 6$$

これは実際には正しい値です。



これはすべて、深さをバッファリングするために、値の代わりに$$Z使用値$Z$$$$1/Z$ 。 擬似コードの唯一の実際的な違いは、バッファを値で初期化する必要があることです $$$0$ （つまり $$1+ ∞）、比較を逆さまにする必要があります（より高い値を維持してください）$1 \over + \infty$$$低い値に対応する 1 / Z$1/Z$$$$Z$ ）

バックエッジのクリッピング

深度バッファリングにより、望ましい結果が得られます。しかし、より速く同じことをすることはできますか？



キューブに戻る：結果として各ピクセルが正しい色になったとしても、それらのいくつかは何度も何度も再描画されます。たとえば、立方体の背面が前面にレンダリングされる場合、多くのピクセルが2回塗りつぶされます。各ピクセルに対して実行される操作の数の増加に伴い（現時点では、各ピクセルに対してのみ計算します$$1 / Zですが、たとえば、すぐに照明を追加します）、決して表示されないピクセルの計算はますます高価になります。これらの計算をすべて行う前に、事前にピクセルをドロップできますか？描画を開始する前でも三角形全体を破棄できることがわかりました！ここまで、前面と背面について非公式に話しました。各三角形に2つの辺があることを想像してください。同時に、三角形の片側しか見ることができません。これらの2つの側面を分離するには、各三角形にその表面に垂直な矢印を追加します。次に、立方体を取り出し、各矢印が外側を向いていることを確認します。$1/Z$















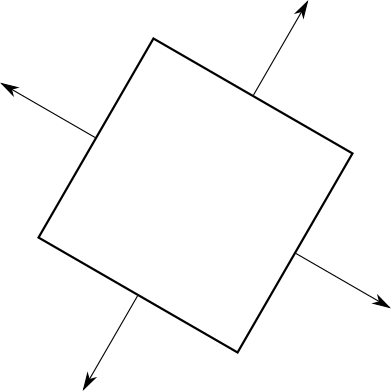
これで、この矢印を使用して、各三角形がカメラに向かっているのか、カメラから離れているのかに応じて、「正面」と「背面」に分類できます。より正式な場合、表示ベクトルとこの矢印（実際には三角形の法線ベクトル）が対応してより小さいまたは大きい角度を形成する場合$$$90^\circ$ ：







一方、同じ向きの両側三角形があるため、閉じたオブジェクトの「内側」と「外側」を指定できます。定義上、閉じたオブジェクトの内部部分は表示されません。これは、閉じたオブジェクトの場合、カメラの位置に関係なく、前面が背面と完全に重なり合うことを意味します。



これは、フロントエッジによって再描画されるため、エッジをまったく描画する必要がないことを意味します。

三角形の分類

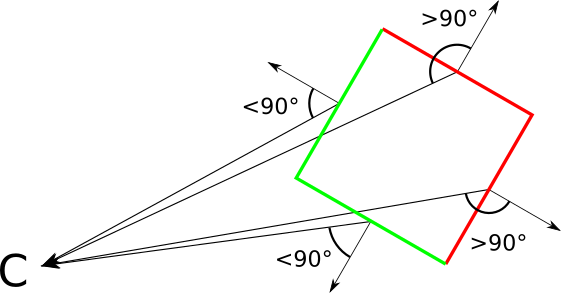
これを形式化して実装しましょう。三角形の法線ベクトルがあるとしましょう$$→ Nおよびベクトル$\vec{N}$$$→三角形の頂点からカメラへの V。$\vec{V}$させる $$→ Nは、被写体の外側方向を示します。三角形を前面または背面として分類するには、間の角度を計算します$\vec{N}$$$$\vec{N}$ そして $$→ V、その後、それらが$\vec{V}$$$90 ∘互いに対して。スカラー積のプロパティを使用して、これをさらに簡素化できます。を示す場合、それを忘れないでください$90^\circ$



$$ a l p h間の角度$\ alpha$$$$\vec{N}$ そして $$$\vec{V}$ それから

$$

$${{\langle \vec{N}, \vec{V} \rangle} \over {|\vec{N}||\vec{V}|}} = cos(\alpha)$$

以来 $$c o s （α ）は以下に対して負ではありません$cos(\alpha)$$$| α | ≤ 90 ∘、前面または背面の両方のエッジを分類するために、それだけでその符号を知ることで十分です。それは注目に値する$|\alpha| \le 90^\circ$$$$|\vec{N}|$ そして $$| → V | 常に正であるため、表現のサインに影響を与えません。だから$|\vec{V}|$

$$

$$sign(\langle \vec{N}, \vec{V} \rangle) = sign(cos(\alpha))$$

つまり、分類は非常に簡単です。

$$$\langle \vec{N}, \vec{V} \rangle \le 0$	背面
$$$\langle \vec{N}, \vec{V} \rangle > 0$	前面

ボーダーケース $$⟨ → N、→ V ⟩ = 0であり、我々は三角形のエッジを見た場合に相当する、ときにカメラ三角形同一平面（同一平面）。どのように分類してもかまいませんが、これは結果に大きな影響を与えないため、退化した三角形の処理を避けるために、裏面として分類することにしました。法線ベクトルはどこで取得しますか？ベクトル演算-ベクトル積があることがわかります$\langle \vec{N}, \vec{V} \rangle = 0$



$$→ A × → B、2つのベクトルを受け取る$\vec{A} \times \vec{B}$$$$\vec{A}$ そして $$→ B、およびそれらに垂直なベクトルになります。頂点を互いに減算することにより、つまり三角形の法線ベクトルの方向を計算することにより、三角形と同一平面上の2つのベクトルを簡単に取得できます。$\vec{B}$$$A B Cは簡単な操作です：$ABC$

$$

$$\vec{V_1} = B - A$$

$$

$$\vec{V_2} = C - A$$

$$

$$\vec{P} = \vec{V_1} \times \vec{V_2}$$

「法線ベクトル」ではなく、「法線ベクトルの方向」と言ったことに注意してください。これには2つの理由があります。最初は$$| → P | 必ずしも等しくない$|\vec{P}|$$$$1$ 。 正規化はそれほど重要ではありません $$→ Pは簡単な操作になります。$\vec{P}$$$$\langle \vec{N}, \vec{V} \rangle$ 。



しかし、2番目の理由は、 $$→ Nは法線ベクトルです$\vec{N}$$$A B C、その後も$ABC$$$$\vec{-N}$ ！



もちろん、この場合、どの方向に向かうかは非常に重要です $$→ N。これにより、三角形を前面または背面に分類できるためです。ベクトル積は可換ではありません。特に$\vec{N}$$$$\vec{A} \times \vec{B} = -\vec{B} \times \vec{A}$ 。これは、法線が「in」または「out」を示すかどうかを決定するため、単純に任意の順序で三角形の頂点を減算できないことを意味します。



ベクトル積は可換ではありませんが、当然偶然ではありません。



常に使用した座標系（Xを右、Yを上、Zを前）は左手と呼ばれます。これは、左手の親指、人差し指、中指をこれらの方向に向けることができるためです（親指を上に、インデックスを前に、中右）。右手座標系はそれに似ていますが、右手の人差し指は左を指しています。

シェーディング

シーンに「リアリズム」を追加していきましょう。この章では、シーンに光源を追加する方法と、シーンに含まれるオブジェクトを照らす方法を学習します。



この章は、ライティングではなくシェーディングと呼ばれます。これらは密接に関連する2つの概念ですが、異なる概念です。照明とは、シーンの1つのポイントに対する照明の効果を計算するために必要な数学とアルゴリズムを指します。シェーディングでは、テクニックを使用して、光源の効果を個別のポイントセットからオブジェクト全体に伝播します。章ライティングセクションレイトレーシング



照明について知っておくべきことはすべてお伝えしました。環境照明、スポット照明、指向性照明を指定できます。与えられた位置でのシーン内の任意のポイントの照明とこのポイントでの表面法線の計算は、レイトレーサーとラスタライザーで同じ方法で実行されます。理論はまったく同じです。



この章で学習するより興味深い部分は、この「点の光」をどのように取り、三角形で構成されるオブジェクトに対して機能させるかです。

フラットシェーディング

シンプルから始めましょう。点の照明を計算できるので、三角形の任意の点（中心など）を選択し、そこで照明を計算し、照明値を使用して三角形全体をシェーディングします（実際のシェーディングを実行するには、三角形の色に照明値を掛けます）：







そうではありませんあまりにも悪い。そして、それが起こった理由を見るのは非常に簡単です。三角形の各ポイントは同じ法線を持ち、光源が十分に遠い間、ライトベクトルはほぼ平行です。つまり、各ポイントはほぼ同じ量の照明を受け取ります。これは、キューブの各辺を構成する2つの三角形の違いを大まかに説明しています。



しかし、各ポイントが独自の法線を持つオブジェクトを取得するとどうなりますか？







あまり良くない。オブジェクトが実際の球体ではなく、平面三角形の破片で構成される近似であることは非常に明白です。このタイプの照明は、湾曲したオブジェクトをフラットに見せるため、フラットシェーディングと呼ばれます。

グーローシェーディング

どのように写真を改善しますか？ほぼすべてのツールをすでに持っている最も簡単な方法は、三角形の中心ではなく、3つの頂点の照明を計算することです。これらの照明値$$$0.0$ 前に $$1.0は最初にエッジに沿って線形補間され、次に三角形の表面に沿って線形補間され、各ピクセルが滑らかに変化する色相で塗りつぶされます。つまり、実際、これはシェーディングされた三角形のレンダリングの章で行ったこととまったく同じです。唯一の違いは、固定値を割り当てるのではなく、照明モデルを使用して各頂点の輝度値を計算することです。これはアンリ・ゴウロによるグーローシェーディングと呼ばれ、1971年にこのアイデアを思いつきました。これを立方体と球体に適用した結果は次のとおりです。立方体は少し良く見えます。これは、各辺の両方の三角形に2つの共通の頂点があり、もちろん両方の照明がまったく同じように計算されるためです。$1.0$















ただし、球体はまだファセットに見え、その表面の不均一性は非常に不規則に見えます。結局、球面を一連の平面として扱うため、これは驚くべきことではありません。特に、隣接する面に非常に異なる法線を使用します。特に、異なる三角形の非常に異なる法線を使用して同じ頂点の照明を計算します。







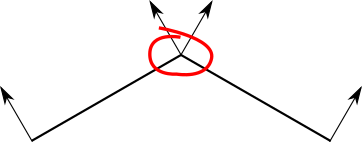
一歩後退しましょう。平らな三角形を使用して湾曲したオブジェクトを表すという事実により、テクニックは制限されますが、オブジェクト自体のプロパティは制限されません。



球体モデルの各頂点は球体の点に対応しますが、それらが定義する三角形は球体の表面の単純な近似です。したがって、頂点が球体のポイントをできるだけ正確に表すと便利です。これは、とりわけ、球体の実際の法線を使用する必要があることを意味します。







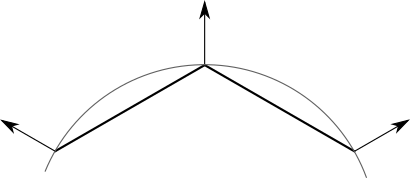
ただし、これは立方体には適用されません。三角形の頂点位置は共通ですが、各面は他の面とは独立してシェーディングする必要があります。立方体の頂点には、単一の「真の」法線がありません。



このジレンマを解決するには？思ったより簡単です。三角形の法線を計算する代わりに、三角形をモデルの一部にします。したがって、オブジェクトの開発者は法線を使用して、表面の曲率（またはその不在）を記述することができます。また、立方体や平らな面を持つ他の表面の場合を考慮するために、頂点の法線を、頂点自体ではなく、三角形の頂点のプロパティにします。

 model { name = cube vertexes { 0 = (-1, -1, -1) 1 = (-1, -1, 1) 2 = (-1, 1, 1) ... } triangles { 0 = { vertexes = [0, 1, 2] normals = [(-1, 0, 0), (-1, 0, 0), (-1, 0, 0)] } ... } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これは、対応する頂点法線でグーローシェーディングを使用してレンダリングされたシーンです。







立方体は依然として立方体のように見え、球体は球体のように見えます。実際、その外形を見ると、三角形で構成されていることがわかります（この問題は、より小さな三角形を使用し、処理能力を増やすことで解決できます）。



ただし、光沢のあるオブジェクトをレンダリングしようとすると、錯覚は破壊されます。球上のフレアは驚くほど非現実的です。



ここには小さな問題があります。点光源を大きな顔に非常に近づけると、自然に明るく見えるようになり、鏡の効果がより顕著になります。ただし、正反対の画像が得られます。







ここで何が起こるか：三角形の中心近くのドットがより明るくなると予想されますが（ $$$\vec{L}$ そして $$→ Nはほぼ平行です）、これらの点ではなく頂点で照明を計算し、光源が表面に近づくほど、法線との角度が大きくなります。これは、各内部ピクセルが2つの低い値の間で補間された輝度を使用することを意味します。つまり、それらも低い値を持ちます。$\vec{N}$

フォンシェード

Guroのシェーディング制限は簡単に克服できますが、通常どおり、品質とリソースの間にはトレードオフがあります。



フラットシェーディングでは、三角形ごとに1つの計算が使用されました。グーローシェーディングでは、三角形ごとに3つの照明の計算と、三角形上の単一の属性（光）の補間が必要でした。この品質とピクセルあたりのコストの向上における次のステップは、三角形の各ピクセルの照明を計算することです。



これは、理論的には特に複雑ではないようです。最後に、3つのポイントの照明を既に計算し、レイトレーサーのピクセルごとの照明を計算しました。しかし、ここでのコツは、照明方程式の入力データがどこから来たかを見つけることです。



必要です $$$\vec{L}$ 。 指向性光源を使用 $$→ Lが与えられます。点光源の場合$\vec{L}$$$→ Lはシーン内のポイントからのベクトルとして与えられます$\vec{L}$$$Pから光源の位置$P$$$$Q$ 。 しかし、私たちは持っていません $$三角形の各ピクセルの Q。ただし、頂点のみ。プロジェクションがあります$Q$



$$P-すなわち$P$$$$x'$ そして $$y ´キャンバスに描画します！私たちはそれを知っています$y'$

$$

$$x' = {Xd \over Z}$$

$$

$$y' = {Yd \over Z}$$

また、補間されたが幾何学的に正しい値があります $$1深度バッファリングアルゴリズムの一部としての Z$1 \over Z$

$$

$$x' = Xd{1 \over Z}$$

$$

$$y' = Yd{1 \over Z}$$

したがって、これらの値から取得できます $$$P$ ：

$$

$$X = {x' \over d{1 \over Z}}$$

$$

$$Y = {y' \over d{1 \over Z}}$$

$$

$$Z = {1 \over {1 \over Z}}$$

必要です $$$\vec{V}$ 。 これは簡単なことです $$Pは、カメラの位置がわかっているため、上で説明したとおりです。必要です$P$



$$$\vec{N}$ 。私たちはまだ頂点にのみ法線を持っています。ハンマーを手に持っているとき、すべてのタスクは釘のようなもので、ハンマーは属性値の線形補間です！値を取ることができます$$$N_x$ 、 $$$N_y$ そして $$各頂点で N zであり、線形補間できる無関係な実数として認識します。各ピクセルで、補間されたコンポーネントをベクトルに再構築し、正規化し、このピクセルの法線として使用します。この手法は、1973年に発明したBui Tien Phongという名前でPhongシェーディングと呼ばれています。その結果は次のとおりです：ソースコードと作業デモ>>球体は輪郭を除いて素晴らしく見えます（ただし、シェーディングアルゴリズムはこれを責めるものではありません）。また、三角形に光源を近づけたときの効果は期待どおりに動作します。また、ソースにエッジを近づけるという問題も解決し、期待どおりの結果が得られます。$N_z$



























この段階で、シャドウと反射を除き、最初の部分で開発されたレイトレーサーの機能に既に到達しています。同じシーンを使用する場合に開発しているラスタライザの出力は次のとおりです。







また、参照用にレイトレーシングを使用したバージョン







もあります。まったく異なるテクノロジを使用しているにもかかわらず、ほとんど同じように見えます。 1つのシーンをレンダリングするためにさまざまな手法を使用したため、これは論理的です。唯一の顕著な違いは、球体のエッジです。これは、レイトレーサーが数学的に完全な球体としてレンダリングし、ラスタライザーは多くの三角形を近似します。

テクスチャー

今のところ、立方体や球体などのオブジェクトをレンダリングし、ライティングでそれらに影響を与えることができます。ただし、通常は、キューブや球ではなく、ボックスや惑星、ゲーム用サイコロ、大理石をレンダリングする必要があります。



木箱を考えてみましょう。キューブを木製の箱に変える方法は？ 1つのオプションは、ツリーの構造、釘の頭などを作成する多数の三角形を追加することです。これは機能しますが、シーンの幾何学的な複雑さのために大幅に増加し、パフォーマンスに影響します。



別のオプションは、箱をシミュレートすることです。立方体の平らな表面を取り、その上に木材に似たものを単純に描きます。ボックスをよく見ていないと、違いに気付かないでしょう。



2番目のアプローチを使用します。まず、表面に描画する画像が必要です。このコンテキストでは、この画像をテクスチャと呼びますが、オブジェクトのテクスチャとは反対です-ラフまたはソフトなどです...「木製ボックス」の





テクスチャは 次のとおりです。Filter Forge Texture-Attribution 2.0 Generic（CC BY 2.0）



次に、モデルにテクスチャを重ねる方法を指定する必要があります。各三角形のオーバーレイを指定して、三角形の各頂点に重ねられたテクスチャポイントを示します：







問題なく、テクスチャを変形したり、テクスチャの一部のみを使用したり、各頂点のテクスチャ座標を変更したりできることに注意してください。



このオーバーレイを設定するには、このテクスチャのポイントを定義する座標系を使用します。これらの座標を呼び出す$$$u$ そして $$v、混同しないように$v$$$$x$$$y、通常はキャンバス上のピクセルです。また、それを発表します$y$$$$u$ そして $$vは範囲内の実数値です$v$$$[ 0 、1 ]の画素におけるテクスチャ画像の解像度に依存しています。これはいくつかの理由で非常に便利です。たとえば、使用可能なRAMの量に応じて、モデル自体を変更せずに低解像度または高解像度のテクスチャを使用できます。テクスチャマッピングの基本的な考え方は簡単です。座標を計算します$[0, 1]$



$$（ U 、 V ）三角形の各画素対応のためのテクセル（すなわち、TEX-温度のELテクスチャのement）とその色画素を塗りつぶします。セットセット$（u、v）$$$テクスチャサイズ（ U 、 v ）$（u、v）$$$（w 、h ）はテクセルに重ねられます$(w, h)$$$$(u (w-1), v (h-1))$ 。



しかし、座標しかありません $$$u$ そして $$v三角形の3つの頂点の場合、それらは各ピクセルに必要です... はい、線形補間。属性の割り当てを使用して値を補間します$v$$$$u$ そして $$v三角形のエッジに沿って$v$$$（ U 、 v ）各ピクセル。テクスチャから取得した適切な色でピクセルを塗りつぶし（おそらく照明の効果で）、......通常の結果を取得します。ボックスは非常によく見えますが、斜めのボードを見ると、それらが少し変形していることが明らかになります。間違いは何ですか？私たちは再び間違った仮定に閉じ込められています。私たちは信じています$（u、v）$















$$$u$ そして $$v画面に沿って直線的に変化します。明らかに、そうではありません。黒と白の縦縞が交互に描かれた非常に長い廊下の壁を見てください。壁が取り除かれると、ますます微妙な縞が見えるはずです。ただし、座標が$v$$$uは線形に変化します$u$$$x ′の場合、これは当てはまりません。この状況は、「バッファリングの深さ」の章で出会った状況と非常に似ており、解も非常に似ています。$x'$







$$$u$ そして $$vは画面座標が非線形であり、$v$$$$u \over z$ そして $$vzは線形です（注：この証明は証明と非常に似ています$v \over z$$$1z：と仮定する${1 \over z}$$$uは3D空間で線形に変化し、置き換えます$u$$$$X$ そして $$画面スペースでの表現の Y。）。すでに値を補間しているので$Y$$$1各ピクセルに対してz、次に補間する$1 \over z$$$$u \over z$ そして $$$v \over z$ 取得する $$$u$ そして $$$v$ ：

$$

$$u = { {u \over z} \over {1 \over z}}$$

$$

$$v = { {v \over z} \over {1 \over z}}$$

同時に、期待される結果が得られます。







ソースコードと作業デモ>>