🧑🏾 👨🏼‍🚀 🍡 単純な座標系ではなく、黄金の座標系 ☘️ 👨‍❤️‍👨 🔬

ペンローズのモザイクの1つでは、角度が異なる2つの菱形のみが使用されます。これらの要素から、任意のサイズの非周期的なモザイクを構築できます。それを表示するために、座標を分析的に提供しようとしました。

一方の菱形の角度の分布は、1：4、36°：144°、他の2：3、72°：108°です。菱形の角度は、1回転の10分の1の倍数、36°です。

通常の十角形の角の座標を定義します。

学位	cos	罪
0	1	0
36	0.809017	0.587785
72	0,309017	0.951056

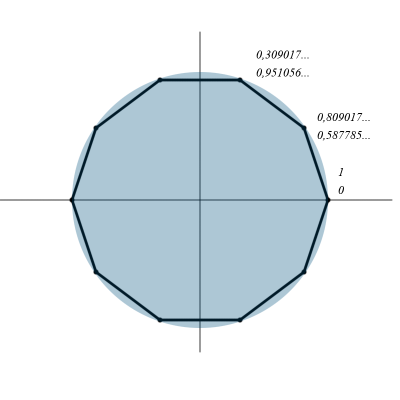
残りは対称的で、符号のみが変わります。

角度36°と72°の余弦が0.5異なることがすぐにわかります。これは非常に重要な事実です！

座標の絶対値は、横座標と縦座標の両方で正確に3つの部分です。 3つすべては、整数係数を持つ2つの係数として表すことができます。

横座標の場合、これは簡単です。値の中にはゼロがあり、これはゼロ係数で表されます。縦座標の中で、3番目の単位は他の2つに比例しません。しかし、座標の差は0.5なので、この差は係数の1つになり、2番目の係数はより小さな値になります。値1は2の係数で取得されます。

* 36°	x		y
	C _xa = 0.5	C _xb = 0.309017	C _ya = 0.951056	C _xb = 0.587785
0	2	0	0	0
1	1	1	0	1
2	0	1	1	0
3	0	-1	1	0
4	-1	-1	0	1
5	-2	0	0	0
6	-1	-1	0	-1
7	0	-1	-1	0
8	0	1	-1	0
9	1	1	0	-1

そして、それは整数座標系があることを意味します。

\ {x_1、x_2、y_1、y_2 \} =（C_ {xa} x_1 + C_ {xb} x_2、C_ {ya} y_1 + C_ {yb} y_2）

$\ {x_1、x_2、y_1、y_2 \} =（C_ {xa} x_1 + C_ {xb} x_2、C_ {ya} y_1 + C_ {yb} y_2）$

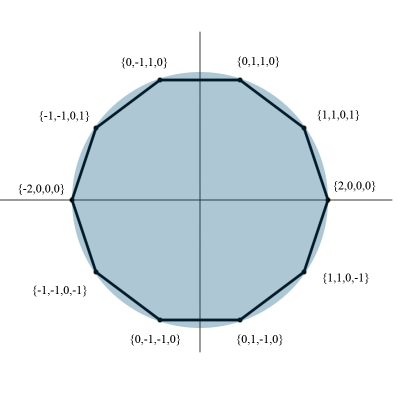
係数は同じ係数でペアごとに異なります。これは黄金比の比率です。

C_{x b} = v a r p h i C_{x a}

$C_ {xb} = \ varphi C_ {xa}$

C_{y b} = v a r p h i C_{y a}

$C_ {yb} = \ varphi C_ {ya}$

v a r p h i = f r a c s q r t 5 - 1 2

$\ varphi = \ frac {\ sqrt {5}-1} {2}$

係数の正確な表現を導き出すことができます。

C_{x a} = f r a c 12

$C_ {xa} = \ frac {1} {2}$

C_{x b} = f r a c v a r p h i 2

$C_ {xb} = \ frac {\ varphi} {2}$

C_{y a} = f r a c s q r t 3 + v a r p h i 2

$C_ {ya} = \ frac {\ sqrt {3 + \ varphi}} {2}$

C_{y b} = f r a c s q r t 2 - v a r p h i 2

$C_ {yb} = \ frac {\ sqrt {2-\ varphi}} {2}$

次は、ゴールデンセクションの魔法です。

v a r p h i^{2} = 1 - v a r p h i

$\\\ varphi ^ 2 = 1- \ varphi$

（ a + b v a r p h i ） c d o t v a r p h i = a c d o t v a r p h i + b （ 1 - v a r p h i ） = b + （ a - b ） v a r p h i

$\\（a + b \ varphi）\ cdot \ varphi = a \ cdot \ varphi + b（1- \ varphi）= b +（a-b）\ varphi$

（ a + b v a r p h i ） / v a r p h i = （ b + a ） + a v a r p h i

$\\（a + b \ varphi）/ \ varphi =（b + a）+ a \ varphi$

（ 3 + v a r p h i ） （ 2 - v a r p h i ） = 6 + 2 v a r p h i - 3 v a r p h i - v a r p h i^{2} = 6 - v a r p h i - （ 1 - v a r p h i ） = 5

$\\（3+ \ varphi）（2- \ varphi）= 6 + 2 \ varphi-3 \ varphi- \ varphi ^ {2} = 6- \ varphi-（1- \ varphi）= 5$

したがって、多くのパターン：

自明：

C_{x a} c d o t C_{x a} = C_{x a} / 2

$C_ {xa} \ cdot C_ {xa} = C_ {xa} / 2$

C_{x a} c d o t C_{x b} = C_{x b} / 2

$C_ {xa} \ cdot C_ {xb} = C_ {xb} / 2$

C_{x a} c d o t C_{y a} = C_{y a} / 2

$C_ {xa} \ cdot C_ {ya} = C_ {ya} / 2$

C_{x a} c d o t C_{y b} = C_{y b} / 2

$C_ {xa} \ cdot C_ {yb} = C_ {yb} / 2$

係数の比率が等しいため：

C_{x b} c d o t C_{y a} = v a r p h i c d o t C_{x a} c d o t C_{y a} = v a r p h i c d o t C_{y a} / 2 = C_{y b} / 2

$C_ {xb} \ cdot C_ {ya} = \ varphi \ cdot C_ {xa} \ cdot C_ {ya} = \ varphi \ cdot C_ {ya} / 2 = C_ {yb} / 2$

C_{x b} c d o t C_{y b} = v a r p h i c d o t C_{x a} c d o t v a r p h i c d o t C_{y a} = （ 1 - v a r p h i ） c d o t C_{y a} / 2 = （ C_{y a} - C_{y b} ） / 2

$C_ {xb} \ cdot C_ {yb} = \ varphi \ cdot C_ {xa} \ cdot \ varphi \ cdot C_ {ya} =（1-\ varphi）\ cdot C_ {ya} / 2 =（C_ {ya }-C_ {yb}）/ 2$

係数の二乗：

C_{x b} c d o t C_{x b} = （ 1 - v a r p h i ） / 4 = （ C_{x a} - C_{x b} ） / 2

$C_ {xb} \ cdot C_ {xb} =（1-\ varphi）/ 4 =（C_ {xa}-C_ {xb}）/ 2$

C_{y a} c d o t C_{y a} = （ 3 + v a r p h i ） / 4 = （ 3 C_{x a} + C_{x b} ） / 2

$C_ {ya} \ cdot C_ {ya} =（3 + \ varphi）/ 4 =（3 C_ {xa} + C_ {xb}）/ 2$

C_{y b} c d o t C_{y b} = （ 2 - v a r p h i ） / 4 = （ 2 C_{x a} - C_{x b} ） / 2

$C_ {yb} \ cdot C_ {yb} =（2-\ varphi）/ 4 =（2 C_ {xa}-C_ {xb}）/ 2$

アートワーク：

C_{y a} c d o t C_{y b} = s q r t （ 3 + v a r p h i ） （ 2 - v a r p h i ） / 4 = s q r t 5 / 4 = （ 1 + 2 v a r p h i ） / 4 = （ C_{x a} + 2 C_{x b} ） / 2

$C_ {ya} \ cdot C_ {yb} = \ sqrt {（3 + \ varphi）（2-\ varphi）} / 4 = \ sqrt {5} / 4 =（1 + 2 \ varphi）/ 4 =（ C_ {xa} + 2 C_ {xb}）/ 2$

これらのプロパティに基づいて、ベクトルの整数乗算の行列を作成できます。

const crd vmul[16] = { { 1, 0, 0, 0}, { 0, 1, 0, 0}, { 0, 0, 1, 0}, { 0, 0, 0, 1}, { 0, 1, 0, 0}, { 1,-1, 0, 0}, { 0, 0, 0, 1}, { 0, 0, 1,-1}, { 0, 0, 1, 0}, { 0, 0, 0, 1}, {-3,-1, 0, 0}, {-1,-2, 0, 0}, { 0, 0, 0, 1}, { 0, 0, 1,-1}, {-1,-2, 0, 0}, {-2, 1, 0, 0} };

そして、すべての乗算は

 int* vm = (int*)vmul; for(int i = 0; i < 4; i++) for(int j = 0; j < 4; j++) for(int k = 0; k < 4; k++) v3[k] += v1[i] * v2[j] * vm[(i * 4 + j) * 4 + k];

このシステムのベクトル単位は{2,0,0,0}として表されます。そのようなユニットの単純な転置の後、{4,0,0,0}を取得します。したがって、係数の各式にあった2つへの分割は、正規化として個別に行われます。

 for(int i = 0; i < 4; i++) v3[i] /= 2;

この座標系の特徴は、与えられた精度で平面全体をカバーすることです。任意の数のステップを繰り返して、10方向のいずれかを選択し、整数座標のままにすることができます。

しかし、座標のすべての組み合わせが開始位置から到達可能な場所を決定するわけではありません。

座標の展開の1ステップについては、次のとおりです：{2,0,0,0}、{1,1,0,1}、{0,1,1,0}、{0、-1,1,0}、{ -1、-1,0,1}、{-2,0,0,0}、{-1、-1,0、-1}、{0、-1、-1,0}、{0、 1、-1.0}、{1,1.0、-1}。これらの手順の任意の組み合わせが有効です。

単一のステップ{2,0,0,0}の組み合わせとともに

{0,1,1,0}-{0,1、-1,0} = {0,0,2,0}、

{1,1,0,1}-{1,1,0、-1} = {0,0,0,2}、

{1,1,0,1} + {1,1,0、-1}-{2,0,0,0} = {0,2,0,0}

つまり、任意の単一の座標を2ずらすことができるため、到達可能性は座標のグループパリティによってのみ影響を受けます。達成可能な組み合わせは4つあります：ゼロ：{0,0,0,0}、単一ステップから：{1,1,0,1}、{0,1,1,0}、およびそれらの組み合わせ：{1,0、 1,1}。

ご覧のように、横座標のグループパリティは、縦座標のグループパリティと一意に相互接続されています。これは、垂直座標が4つのタイプに分割され、水平座標も4つのタイプに分割され、ポイントが正しく結合された場合にのみ座標系に属することを意味します。

任意の点に近づくには、グループパリティを考慮して、各座標を適切な整数因子に分解する必要があります。

一般に、整数の座標値と36度の回転を組み合わせた座標系があります。彼女を連れ出したとき、私は彼女のことを前に知らなかったことに驚きました。しかし今、彼女に関する記事がHabréにあります。

\ frac {{\ displaystyle \ frac {5- \ sqrt5} {5+ \ sqrt5}}-\ sqrt {\ displaystyle \ frac {5+ \ sqrt5} {5- \ sqrt5}} {\ displaystyle \ frac { 5+ \ sqrt5} {5- \ sqrt5} + \ sqrt {\ frac {5- \ sqrt5} {5+ \ sqrt5}} + \ frac {5- \ sqrt5} {5+ \ sqrt5} = 0

$\ frac {{\ displaystyle \ frac {5- \ sqrt5} {5+ \ sqrt5}}-\ sqrt {\ displaystyle \ frac {5+ \ sqrt5} {5- \ sqrt5}} {\ displaystyle \ frac { 5+ \ sqrt5} {5- \ sqrt5} + \ sqrt {\ frac {5- \ sqrt5} {5+ \ sqrt5}} + \ frac {5- \ sqrt5} {5+ \ sqrt5} = 0$

f r a c 5 - s q r t 5 5 + s q r t 5 + s q r t f r a c 5 - s q r t 5 5 + s q r t 5 o v e r s e t 1 = f r a c 5 + s q r t 5 5 - s q r t 5 - s q r t f r a c 5 + s q r t 5 5 - s q r t 5

$\ frac {5- \ sqrt5} {5+ \ sqrt5} + \ sqrt {\ frac {5- \ sqrt5} {5+ \ sqrt5}} overset1 = \ frac {5+ \ sqrt5} {5- \ sqrt5 }-\ sqrt {\ frac {5+ \ sqrt5} {5- \ sqrt5}}$

単純な座標系ではなく、黄金の座標系

More articles: