🔁 👌🏾 🚌 計画および制約プログラミングタスク 🙌 🚀 ➗

JAVA、Python、Ruby、PHP、C＃、C ++などのような人気のあるツールがたくさんある場合、ほとんど全能だと感じます。タクシーの開発への標準的なアプローチ。ただし、特定の種類のタスクに出会うまでです。

最適なプログラムの書き方を考えてください...

•数独タイプのパズルまたは8人の女王の課題を解決します。

•特定のリソースセット間でタスクを分散します。

•クラスのスケジュールを計算します。

•トラフィックの効果的なルートを決定します。

•勤務スケジュールなどを作成します。

制約のプログラミングと複雑な組み合わせ計画問題の解決があなたの最強の側面ではない場合、この記事はあなたのためだけのものです。

例として、スケジューリングのタスクの1つである、デューティスケジュールの計算を考えてみましょう。チャート計算アルゴリズムを選択する際にプログラマが抱える問題は何ですか？一見、すべてが非常に簡単です。簡単なアルゴリズムを使用できます。従業員間で職務をランダムにまたはより適切に順番に均等に配分します。

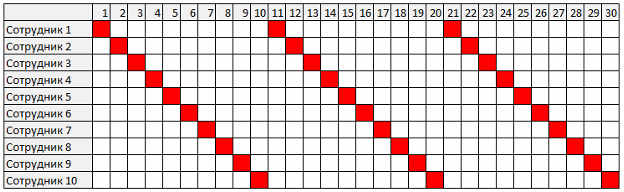
これは理想的なオプションです。ただし、実際には、すべてがはるかに複雑です。通常、考慮しなければならない多くの追加条件があります。従業員は休暇に出たり、日程を変更したりします。その結果、シフトが現れます。従業員の希望を考慮したい場合、職務が複数のシフトに分割されている場合、または人の選択は資格のレベルなどに応じてさらに難しくなります。ある時点で、単純なアルゴリズムが機能しなくなります。他の方法を試すこともできます-多くの可能な組み合わせの中から最適なソリューションを探します。ただし、ここで別の問題が発生します。

すべての制限に準拠したアテンダントの最適な配布という問題自体は新しいものではありません。それは40年以上前から存在し、ナーススケジューリング問題（NSP）として知られています。

難しさは何ですか？計画タスクは、数学の組み合わせのセクションに関連しています。通常、この種のタスクには1つではなく、多くのソリューションがあり、時には非常に大きなソリューションもあります。簡単な例。毎日10人の従業員のうち1人が勤務している30日間の勤務スケジュールをいくつ作成できますか？ 10〜30度（数億）の方法であることがわかります。条件が似ているが、その日が3つのシフト（シフトごとに1人の従業員）に分割されている場合、

A_{10}^{3} = 8 * 9 * 10 = 720

$A ^ {3} _ {10} = 8 * 9 * 10 = 720$ 30度のオプション。徹底的な検索の方法によって、このような多数の組み合わせの中から最適なオプションを見つけることは、最も強力なコンピューターを超えています。

別の難しさ：ほとんどの計画タスクは、 NP困難クラスの複雑な組み合わせ問題の一部です。悪いニュースは、NP困難な問題には、妥当な時間内に証明可能な最適な解を見つけることができる効果的な普遍的なアルゴリズム（多項式）がないことです。

理論的にはこのようなアルゴリズムが存在する可能性がありますが、問題は未解決のままです（クラスPおよびNPの等価性を参照）。発行価格は1,000,000ドルです（ Millennium Tasksを参照）。

幸いなことに、魔法の薬や特効薬はありませんが、まだ道はあります。許容できる時間内にこのタイプの問題に最適なソリューションを見つけるためのさまざまなアプローチがあります。

制約を満たす問題としての組み合わせ問題

組み合わせ問題を解決するために、制約充足問題（CSP）として表すことができます。 CSPは、単純な記述スキームで構成されます。変数（変数）のリストには、それぞれに可能な値（ドメイン）のセットが与えられ、変数が満たす必要のある制約（制約）のリストがあります。 CSPの解決策は、指定された制約の条件に従って変数が取ることができるすべての可能な値を見つけることです。

単純なCSPの例

変数：

$X \ in \左\ {1,2,3 \右\}$

$Y \ in \左\ {1,2 \右\}$

$Z \ in \左\ {1,2,3 \右\}$
制限事項：

$X \ neq Y$

$X = Z$

$Y <Z$
解決策：

$X = 2、Y = 1、Z = 2$

$X = 3、Y = 1、Z = 3$

$X = 3、Y = 2、Z = 3$

CSPは特定の決定アルゴリズムを定義しません。多くの異なるアプローチがあります。それらのいくつかは次のように表すことができます...

整数計画法：
- Gomoriアルゴリズム（切断面法）;
- 分岐限定メソッド。
ローカル検索アルゴリズム（ローカル検索）：
- アニーリングをシミュレートするためのアルゴリズム（シミュレーテッドアニーリング）;
- しきい値受け入れアルゴリズム。
- 禁止付き検索（タブー検索）;
- 遺伝的アルゴリズム ;
- 最小競合アルゴリズム。
ニューラルネットワーク

たとえば、検索ツリーとリターン検索アルゴリズムを組み合わせた特殊なCSPメソッドがよく使用されます。

CSPおよび制約プログラミング

計画とスケジューリングでは、制約プログラミング（CP）テクノロジーが適切であり、よく使用されます。大規模な組み合わせ問題の効果的な解決のためのアルゴリズムのコンピューター実装。通常の形式の命令型プログラミングとは異なり、CPは宣言型を使用します。これにより作業が簡素化されます。問題を記述するだけで、すべての計算と値の検索は、効果的な計算アルゴリズムを含むソルバーによって実行されます。

制約でのプログラミングは、制約を満たすタスクと密接に関連しています。したがって、例として前述したCSPは、プログラムとして非常に簡単に表示できます。

たとえば、MiniZincでは、次のようになります。

% VARIABLES var {1,2,3}: X; var {1,2}: Y; var {1,2,3}: Z;  % CONSTRAINTS constraint X != Y; constraint X = Z; constraint Y < Z;  % SOLVER solve satisfy;  % OUTPUT output ["X=", show(X), " Y=", show(Y), " Z=", show(Z)];

作業が完了すると、プログラムは指定された制限に従って変数のすべての有効な値を表示します。


      

        
        
        
      

     X=2 Y=1 Z=2 
      

        
        
        
      

     ---------- 
      

        
        
        
      

     X=3 Y=1 Z=3 
      

        
        
        
      

     ---------- 
      

        
        
        
      

     X=3 Y=2 Z=3 
      

        
        
        
      

     ----------

制約のあるプログラミングでは、CPサポートを備えた個別のプログラミング環境と、通常のプログラミング言語のプラグインライブラリの両方が使用されます。

接続されたライブラリ：

Google最適化ツール（ORツール）（C ++、Python、.Net、Java）
Gecode （C ++、 Gecode_Interfaces ）
チャフ（C ++）
コインOR CBC （C ++）
OptaPlanner （Java）
JaCoP （Java）
チョコ（Java）
CHIP V5 （C ++）
Microsoft Solver Foundation （.Net）

個別のプログラミング環境：

CSP形式の勤務時間

たとえば、勤務スケジュールの計算の問題を考えてみましょう。 CSPモデルとして想像してください。タスクの条件は意図的に簡素化され、もっぱら探索的な性格を持ちます。

凡例

30日間、10人の勤務スケジュールを計算する必要があります。
毎日、2人の従業員が職務に参加し、1人がメインの職務を引き継ぎ、もう1人が予備役を務めます。
期間全体の各従業員は、主任務の総数を3人以上にする必要があります。
メインの勤務の翌日、従業員はスタンバイ勤務に入り、その後1日以上休みます。

1.ソースデータ

n-請求期間の日数（n = 30）
m-勤務中の人数（m = 10）
dはその日のインデックスです（d = 1、...、n）
e-従業員インデックス（e = 1、...、m）

2.変数（変数）

一連の変数Xを2次元行列の形式で定義します。各行の変数の順序は、特定の従業員の勤務日数に対応しています。

u n d e r s e t （ m t i m e s n ） X = b e g i n b m a t r i x x_{1, 1} x_{1, 2} . . . x_{1 、 n} x_{2 、 1} x_{2, 2} . . . x_{2 、 n} . . . x_{m 、 1} x_{m 、 2} . . . x_{m 、 n} e n d b m a t r i x

$\ underset {（m \ times n）} X = \ begin {bmatrix} x_ {1,1} \ \ x_ {1,2} \ \ ... \ \ x_ {1、n} \\ x_ {2 、1} \ \ x_ {2,2} \ \ ... \\ x_ {2、n} \\ ... \\ x_ {m、1} \ \ x_ {m、2} \ \ ... \ \ x_ {m、n} \ end {bmatrix}$

変数の有効なドメイン：

x_{e 、 d} b e g i n c a s e s 1 、 ＆ i f e m p l o y e e e m a i n d u t y o n d a y d 2 、 ＆ i f e m p l o y e e e r e s e r v e o n d a y d 3 、 ＆ \従 業 員 e e n d c a s e s $ か ら \義 務 \日 d \を 無 料

$x_ {e、d} \ begin {cases} 1、＆if \ employee \ e \ main \ duty \ on \ day \ d \\ 2、＆if \ employee \ e \ reserve \ on \ day \ d \\ 3、＆\従業員\ e \ end {cases} $から\義務\日\ d \を無料$

3.制限（制約）

毎日、1人の従業員のみが主任役員になることができます。

s u m_{e = 1}^{m} [x_{e 、 d} = 1] = 1 \（ d = 1 、 2 、 . . . 、 n ）

$\ sum_ {e = 1} ^ m [x_ {e、d} = 1] \ = 1 \ \ \ \ \（d = 1、2、...、n）$

角括弧- アイバーソン表記法での指定

$[P] = b e g i n c a s e s 1 、＆ i f P t r u e 0 、＆ i f P f a l s e e n d c a s e s$
$[P] = \ begin {cases} 1、＆if \ P \ true \\ 0、＆if \ P \ false \ end {cases}$

毎日、1人の従業員のみが待機役員になることができます。

s u m_{e = 1}^{m} [x_{e 、 d} = 2] = 1 \（ d = 1 、 2 、 . . . 、 n ）

$\ sum_ {e = 1} ^ m [x_ {e、d} = 2] \ = 1 \ \ \ \ \（d = 1、2、...、n）$

期間全体の各従業員の主な勤務時間数は3以上でなければなりません。

s u m_{d = 1}^{n} [x_{e 、 d} = 1] g e q 3 \（ e = 1 、 2 、 . . . 、 m ）

$\ sum_ {d = 1} ^ n [x_ {e、d} = 1] \ \ geq 3 \ \ \ \ \（e = 1、2、...、m）$

決定論的な有限状態マシンを定義します。職務の分配の順序を説明しましょう。主要な任務の後、従業員は待機職役員となり、1日以上の休憩が続きます。状態間の遷移が示されます：メイン= 1-メインデューティ、リザーブ= 2-スタンバイデューティ、オフ= 3-休息日。

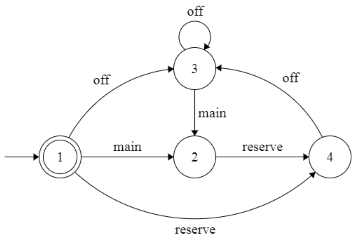
遷移表の形式でのマシンの状態の説明：

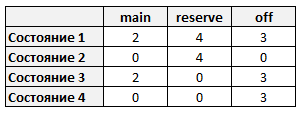
問題はさまざまな方法で定式化できます。たとえば、1と0の値ドメイン（3種類のシフトの3番目の次元）を持つ3次元マトリックスの形式のX値のセットを想像してください。または、職務の種類ごとに、個別の変数を定義します。

MiniZincでの勤務スケジュールの実用的な実装

そして今、おそらく最も興味深い。特定のCSP条件に従って勤務スケジュールを計算する実際のプログラムを作成します。制限のあるプログラミング環境として、MiniZincを使用します。

MiniZincは、高レベルのオープンソース制約モデリング言語です。他のCPプログラミング環境とは異なり、完全にソルバーに依存しません。 MiniZincを使用すると、さまざまな複雑さのモデルを簡単に作成し、サードパーティのソルバーで実験することができます。言語兵器には、多数のグローバル制約（グローバル制約MiniZinc ）を備えたライブラリが含まれており、カスタム制約（述語）を作成することもできます。これにより、適用された問題のモデリングが大幅に簡素化されます。

ソルバーの独立性は、MiniZincプログラムを下位レベルのFlatZincコードに変換することにより実現されます。インターフェイスを介したFlatZincは、多数のソルバーによってサポートされています。

MiniZincは、ほとんどのプラットフォーム（Windows、Mac OS、Linux）で使用でき、独立したIDEも備えています。

MiniZinc言語のより詳細な紹介については、 MiniZincチュートリアルを読むことを強くお勧めします。このチュートリアルでは、言語のすべての機能を非常に理解しやすい形式で説明し、多くの例があります。

CSP勤務スケジュールモデルをMiniZincプログラムコードに書き換え、プログラムを実行し、問題を解決します。

 include "regular.mzn"; %-------------------------------------------------- % 1. INITIAL DATA.   %-------------------------------------------------- int: n = 30; int: m = 10; set of int: D = 1..n; set of int: E = 1..m; %     array[1..4, 1..3] of int: dfa_states = [|2, 4, 3 |0, 4, 0 |2, 0, 3 |0, 0, 3 |]; %------------------------------------------------- % 2. VARIABLES.  %------------------------------------------------- array[E, D] of var 1..3: X; %------------------------------------------------- % 3. CONSTRAINTS.  %------------------------------------------------- % 3.1            % 3.2            %        /\ constraint forall(d in D)( sum(e in E)( bool2int( X[e, d] = 1 )) = 1 /\ sum(e in E)( bool2int( X[e, d] = 2 )) = 1 ); % 3.3       ,           constraint forall(e in E)( sum(d in D)( bool2int( X[e, d] = 1 )) >= 3 /\ regular( [X[e, d] | d in D], 4, 3, dfa_states, 1, 1..4 ) % regular -  ,          (dfa_states) ); %------------------------------------------------- % SOLVE %------------------------------------------------- solve satisfy; %------------------------------------------------- % OUTPUT %------------------------------------------------- array[1..3] of string: rest_view = ["M", "R", "-"]; output [ rest_view[fix(X[e, d])] ++ " " ++ if d = n then "\n" else "" endif | e in E, d in D ];

プログラムを完了すると、勤務スケジュールの可能なオプションの1つが得られます。各従業員の職務配分の順序（水平線）。ここで、M（メイン）-メインの職務、R（リザーブ）-スタンバイの職務、「-」-従業員は勤務していない

MR - - - - - - MR - - - - MR - - - - - - - - - - - - - - 
      

        
        
        
      

     R - - - - MR - - - MR - - - - - - - - - MR - - - - - - - 
      

        
        
        
      

     - - - - - - - MR - - - - - - MR - - - - - - - MR - - - - 
      

        
        
        
      

     - - - - - - MR - - - - - - - - MR - - - - - - - - MR - - 
      

        
        
        
      

     - MR - - - - - - - - - - - - - - - - - MR - MR - - - - - 
      

        
        
        
      

     - - MR - - - - - MR - - - - - - - - - - - MR - - - - - - 
      

        
        
        
      

     - - - - - - - - - - - - MR - - - - - MR - - - - - - MR - 
      

        
        
        
      

     - - - - MR - - - - - MR - - - - - - - - - - - - - - - MR 
      

        
        
        
      

     - - - - - - - - - - - - - MR - - - MR - - - - - - - - - M 
      

        
        
        
      

     - - - MR - - - - - - - - - - - - MR - - - - - - MR - - -

または、より理解しやすい方法で表示される場合、次のようになります。

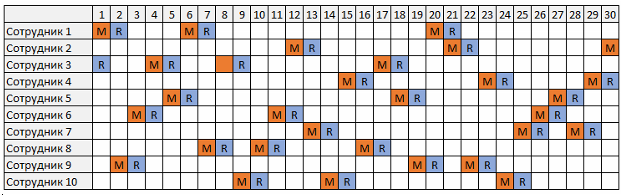
従業員が勤務しないはずの休暇日が事前にわかっている場合、または特定の日付に特定の従業員の勤務を修正する必要がある場合は、追加の制限を通じてこれを行うことができます。たとえば、5番目の従業員が1日目に主任役員であり、2番目の従業員が6日目に勤務していないように、制限を設定します。

制約X [5.1] = 1 / \ X [2.6] = 3;

プログラムのもう少し複雑なバージョン（Hakan Kjellerstrand）がここにあります。

おわりに

ハンマーの幸せな所有者は、ツールが問題を解決するのに適しているという幻想を抱くかもしれません。しかし、ハンマーは普遍的ではなく、場合によってはその利点が完全に明白ではありません。そして、そのようなケースはたくさんあります。そのため、プログラミングでは、特殊なアプローチを使用しないと、一部のタスクが誤って解決されるか、最適に解決されません。制約条件でのプログラミングは強力なツールであり、多数の実用的な組み合わせの問題を効果的に解決するのに役立つ別のパラダイムです。

Hakan Kjellerstrandブログで制約プログラミングに関する多くの有用な情報を見つけることができ、多くのMiniZincサンプルタスクがここまたはここで見つかります。

関連リンク：

ナーススケジューリングの問題

制限の満足

制限されたプログラミング

MiniZincホームページ

Minizincチュートリアル

MiniZincチャレンジ

計画および制約プログラミングタスク

制約を満たす問題としての組み合わせ問題

CSPおよび制約プログラミング

CSP形式の勤務時間

MiniZincでの勤務スケジュールの実用的な実装

おわりに

More articles: