この記事は、 レイトレーシングとラスター化の2つの主要部分に分かれており、データから美しい画像を取得する2つの主要な方法について説明しています。 「 一般概念」の章では、これら2つの部分を理解するために必要ないくつかの基本概念を紹介します。



この作業では、速度ではなく、概念の明確な説明に焦点を当てます。 サンプルコードは最も理解しやすい方法で記述されていますが、アルゴリズムを実装するのに必ずしも最も効率的ではありません。 それを実装する多くの方法があります;私は理解するのが最も簡単なものを選びました。



この作業の「最終結果」は、レイトレーサーとラスタライザーの2つの完全に機能する完全なレンダラーになります。 これらは非常に異なるアプローチを使用しますが、単純なシーンをレンダリングする場合、同様の結果が得られます。







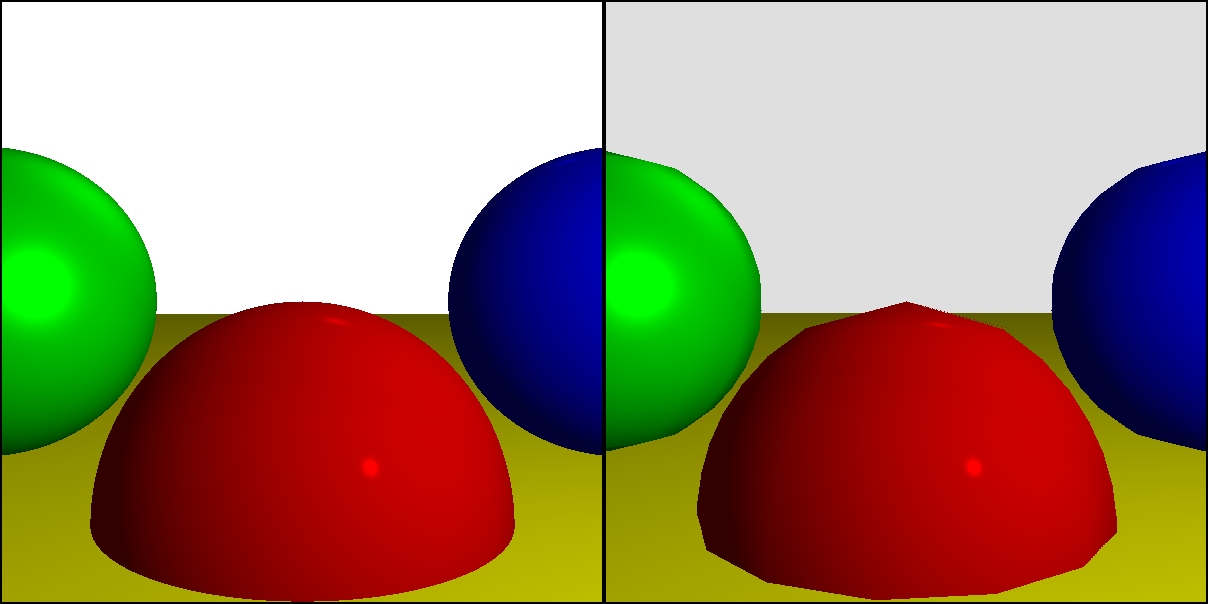
それらの機能は多くの点で重複していますが、類似しているわけではないため、この記事ではその長所について説明します。







この記事では、非公式の擬似コードの形式でサンプルコードを提供します。また、 canvas



要素でレンダリングされ、ブラウザーで実行できる完全に機能するJavaScript実装も含まれています。

この記事を読む理由

この作業により、ソフトウェアレンダラーを作成するために必要なすべての情報が得られます。 ビデオプロセッサのこの時代では、純粋なソフトウェアレンダラーを作成する説得力のある理由を見つけることはほとんどありませんが、それを作成した経験は次の理由から価値があります。

1. シェーダー 。 最初のビデオプロセッサでは、アルゴリズムはハードウェアにハードコーディングされていましたが、現代のビデオプログラマーは独自のシェーダーを作成する必要があります。 言い換えれば、ビデオプロセッサで実行されるようになってからでも、レンダリングソフトウェアの大部分を実装する必要があります。
2. 理解します。 既製のパイプラインを使用するか、独自のシェーダーを作成するかに関係なく、舞台裏で何が行われているのかを理解することで、既製のパイプラインをより有効に使用し、シェーダーをより適切に作成できます。
3. 興味深い 。 コンピュータサイエンスの分野では、コンピュータグラフィックスが提供する目に見える結果を即座に得ることができる分野はほとんどありません。 最初のSQLクエリの実行を開始した後の誇りは、最初に反映を正しく反映できると感じる方法とは比べ物になりません。 大学でコンピューターグラフィックスを5年間教えました。 私は学期ごとに学期ごとに楽しんでいることにしばしば驚かされました：最後に、私の努力は、最初のレンダリングをデスクトップの壁紙として使用できる学生の喜びによって正当化されました。

一般的な概念

キャンバス

このプロセスでは、 キャンバスにオブジェクトを描画します 。 キャンバスは、個別に色付けできるピクセルの長方形の配列です。 画面に表示したり、紙に印刷したり、その後のレンダリングのテクスチャとして使用したりしますか？ これは私たちの作業にとって重要ではありません。この抽象的な長方形のピクセル配列で画像をレンダリングすることに焦点を合わせます。



この記事のすべては、単純なプリミティブから作成します。キャンバス上にピクセルを指定の色で描画します。

  canvas.PutPixel（x、y、色） 

次に、このメソッドのパラメーターである座標と色を調べます。

座標系

キャンバスにはピクセル単位で特定の幅と高さがあり、これを呼び出します $$$C_w$ そして $$$C_h$ 。 そのピクセルを操作するには、任意の座標系を使用できます。 ほとんどのコンピューター画面では、原点は左上隅にあります $$$x$ 右に増加し、 $$$y$ -ダウン：







これは、ビデオメモリの構成を考慮した非常に自然な座標系ですが、人々にとってはあまり馴染みがありません。 代わりに、通常紙にグラフを描くために使用される座標系を使用します：中心の原点 $$$x$ 右に増加し、 $$$y$ -上：







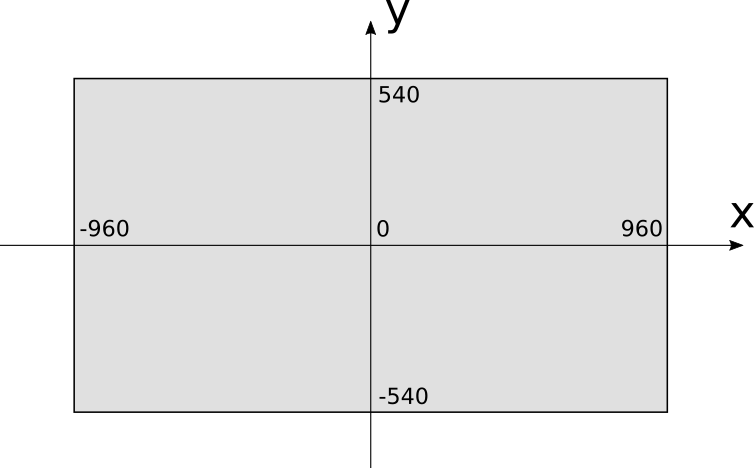
この座標系を使用する場合、座標 $$$x$ 範囲内にある $$$[{-C_w \ over 2}、{C_w \ over 2}]$ 、および座標 $$$y$ -範囲内 $$$[{-C_h \ over 2}、{C_h \ over 2}]$ （注：厳密に言えば、または $$${-C_h \ over 2}$ 、または $$${C_h \ over 2}$ 範囲外ですが、無視します。）。 簡単にするために、可能な間隔外のピクセルで作業しようとすると、何も起こりません。



例では、キャンバスが画面に描画されるため、ある座標系から別の座標系への変換を実行する必要があります。 画面がキャンバスと同じサイズであると仮定すると、変換式は単純になります。

$$

$$S_x = {C_w \ over 2} + C_x$$

$$

$$S_y = {C_h \ over 2}-C_y$$

カラーモデル

カラーワークの理論は素晴らしいですが、残念ながら、私たちの記事の範囲を超えています。 以下は、私たちにとって重要な側面の簡略版です。



色は、脳が目に入る光子をどのように解釈するかを示します。 これらの光子はさまざまな周波数のエネルギーを運び、私たちの目はこれらの周波数を色と関連付けます。 私たちが知覚する最低エネルギーの周波数は約450 THzで、赤と認識します。 スペクトルのもう一方の端には750 THzがあり、これは「紫色」と見なされます。 これらの2つの周波数の間には、連続した色のスペクトルがあります（たとえば、緑-これは約575 THzです）。



通常の状態では、この範囲外の周波数は確認できません。 より高い周波数はより多くのエネルギーを運ぶため、赤外線放射（450 THz未満の周波数）は無害ですが、紫外線（750 THzを超える周波数）は皮膚を火傷させる可能性があります。



任意の色は、これらの色のさまざまな組み合わせとして説明できます（特に、「白」はすべての色の合計であり、「黒」はすべての色の不在です）。 正確な頻度を示すことで色を説明するのは不便です。 幸いなことに、ほとんどすべての色は、「原色」と呼ばれる3色だけの線形結合として作成できます。

減算カラーモデル

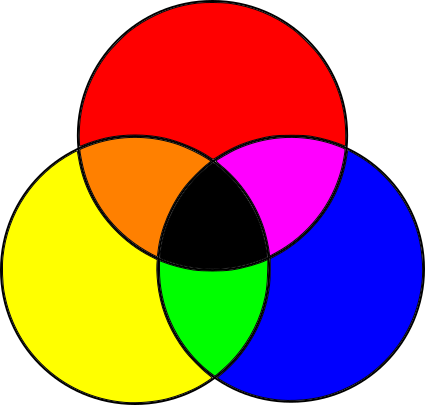
オブジェクトは、さまざまな方法で光を吸収および反射するため、色が異なります。 日光などの白色光から始めましょう（注：日光は真っ白ではありませんが、私たちの目的にとっては十分に近いです）。 白色光には、すべての色の周波数が含まれています。 光がオブジェクトに当たると、オブジェクトの素材に応じて、その表面は周波数の一部を吸収し、他の周波数を反射します。 反射光の一部は目に入り、脳はそれを色に変換します。 何色？ すべての反射周波数の合計（注：熱力学の法則により、残りのエネルギーは失われず、主に熱に変換されます。）



要約すると、すべての周波数で開始し、いくつかの原色を差し引いて別の色を作成します。 周波数を減算するため、このようなモデルは減法混色モデルと呼ばれます。



ただし、このモデルは完全に真実ではありません。 実際、減法混色モデルの原色は、子供や生徒に教えられているように青、赤、黄色ではなく、シアン、マゼンタ、黄色です。 さらに、3つの原色を混合すると、黒に見えないような暗い色が生成されるため、4番目の「原色」として黒が追加されます。 黒は文字Kで示されます。したがって、プリンターに使用されるCMYKカラーモデルを取得します。

加法混色モデル

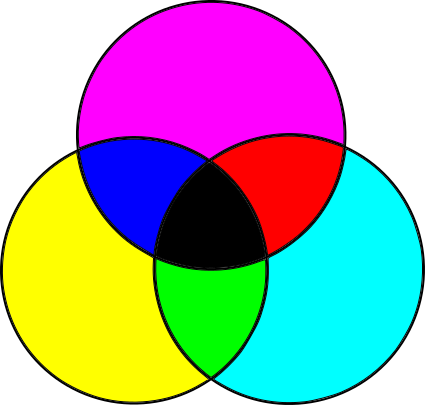
しかし、これは物語の半分にすぎません。 モニター画面は紙の反対です。 紙は光を発しませんが、紙に入射した光の一部を反射するだけです。 一方、画面は黒ですが、画面自体が発光します。 紙の上では、白色光から始めて、不要な周波数を引きました。 画面上で、光の不足から始めて、目的の周波数を追加します。



これには他の原色が必要であることがわかります。 ほとんどの色は、赤、緑、青の異なるサイズを黒の表面に追加することで作成できます。 これは、RGBカラーモデル、 加法カラーモデルです。

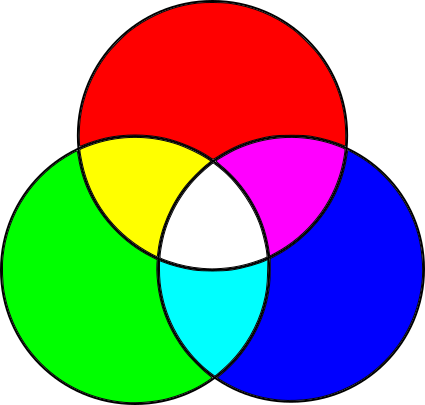
詳細を忘れる

これがすべてわかったので、不要な詳細を選択的に忘れて、仕事に重要なことに集中できます。



ほとんどの色はRGBまたはCMYK（または他の多くのカラーモデル）で表すことができ、ある色空間から別の色空間に変換できます。 私たちの主なタスクは画面上に画像をレンダリングすることなので、RGBカラーモデルを使用します。



前述のように、オブジェクトは入射光の一部を吸収し、残りを反射します。 吸収および反射された周波数は、表面の「色」として認識されます。 この瞬間から、色を単に表面のプロパティとして認識し、吸収された光の周波数を忘れます。

深さと色の表現

前のセクションで説明したように、モニターは赤、緑、青のさまざまな組み合わせから色を作成できます。



明るさはどれくらい違うのでしょうか？ 電圧は連続変数ですが、離散値を使用してコンピューターで色を処理します。 赤、緑、青のさまざまな色合いを設定できるほど、より多くの色を作成できます。



現在最も一般的な形式は、原色ごとに8ビット（ カラーチャネルとも呼ばれます ）を使用しています。 チャネルあたり8ビットは、ピクセルあたり24ビットを提供します。 $$$2 ^ {24}$ さまざまな色（約1670万）。 この形式は888と呼ばれ、作業に使用します。 この形式の色深度は 24ビットであると言えます。



ただし、可能な唯一の形式ではありません。 少し前まで、メモリを節約するために、チャネルごとに5ビットまたは赤に5ビット、緑に6ビット、青に5ビットを割り当てる15ビットと16ビットの形式が一般的でした（この形式は565と呼ばれていました）。 なぜ緑が余分になったのですか？ 私たちの目は赤や青より緑の変化に敏感だからです。



16ビットは私たちに与えます $$$2 ^ {16}$ 花（約65,000）。 これは、24ビットモードの256色ごとに1色を取得することを意味します。 65,000はたくさんありますが、徐々に色が変化する画像では、中間色を表現するのに十分なビットがあるため、1670万色では見えない非常に小さな「ステップ」を見ることができます。 また、1670万色は人間の目で認識できる範囲を超えているため、近い将来、24ビット色を使用し続ける可能性が高くなります。 （注：これは画像表示にのみ適用され、より広い範囲の画像を保存することはまったく異なる問題です。これについては照明の章で説明します。）



色を表すために、3バイトを使用します。各バイトには、8ビットカラーチャネルの値が含まれます。 テキストでは、色を次のように指定します $$$（R、G、B）$ -例えば $$$（255、0、0）$ -それは純粋な赤い色です。 $$$（255、255、255）$ -白、そして $$$（255、0、128）$ -赤紫色。

カラーマネジメント

いくつかの操作を使用して色を制御します（注：線形代数を知っている場合は、色を3次元色空間のベクトルとして認識します。この記事では、線形代数に不慣れな読者に使用する操作を紹介します）。



各色チャンネルを定数で増やすことで、色の明るさを増やすことができます。

$$

$$k（R、G、B）=（kR、kG、kB）$$

カラーチャネルを個別に追加することで、2つの色を追加できます。

$$

$$（R_1、G_1、B_1）+（R_2、G_2、B_2）=（R_1 + R_2、G_1 + G_2、B_1 + B_2）$$

たとえば、赤みがかった紫がある場合

$$

$$（252、0、66）$$

そして、まったく同じ色合いにしたいが、3倍の明るさにしたいので、各チャンネルに $$$1 \ 3ドル以$ そして得る $$$（84、0、22）$ 。 赤を組み合わせたい場合 $$$（255、0、0）$ と緑 $$$（0、255、0）$ 次に、チャネルを追加して取得します $$$（255、255、0）$ それは黄色です。



気配りのある読者は、このような操作では、たとえば明るさを2倍にすることで、誤った値を取得できると言うことができます。 $$$（192、64、32）$ 、色の範囲外のRの値を取得します。 255に等しい255より大きい値、および0に等しい0より小さい値を検討します。これは、シャッター速度が高すぎるまたは低すぎる写真を撮影する場合とほぼ同じです。完全に黒または完全に白の領域が表示されます。

シーン

Canvasは、すべてをレンダリングする抽象概念です。 何をレンダリングしますか？ 別の抽象化はシーンです。



シーンは、レンダリングする必要があるオブジェクトのコレクションです。 空の空間にぶら下がっている唯一の球体（これから始めます）から、鬼の鼻の内部の信じられないほど詳細なモデルまで、何でも構いません。



シーン内のオブジェクトについて話すには、座標系が必要です。 どれでも選択できますが、私たちの目的に役立つものをピックアップします。 Y軸は上に向けられます。 X軸とZ軸は水平です。 つまり、XZ平面が「床」になり、XYとYZが垂直の「壁」になります。



ここでは「物理」オブジェクトについて説明しているので、測定の単位を選択する必要があります。 それらは任意でも構いませんが、シーンに表示されるものに強く依存します。 「1」は、円をモデル化する場合は1ミリメートル、太陽系をモデル化する場合は1天文単位にすることができます。 幸いなことに、次のどれもユニットに依存していないため、単純にそれらを無視します。 均一性を維持する限り（つまり、「1」はシーン全体で常に同じことを意味します）、すべてが正常に機能します。

パートI：レイトレーシング

あなたがエキゾチックな場所にいて、素晴らしい景色を楽しんでいると想像してください。とても素晴らしいので、写真に写すだけです。





スイスの風景



紙とマーカーはありますが、芸術的な才能はまったくありません。 すべてが失われましたか？



必ずしもそうではありません。 才能はないかもしれませんが、方法論があります。



あなたは最も明白なことをすることができます：昆虫のネットを取り、スティックにフレームを取り付けることによって長方形のフレームにそれを置きます。 次に、このグリッドを通して風景を見て、最適な角度を選択し、正確に同じ視点を得るために頭が正確にあるべき場所に別のスティックを置きます。



描画を開始していませんが、少なくとも、固定された視点と、風景が見える固定されたフレームがあります。 さらに、この固定フレームは小さな正方形に分割されます。 そして今、私たちは系統的な部分に進みます。 昆虫の網と同じ数の正方形の紙にグリッドを描きます。 次に、グリッドの左上の正方形を見てください。 どんな色が支配的ですか？ スカイブルー。 したがって、紙の左上の正方形を空色で描画します。 各正方形について同じことを繰り返し、窓から見えるかのように、すぐに風景のかなり良い画像を取得します。





大まかなランドスケープ近似



考えてみると、コンピューターは本質的に非常に系統的な機械であり、芸術的な才能はまったくありません。 紙の上の正方形を画面上のピクセルに置き換えると、次のようにシーンをレンダリングするプロセスを説明できます。

 キャンバスの各ピクセルについて
    希望の色で塗りつぶします。 

とても簡単です！



ただし、このようなコードは抽象的すぎて、コンピューターに直接実装することはできません。 したがって、詳細をもう少し詳しく説明します。

 目とフレームを適切な場所に配置する
キャンバスの各ピクセルについて
    このピクセルに対応するグリッドの正方形を決定します
    この正方形を通して見える色を定義します。
    この色でピクセルを塗りつぶします。 

これはまだ抽象的ですが、すでにアルゴリズムのように見え始めています。 驚いたことに、これはレイトレーシングアルゴリズム全体の高レベルの説明です。 はい、すべてがとても簡単です。



もちろん、悪魔は詳細にあります。 次の章では、これらすべての手順を詳しく見ていきます。

レイトレーシングの基本

コンピューターグラフィックスで最も興味深いものの1つ（そしておそらく最も興味深いもの）は、グラフィックスを画面にレンダリングすることです。 できるだけ早く開始するために、まず画面に何かを表示するためにいくつかの単純化を行います。 もちろん、このような単純化は、可能なアクションの制限を暗示していますが、以降の章ではこれらの制限を段階的に取り除きます。



まず、視点が固定されていると仮定します。 視点は、私たちの類推で目が位置する場所であり、通常はカメラの位置と呼ばれます 。 彼に電話しましょう $$$O =（O_x、O_y、O_z）$ 。 カメラは座標系の先頭にあると仮定します。 $$$O =（0、0、0）$ 。



第二に、カメラの向きも固定されている、つまり、カメラは常に同じ場所に向けられていると仮定します。 正の軸Zに沿って下を向いており、正の軸Yが上を向き、正の軸Xが右にあると仮定します。







カメラの位置と向きが修正されました。 しかし、私たちが提案したアナロジーからの「フレーム」はまだなく、それを通してシーンを見ています。 フレームには寸法があると仮定します $$$V_w$ そして $$$V_h$ 、カメラの位置に対して正面にあります（つまり、垂直 $$$\ vec {Z _ +}$ ）そして距離がある $$$d$ 、その側面はX軸とY軸に平行であり、 $$$\ vec {Z _ +}$ 。 説明は複雑に見えますが、実際にはすべてが非常に単純です。







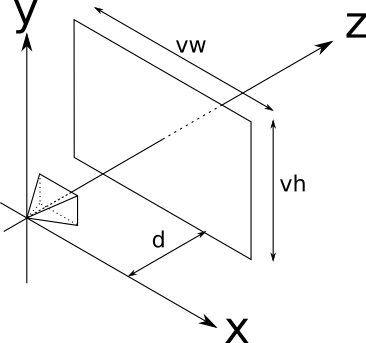
ワールドへのウィンドウとなるこの長方形は、 ビューポートと呼ばれます。 本質的に、ビューポートを通して見えるすべてをキャンバスに描画します。 ビューポートのサイズとカメラまでの距離によって、 視野または略してFOVと呼ばれるカメラからの視野角が決まることが重要です。 人間では、水平視野はほぼ $$$180 ^ \ circ$ ただし、そのほとんどは、奥行き感のない曖昧な周辺視野です。 一般に、信頼できる画像はFOVを使用して取得されます $$$60 ^ \ circ$ 垂直および水平方向; これは尋ねることによって達成することができます $$$V_w = V_h = d = 1$ 。



前のセクションで示した「アルゴリズム」に戻って、そのステップを数字で示します。

 目とフレームを正しい場所に置きます（1）
キャンバスの各ピクセルについて
    このピクセルに対応するグリッドの正方形を決定します（2）
    この正方形を通して見える色を定義します（3）
    この色でピクセルを塗りつぶします（4） 

すでにステップ1を完了しています（または、より正確には、しばらくの間それを取り除きました）。ステップ4は簡単です（canvas.PutPixel(x, y, color)



）。ステップ2を簡単に見てから、ステップ3を実装するためのより複雑な方法に焦点を当てましょう。

キャンバスからビューポートへ

ステップ2では、「このピクセルに対応するグリッドの正方形を決定する」必要があります。キャンバス上のピクセル座標を知っています（すべてを描画します）-それらを呼び出しましょう$$$C_x$ そして $$$C_y$ 。ビューポートの配置がいかに便利であるかに注目してください。その軸はキャンバスの軸の方向に対応し、その中心はビューポートの中心に対応します。つまり、スケールを変更するだけで、キャンバスの座標から空間の座標に移動できます！

$$

$$V_x = C_x {V_w \over C_w}$$

$$

$$V_y = C_y {V_h \over C_h}$$

別の微妙な点があります。ビューポートは2次元ですが、3次元空間に埋め込まれています。カメラから距離dにあることを示しました。定義により、この平面（投影面と呼ばれる）の各点$$$z = d$ 。 だから

$$

$$V_z = d$$

これで手順2が完了しました。各ピクセルについて $$（C x、C y）キャンバスのビューポートの対応する点を決定できます$(C_x, C_y)$$$$(V_x, V_y, V_z)$ 。 ステップ3では、光が通過する色を決定する必要があります $$（V x、V y、V z）カメラビューの観点から$(V_x, V_y, V_z)$$$$(O_x, O_y, O_z)$ 。

光線をたどる

そのため、光はどの色を介して届きますか $$（O x、O y、O z）通過後$(O_x, O_y, O_z)$$$$(V_x, V_y, V_z)$ ？



現実の世界では、光は光源（太陽、電球など）から来て、いくつかのオブジェクトから反射され、最終的に私たちの目に届きます。シミュレートされた光源から放出される各光子の経路をシミュレートすることはできますが、信じられないほど時間がかかります（注：結果は驚くべきものです。この手法は、光子追跡または光子分布と呼ばれます。 。何百万もの光子をシミュレートするだけでなく、表示ウィンドウを通過した後も$$（O x、O y、O z）はそれらのほんの一部にしか到達しません。代わりに、レイを「逆順」でトレースします。カメラにあるレイから開始し、ビューポートのポイントを通過し、シーン内のオブジェクトと衝突するまで移動します。このオブジェクトは、表示ウィンドウのこのポイントを通してカメラから「表示」されます。つまり、最初の近似として、このオブジェクトの色を単に「この点を通過する光の色」と見なします。ここで必要な方程式はわずかです。$(O_x, O_y, O_z)$

光線方程式

この目的のために光線を表す最良の方法は、パラメトリック方程式を使用することです。光線がOを通過し、その方向（OからV）を知っているので、光線の任意の点Pを次のように表現できます。

$$

$$P = O + t(V - O)$$

ここで、tは任意の実数です。



示しましょう$$（V - O ）、つまり、ビームの方向$(V - O)$$$$\vec{D}$ ; 方程式は単純な形を取ります

$$

$$P = O + t\vec{D}$$

これについては、線形代数で詳しく読むことができます。直感的に、開始点から開始してビームの方向の倍数に進むと、常にビームに沿って移動します。

球方程式

次に、光線が何かと衝突できるように、シーンにオブジェクトを追加する必要があります。任意の幾何学的プリミティブをシーンのビルディングブロックとして選択できます。レイトレーシングの場合、数学的な操作の最も単純なプリミティブは球体です。



球体とは何ですか？球体は、固定点（球体の中心と呼ばれる）から一定の距離（球体の半径と呼ばれる）にある点の集合です。定義から判断すると、球体は中空です。Cが球の中心であり、rが球の半径である場合、球の表面上の点Pは次の方程式を満たします。

$$

$$distance(P, C) = r$$

この方程式を少し試してみましょう。PとCの間の距離は、PからCへのベクトルの長さです。

$$

$$|P - C| = r$$

ベクトルの長さは、それ自体のスカラー積の平方根です。

$$

$$\sqrt{\langle P - C, P - C \rangle} = r$$

そして、平方根を取り除くために、

$$

$$\langle P - C, P - C \rangle = r^2$$

レイは球に出会う

これで2つの方程式ができました。1つは球の点を記述し、もう1つは光線の点を記述します。

$$

$$\langle P - C, P - C \rangle = r^2$$

$$

$$P = O + t\vec{D}$$

光線が球に当たる点Pは、光線の点と球の表面上の点の両方であるため、両方の方程式を同時に満たす必要があります。これらの方程式の唯一の変数はパラメーターtであることに注意してください。O、$$→ D、C、およびrが与えられ、Pは見つける必要があるポイントです。Pは両方の方程式で同じポイントであるため、最初のPを2番目のPの式に置き換えることができます。それは私たちに与えます$\vec{D}$

$$

$$\langle O + t\vec{D} - C, O + t\vec{D} - C \rangle = r^2$$

tのどの値がこの方程式を満たしますか？



現在の形式では、方程式はやや面倒です。それを変換して、そこから何が得られるかを見てみましょう。



まず、$$$\vec{OC} = O - C$ 。 方程式は次のように書くことができます

$$

$$\langle \vec{OC} + t\vec{D}, \vec{OC} + t\vec{D} \rangle = r^2$$

次に、分布を使用して、スカラー積をコンポーネントに分解します。

$$

$$\langle \vec{OC} + t\vec{D}, \vec{OC} \rangle + \langle \vec{OC} + t\vec{D}, t\vec{D} \rangle = r^2$$

$$

$$\langle \vec{OC}, \vec{OC} \rangle + \langle t\vec{D}, \vec{OC} \rangle + \langle \vec{OC}, t\vec{D} \rangle + \langle t\vec{D}, t\vec{D} \rangle = r^2$$

少し変換すると、

$$

$$\langle t\vec{D}, t\vec{D} \rangle + 2\langle \vec{OC}, t\vec{D} \rangle + \langle \vec{OC}, \vec{OC} \rangle = r^2$$

スカラー積からパラメーターtを移動し、 $$方程式の別の部分の r 2を取得します。$r^2$

$$

$$t^2 \langle \vec{D}, \vec{D} \rangle + t(2\langle \vec{OC}, \vec{D} \rangle) + \langle \vec{OC}, \vec{OC} \rangle - r^2 = 0$$

かさばらずになりましたか？2つのベクトルのスカラー積は実数であるため、括弧内の各項は実数であることに注意してください。それらを名前で表すと、もっとなじみのあるものが得られます。

$$

$$k_1 = \langle \vec{D}, \vec{D} \rangle$$

$$

$$k_2 = 2\langle \vec{OC}, \vec{D} \rangle$$

$$

$$k_3 = \langle \vec{OC}, \vec{OC} \rangle - r^2$$

$$

$$k_1t^2 + k_2t + k_3 = 0$$

これは古き良き二次方程式に他なりません。その解は、光線が球と交差するパラメーターtの値を提供します。

$$

$$\{ t_1, t_2 \} = {{-k_2 \pm \sqrt{ {k_2}^2 -4k_1k_3} \over {2k_1}}}$$

幸いなことに、これは幾何学的に理にかなっています。覚えているように、判別式の値に応じて、二次方程式には解がなく、1つの二重解または2つの異なる解がある場合があります。$$${k_2}^2 -4k_1k_3$ 。これは、光線が球を交差せず、光線が球に接触し、光線が球に出入りする場合に正確に対応します：







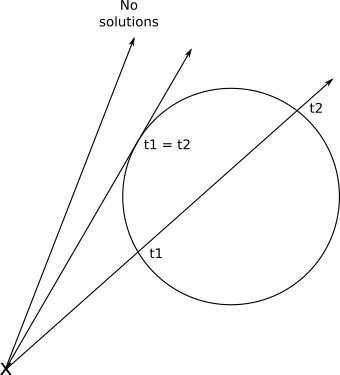
tの値を取得して光線の方程式に挿入すると、このtの値に対応する交点Pを取得します

最初の領域のレンダリング

要約すると、キャンバス上の各ピクセルについて、ビューポート内の対応するポイントを計算できます。カメラの位置がわかれば、カメラから来て表示ウィンドウの特定のポイントを通過するビームの方程式を表現できます。球がある場合、光線がこの球と交差する点を計算できます。



つまり、光線と各球の交点を計算し、カメラに最も近いポイントを保存し、キャンバス上のピクセルを適切な色でペイントするだけです。最初の領域をレンダリングする準備がほぼ整いました！



ただし、パラメータtには特別な注意を払う必要があります。ビーム方程式に戻る：

$$

$$P = O + t(V - O)$$

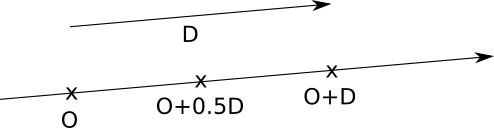
開始点と光線の方向は一定であり、実数のセットでtが変化するため、この光線上のすべての点Pを取得します。ことに注意してください$$t = 0が得られます$t = 0$$$P = O、および$P = O$$$T = 1、我々が得ます$t = 1$$$$P = V$ 。負の数を使用すると、反対方向、つまりカメラの後ろにポイントが得られます。つまり、パラメーター領域を3つの部分に分割できます。

$$$t < 0$	カメラの後ろ
$$$0 \le t \le 1$	カメラと投影面の間
$$$t > 1$	シーン

パラメーター領域の図を次に示します。





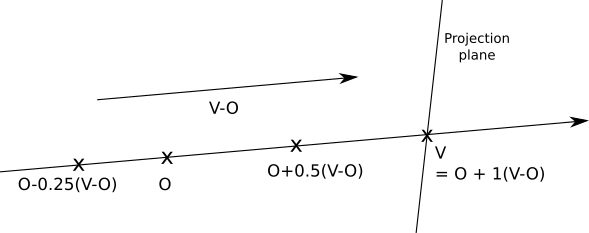
交差式には、球体がカメラの前にある必要があることを示すものがないことに注意してください。方程式は、問題なくカメラの後ろの交差点の解決策を提供します。明らかに、これは必要ありません。したがって、次の場合はすべての決定を無視する必要があります$$$t < 0$ 。 追加の数学的困難を回避するために、ソリューションを制限します $$t > 1、つまり、投影面を超えるすべてのものをレンダリングします。一方、tの値に上限を設定する必要はありません。カメラの前にあるオブジェクトをどれだけ遠くまで見てみたいと思います。後の段階で光線の長さを制限するので、この形式を追加し、tを上限値に制限する必要があります$t > 1$



$$+ ∞（注：無限大を直接指定できない言語では、非常に大きな数で十分です。）これで、擬似コードで行ったすべてを形式化できます。一般的なケースでは、コードが必要なデータにアクセスできると想定するため、最も必要なものを除き、パラメーターを明示的に渡しません。mainメソッドは次のようになります。$+\infty$

 O = <0、0、0>
[-Cw / 2、Cw / 2]のxの場合{
    [-Ch / 2、Ch / 2]のyの場合{
        D = CanvasToViewport（x、y）
        color = TraceRay（O、D、1、inf）
        canvas.PutPixel（x、y、色）
     }
 } 

機能はCanvasToViewport



非常に簡単です。

 CanvasToViewport（x、y）{
    return（x * Vw / Cw、y * Vh / Ch、d）
 } 

このコードd



では、これは投影面までの距離です。



このメソッドTraceRay



は、光線と各球の交差を計算し、必要な間隔tにある最も近い交差点での球の色を返します。

 TraceRay（O、D、t_min、t_max）{
    最も近いt = inf
    nearest_sphere = NULL
    scene.Spheres {の球の場合
        t1、t2 = IntersectRaySphere（O、D、球体）
        [t_min、t_max]のt1およびt1 <closest_tの場合
            最も近いt = t1
            最も近い球体=球体
        [t_min、t_max]のt2およびt2 <closest_tの場合
            最も近いt = t2
            最も近い球体=球体
     }
    nearest_sphere == NULLの場合
        BACKGROUND_COLORを返します
    nearest_sphere.colorを返します
 } 

O



このコードでは、これがビームの開始点です。原点にあるカメラから光線を放出しますが、後の段階で他の場所に配置できるため、この値はパラメーターである必要があります。同じことがt_min



とにも当てはまりますt_max



。



光線が球と交差しない場合でも、色を返す必要があります。ほとんどの例では、このために白を選択しました。



そして最後にIntersectRaySphere



、二次方程式を解くだけです：

 IntersectRaySphere（O、D、sphere）{
    C = sphere.center
    r = sphere.radius
    oc = O-C

    k1 =ドット（D、D）
    k2 = 2 *ドット（OC、D）
    k3 =ドット（OC、OC）-r * r

    判別式= k2 * k2-4 * k1 * k3
    判別<0の場合：
        inf、infを返す

    t1 =（-k2 + sqrt（判別式））/（2 * k1）
    t2 =（-k2-sqrt（判別式））/（2 * k1）
    t1、t2を返す
 } 

非常に単純なシーンを定義しましょう：シーン







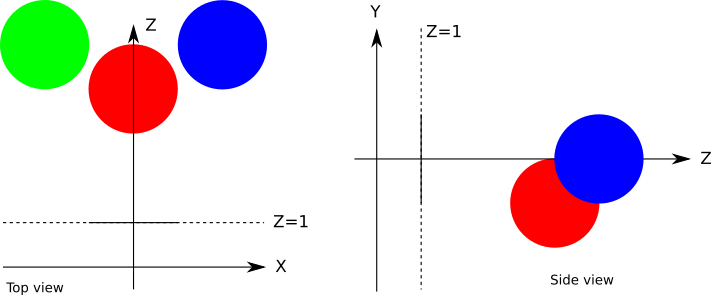
の擬似言語では、次のように設定されます。

 viewport_size = 1 x 1
projection_plane_d = 1
sphere {
    center =（0、-1、3）
    半径= 1
    color =（255、0、0）＃赤
 }
sphere {
    中央=（2、0、4）
    半径= 1
    color =（0、0、255）＃青
 }
sphere {
    中央=（-2、0、4）
    半径= 1
    color =（0、255、0）＃緑
 } 

次に、このシーンのアルゴリズムを実行すると、レイトレーシングによって得られた信じられないほどのシーンのビューが最終的に報われます。







ソースコードと作業デモ>>



これは少し残念です。反射、影、美しい外観はどこにありますか？まだ始まったばかりなので、これをすべて取得します。しかし、これは良い出発点です-球体は円のように見え、猫のように見える場合よりも優れています。人がオブジェクトの形状、つまり光と相互作用する方法を決定できる重要なコンポーネントを見逃しているため、球体のようには見えません。

照明

シーンレンダリングに「リアリズム」を追加する最初のステップは、照明をシミュレートすることです。照明はめちゃくちゃ複雑なトピックなので、私たちの目的に十分な非常に単純化されたモデルを紹介します。このモデルの一部は物理モデルにさらに近いものではなく、高速で見栄えが良いです。



私たちの生活を楽にするいくつかの単純化された仮定から始めます。



まず、すべての照明が白色であることを発表します。これにより、光源の明るさと呼ばれる単一の実数iで光源を特徴付けることができます。カラー照明のシミュレーションはそれほど複雑ではありません（チャネルごとに1つ、3つの輝度値のみが必要です。また、チャネルごとにすべての色と照明を計算する必要があります）。



次に、大気を取り除きます。これは、範囲に関係なく、照明の明るさが低下しないことを意味します。距離に応じてライトの明るさを暗くすることも実装するのはそれほど難しくありませんが、わかりやすくするためにここではスキップします。

光源

光はどこかから来なければなりません。このセクションでは、3種類の光源を定義します。

ポイントソース

点光源は、その位置と呼ばれる空間内の固定点から光を放出します。光はすべての方向に均等に放出されます。それが全方向照明とも呼ばれる理由です。したがって、点光源は、その位置と明るさによって完全に特徴付けられます。



白熱灯は、1つの近似値が照明の点光源である現実世界の良い例です。白熱灯は1つのポイントから光を放射せず、完全に全方向性ではありませんが、近似は非常に良好です。



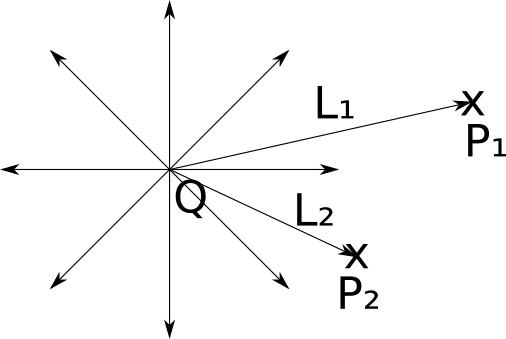
ベクトルを設定しましょう$$→シーン内のポイントPから光源Qへの方向としての L。このベクトルはライトベクトルと呼ばれ、単に$\vec{L}$$$$Q - P$ 。 Qは固定されており、Pはシーン内の任意のポイントにできるため、一般的な場合 $$→ Lは、シーンの各ポイントで異なります。$\vec{L}$

指向性ソース

点光源が白熱灯の適切な近似である場合、太陽の近似として役立つものは何ですか？



これは難しい質問であり、答えは何をレンダリングしたいかによって異なります。



太陽系の規模では、太陽はほぼ点光源と見なすことができます。最終的に、ある点から（かなり大きいとはいえ）光を放射し、すべての方向に放射します。つまり、両方の要件に適合します。



ただし、シーン内でアクションが地球上で発生する場合、これはあまり適切な近似ではありません。太陽は非常に離れているため、各光線は実際には同じ方向になります（注：この近似値は都市スケールで保持されますが、実際には遠くではありません。実際、古代ギリシャ人は異なる方向に基づいて驚くほど正確に地球の半径を計算できましたさまざまな場所の日光。）。シーンから遠く離れた点光源を使用してこれを近似することは可能ですが、この距離とシーン内のオブジェクト間の距離は大きさが非常に異なるため、数値の精度に誤差が生じる可能性があります。



そのような場合、指向性光源を定義します。。点光源と同様に、指向性光源には明るさがありますが、それらとは異なり、位置はありません。代わりに、彼は方向を持っています。特定の方向に輝く無限遠の点光源として認識することができます。



点光源の場合、新しい光ベクトルを計算する必要があります$$→シーンの各ポイントPに対して L、ただしこの場合$\vec{L}$$$→ Lが与えられます。太陽と地球のあるシーンで$\vec{L}$$$→ Lは等しくなります$\vec{L}$$$$(\text{ }) - (\text{ })$ 。

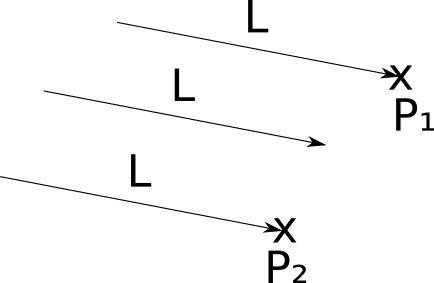
アンビエント照明

実際の照明は、点光源または指向性光源としてモデル化できますか？ほとんど常にそうです（ただし、これは必ずしも単純ではありません。ゾーン照明（ディフューザーの背後にある光源を想像してください）は、その表面上の多くの点光源によって近似できますが、これは難しく、計算コストが高く、結果は理想的ではありません）。これらの2種類のソースは、私たちの目的に十分ですか？残念ながら、ありません。



月で何が起こっているか想像してみてください。近くにある唯一の重要な光源は太陽です。つまり、太陽に対する月の「前半分」はすべての照明を受け、「後ろ半分」は完全な暗闇の中にあります。私たちはこれを地球上のさまざまな角度から見ており、この効果は私たちが月の「位相」と呼ぶものを作り出します。



しかし、地球上の状況はわずかに異なります。光源から直接光を受けないポイントでさえ、完全に暗闇ではありません（テーブルの下の床を見てください）。光源の「ビュー」が何かによって遮られている場合、光線はどのようにしてこれらのポイントに到達しますか？カラーモデル



セクションで述べたように光がオブジェクトに当たると、その一部は吸収されますが、残りはシーン内で散乱します。これは、光が光源からだけでなく、光源からそれを受け取り、それを散乱させる他のオブジェクトからも来ることを意味します。しかし、なぜこれにこだわるのでしょうか？拡散した照明は、他のオブジェクトに当てられ、その一部が吸収され、一部が再びシーンに散らばります。反射するたびに、光は明るさの一部を失いますが、理論的には無限に続けることができます（注：光は量子的性質であるため、実際にはそうではありませんが、これに十分に近いです）。



これは、各オブジェクトを照明の光源と見なす必要があることを意味します。。ご想像のとおり、これによりモデルの複雑さが大幅に増加するため、この方法は使用しません（ただし、少なくともグローバルイルミネーションをグーグル検索して美しい画像を見ることができます）。



ただし、各オブジェクトを直接照らしたり、完全に暗くしたりすることは望みません（太陽系のモデルをレンダリングしない限り）。この障壁を克服するために、明るさのみによって特徴付けられる、アンビエントライトと呼ばれる3番目のタイプの光源を定義します。シーンのあらゆるポイントに照明の無条件の寄与をもたらすと考えられています。これは、光源とシーンサーフェス間の非常に複雑な相互作用を非常に強力に単純化したものですが、機能します。

シングルポイント照明

一般に、シーンには、アンビエント照明の1つのソース（アンビエント照明には輝度値のみがあり、それらの任意の数がアンビエント照明の単一のソースに簡単に結合されるため）と、任意の数のポイントおよび方向ソースがあります。



ポイントの照度を計算するには、各光源が導入する光量を計算し、それらを加算して、ポイントが受け取る総光量を表す1つの数値を取得するだけです。次に、このポイントの表面の色にこの数値を掛けて、適切に照明された色を取得します。



それで、方向を持つ光線が$$→有向または点光源からの Lは、シーン内のあるオブジェクトの点Pに落ちますか？直観的には、オブジェクトが光でどのように動作するかに応じて、オブジェクトを「マット」と「ブリリアント」の2つの一般的なクラスに分けることができます。私たちの周りのほとんどのオブジェクトは「不透明」と見なすことができるので、それらから始めます。$\vec{L}$

拡散散乱

光線が不透明なオブジェクトに当たると、顕微鏡レベルでの表面の粗さにより、光線はすべての方向に均一にシーンに反射されます。つまり、「拡散」（「拡散」）反射が得られます。



これを確認するために、壁などの不透明なオブジェクトを注意深く見てください。壁に沿って移動しても、色は変わりません。つまり、オブジェクトから反射される光は、オブジェクトを見る場所に関係なく同じです。



一方、反射光の量は、光線と表面の間の角度に依存します。直観的には、これは理解できます-ビームによって転送されるエネルギーは、角度に応じて、より小さなまたはより大きな表面に分散する必要があります。つまり、シーンに反映される単位面積あたりのエネルギーはそれぞれ高くまたは低くなります。







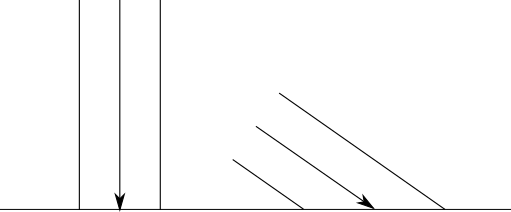
これを数学的に表現するために、その法線ベクトルによって表面の向きを特徴付けましょう。法線ベクトル、または単に「法線」は、ある点で表面に垂直なベクトルです。また、単位ベクトルです。つまり、長さは1です。このベクトルを呼び出します。$$$\vec{N}$ 。

拡散反射モデリング

だから、方向を持つ光線 $$→ Lと明るさ$\vec{L}$$$法線で表面に落ちる$I$$$$\vec{N}$ 。 どの部分 $$私はシーンを関数として反映しました$I$$$$I$ 、 $$$\vec{N}$ そして $$$\vec{L}$ ？



幾何学的な類推のために、光の明るさをビームの「幅」として想像してみましょう。そのエネルギーは、サイズごとに表面に分布します$$$A$ 。 いつ $$$\vec{N}$ そして $$→ Lには1つの方向があります。つまり、ビームは表面に垂直です。$\vec{L}$$$I = A。これは、単位面積あたりの反射エネルギーが単位面積あたりの入射エネルギーに等しいことを意味します。<$I = A$$$${I \over A} = 1$ 。 一方、角度が $$$\vec{L}$ そして $$→ N個のアプローチ$\vec{N}$$$$90^\circ$ 、 $$Aが近づいています$A$$$∞、つまり、単位面積あたりのエネルギーは0に近づきます。$\infty$$$$\lim_{A \to \infty} {I \over A} = 0$ 。しかし、間に何が起こるのでしょうか？



この状況を下の図に示します。知ってる$$$\vec{N}$ 、 $$$\vec{L}$ そして $$$P$ ; 角度を追加しました $$$\ alpha$ そして $$\ベータだけでなく、ポイント$\ベータ$$$$Q$ 、 $$$\vec{R}$ そして $$Sこのスキームに関連する記録を簡単にします。技術的に光線には幅がないため、すべてが無限に小さな平らな表面領域で発生すると想定します。たとえそれが球体の表面であっても、地球が小さなスケールで平らに見えるように、考慮中の領域は無限に小さく、球体のサイズに対してほぼ平らです。幅のある光のビーム$S$











$$ある地点で水面に落ちる$I$$$斜めの P$P$$$$\ベータ$ 。 ポイントで正常 $$Pは等しい$P$$$→ N、およびビームによって運ばれるエネルギーは$\vec{N}$$$$A$ 。 計算する必要があります $$${I \over A}$ 。



検討します $$S Rビームの「幅」。定義により、垂直です$SR$$$→ L、これも方向です$\vec{L}$$$$PQ$ 。 だから $$$PQ$ そして $$Q Rは直角を形成し、回転します$QR$$$P Q Rを直角三角形にします。コーナーの1つ$PQR$



$$P Q Rは次と等しい$PQR$$$90 ∘、およびその他-$90^\circ$$$$\ベータ$ 。 次に、3番目の角度は $$$90^\circ - \beta$ 。 しかし、それに注意する必要があります $$$\vec{N}$ そして $$P Rはまた直角を形成します。$PR$$$α + βも$\alpha + \beta$$$$90^\circ$ 。 だから $$$\widehat{QRP} = \alpha$ ：







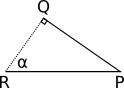
三角形を見てみましょう $$$PQR$ 。 その角度は等しい $$$\ alpha$ 、 $$$\ベータ$ そして $$$90^\circ$ 。 パーティー $$Q Rは次と等しい$QR$$$私は2、および側面$I \over 2$$$P Rは次と等しい$PR$$$$A \over 2$ 。



そして今...三角法は急いで助けになります！定義により$$$cos(\alpha) = {QR \over PR}$ ; 取り替える $$$QR$ に $$$I \over 2$ 、そして $$$PR$ に $$A2、そして我々は得る$A \over 2$

$$

$$cos(\alpha) = { {I \over 2} \over {A \over 2} }$$

に変換されるもの

$$

$$cos(\alpha) = {I \over A}$$

ほぼ完了です。 $$ a l p h aは、$\ alpha$$$$\vec{N}$ そして $$→ L、つまり$\vec{L}$$$c o s （α ）は、$cos(\alpha)$

$$

$$cos(\alpha) = {{\langle \vec{N}, \vec{L} \rangle} \over {|\vec{N}||\vec{L}|}}$$

そして最後に

$$

$${I \over A} = {{\langle \vec{N}, \vec{L} \rangle} \over {|\vec{N}||\vec{L}|}}$$

そのため、光の反射部分と、表面の法線と光の方向との間の角度を結ぶ非常に簡単な方程式を得ました。



より大きい角度で注意してください$$$90^\circ$ 価値 $$c o s （α ）は負になります。この値を使用することをためらわなければ、光を差し引く光源になります。これには物理的な意味はありません。角度が大きい$cos(\alpha)$$$90 ∘光が実際に到達したことを単に意味後面、および照明ポイントのカバレッジに寄与しません。つまり、$90^\circ$$$c o s （α ）は負になり、それから等しいと考える$cos(\alpha)$$$$0$ 。

拡散反射方程式

これで、ポイントが受け取る光の総量を計算する方程式を定式化できます $$通常の P$P$$$→周囲の明るさがあるシーンの N$\vec{N}$$$$I_A$ そして $$Nポイントまたは輝度で指向性光$n$$$I nおよびライトベクトル$I_n$$$→ L n既知（有向光源の場合）、またはPに対して計算（点光源の場合）：$\vec{L_n}$

$$

$$I_P = I_A + \sum_{i = 1}^{n} I_i {{\langle \vec{N}, \vec{L_i} \rangle} \over {|\vec{N}||\vec{L_i}|}}$$

メンバーが $$⟨ → N、→ L iが ⟩ < 0は、光ポイントに追加されるべきではありません。$\langle \vec{N}, \vec{L_i} \rangle < 0$

通常の球

ここで唯一の些細な事が欠けています：法線はどこから来ますか？



この質問は、記事の第2部で見るように、見かけよりもはるかに複雑です。幸いなことに、分析している場合には、非常に簡単な解決策があります。球の任意の点の法線ベクトルは、球の中心を通る線上にあります。つまり、球体の中心が$$C、次に点の法線の方向$C$$$$P$ 等しい $$$P - C$ ：







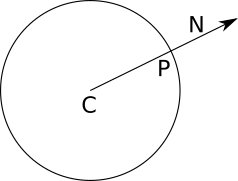
「普通」ではなく「普通の方向」と書いたのはなぜですか？表面に対する垂直性に加えて、法線は単位ベクトルでなければなりません。これは、球の半径が等しい場合に当てはまります$$1、これは常に正しいとは限りません。法線自体を計算するには、ベクトルをその長さで除算して、長さを取得する必要があります$1$$$$1$ ：

$$

$$\vec{N} = {{P - C} \over {|P - C|}}$$

上記のライティング方程式には、 $$| → N | しかし、良いアプローチは「真の」法線を作成することです。これにより、今後の作業が簡素化されます。$|\vec{N}|$

拡散反射レンダリング

これらすべてを擬似コードに変換しましょう。まず、シーンにいくつかの光源を追加しましょう。

 ライト{
    タイプ=アンビエント
    強度= 0.2
 }
ライト{
    タイプ=ポイント
    強度= 0.6
    位置=（2、1、0）
 }
ライト{
    タイプ=方向
    強度= 0.2
    方向=（1、4、4）
 } 

明るさが便利に積み重なることに注意してください $$1.0は、ライティングの式から、ポイントが1よりも高い光の輝度を持つことはできないためです。これは、「露出が多すぎる」エリアを取得しないことを意味します。ライティングの方程式は、擬似コードに変換するのは非常に簡単です。$1.0$

 ComputeLighting（P、N）{
    i = 0.0
    scene.Lights {
        light.type == ambient {
            i + = light.intensity
        } else {
            light.type ==ポイントの場合
                L = light.position-P
            他に
                L = light.direction

            n_dot_l =ドット（N、L）
            n_dot_l> 0の場合
                i + = light.intensity * n_dot_l /（長さ（N）*長さ（L））
         }
     }
    私を返す
 } 

そして、唯一のことは、左-を使用することComputeLighting



にTraceRay



。球の色を返す文字列を置き換えます

 nearest_sphere.colorを返します 

このスニペットに：

 P = O + nearest_t * D＃交差点の計算
    N = P-nearest_sphere.center＃交差点での球の法線を計算します
    N = N /長さ（N）
    最も近い_sphere.colorを返します* ComputeLighting（P、N） 

楽しみのために、大きな黄色の球体を追加しましょう。

 sphere {
    color =（255、255、0）＃黄色
    中央=（0、-5001,0）
    半径= 5000
 } 

レンダラーを実行すると、見よ-球体がついに球体のように見え始めました！







ソースコードと動作デモ>>



しかし、待ってください。大きな黄色い球体はどのようにして平らな黄色い床に変わりましたか？



これはそうではありませんでした。他の3つと比べて非常に大きく、カメラは非常に近く、平らに見えます。地球上に立つと、地球が平らに見えるように。

滑らかな表面反射

次に、「光沢のある」オブジェクトに注目します。 「マット」オブジェクトとは異なり、「華麗な」オブジェクトは、さまざまな角度から見たときに外観が変化します。



ビリヤードボールを取るか、車を洗うだけです。そのようなオブジェクトでは、光の伝播の特別なパターンが表示されます。通常は、周りを歩くと動くように見える明るい領域があります。マットオブジェクトとは異なり、これらのオブジェクトの表面を認識する方法は、実際には視点によって異なります。



赤いビリヤードボールは2、3歩下がっても赤のままですが、「光沢のある」外観を与える明るい白いスポットは動くようです。これは、新しい効果が拡散反射に代わるものではなく、それを補完することを意味します。



なぜこれが起こっているのですか？マットオブジェクトでこれが起こらない理由から始めましょう。前のセクションで見たように、光線がマットオブジェクトの表面に当たると、光線はすべての方向に均一に散乱してシーンに戻ります。直観的には、これはオブジェクトの表面の不均一性のために発生します。つまり、顕微鏡レベルでは、ランダムな方向を向いた多くの小さな表面のように見え







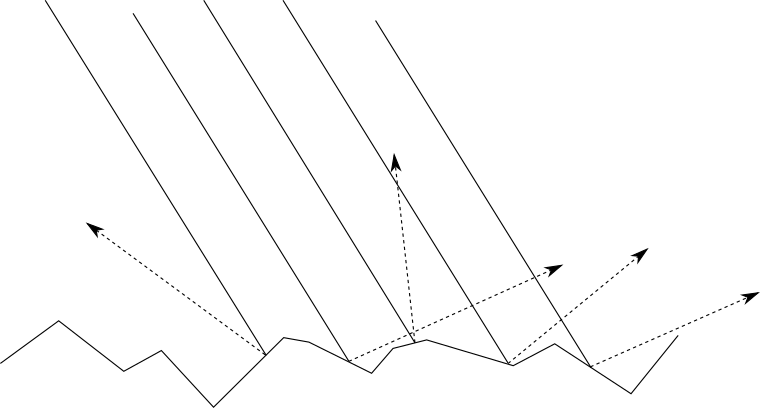
ます。もう1つの極端な例、完全に洗練されたミラーを見てみましょう。光線がミラーに当たると、ミラーの法線に対する入射角に対称な単一方向に反射します。反射光の方向を呼ぶと$$→ Rと私たちは同意します$\vec{R}$$$→ Lは光源を示し、次のような状況になります。「研磨された」表面の程度に応じて、多かれ少なかれ鏡のようです。つまり、「鏡」反射（ラテン語「鏡」からの鏡面反射、つまり「鏡」）を取得します。完全に磨かれた鏡の場合、入射光線$\vec{L}$











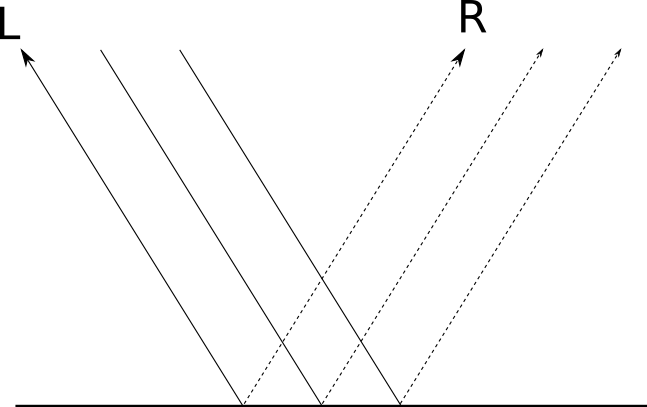
$$→ Lは単一の方向に反映されます$\vec{L}$$$$\vec{R}$ 。 これにより、ミラー内のオブジェクトを明確に見ることができます。入射光線ごとに $$→ Lは唯一の反射ビームです$\vec{L}$$$$\vec{R}$ 。しかし、すべてのオブジェクトが完全に洗練されているわけではありません。ほとんどの光は方向に反射されますが$$→ R、その一部は近くの方向に反映されます$\vec{R}$$$$\vec{R}$ ; に近い $$→ R、この方向により多くの光が反射されます。オブジェクトの「輝き」は、離れるときに反射光がどれだけ速く減少するかを決定します$\vec{R}$$$$\vec{R}$ ：







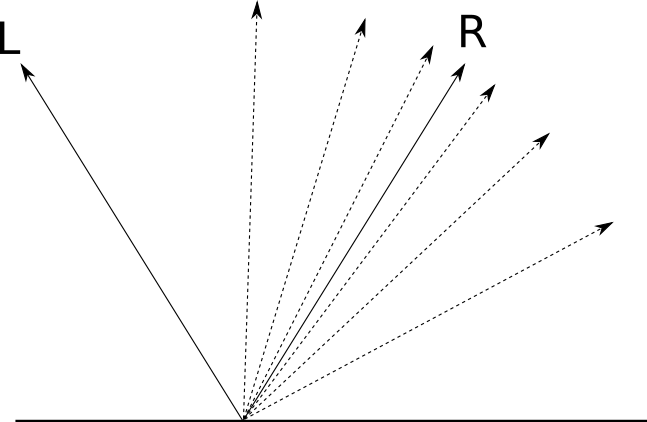
私たちはどのくらいの光を見つけるのに興味があります $$→ Lは視点の方向に反射されます（各点の色を決定するために使用するのは光だからです）。$\vec{L}$もし $$→ Vは、以下を示す「調査ベクトル」です$\vec{V}$$$カメラに P$P$$$ LのPの時間A -との間の角度$\ alpha$$$$\vec{R}$ そして $$→ V、これは私たちが持っているものです：$\vec{V}$







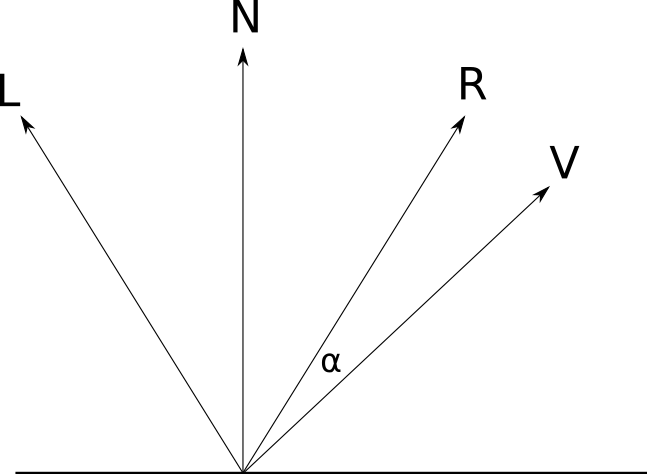
で $$α = 0 ∘全ての光を反射します。$\alpha = 0^\circ$で $$α = 90 ∘光が反射されません。拡散反射と同様に、中間値で何が起こるかを決定する数式が必要です$\alpha = 90^\circ$$$$\ alpha$ 。

ミラー反射のモデリング

すべてのモデルが物理モデルに基づいているわけではないことを先ほど説明したことを覚えていますか？さて、ここにその一例があります。以下に示すモデルは任意ですが、計算が簡単で見栄えが良いため、使用されます。



とりましょう$$$cos(\alpha)$ 。 優れた特性があります。 $$$cos(0) = 1$ 、 $$c o s （± 90 ）= 0で、値は徐々に減少します$cos(\pm 90) = 0$$$$0$ 前に $$非常に美しい曲線に沿った 90：$90$







$$c o s （α ）は、「ミラー」反射機能のすべての要件を満たしているので、使用しないのはなぜですか？しかし、もう1つ詳細がありません。この定式化では、すべてのオブジェクトが等しく輝きます。方程式を変更して異なる光沢度を得る方法は？この光沢は、反射関数が増加するにつれてどれだけ速く減少するかの尺度であることを忘れないでください$cos(\alpha)$







$$$\ alpha$ 。 異なる光度曲線を取得する非常に簡単な方法は、次数を計算することです $$c o s （いくつかの正の指標の α$cos(\alpha$$$$s$ 。 以来 $$0 ≤ C 、O 、S （α ）≤ 1、それは明らかです$0 \le cos(\alpha) \le 1$$$$0 \le cos(\alpha)^s \le 1$ ; それは $$c o s （α ）sは、次とまったく同じように動作します。$cos(\alpha)^s$$$c o s （α、「すでに」のみ。$cos(\alpha$ここに $$異なる値の c o s （α ）s$cos(\alpha)^s$$$$s$ ：







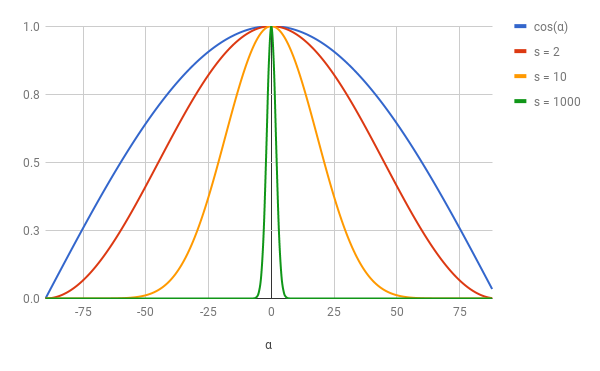
より高い価値 $$s、「すでに」は近傍の関数になります$s$$$0、およびオブジェクトがより輝くように見えます。$0$



$$sは通常、反射インデックスと呼ばれ、表面特性です。モデルは物理的現実に基づいていないため、意味$s$$$sは試行錯誤によってのみ、つまり「自然」に見えるまで値を調整することによってのみ決定できます（注：物理学ベースのモデルを使用するには、2ビーム反射関数（DFOS）を参照してください）。すべて一緒にしましょう。レイ$s$



$$→ Lは点で表面に落ちます$\vec{L}$$$Pは法線$P$$$→ N、および反射指数は$\vec{N}$$$$s$ 。 視線方向に反射される光の量 $$$\vec{V}$ ？



この値は、 $$$cos(\alpha)^s$ どこで $$ a l p h aは、$\ alpha$$$$\vec{V}$ そして $$→ R順番にあり、$\vec{R}$$$→ Lは、比較的反射しました$\vec{L}$$$$\vec{N}$ 。 つまり、最初のステップは計算することです $$$\vec{R}$ から $$$\vec{N}$ そして $$$\vec{L}$ 。



分解できます $$→ Lから2つのベクトル$\vec{L}$$$$\vec{L_P}$ そして $$→ L Nように、$\vec{L_N}$$$$\vec{L} = \vec{L_P} + \vec{L_N}$ どこで $$→ L Nは平行$\vec{L_N}$$$$\vec{N}$ 、そして $$→ L Pは垂直$\vec{L_P}$$$$\vec{N}$ ：







$$→ L Nは投影$\vec{L_N}$$$$\vec{L}$ に $$$\vec{N}$ ; スカラー積の特性に従い、次の事実に基づいて $$| → N | = 1、この投影の長さは$|\vec{N}| = 1$$$$\langle \vec{N}, \vec{L} \rangle$ 。 私たちはそれを決定しました $$→ L Nは平行になります$\vec{L_N}$$$→ N、そう$\vec{N}$$$$\vec{L_N} = \vec{N} \langle \vec{N}, \vec{L} \rangle$ 。



以来 $$→ L = → L P + → L N、すぐに取得できます$\vec{L} = \vec{L_P} + \vec{L_N}$$$$\vec{L_P} = \vec{L} - \vec{L_N} = \vec{L} - \vec{N} \langle \vec{N}, \vec{L} \rangle$ 。



今見て $$$\vec{R}$ ; 対称的だから $$→ L相対$\vec{L}$$$→ N、そのコンポーネント、並列$\vec{N}$$$→ N、同じ$\vec{N}$$$→ L、および垂直成分は成分の反対です$\vec{L}$$$$\vec{L}$ ; それは $$$\vec{R} = \vec{L_N} - \vec{L_P}$ ：







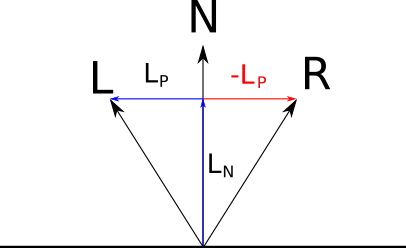
前に取得した式を代入すると、次のようになります

$$

$$\vec{R} = \vec{N} \langle \vec{N}, \vec{L} \rangle - \vec{L} + \vec{N} \langle \vec{N}, \vec{L} \rangle$$

少し簡略化すると、

$$

$$\vec{R} = 2\vec{N} \langle \vec{N}, \vec{L} \rangle - \vec{L}$$

「鏡」反射の価値

これで、「鏡」反射の方程式を書く準備ができました。

$$

$$\vec{R} = 2\vec{N} \langle \vec{N}, \vec{L} \rangle - \vec{L}$$

$$

$$I_S = I_L \left( {{\langle \vec{R}, \vec{V} \rangle} \over {|\vec{R}||\vec{V}|}} \right)^s$$

拡散照明と同様に、 $$c o s （α ）は負の値になる可能性があるため、再度無視しなければなりません。さらに、すべてのオブジェクトが素晴らしいわけではありません。そのようなオブジェクト（これは、$cos(\alpha)$$$S = - 1）一般に「ミラー」の値が算出されません。$s = -1$

鏡像レンダリング

現在作業中の「ミラー」反射をシーンに追加しましょう。まず、シーン自体にいくつかの変更を加えます。

 sphere {
    center =（0、-1、3）
    半径= 1
    color =（255、0、0）＃赤
    鏡面反射= 500＃ブリリアント
 }
sphere {
    中央=（-2、1、3）
    半径= 1
    color =（0、0、255）＃青
    鏡面反射= 500＃ブリリアント
 }
sphere {
    中央=（2、1、3）
    半径= 1
    color =（0、255、0）＃緑
    鏡面反射= 10＃少し華麗
 }
sphere {
    color =（255、255、0）＃黄色
    中央=（0、-5001,0）
    半径= 5000
    鏡面反射= 1000＃非常に素晴らしい
 } 

コードでは、必要にComputeLighting



応じて「ミラーリング」の値を計算し、一般的な照明に追加するように変更する必要があります。今彼が必要とすることに注意してください$$$\vec{V}$ そして $$$s$ ：

 ComputeLighting（P、N、V、s）{
    i = 0.0
    scene.Lights {
        light.type == ambient {
            i + = light.intensity
        } else {
            light.type ==ポイントの場合
                L = light.position-P
            他に
                L = light.direction

            ＃拡散
            n_dot_l =ドット（N、L）
            n_dot_l> 0の場合
                i + = light.intensity * n_dot_l /（長さ（N）*長さ（L））

            ＃ミラーリング
            if s！= -1 {
                R = 2 * N *ドット（N、L）-L
                r_dot_v =ドット（R、V）
                r_dot_v> 0の場合
                    i + = light.intensity * pow（r_dot_v /（長さ（R）*長さ（V））、s）
             }
         }
     }
    私を返す
 } 

最後に、TraceRay



新しいパラメータを渡すように変更する必要がありますComputeLighting



。$$sは明らかです。球体のデータから取得されます。しかし、どうですか$s$$$$\vec{V}$ ？ $$→ Vは、オブジェクトからカメラを指すベクトルです。幸いなことに、カメラからオブジェクトに向けられたベクトルが既にあります-これ$\vec{V}$TraceRay



$$→ D、トレースされた光線の方向！$\vec{D}$それは $$→ Vはただ$\vec{V}$$$$-\vec{D}$ 。



TraceRay



「ミラー」リフレクションを使用した新しいコードを次に示します。

 TraceRay（O、D、t_min、t_max）{
    最も近いt = inf
    nearest_sphere = NULL
    scene.Spheres {の球の場合
        t1、t2 = IntersectRaySphere（O、D、球体）
        [t_min、t_max]のt1およびt1 <closest_tの場合
            最も近いt = t1
            最も近い球体=球体
        [t_min、t_max]のt2およびt2 <closest_tの場合
            最も近いt = t2
            最も近い球体=球体
     }
    nearest_sphere == NULLの場合
        BACKGROUND_COLORを返します

    P = O + nearest_t * D＃交差点の計算
    N = P-nearest_sphere.center＃交差点での球の法線を計算します
    N = N /長さ（N）
    最も近い_sphere.colorを返す* ComputeLighting（P、N、-D、sphere.specular）
 } 

そして、すべてこのジャグリングベクトルについて、当社の報酬：







ソースコードと作業のデモ>>

影

光と物体があるところには、影がなければなりません。それで私たちの影はどこにあるのでしょうか？



より基本的な質問から始めましょう。なぜべきで影も？影は光があるところに現れますが、その光線はオブジェクトに到達できません。パスに別のオブジェクトがあるためです。



前のセクションでは角度とベクトルに関心がありましたが、光源と色付けする必要がある点のみを考慮し、シーンで発生する他のすべてを完全に無視しました-たとえば、邪魔になったオブジェクト。



代わりに、「ポイントとソースの間にオブジェクトがある場合、このソースからの照明を追加する必要はありません」という小さなロジックを追加する必要があります。



次の2つのケースを強調します。







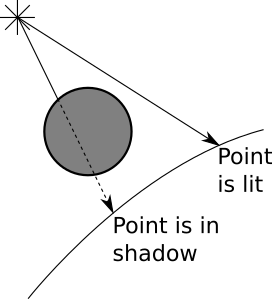
これに必要なツールはすべて揃っているようです。



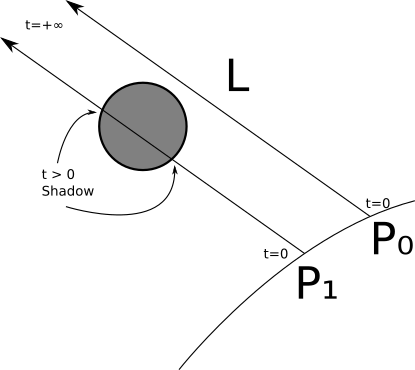
指向性ソースから始めましょう。知ってる$$$P$ ;これが私たちの興味を引くポイントです。知ってる$$$\vec{L}$ ;これは光源の定義の一部です。持っている$$$P$ そして $$→ L、つまり光線を設定できます。$\vec{L}$$$P + t → L。ある点から無限遠の光源まで通過します。この光線は別のオブジェクトと交差しますか？そうでない場合は、ポイントとソースの間に何もありません。つまり、このソースから照明を計算し、それを合計照明に追加できます。交差する場合、このソースを無視します。光線と球体の間の最も近い交差点を計算する方法はすでに知っています。カメラからの光線を追跡するために使用します。再び使用して、光線とシーンの残りの部分との間の最も近い交差を計算できます。ただし、オプションはわずかに異なります。カメラから開始する代わりに、$P + t\vec{L}$







$$$P$ 。 方向が等しくない $$$(V - O)$ 、そして $$$\vec{L}$ 。 そして、私たちはすべての後と交差することに興味があります $$Pから無限の距離。ということです$P$$$$t_{min} = 0$ そして $$$t_{max} = +\infty$ 。







ポイントソースは非常に似た方法で処理できますが、2つの例外があります。まず、設定されていません$$→ Lですが、ソースの位置から計算するのは非常に簡単です。$\vec{L}$$$$P$ 。 第二に、以下から始まる交差点に興味があります $$P、ただしまで$P$$$L（それ以外の場合、光源の背後にあるオブジェクトが影を作成する可能性があります！）; つまり、この場合$L$$$$t_{min} = 0$ そして $$$t_{max} = 1$ 。







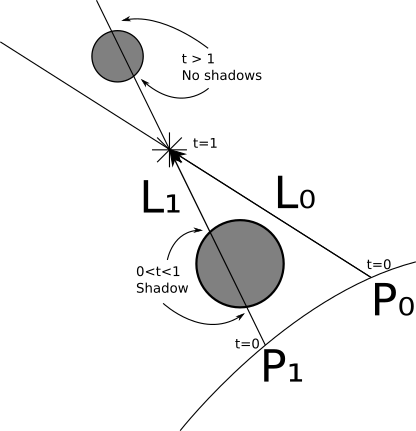
考慮すべき境界線のケースが1つあります。光線を取る$$$P + t\vec{L}$ 。 で始まる交差点を探すと $$t m i n = 0の場合、$t_{min} = 0$$$$P$ で $$t = 0の理由$t = 0$$$Pは実際に球体上にあり、$P$$$$P + 0\vec{L} = P$ ;言い換えれば、各オブジェクトはそれ自身に影を落とします（注：より正確には、オブジェクト全体ではなく、ポイントがそれ自体に影を落とす状況を避けたいです;球体よりも複雑な形状のオブジェクト（つまり、凹面オブジェクト）自体に真の影を落とすことができます！



これを処理する最も簡単な方法は、値の下限を使用することです$$$t$ の代わりに $$0低い値$0$$$$\イプシロン$ 。 幾何学的に、表面から少し離れたところ、つまり、 $$Pではなく正確に$P$$$$P$ 。 つまり、有向ソースの場合、間隔は $$[ ϵ 、+ ∞ ]および点-$[\epsilon, +\infty]$$$$[\epsilon, 1]$ 。

影付きのレンダリング

これを擬似コードに変えましょう。



前のバージョンでTraceRay



は、ビームと球体の最も近い交差点を計算し、次に交差点の照明を計算しました。影を計算するために再び使用するため、最も近い交差点のコードを抽出する必要があります。

 ClosestIntersection（O、D、t_min、t_max）{
    最も近いt = inf
    nearest_sphere = NULL
    scene.Spheres {の球の場合
        t1、t2 = IntersectRaySphere（O、D、球体）
        [t_min、t_max]のt1およびt1 <closest_tの場合
            最も近いt = t1
            最も近い球体=球体
        [t_min、t_max]のt2およびt2 <closest_tの場合
            最も近いt = t2
            最も近い球体=球体
     }
    最も近い_sphere、最も近い_tを返す
 } 

結果TraceRay



ははるかに簡単です：

 TraceRay（O、D、t_min、t_max）{
    nearest_sphere、closest_t = ClosestIntersection（O、D、t_min、t_max）

    nearest_sphere == NULLの場合
        BACKGROUND_COLORを返します

    P = O + nearest_t * D＃交差点の計算
    N = P-nearest_sphere.center＃交差点での球の法線を計算します
    N = N /長さ（N）
    最も近い_sphere.colorを返す* ComputeLighting（P、N、-D、sphere.specular）
 } 

次にComputeLighting



、シャドウチェックを追加する必要があります。

 ComputeLighting（P、N、V、s）{
    i = 0.0
    scene.Lights {
        light.type == ambient {
            i + = light.intensity
        } else {
            light.type == point {
                L = light.position-P
                t_max = 1
            } else {
                L = light.direction
                t_max = inf
             }

            ＃シャドウチェック
            shadow_sphere、shadow_t = ClosestIntersection（P、L、0.001、t_max）
            shadow_sphere！= NULLの場合
                続ける

            ＃拡散
            n_dot_l =ドット（N、L）
            n_dot_l> 0の場合
                i + = light.intensity * n_dot_l /（長さ（N）*長さ（L））

            ＃ミラーリング
            if s！= -1 {
                R = 2 * N *ドット（N、L）-L
                r_dot_v =ドット（R、V）
                r_dot_v> 0の場合
                    i + = light.intensity * pow（r_dot_v /（長さ（R）*長さ（V））、s）
             }
         }
     }
    私を返す
 } 

新しくレンダリングされたシーンは次のようになります。





ソースコードと動作デモ>>



これで、すでに何かを取得しています。

リフレクション

光沢のあるオブジェクトが得られました。しかし、実際にミラーのように動作するオブジェクトを作成することは可能ですか？もちろん、実際には、レイトレーサーでの実装は非常に単純ですが、最初はわかりにくいかもしれません。



ミラーの仕組みを見てみましょう。鏡を見ると、鏡から反射する光線が見えます。光線は、表面の法線に対して対称に反射され







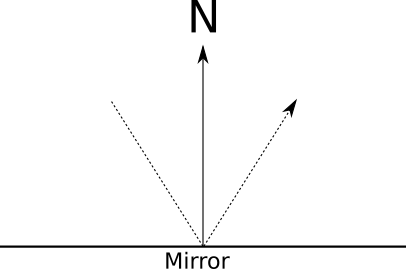
ます。光線をトレースし、ミラーが最も近い交差点であるとします。光線は何色ですか？明らかに、これはミラーの色ではなく、反射ビームを持つ任意の色です。必要なのは、反射光線の方向を計算し、この方向から落ちてくる光の色が何であるかを調べることです。与えられた光線に対してこの方向から落ちる光の色を返す関数があれば...



ああ、待って、私たちはそれを持っています：それは呼ばれTraceRay



ます。



そこで、メインループTraceRay



から始めて、カメラから放出される「光線」が「見る」ものを確認します。TraceRay



光線が反射オブジェクトを認識していると判断した場合、反射光線の方向を計算して...を呼び出すだけで済みます。



この時点で、最後の3つの段落を理解するまで読み直すことをお勧めします。再帰的なレイトレーシングについて初めて読む場合は、数回読み直して、実際に理解する前に少し考える必要があります。



時間をかけて、お待ちください。



...



ユーレカのこの素晴らしい瞬間からの幸福感！少し寝て、これを少し形式化しましょう。



すべての再帰アルゴリズムで最も重要なことは、無限ループを防ぐことです。このアルゴリズムには明らかな終了条件があります。光線が非反射オブジェクトに当たるか、何にも当たらない場合です。しかし、無限のサイクルに陥ることができる単純なケースがあります。無限の廊下の効果です。鏡を別の鏡の反対側に置いて、自分の中の無限のコピーを見ると現れます！



この問題を防ぐには多くの方法があります。アルゴリズムの再帰制限を導入します。彼は彼が行くことができる「深さ」を制御します。彼に電話しましょう$$$r$ 。 で $$r = 0、オブジェクトが表示されますが、反射はありません。$r = 0$で $$r = 1いくつかのオブジェクトといくつかのオブジェクトの反射が表示されます。$r = 1$で $$r = 2いくつかのオブジェクト、いくつかのオブジェクトの反射、およびいくつかのオブジェクトの反射の反射が表示されます。$r = 2$などなど。一般的な場合、この段階ではすでに違いがほとんど目立たないため、2〜3レベル以上に深く行くことはほとんど意味がありません。



別の区別を作成します。「反射率」には「かどうか」という意味がありません。オブジェクトは部分的に反射し、部分的に色付けすることができます。各面に番号を割り当てます$$$0$ 前に $$1、その反射率を決定します。その後、この数値に比例して、ローカルに点灯した色と反射した色を混合します。そして最後に、再帰呼び出しが受け取るパラメーターを決定する必要がありますか？光線はオブジェクトの表面、つまり点から始まります$1$



TraceRay



$$$P$ 。 ビームの方向は、反射する光の方向です $$$P$ ;でTraceRay



我々が持っています$$→ D、つまりカメラからの方向$\vec{D}$$$P、光の動きとは反対、つまり反射ビームの方向は$P$$$→ - Dの反射に対して、$\vec{-D}$$$$\vec{N}$ 。 影で起こることと同様に、オブジェクトに自分自身を反映させたくないので、 $$$t_{min} = \epsilon$ 。 オブジェクトの距離に関係なく、オブジェクトが反映されるのを確認したいので、 $$$t_{max} = +\infty$ 。 そして最後-再帰制限は、現在の再帰制限よりも1つ少ないです。

反射レンダリング

レイトレーサーコードに反射を追加しましょう。



前と同様に、まず、シーンを変更します。

 sphere {
    center =（0、-1、3）
    半径= 1
    color =（255、0、0）＃赤
    鏡面反射= 500＃ブリリアント
    反射= 0.2＃わずかに反射
 }
sphere {
    中央=（-2、1、3）
    半径= 1
    color =（0、0、255）＃青
    鏡面反射= 500＃ブリリアント
    反射= 0.3＃もう少し反射
 }
sphere {
    中央=（2、1、3）
    半径= 1
    color =（0、255、0）＃緑
    鏡面反射= 10＃少し華麗
    反射= 0.4＃さらに反射
 }
sphere {
    color =（255、255、0）＃黄色
    中央=（0、-5001,0）
    半径= 5000
    鏡面反射= 1000＃非常に素晴らしい
    反射= 0.5＃半反射
 } 

いくつかの場所で「反射ビーム」式を使用しているので、それを取り除くことができます。彼女はビームを取得します$$→ Rおよび通常$\vec{R}$$$→ N、戻る$\vec{N}$$$→ R、比較的反射$\vec{R}$$$$\vec{N}$ ：

 ReflectRay（R、N）{
    return 2 * N * dot（N、R）-R;
 } 

唯一の変更ComputeLighting



は、反射方程式をこの新しい方程式に置き換えることReflectRay



です。



mainメソッドにわずかな変更が加えられました- TraceRay



再帰制限を上位レベルに渡す必要があります。

 color = TraceRay（O、D、1、inf、recursion_depth） 

定数recursion_depth



は、3または5などの妥当な値に設定できます。



重要な変更TraceRay



は、反射を再帰的に計算する最後の近くでのみ発生します。

 TraceRay（O、D、t_min、t_max、深度）{
    closest_sphere, closest_t = ClosestIntersection(O, D, t_min, t_max)

    if closest_sphere == NULL
        return BACKGROUND_COLOR

    #   
    P = O + closest_t*D #   
    N = P - closest_sphere.center #       
    N = N / length(N)
    local_color = closest_sphere.color*ComputeLighting(P, N, -D, sphere.specular)

    #         ,   
    r = closest_sphere.reflective
    if depth <= 0 or r <= 0:
        return local_color

    #   
    R = ReflectRay(-D, N)
    reflected_color = TraceRay(P, R, 0.001, inf, depth - 1)

    return local_color*(1 - r) + reflected_color*r
 } 

結果がわかる：







ソースコードと作業デモ>>



再帰の深さの制限をよりよく理解するために、次のようにレンダリングを詳しく見てみましょう。$$$r = 1$ ：







そして、これは同じシーンの同じ拡大図で、今回は $$$r = 3$ ：







ご覧のとおり、違いは、オブジェクトの反射の反射の反射を見るのか、オブジェクトの反射だけを見るのかです。

任意のカメラ

レイトレーシングの説明の最初に、2つの重要な仮定を立てました。カメラは $$（0 、0 、0 ）と方向付け$(0, 0, 0)$$$→ Z +、上方向は$\vec{Z_+}$$$$\vec{Y_+}$ 。このセクションでは、これらの制限を取り除き、シーン内の任意の場所にカメラを配置し、任意の方向に向けることができるようにします。



状況から始めましょう。おそらく気づいたでしょう$$Oは、擬似コード全体で1回だけ使用されます。トップレベルメソッドでカメラから発せられる光線の開始点として。カメラの位置を変更したい場合。する唯一のことは、異なる値を使用することです$O$$$$O$ 。



位置を変更すると、光線の方向に影響しますか？決して。光線の方向は、カメラから投影面に通過するベクトルです。カメラを移動すると、投影面はカメラとともに移動します。つまり、それらの相対位置は変化しません。



次に、方向に注目しましょう。回転する回転行列があるとしましょう$$（0 、0 、1 ）ビューの所望の方向に、および$(0, 0, 1)$$$（0 、1 、0 ） -右方向に「アップ」（及びとして、次に定義することによって、それを行うために必要とされるべきである回転行列であります$(0, 1, 0)$$$$(1, 0, 0)$ ） カメラを単純に回転させても、カメラの位置は変わりません。しかし、方向は変化しており、カメラ全体と同じ回転だけを受けます。つまり、方向性があれば$$→ Dと回転行列$\vec{D}$$$Rを回転させた$R$$$Dはただ$D$$$$\vec{D}R$ 。



トップレベルの機能のみが変更されます：

 [-Cw / 2、Cw / 2]のxの場合{
    [-Ch / 2、Ch / 2]のyの場合{
        D = camera.rotation * CanvasToViewport（x、y）
        color = TraceRay（camera.position、D、1、inf）
        canvas.PutPixel（x、y、色）
     }
 } 

別の位置から別の向きで観察すると、シーンは次のようになります。







ソースコードと作業デモ>>

次に行く場所

まだ調査していないいくつかの興味深いトピックの簡単な概要で、作業の最初の部分を終了します。

最適化

はじめに述べたように、さまざまな可能性を説明し、実装する最も理解しやすい方法を検討しました。したがって、レイトレーサーは完全に機能しますが、特に高速ではありません。以下に、トレーサーを高速化するために独自に調査できるアイデアをいくつか示します。ちょっとした楽しみのために、実装の前後にランタイムを測定してみてください。あなたは非常に驚くでしょう！

並列化

レイトレーサーを高速化する最も明白な方法は、複数のレイを同時にトレースすることです。カメラからの各ビームは他のすべてのビームから独立しており、ほとんどの構造は読み取り専用であるため、同期の問題による困難や困難を伴うことなく、中央処理装置のコアごとに1つのビームをトレースできます。



実際、レイトレーサーは、その性質上、非常に簡単に並列化できるため、非常に並列化可能と呼ばれるアルゴリズムのクラスに属します。

値のキャッシュ

IntersectRaySphere



レイトレーサーが通常ほとんどの時間を費やす計算値を検討してください。

 k1 =ドット（D、D）
    k2 = 2 *ドット（OC、D）
    k3 =ドット（OC、OC）-r * r 

これらの値の一部は、シーン全体で一定です-球体がどのように配置されているかを知るとすぐに、r*r



それらdot(OC, OC)



はもはや変化しません。シーンのロード中にそれらを一度計算し、レルム自体に保存できます。球体が次のフレームで移動する必要がある場合は、それらを再カウントする必要があります。dot(D, D)



与えられた光線の定数ですので、それを計算しClosestIntersection



て渡すことができますIntersectRaySphere



。

シャドウの最適化

途中で別のオブジェクトを見つけたのでオブジェクトは、光源に影の相対的に位置されている場合は、原因同じオブジェクトへの彼女のポイントとの隣人は、あまりにも、（これが呼び出された光源に対する影になっていることを高い確率があり、影の一貫性：）







つまりは、ポイントと光源の間のオブジェクトを探すとき、最初に、同じ光源に関連して前のポイントにシャドウを適用した最後のオブジェクトが現在のポイントをシャドウしないかどうかを確認できます。もしそうなら、我々は終了することができます。そうでない場合は、通常の方法で他のオブジェクトのチェックを続けます。



同様に、光線とシーン内のオブジェクトとの交差を計算する場合、実際には最も近い交差は必要ありません。少なくとも1つの交差があることを知っているだけです。ClosestIntersection



最初の交差点が見つかるとすぐに結果を返す特別なバージョンを使用できます（このためにclosest_t



、ではなくブール値を計算して返す必要があります）。

空間構造

光線と各球の交差を計算することは、リソースのかなりの無駄です。個々の交差を計算する必要なく、オブジェクトのグループ全体を一気にドロップできる多くのデータ構造があります。



このような構造の詳細な検討は、この記事のトピックには関係ありませんが、一般的な考え方は次のとおりです。互いに近い複数の領域があるとします。これらすべての球を含む最小の球の中心と半径を計算できます。光線がこの境界球と交差しない場合は、光線が含まれる球と交差しないことを確認でき、交差の1回のチェックでこれを行うことができます。もちろん、球体と交差する場合、その球体に含まれる球体と交差するかどうかを確認する必要があります。



これについては、バウンディングボリュームの階層について読むことで学習できます。

ダウンサンプリング

以下にレイトレーサーを作成する簡単な方法を示します。 $$N倍高速：で計算$N$$$N倍少ないピクセル！ピクセルの光線をトレースするとします$N$



$$$(10, 100)$ そして $$（12 、100 ）、及びそれらが同じオブジェクトに落ちます。論理的には、ピクセルの光線は$(12, 100)$$$（11 、100 ）も、同じ目的に入るすべてのステージ上から交差点の初期サーチをスキップして、その時点での色の計算に直接行きます。水平方向と垂直方向にこれを行うと、ビームシーンの交差の主要な計算よりも最大75％少ない実行が可能です。もちろん、この方法で非常に薄いオブジェクトを簡単にスキップできます。以前に検討したものとは異なり、これは「間違った」最適化です。その使用結果は、それなしで得たものと同一ではないためです。ある意味、この節約をごまかしています。トリックは、正しく保存することを推測し、満足のいく結果を提供することです。$(11, 100)$

その他のプリミティブ

前のセクションでは、球体を数学的な観点から簡単に操作できるため、球体をプリミティブとして使用しました。しかし、これを達成したら、他のプリミティブを簡単に追加できます。



ビューの観点からTraceRay



、任意のオブジェクトが適切である可能性があることに注意してください。そのためには、2つの値のみを計算する必要があります。$$ビームとオブジェクト間の最も近い交点、および交点での法線の t。レイトレーサーの他のすべては、オブジェクトのタイプに依存しません。三角形は良い選択です。まず、光線と三角形を含む平面との交差を計算する必要があります。交差がある場合は、ポイントが三角形の内側にあるかどうかを判断します。$t$

構造ブロック形状

実装が比較的簡単な非常に興味深いタイプのオブジェクトがあります。他のオブジェクト間のブール演算です。たとえば、2つの球体の交点はレンズに似たものを作成でき、大きな球体から小さな球体を差し引くと、デススターに似たものを得ることができます。



どのように機能しますか？オブジェクトごとに、光線がオブジェクトに出入りする場所を計算できます。たとえば、球の場合、光線は$$m i n （t 1、t 2）および$min(t_1, t_2)$$$$max(t_1, t_2)$ 。2つの球の交差を計算する必要があるとします。光線は、両方の球の内側にある場合は交差の内側にあり、反対の場合には外側にあります。減算の場合、光線は最初のオブジェクトの内側にあるときに内側にありますが、2番目のオブジェクトの内側にはありません。



より一般的には、光線と$$$A \bigodot B$ （どこ $$⨀はブール演算子です）、最初に光線の交差を個別に計算する必要があります$\bigodot$$$Aとビーム$A$$$B、各オブジェクトの「内部」間隔を提供します$B$$$$R_A$ そして $$$R_B$ 。 次に計算する $$R A ⨀ R Bの「内側」の範囲内に位置し、$R_A \bigodot R_B$$$$A \bigodot B$ 。 最初の値を見つけるだけです $$tは、「内部」間隔と間隔の両方にあります$t$$$[ t m i n、t m a x ]：交差点での法線は、交差点を作成するオブジェクトの法線、または元のオブジェクトの「外側から」または「内側から」のどちらに見えるかに応じて、その反対です。もちろん$[t_{min}, t_{max}]$











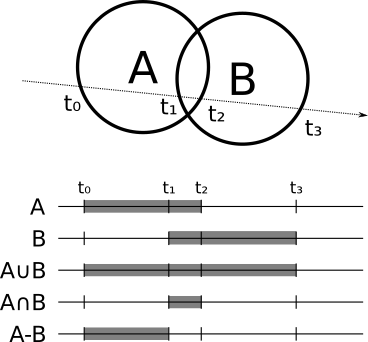
$$$A$ そして $$Bはプリミティブである必要はありません。それら自体がブール演算の結果になる可能性があります！これを純粋に実装する場合、それらから交差点と法線を取得できる限り、それらが何であるかを知る必要さえありません。したがって、3つの球体を使用して、たとえば次のように計算できます。$B$$$$(A \cup B) \cap C$ 。

透明性

すべてのオブジェクトが不透明である必要はなく、一部は透明である場合があります。



透明度の実装は、反射の実装に非常に似ています。ビームが部分的に透明な表面に当たると、以前と同様に、ローカル色と反射色を計算しますが、追加の色- 別の呼び出しで受信したオブジェクトを通過する光の色も計算しますTraceRay



。次に、オブジェクトの透明度を考慮して、この色とローカル色および反射色を混ぜる必要があります。それだけです。

屈折

実際には、光線が透明なオブジェクトを通過すると、方向が変わります（したがって、ストローがコップ一杯の水に浸されると、「壊れた」ように見えます）。方向の変化は、次の式に従って各材料の屈折率に依存します。

$$

$${sin(\alpha_1) \over sin(\alpha_2)} = { n_2 \over n_1 }$$

どこで $$$\alpha_1$ そして $$α 2 -交差点の前後の面の光線と法線との間の角度であり、そして$\alpha_2$$$$n_1$ そして $$n 2は、物体の外側と内側の材料の屈折率です。$n_2$



例えば $$n はx で約z d で、ほぼ等しい$n_{}$$$$1.0$ 、そして $$N におけるD Sにほぼ等しいです。$n_{}$$$$1.33$ 。 つまり、ある角度で水に入るビームの場合 $$60 ∘ GET$60^\circ$

$$

$${sin(60) \over sin(\alpha_2)} = {1.33 \over 1.0}$$

$$

$$sin(\alpha2) = {sin(60) \over 1.33}$$

$$

$$\alpha2 = arcsin({sin(60) \over 1.33}) = 40.628^\circ$$

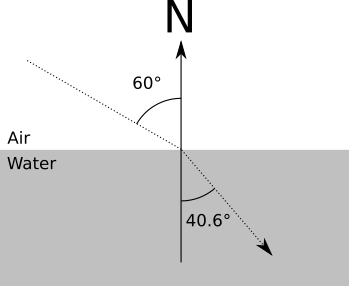
少しの間停止してください：建設的なブロックジオメトリと透明度を実装すると、物理的に正しい虫眼鏡のように動作する虫眼鏡（2つの球の交点）をシミュレートできます！

スーパーサンプリング

スーパーサンプリングは、速度ではなく精度を追求するときのサブサンプリングの大まかな反対です。 2つの隣接するピクセルに対応する光線が2つの異なるオブジェクトに当たるとします。各ピクセルを対応する色で着色する必要があります。



ただし、最初に行ったアナロジーを忘れないでください。各光線は、「グリッド」の各正方形の「定義」色を指定する必要があります。書き込みごとに1つの光線を使用して、正方形の中央を通過する光線の色が正方形全体を決定することを条件付きで決定しますが、そうでない場合があります。



この問題を解決するには、ピクセルごとに複数の光線（4、9、16など）をトレースし、それらを平均してピクセルの色を取得します。



もちろん、この場合、レイトレーサーは4倍、9倍、または16倍遅くなります。これは、ダウンサンプリングがそれを行うのと同じ理由です。 $$N倍高速。幸いなことに、妥協点があります。表面に沿ったオブジェクトのプロパティは滑らかに変化します。つまり、ピクセルごとに4つの光線が放出され、わずかに異なるポイントで1つのオブジェクトに当たると、シーンの外観は大きく改善されません。したがって、ピクセルごとに1つのレイから開始し、隣接するレイを比較できます。他のオブジェクトに当たるか、変換されたしきい値よりも色が異なる場合は、両方にピクセル分割を適用します。$N$

レイトレーサーの擬似コード

以下は、レイトレーシングの章で作成した擬似コードの完全版です。

 CanvasToViewport（x、y）{
    return（x * Vw / Cw、y * Vh / Ch、d）
 }


ReflectRay（R、N）{
    return 2 * N * dot（N、R）-R;
 }


ComputeLighting（P、N、V、s）{
    i = 0.0
    scene.Lights {
        light.type == ambient {
            i + = light.intensity
        } else {
            light.type == point {
                L = light.position-P
                t_max = 1
            } else {
                L = light.direction
                t_max = inf
             }

            ＃影を確認する
            shadow_sphere、shadow_t = ClosestIntersection（P、L、0.001、t_max）
            shadow_sphere！= NULLの場合
                続ける

            ＃拡散
            n_dot_l =ドット（N、L）
            n_dot_l> 0の場合
                i + = light.intensity * n_dot_l /（長さ（N）*長さ（L））

            ＃シャイン
            if s！= -1 {
                R = ReflectRay（L、N）
                r_dot_v =ドット（R、V）
                r_dot_v> 0の場合
                    i + = light.intensity * pow（r_dot_v /（長さ（R）*長さ（V））、s）
             }
         }
     }
    私を返す
 }


ClosestIntersection（O、D、t_min、t_max）{
    最も近いt = inf
    nearest_sphere = NULL
    scene.Spheres {の球の場合
        t1、t2 = IntersectRaySphere（O、D、球体）
        [t_min、t_max]のt1およびt1 <closest_tの場合
            最も近いt = t1
            最も近い球体=球体
        [t_min、t_max]のt2およびt2 <closest_tの場合
            最も近いt = t2
            最も近い球体=球体
     }
    最も近い_sphere、最も近い_tを返す
 }


TraceRay（O、D、t_min、t_max、深度）{
    nearest_sphere、closest_t = ClosestIntersection（O、D、t_min、t_max）

    nearest_sphere == NULLの場合
        BACKGROUND_COLORを返します

    ＃ローカルカラーの計算
    P = O +最も近い_t * D＃交点の計算
    N = P-nearest_sphere.center＃交差点での球の法線を計算します
    N = N /長さ（N）
    local_color = nearest_sphere.color * ComputeLighting（P、N、-D、sphere.specular）

    ＃再帰制限に到達した場合、またはオブジェクトが反射していない場合、完了です
    r = nearest_sphere.reflective
    深さ<= 0またはr <= 0の場合：
        local_colorを返します

    ＃反射色の計算
    R = ReflectRay（-D、N）
    reflected_color = TraceRay（P、R、0.001、inf、depth-1）

    local_color *（1-r）+反射色* rを返します
 }


[-Cw / 2、Cw / 2]のxの場合{
    [-Ch / 2、Ch / 2]のyの場合{
        D = camera.rotation * CanvasToViewport（x、y）
        color = TraceRay（camera.position、D、1、inf）
        canvas.PutPixel（x、y、色）
     }
 } 

そして、例をレンダリングするために使用されるシーンは次のとおりです。

 viewport_size = 1 x 1
projection_plane_d = 1

sphere {
    center =（0、-1、3）
    半径= 1
    color =（255、0、0）＃赤
    鏡面反射= 500＃ブリリアント
    反射= 0.2＃わずかに反射
 }
sphere {
    中央=（-2、1、3）
    半径= 1
    color =（0、0、255）＃青
    鏡面反射= 500＃ブリリアント
    反射= 0.3＃もう少し反射
 }
sphere {
    中央=（2、1、3）
    半径= 1
    color =（0、255、0）＃緑
    鏡面反射= 10＃少し華麗
    反射= 0.4＃さらに反射
 }
sphere {
    color =（255、255、0）＃黄色
    中央=（0、-5001,0）
    半径= 5000
    鏡面反射= 1000＃非常に素晴らしい
    反射= 0.5＃半反射
 }


ライト{
    タイプ=アンビエント
    強度= 0.2
 }
ライト{
    タイプ=ポイント
    強度= 0.6
    位置=（2、1、0）
 }
ライト{
    タイプ=方向
    強度= 0.2
    方向=（1、4、4）
 }