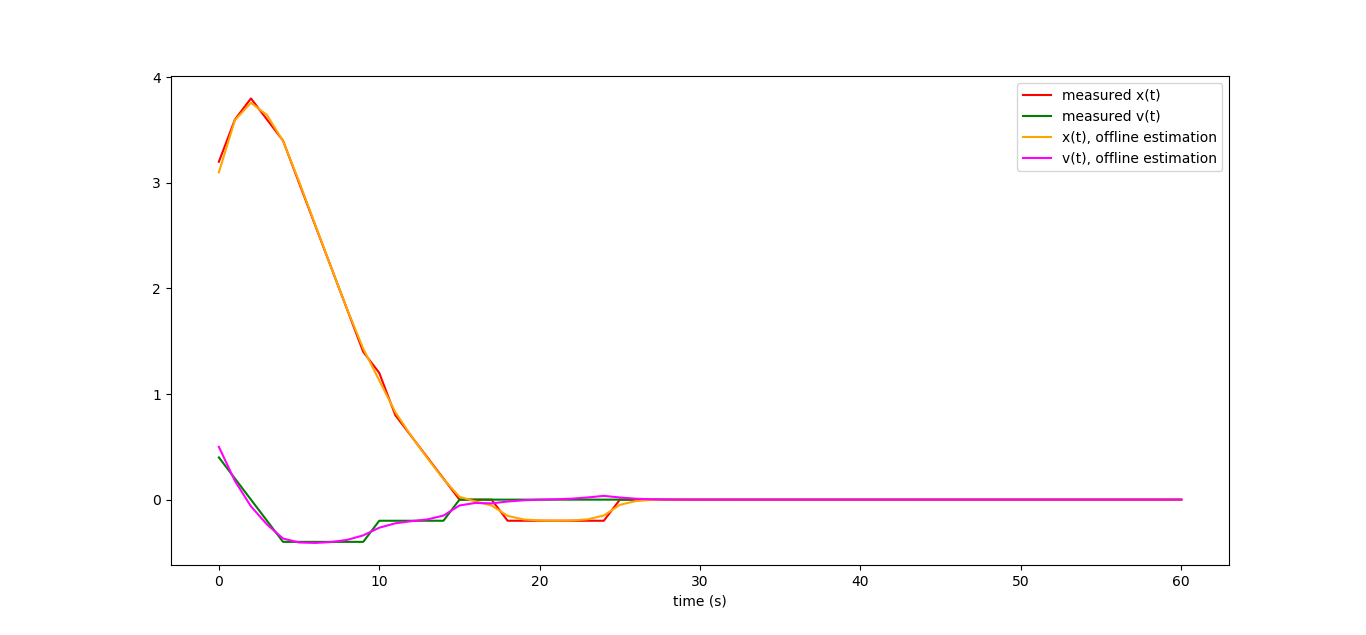
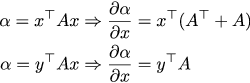- 最小二乗法
- 線形2次コントローラー、入門
- 線形2次レギュレータと線形オブザーバー
私は制御理論の専門家ではありません。ただ教科書を読んでいます。 私の仕事は理論を理解し、実践することです。 この記事は単なる理論です(まあ、少し付属のコードです)。次に、練習について説明します。その一部を以下に示します。
修正および追加は大歓迎です。 何百回も、私はまず自分のためにこれらのテキストを書くことを思い出します。 このサイトは私にとっては一種の公開ノートブックであり、ちなみに私は定期的にアクセスしています。 念のために、私は自分の人生をうまく表現したあごひげを生やしたジョークを思い出します。
2人の教師間の会話:
-さて、今年私は愚かなグループを得ました!
-それで?
-定理の説明を想像してください-彼らは理解していません! もう一度説明します-彼らは理解しません! 3回目の説明で、私はすでに理解しました。 しかし、彼らは理解していません...
線形2次レギュレータ、側面図
LQR:問題の声明
それで、 前の記事で話したこと 、つまりロシアの学校が最適な規制当局の分析的構築と呼んでいることを思い出しましょう。 その記事の例を取り上げます。
ある時点kでの状態が座標x_kと速度v_kによって特徴付けられる自動車があるとします。 実験は特定の初期状態(x_0、v_0)から始まり、タスクは座標0で車を止めることです。 ガス/ブレーキ、つまり加速u_kを介して操作できます。 この情報は、人から人へ送信するのに便利な形式で記述します。 口頭での説明は面倒であり、いくつかのタクトを可能にします。
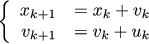
マトリックスはさまざまな表現に置き換えることができるため、この情報をマトリックス形式で記述する方が便利です。これにより、言語は非常に柔軟になり、さまざまな問題を記述することができます。
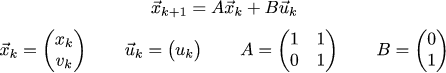
そのため、システムのダイナミクスについては説明しましたが、目標または正確なガバナンスと見なされるものについては説明しませんでした。 車の軌道と制御信号のシーケンスをパラメーターとして使用する次の2次関数を作成してみましょう。
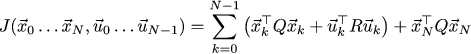
この関数の値を最小化する車の軌跡を見つけようとします。 この関数は、目標間の妥協点を設定します。合理的な量の制御を維持しながら、システムをできるだけ早くゼロに収束させます(速度を落とす必要はありません!)
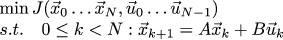
合計すると、入力変数に線形制約がある関数を最小化するタスクがあります。 自動車に関する特定のタスクについては、前回の目的でこのようなウェイト1と256を選択しました。
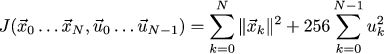
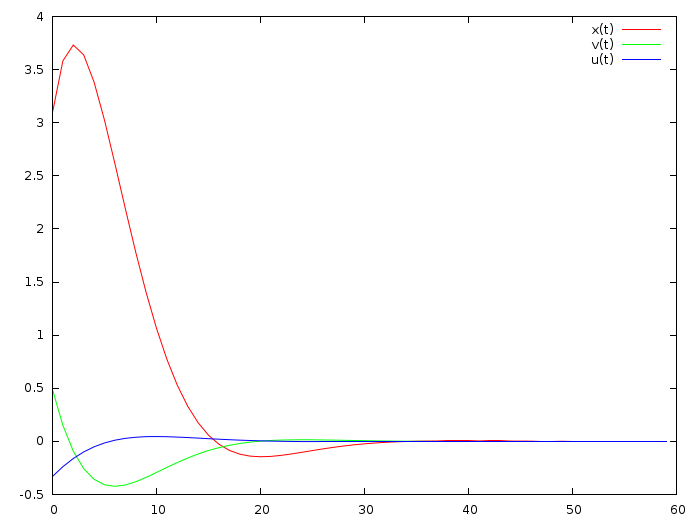
最初の時点で車がポジション3.1にあり、速度が毎秒0.5メートルの場合、最適な制御は次のようになります(前回の記事から引用)。
LQR:問題を解決します
前回とは少し異なる方法で同じ曲線を描いてみましょう。 録音量は非常に面倒なので、マトリックス形式に減らしましょう。 まず、軌道全体と制御シーケンス全体を健全な行列列に縮小します。
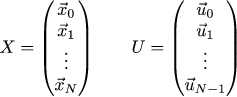
次に、座標と制御の関係を次のように記述できます。
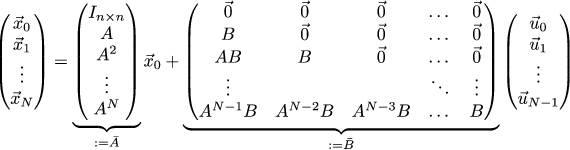
またはさらに簡単に:
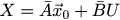
この記事では、マトリックス上のスティックは、単一の反復を記述する小さなマトリックスをタスク全体で大きな反復に削減することを意味します。 特定の問題では、行列A ^ nの次数は次のとおりです。
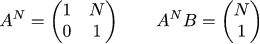
明確にするために、explicitlyとB̄を明示的に記述しましょう。

そして、私もこれらの行列を埋めるソースコードをnumpyで提供します:
import matplotlib.pyplot as plt import numpy as np np.set_printoptions(precision=3,suppress=True,linewidth=128,threshold=100000) def build_Abar(A, N): n = A.shape[0] Abar = np.matrix( np.zeros(((N+1)*n,n)) ) for i in range(N+1): Abar[i*n:(i+1)*n,:] = A**i return Abar def build_Bbar(A, B, N): (n,m) = B.shape Bbar = np.matrix( np.zeros(((N+1)*n,N*m)) ) for i in range(N): for j in range(Ni): Bbar[(Ni)*n:(N-i+1)*n,(Nij-1)*m:(Nij)*m] = (A**j)*B return Bbar A = np.matrix([[1,1],[0,1]]) B = np.matrix([[0],[1]]) (n,m) = B.shape N=60 Abar = build_Abar(A, N) Bbar = build_Bbar(A, B, N)
二次形式の大きな行列と係数に還元します。

私たちの特定の車の問題では、Q̄は単位行列であり、R̄はスカラー256を掛けた単位行列です。その後、品質管理関数は非常に簡単に行列形式で記述されます。
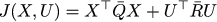
そして、1つの線形制約を持つこの関数の最小値を探しています:
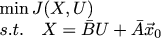
私自身に注意してください:ラグランジュ乗数、ルジャンドルtransformation関数、およびこれから得られたハミルトン関数を扱う絶好の機会です。 また、LQRの説明がこれからどのように動的計画法とリカッチ方程式を通して続くか。 どうやら、あなたはまだ記事を書く必要があります:)
私は怠け者なので、今回は最も直接的な方法で行きます。 Jは、互いに線形関係にある2つの引数に依存します。 線形制約で関数を最小化する代わりに、余分な変数を削除します。つまり、Xの出現をx_0 +B̄Uに置き換えます。
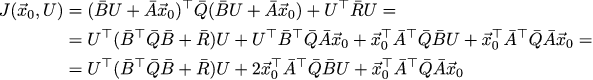
これはかなり退屈ですが、脳を必要としない完全に機械的な結論です。 最後から2番目の行に移動するとき、Q̄が対称であるという事実を利用して、Q̄+Q̄^ T = 2Q̄と書くことができました。
ここで、二次関数の最小値を見つけるだけで、変数に制限は課されません。 私たちは学校の10年生を思い出し、ゼロの偏微分に相当します。
通常の多項式を微分できる場合は、行列の微分も同様に使用できます。 念のため、差別化のルールを思い出します。
繰り返しますが、ちょっとした退屈な波線の記述があり、制御ベクトルUに関して偏微分が得られます(Q̄とR̄の対称性を使用しました)。
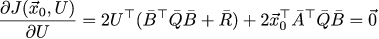
次に、最適な制御ベクトルU *は次のように見つけることができます。
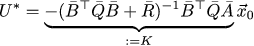
さて、どのように波線を書きますが、まだ何も描画していませんか? それを修正しましょう!
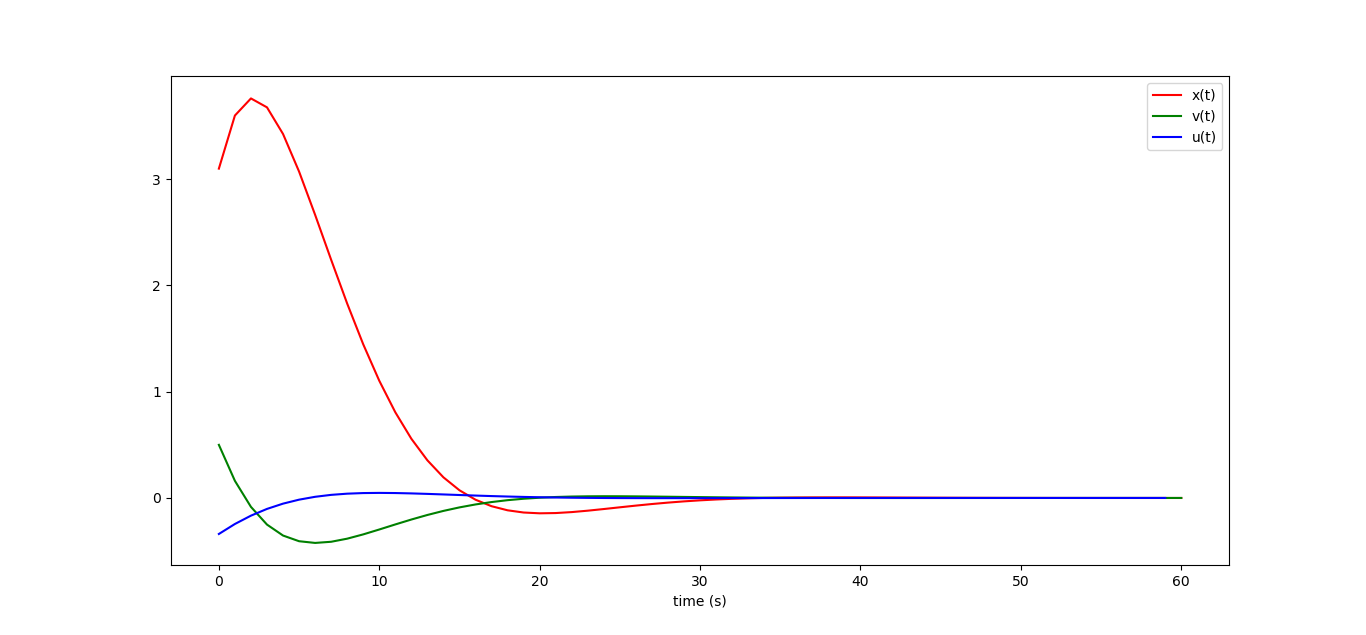
K=-(Bbar.transpose()*Bbar+np.identity(N*m)*256).I*Bbar.transpose()*Abar print("K = ",K) X0=np.matrix([[3.1],[0.5]]) U=K*X0 X=Abar*X0 + Bbar*U plt.plot(range(N+1), X[0::2], label="x(t)", color='red') plt.plot(range(N+1), X[1::2], label="v(t)", color='green') plt.plot(range(N), U, label="u(t)", color='blue') plt.legend() plt.show()
これにより、次の図が表示されます。これは、前の記事で受け取ったものと完全に一致することに注意してください( ここに描画します )。
LQR:ソリューション分析
制御とシステムステータスの線形接続
そのため、理論は(イベントの長い地平線で)最適な制御は最終目標までの残りの距離に線形に依存することを教えてくれます。 前回、1次元の場合、2次元の単語を信じることでそれを証明しました。 今回も厳密に証明するつもりはありませんが、ラグランジュ乗数については後で説明します。 しかし、それは直感的に明らかです。 結局、式U = K * x0が得られました。ここで、行列Kはシステムの状態に依存せず、微分方程式の構造(行列AおよびB)にのみ依存します。
つまり、u_0 = k_0 * x_0です。 ところで、k_0は[-0.052 -0.354]に等しくなりました。
K = [[-0.052 -0.354]
[-0.034 -0.281]
[-0.019 -0.215]
[-0.008 -0.158]
[ 0. -0.11 ]
...
この結果を、OLSの助けを借りて得た結果と、Riccati方程式を解いて得られた結果(前の記事へのコメント)を比較してください。 直観的に、u0がx_0に線形に依存する場合、長いイベントホライズンでは、x1でも同じである必要があります。
議論を続けると、コントロールu_iはu_i = k_0 * x_iと見なされるべきだと考えられます。 つまり、最適な制御は、定数ベクトルk_0とターゲットx_iまでの残差のスカラー積によって得られる必要があります。
しかし、私たちの結果は正反対です! u_i = k_i * x_0! つまり、システムの方程式の構造のみに依存し、その状態には依存しないシーケンスk_iが見つかりました。 そして、制御は定数ベクトル(システムの初期位置)と見つかったシーケンスのスカラー積を使用して取得されます...
つまり、すべてが順調であれば、等式k_0 * x_i = u_i = k_i * x_0が必要です。 k_0に等しいx_0を簡単にするために、説明的なグラフを描きましょう。 グラフの一方の軸では、マシンの座標を延期し、もう一方の軸では速度を延期します。 1つの点k_0 = x_0から開始して、ゼロ座標に収束する2つの異なる点k_iおよびx_iのシーケンスを取得します。
図面はこちらから入手できます 。
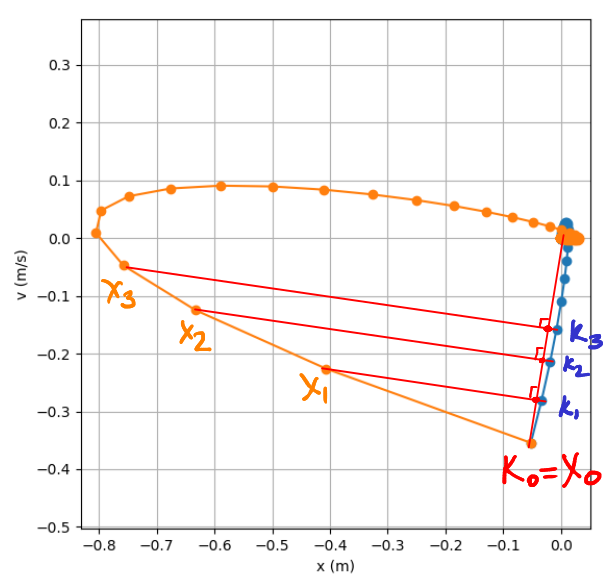
大まかであれば、k_i * x_0はベクトルx_0への投影k_iのシーケンスを形成します。 k_0 * x_iについても同様です。これは、k_0への射影x_iのシーケンスです。 これらの予測が一致していることは、グラフではっきりとわかります。 繰り返しますが、これは証拠ではなく、単なる説明です。
したがって、x_ {k + 1} =(A + BK)x_kという形式の動的システムを取得しました。 行列A + BKの固有値の絶対値が1未満の場合、このシステムは任意の初期x_0で原点に収束します。 つまり、この微分方程式の解は(行列)指数です。
負荷に耐えられなかった数学の学生がセッションに連れてこられた非常識な亡命で、彼らの一人はナイフと叫び声で走ります:「私はみんなを区別します!」 別の数学の学生を除いて、患者はばらばらになります。 最初のものが「私は区別します!」という叫びで部屋に突入したとき、2つめは「私はX度にいます!」 ナイフを振る最初の:「ゲームで差別化する!」
例として、私は誤って数百の異なるx_0を選択し、マシンの軌跡を描きました。 ここで絵を撮ります 。 結果の画像は次のとおりです。
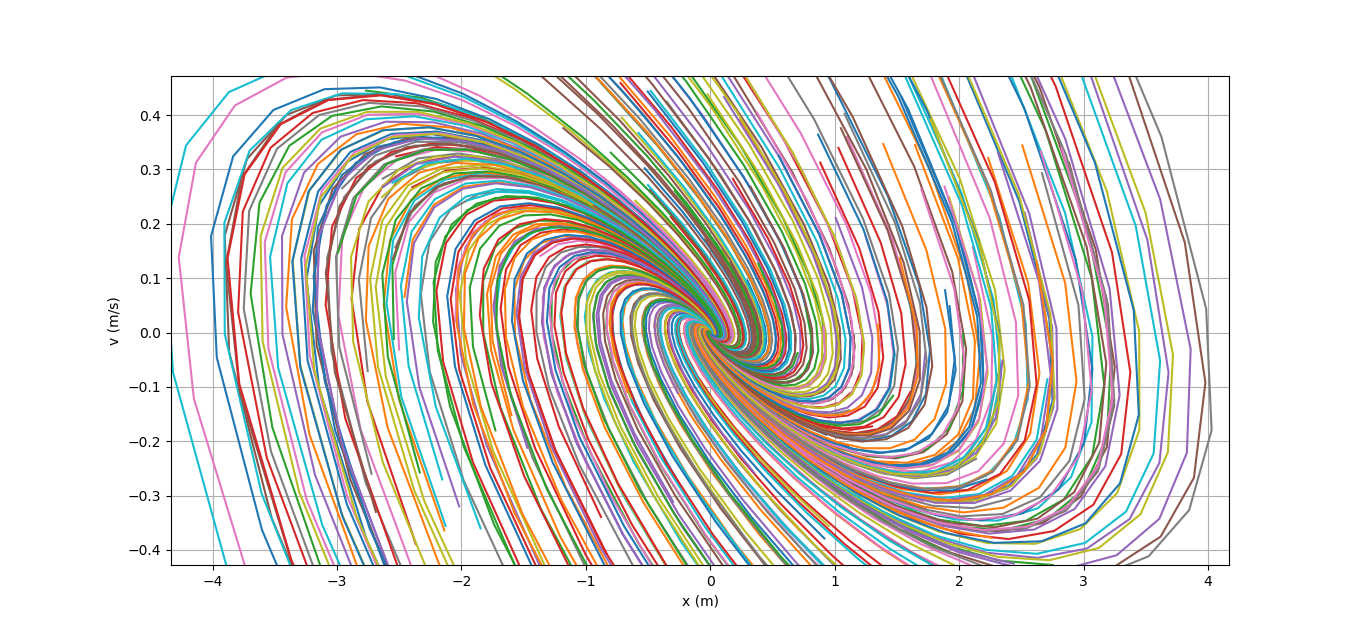
すべての軌跡はゼロに安全に収束します。軌跡のわずかなねじれは、行列A + BKが回転および収縮行列であることを示しています(絶対値が1よりも小さい複素固有値を持っています)。 私が間違っていなければ、この写真はフェーズポートレートと呼ばれます。
開閉制御ループ
したがって、関数Jを元気に最小化し、最適な制御ベクトルU0をK * X0として取得しました。
U=K*X0 X=Abar*X0 + Bbar*U
制御をu_i = k_0 * x_iとして考慮するか、それとも考慮するかにはまだ違いがありますか? システムに未説明の要因がある場合(つまり、ほとんどの場合)、巨大な問題が発生します。 私たちの車は水平面では転がりませんが、そのような丘はその途中で出会えると想像してみましょう:
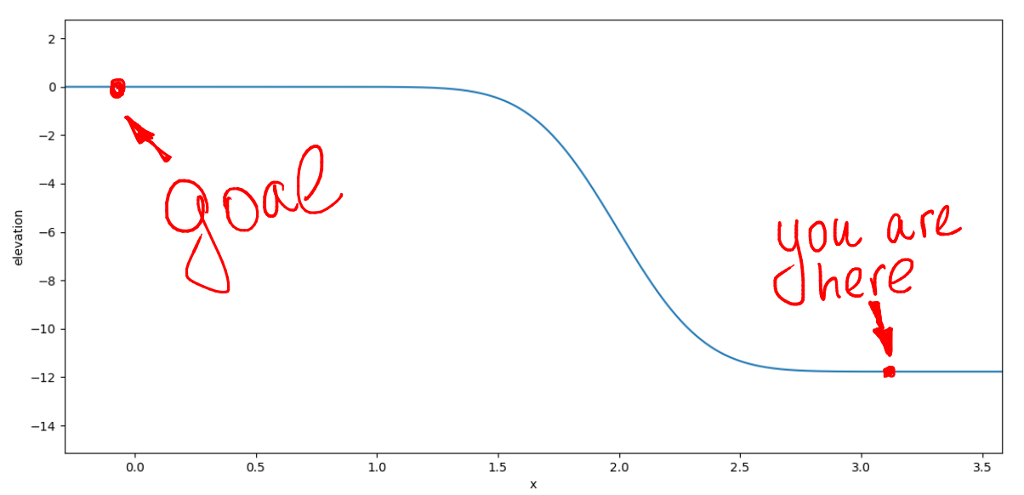
このスライドを考慮せずに最適な制御を計算すると、トラブルが発生する可能性があります
( ここに描画):
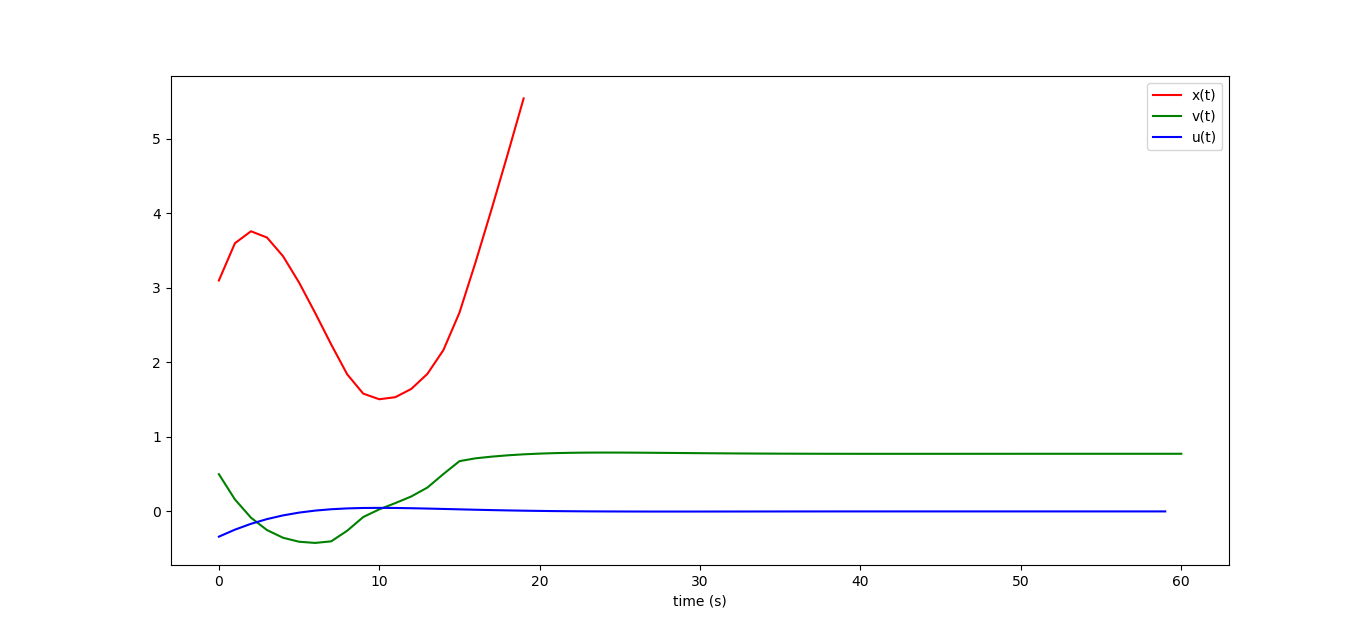
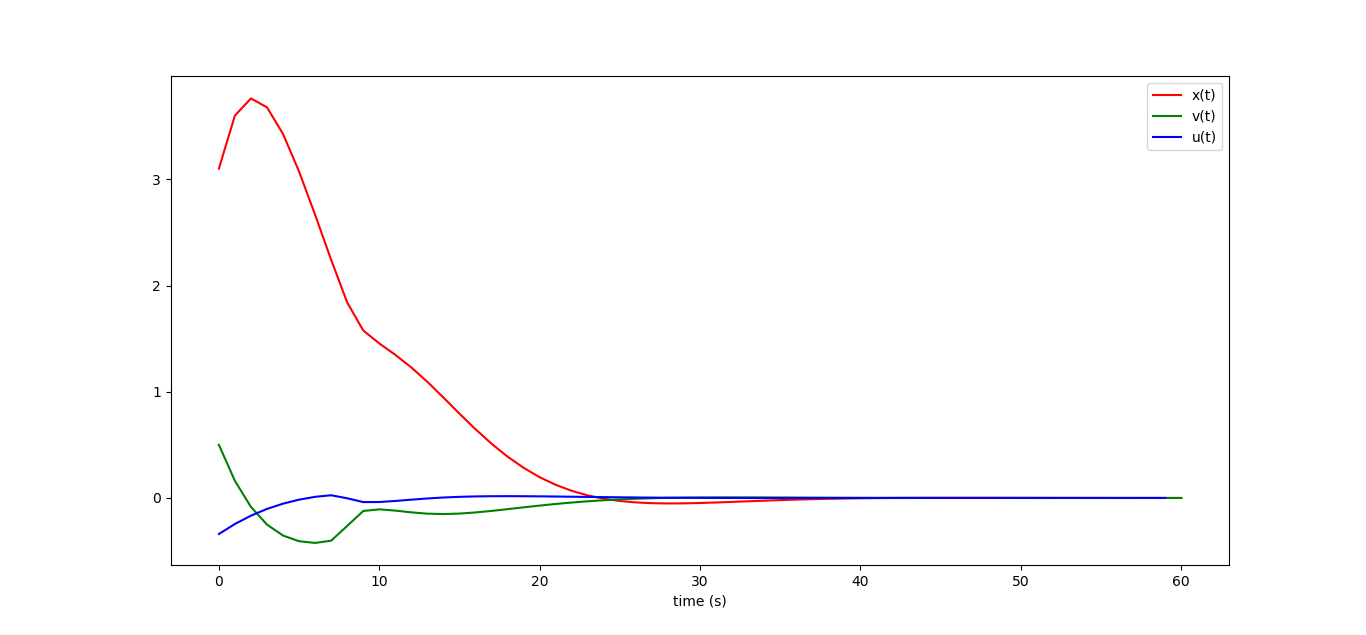
マシンは停止しないだけでなく、完全に右に無限に進みます。x_iグラフィックを3分の1だけ描画しても、直線的に成長します。 制御ループを閉じると、システムのダイナミクスの小さな乱れは壊滅的な結果につながりません。
for i in range(N): Xi = X[i*n:(i+1)*n,0] U[i*m:(i+1)*m,0] = K[0:m,:]*Xi idxslope = int((Xi[0,0]+5)/10.*1000.) if (idxslope<0 or idxslope>=1000): idxslope = 0 X[(i+1)*n:(i+2)*n,0] = A*Xi + B*U[i*m:(i+1)*m,0] + B*slope[idxslope]
線形オブザーバーの構築
したがって、動的システムを制御して、原点に到達するように努めることができます。 しかし、x = 0ではなくx = 3で車を停止させたい場合はどうでしょうか。 明らかに、現在の状態x_iから目的の結果を差し引くだけで十分で、その後はすべて通常どおりです。 さらに、この望ましい結果は永続的ではなく、時間とともに変化する可能性があります。 別の動的システムに従うことはできますか?
マシンを直接制御しないが、同時にそれを監視したいと仮定しましょう。 かなり低い解像度のセンサーを使用して、マシンの両方の状態を測定します。
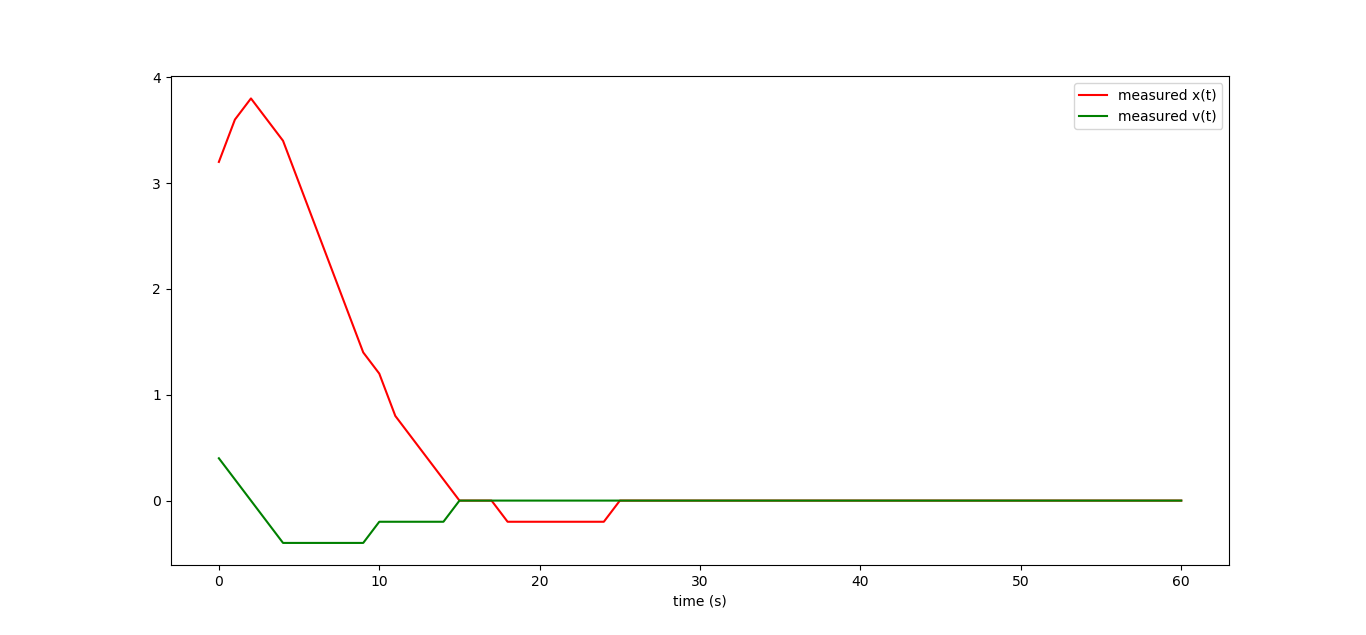
カーブを取り、その値を台無しにしました。 測定によって導入されたノイズを除去してみましょう。 いつものように、最小二乗で腕。
ハンマーを手に持っていると、周りのすべてが釘のように見えます。
したがって、私たちのマシンは法則x_ {k + 1} = A x_k + B u_kに従うので、同じ法則に従うディフューザー・オブザーバーを構築しましょう。
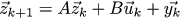
ここで、y_kは、実際の状態からどれだけ離れているかをオブザーバーに通知する修正項です。 前回同様、行列形式で方程式を書きます。
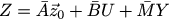
わかった 今、私たちは何が欲しいですか? 補正項y_kを小さくし、そのz_kをx_kに収束させます。
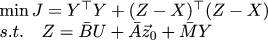
前回と同様に、ZからYまでを表現し、Yに関する偏導関数をゼロに等しくし、最適な補正項の式を取得します。
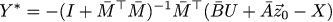
それから漠然とした予感は私を苦しめ始めます...どこかで私はすでにそれを見ました! さて、XとUの関係を思い出しましょう。次の式が得られます。
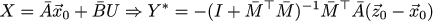
しかし、これは、文字の名前を変更するまで、U *の表現です! 実際、少し戻って、早急に行動に移しました。 x_kのダイナミクスとz_kのダイナミクスを組み合わせると、エラーx_k-z_kのダイナミクスが得られます。
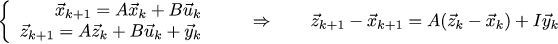
つまり、マシンを追跡するタスクは、線形2次コントローラーのタスクとまったく同じです。 この場合、[[-0.594、-0.673]、[-0.079、-0.774]]に等しい最適なゲイン行列を見つけ、次のオブザーバーコードを取得します。
for i in range(N): Zi = Z[i*n:(i+1)*n,0] Xi = X[i*n:(i+1)*n,0] Z[(i+1)*n:(i+2)*n,0] = A*Zi + B*U[i*m:(i+1)*m,0] + np.matrix([[-0.594,-0.673],[-0.079,-0.774]])*(Zi-Xi)
しかし、フィルタリングされた曲線は不完全ですが、低解像度の測定よりも現実に近いものです。
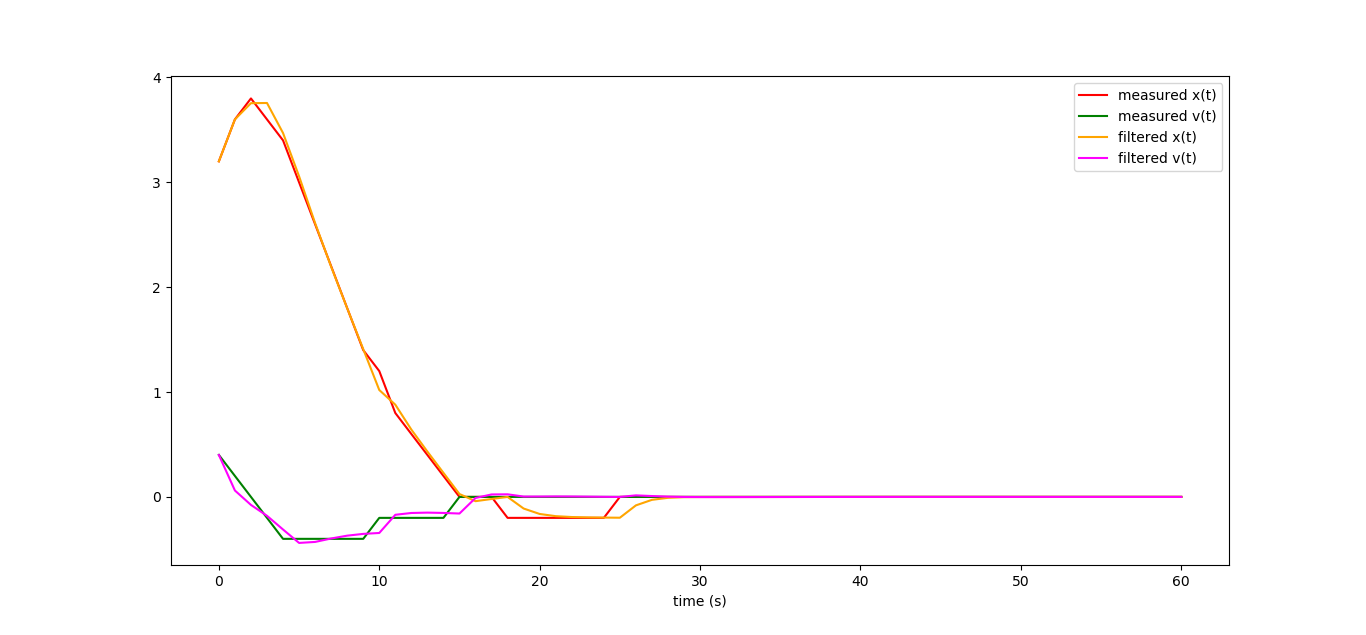
システムのダイナミクスは、行列[[1-0.594.1-0.673]、[-0.079.1-0.774]]の固有値によって決定され、これは(0.316 +-0.133 i)に等しくなります。
さらに先へ進みましょう。 位置のみを測定でき、センサーの速度は測定できないと仮定しましょう。 この場合、オブザーバーを構築できますか? ここではLQRを超えていますが、それほど遠くはありません。 次のシステムを書きましょう。
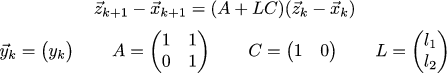
Matrix Cは、システムで実際に観察できることを規定しています。 私たちの仕事は、オブザーバーがうまく振る舞うことを可能にする行列Lを見つけることです。 オブザーバーの一般的なダイナミクスを表す行列A + LCの固有値は、前の例の行列の固有値とほぼ同じである必要があることを手で書きましょう。 前の固有値を分数(1/3 +-1/6 i)で近似してみましょう。 行列A + LCの特性多項式を書き、それを多項式(x-(1/3 + 1/6 * i))*(x-(1 / 3-1 / 6 6 * i)と等しくします。次に、最も単純なシステムを線形方程式、および行列Lが見つかりました。
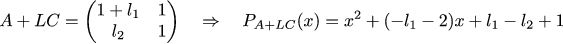
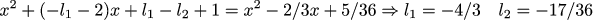
ここで計算をチェックし、ここでグラフの描画を取ることができ ます 。
これは、マシンの座標のみを測定する(そして大きな誤差を伴う)場合、観測者の作業のグラフがどのように見えるかです。
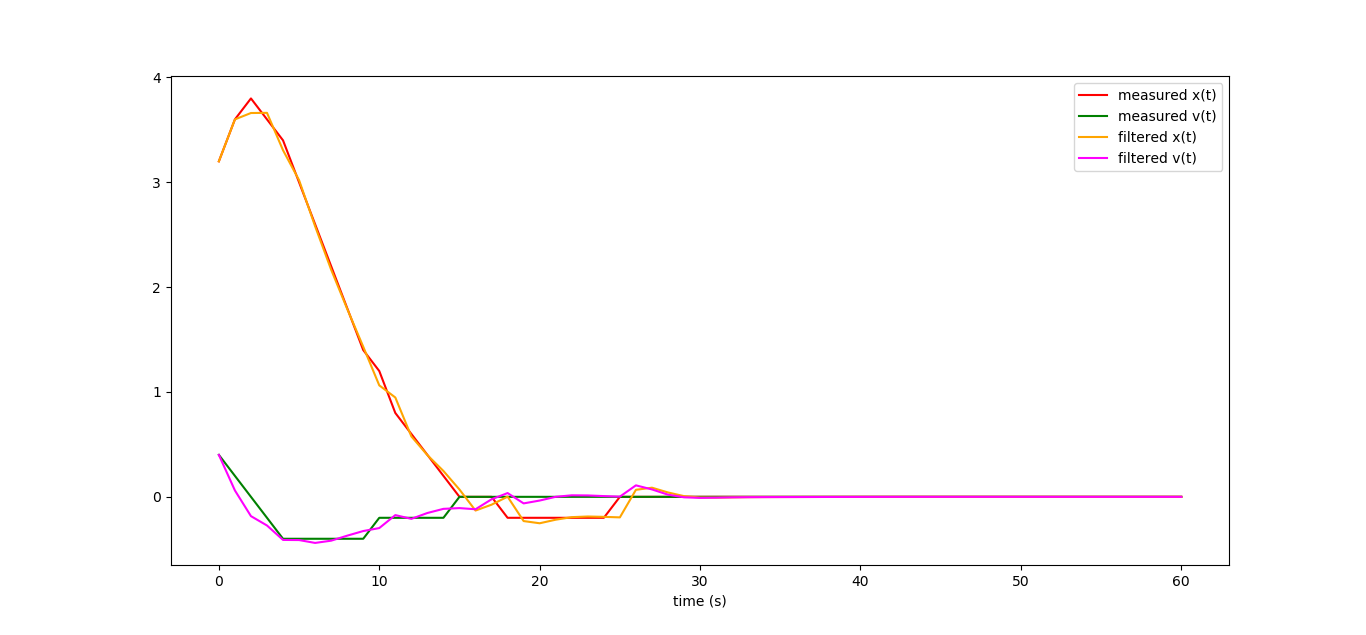
非常に不完全なデータから、システム全体のダイナミクスを非常にうまく復元できます! ちなみに、実際に作成した線形観測器は有名なカルマンフィルターですが、次回はそれについて説明します。
注意深い読者への質問
それでも、Y *が論理的な終わりになった場合(ここでコードを取り上げます) 、結果のオブザーバーカーブは、それらに相当するはずのカーブよりもはるかに滑らかです(そして、真実により近い!)。 なんで?