独自の物理2Dエンジンを作成します：パート2-4

目次

パート2：エンジンコア

• 統合
• タイムスタンプ
• モジュラーアーキテクチャ
  • 本体
  • フォーム
  • 力
  • 素材
• 広い位相
  • 重複する連絡先ペアのクリッピング
  • レイヤーシステム
• 半空間の交点を確認する

パート3：摩擦、シーン、および遷移表

• 摩擦
• シーン
• 衝突遷移表

パート4：指向性ソリッド

• 数学回転
• オリエンテッドフォーム
• 衝突認識
• 衝突解決

---

パート2：エンジンコア

記事のこのパートでは、力パルスの分解能に他の機能を追加します。 特に、統合、タイムスタンプ、コードでのモジュラーアーキテクチャの使用、および広いフェーズでの衝突検出を検討します。

---

はじめに

前の投稿で、 力パルスの解決のトピックを調べました。 まだ読んでいない場合は最初に読んでください！



この記事で取り上げるトピックを掘り下げてみましょう。 これらすべてのトピックは、多かれ少なかれ価値のある物理エンジンに必要であるため、前の投稿で築いた基盤の上に新しい機能を作成するときが来ました。

• 統合
• タイムスタンプ
• モジュラーアーキテクチャ
  • 本体
  • フォーム
  • 力
  • 素材
• 広い位相
  • 重複する連絡先ペアのクリッピング
  • レイヤーシステム
• 半交差チェック

---

統合

統合は非常に簡単に実装でき、インターネット上の反復統合に関する多くの情報があります。 このセクションでは、主に適切な統合の機能に注目し、興味があればより詳細な情報を見つけることができる場所を説明します。



まず、加速とは何かを理解する必要があります。 ニュートンの第二法則は次のように述べています。

$$

$$方程式\：1：\\ F = ma$$

彼は、物体に作用するすべての力の合計は、この物体の質量m



に加速度a



掛けたものに等しいと主張してa



ます。 m



キログラム、a-メートル/ s、 F



ニュートンm



示されます。



a



を計算a



ための方程式をわずかに変換し、以下を取得します。

$$

$$方程式\：2：\\ a = \ frac {F} {m} \\ \したがって、\\ a = F * \ frac {1} {m}$$

次のステップでは、オブジェクトをある場所から別の場所に移動するために加速します。 ゲームはアニメーションの錯覚を作り出す個別のフレームに表示されるため、これらの個別のステップの各位置の位置を計算する必要があります。 これらの方程式のより詳細な分析については、 Erin CattoのGDC 2009との統合デモおよびHannのオイラーのシンプレクティック法の補足を参照して、低FPS環境での安定性を高めてください。



オイラーの方法による明示的な統合を次のコードフラグメントに示します。ここで、 x



は位置、 v



は速度です。 上で説明したように、 1/m * F



は加速度であることに注意してください。

 //    x += v * dt v += (1/m * F) * dt
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここでのdt



は、時間のデルタ（増加）を示します。 Δはデルタ記号であり、文字通り「大きさの変化」と読むか、 t



書くことができます。 したがって、 dt



を見ると、「時間の変化」と読むことができます。 dv



は「速度の変更」です。



このシステムは機能し、通常は出発点として使用されます。 ただし、数値の不正確さがあり、不必要なトラブルなしに除去できます。 以下は、シンプレクティックオイラー法と呼ばれるアルゴリズムです。

 //    v += (1/m * F) * dt x += v * dt
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

2行のコードの順序を変換したばかりであることに注意してください。 上記のHannahの記事を参照してください。



この投稿では、明示的なオイラー法の数値の不正確さについて説明しますが、ハンヌはRK4の検討を開始していることに注意してください。



これらの単純な方程式は、線形の速度と加速度ですべてのオブジェクトを移動するのに十分です。

---

タイムスタンプ

ゲームは個別の時間間隔で表示されるため、これらのステップ間で制御された方法で時間を操作する方法が必要です。 異なるコンピューターで異なる速度で実行されるゲームを見たことがありますか？ これは、コンピューターの能力に応じた速度で実行されるゲームの例です。



物理エンジンが一定の時間を経過した後にのみ実行されることを保証する方法が必要です。 したがって、計算で使用されるdt



は常に同じ数のままです。 コードのどこでも正確な定数値dt



を使用すると、物理エンジンは決定論的なものに変わり、このプロパティは一定のタイムスタンプとして知られています。 これは非常に便利なことです。



決定論的物理エンジンは、同じ入力で常に同じことを行うエンジンです。 これは、ゲームプレイを物理エンジンの動作に明確に結び付ける必要がある多くの種類のゲームで必要です。 さらに、エンジンの動作のエラーを検出するためには、エンジンを変更する必要がないため、エンジンをデバッグする必要があります。



始めるために、一定のタイムスタンプの単純なバージョンを見てみましょう。 以下に例を示します。

 const float fps = 100 const float dt = 1 / fps float accumulator = 0 //   -  float frameStart = GetCurrentTime( ) //   while(true) const float currentTime = GetCurrentTime( ) //  ,      accumulator += currentTime - frameStart( ) //     frameStart = currentTime while(accumulator > dt) UpdatePhysics( dt ) accumulator -= dt RenderGame( )
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このコードは、物理を更新するのに十分な時間が経過するまで待機し、ゲームをレンダリングします。 経過時間が記録され、 dt



サイズの離散時間ブロックがアキュムレーターから取得され、物理学によって処理されます。 これにより、すべての条件で同じ値が物理に送信され、物理に送信される値が実際の生活で経過した実際の時間を正確に反映することが保証されます。 accumulator



がdt



ブロックより小さくなるまで、 dt



ブロックはaccumulator



から削除されます。



ここで、いくつかの問題を修正できます。 1つ目は、物理学の更新に必要な時間に関連しています。物理学の更新に時間がかかりすぎて、ゲームサイクルごとにaccumulator



が増えるとどうなりますか。 これは「死のスパイラル」と呼ばれます。 この問題が解決されない場合、物理学の計算が十分に速くなければ、エンジンはすぐに完全に停止します。



この問題を解決するために、 accumulator



が大きくなりすぎた場合、エンジンは物理的な更新を少なくする必要があります。 これを行う最も簡単な方法の1つは、 accumulator



任意の値より大きくならないようにaccumulator



を制限するaccumulator



です。

 const float fps = 100 const float dt = 1 / fps float accumulator = 0 //   -  float frameStart = GetCurrentTime( ) //   while(true) const float currentTime = GetCurrentTime( ) //  ,      accumulator += currentTime - frameStart( ) //     frameStart = currentTime //       dt,   //    UpdatePhysics  //   . if(accumulator > 0.2f) accumulator = 0.2f while(accumulator > dt) UpdatePhysics( dt ) accumulator -= dt RenderGame( )
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

さて、このサイクルを実行するゲームが何らかの理由で単純であるとわかった場合、物理学は死のスパイラルに引きずられません。 ゲームの実行速度は少し遅くなります。



次の問題は、死のらせんに比べてはるかに小さいです。 このループは、 accumulator



がdt



未満になるまで、 accumulator



からdt



ブロックを取得します。 これは素晴らしいことですが、 accumulator



まだ少し時間があります。 これが問題です。



accumulator



各フレームがdt



ブロックの1/5のままであるとします。 6番目のフレームでは、 accumulator



に他のすべてのフレームの物理更新を実行するのに十分な残り時間があります。 これにより、1秒あたり約1フレーム程度で、わずかに大きな離散ジャンプが実行され、ゲーム内で非常に顕著になります。



この問題を解決するには、 線形補間を使用する必要があります。 怖いですが、恐れてはいけません-実装を示します。 実装方法を理解したい場合は、インターネット上に線形補間専用の多くのリソースがあります。

 //    a  0  1 //  t1  t2 t1 * a + t2(1.0f - a)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このコードを使用すると、2つの異なる時間間隔の間にある可能性のある場所を補間（概算）できます。 この位置を使用して、2つの物理更新間のゲームの状態をレンダリングできます。



線形補間を使用すると、物理エンジンとは異なる速度でエンジンをレンダリングできます。 これにより、物理更新からaccumulator



の残りをエレガントに処理できます。



完全な例を次に示します。

 const float fps = 100 const float dt = 1 / fps float accumulator = 0 //   -  float frameStart = GetCurrentTime( ) //   while(true) const float currentTime = GetCurrentTime( ) //  ,      accumulator += currentTime - frameStart( ) //     frameStart = currentTime //       dt,   //    UpdatePhysics  //   . if(accumulator > 0.2f) accumulator = 0.2f while(accumulator > dt) UpdatePhysics( dt ) accumulator -= dt const float alpha = accumulator / dt; RenderGame( alpha ) void RenderGame( float alpha ) for shape in game do //      Transform i = shape.previous * alpha + shape.current * (1.0f - alpha) shape.previous = shape.current shape.Render( i )
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

したがって、ゲーム内のすべてのオブジェクトは、物理学の個別のタイムスタンプの間のさまざまな時点で描画できます。 これにより、すべてのエラーをエレガントに処理し、残りの時間を蓄積できます。 実際、レンダリングは計算された物理学よりも少し遅れて実行されますが、ゲームを観察すると、すべての動きが補間によって著しく滑らかになります。



プレイヤーは、自分が見ているものだけを知っているので、レンダリングが常に物理学に遅れていると推測することはありません。また、あるフレームから別のフレームへの完全に滑らかな遷移を見るからです。



不思議に思うかもしれません：なぜ現在の位置から次の位置まで補間しないのですか？ 私はこれをしようとしましたが、これには、オブジェクトが将来存在する場所を「推測」するレンダリングが必要であることがわかりました。 物理エンジン内のオブジェクトは、たとえば衝突中に突然動きを変更することが多く、そのような突然の変更が発生すると、オブジェクトは将来の不正確な補間により別の場所にテレポートされます。

---

モジュラーアーキテクチャ

各物理オブジェクトには、いくつかのプロパティが必要です。 ただし、特定の各オブジェクトのパラメーターはわずかに異なる場合があります。 このすべてのデータを整理するスマートな方法が必要です。そのような配置では、できるだけ少ないコードを書くことをお勧めします。 この場合、モジュラーアーキテクチャがあります。



「モジュール式アーキテクチャ」というフレーズは哀れで複雑すぎるように聞こえるかもしれませんが、実際には非常に論理的で非常に単純です。 これに関連して、「モジュールアーキテクチャ」とは、物理オブジェクトを便利な方法で接続および切断できるように、物理オブジェクトを個別の部分に分割できることを意味します。

本体

肉体は、特定の肉体に関するすべての情報を含むオブジェクトです。 オブジェクトを構成するフォーム（複数可）、質量、変換（位置、回転）、速度、トルクなどのデータを保存します。 ボディは次のようになります。

 struct body { Shape *shape; Transform tx; Material material; MassData mass_data; Vec2 velocity; Vec2 force; real gravityScale; };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これは、身体の構造を作成するための素晴らしい出発点です。 ここでは、適切なコード構造を作成するために論理的な決定が行われます。



まず、フォームがポインターを使用して本文に配置されることは注目に値します。 これにより、体とその形状の間に弱いつながりが作成されます。 ボディには任意の形状を含めることができ、ボディの形状は任意に変更できます。 実際、ボディはいくつかの形式で表すことができ、そのようなボディはいくつかの形式で構成されているため、「複合」と呼ばれます。 （このチュートリアルでは、複合ボディは考慮しません。）





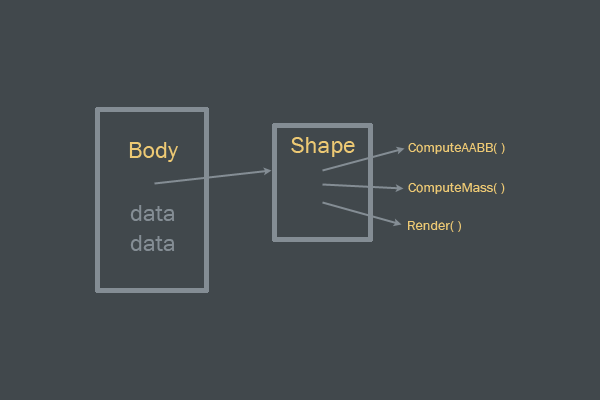
本体とフォームのインターフェース。



shape



自体は、境界形状の計算、密度に基づく質量の計算、およびレンダリングを担当します。



mass_data



は、質量関連情報を保存するための小さなデータ構造です。

 struct MassData { float mass; float inv_mass; //   (  ) float inertia; float inverse_inertia; };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

質量と慣性に関連するすべての値を単一の構造に保存すると非常に便利です。 質量は決して手動で設定しないでください-質量は常にフォーム自体から計算する必要があります。 質量はやや直感に反する値タイプであり、手動で設定するには微調整に時間がかかります。 次のように定義されます。

$$

$$式3：\\質量=密度*体積$$

デザイナーがフォームをより「大」または「重」にする必要がある場合、フォームの密度を変更する必要があります。 この密度は、体積を使用してフォームの質量を計算するために使用できます。 これは、密度が音量の影響を受けず、ゲームの実行中に変化しないため（特別なコードが提供されていない限り）、このような状況で動作する正しい方法です。



AABBや円などの形状の例は、チュートリアルの前の部分で見つけることができます。

素材

質量と密度に関するこのすべての話から、密度値はどこに保存されているのかという疑問が生じます。 Material



構造にあります：

 struct Material { float density; float restitution; };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

マテリアル値を設定した後、このマテリアルをボディシェイプに転送して、ボディが質量を計算できるようにすることができます。



最後に言及する価値があるのはgravity_scale



です。 さまざまなオブジェクトの重力のスケーリングは、ゲームプレイを微調整するときに非常に役立つことが多いため、このタスク専用にこの値を各ボディに追加する価値があります。



最も一般的なマテリアルの便利な設定を使用して、 Material



オブジェクトの列挙値を作成できます。

 Rock Density : 0.6 Restitution : 0.1 Wood Density : 0.3 Restitution : 0.2 Metal Density : 1.2 Restitution : 0.05 BouncyBall Density : 0.3 Restitution : 0.8 SuperBall Density : 0.3 Restitution : 0.95 Pillow Density : 0.1 Restitution : 0.2 Static Density : 0.0 Restitution : 0.4
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

力

body



構造の別の側面を議論する必要があります。 これはforce



と呼ばれるデータ項目です。 各物理の更新の開始時、この値はゼロです。 物理エンジンの他の効果（重力など）は、このforce



データ要素にVec2



ベクトルを追加します。 統合の直前に、これらの力はすべて、身体の加速度を計算するために使用され、統合段階で適用されます。 統合後、このforce



データ項目はリセットされます。



これにより、任意の数の力でオブジェクトに作用でき、新しいタイプの力をオブジェクトに適用するために、新しいコードを記述する必要がなくなります。



例を見てみましょう。 非常に重いオブジェクトである小さな円があるとします。 この小さな円はゲームの世界を飛び回り、非常に重いため、他のオブジェクトを常に少しずつ引き寄せています。 これを示すための粗い擬似コードを次に示します。

 HeavyObject object for body in game do if(object.CloseEnoughTo( body ) object.ApplyForcePullOn( body )
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ApplyForcePullOn()



関数は、 body



が十分に近い場合にのみ、 body



をHeavyObject



引っ張る小さな力を指します。









2つのオブジェクトが、それらを通り過ぎる大きなオブジェクトに引き付けられました。 引力は、大きな長方形までの距離に依存します。



身体のforce



どれだけの力がかかるかは関係ありません。なぜなら、それらはこの身体の単一の共通ベクトルに合計されるからです。 これは、1つの身体に作用する2つの力が潜在的に相互にバランスを取ることができることを意味します。

---

広い位相

シリーズの前回の記事では、衝突認識手順を紹介しました。 これらの手順は、実際には「狭相」と呼ばれるものとは無関係です。 広いフェーズと狭いフェーズの違いは、Googleで簡単に見つけることができます。



（要するに、衝突の可能性があるオブジェクトのペアを決定するために、幅広い衝突認識フェーズを使用し、次に、衝突するかどうかを確認するために狭い衝突認識フェーズを使用します。）



時間の複雑さを持つアルゴリズムのペアを計算する幅広いフェーズを実装する方法を説明するコード例を示したい $$$O（n ^ 2）$ 。



$$$O（n ^ 2）$ 潜在的な衝突の各ペアのチェックに費やされる時間は、オブジェクトの数の2乗に依存することを意味します。 「O」bigという表記を使用します。



オブジェクトのペアを扱うため、同様の構造を作成すると便利です。

 struct Pair { body *A; body *B; };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

広いフェーズでは、起こりうる衝突のグループを組み立て、それらをすべてPair



構造に格納します。 その後、これらのペアをエンジンの別の部分（狭位相）に転送して、後続の解決策を実行できます。



幅広いフェーズの例：

 //   . //        . void BroadPhase::GeneratePairs( void ) { pairs.clear( ) //    AABB,    //       AABB A_aabb AABB B_aabb for(i = bodies.begin( ); i != bodies.end( ); i = i->next) { for(j = bodies.begin( ); j != bodies.end( ); j = j->next) { Body *A = &i->GetData( ) Body *B = &j->GetData( ) //      if(A == B) continue A->ComputeAABB( &A_aabb ) B->ComputeAABB( &B_aabb ) if(AABBtoAABB( A_aabb, B_aabb )) pairs.push_back( A, B ) } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

上記のコードは非常に単純です。すべてのボディを他のすべてのボディとチェックし、それ自体との衝突のチェックをスキップします。

重複のクリッピング

最後のセクションには1つの問題があります。多くの重複ペアが返されます。 これらの重複は結果から削除する必要があります。 並べ替えライブラリが手元にない場合は、並べ替えアルゴリズムに精通している必要があります。 C ++で記述している場合は、幸運です。

 //      sort( pairs, pairs.end( ), SortPairs ); //       { int i = 0; while(i < pairs.size( )) { Pair *pair = pairs.begin( ) + i; uniquePairs.push_front( pair ); ++i; //  ,  ,      while(i < pairs.size( )) { Pair *potential_dup = pairs + i; if(pair->A != potential_dup->B || pair->B != potential_dup->A) break; ++i; } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

特定の順序ですべてのペアを並べ替えた後、 pairs



コンテナー内のすべてのペアが近傍で重複していると想定できます。 すべての一意のペアを新しいuniquePairs



コンテナーに配置します。これは、重複を切り取る作業です。



最後に言及する価値があるのは、 SortPairs()



述語です。 この関数SortPairs()



ソートに使用されます。 次のようになります。

 bool SortPairs( Pair lhs, Pair rhs ) { if(lhs.A < rhs.A) return true; if(lhs.A == rhs.A) return lhs.B < rhs.B; return false; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

lhs



およびrhs



メンバーは、「左側」（左側）および「右側」（右側）として復号化できます。 これらのメンバーは通常、要素を方程式またはアルゴリズムの左右の部分と論理的に見なすことができる関数のパラメーターを操作するために使用されます。

レイヤーシステム

異なるオブジェクトが互いに衝突しないように、 レイヤーシステムが必要です。 特定のオブジェクトから飛んでくる弾丸が他の特定のオブジェクトに影響を与えないようにする必要があります。 たとえば、同じチームのミサイルを持つプレイヤーは敵にダメージを与えるべきですが、お互いにダメージを与えるべきではありません。









レイヤーシステムの説明：一部のオブジェクトは互いに衝突しますが、他のオブジェクトは衝突しません。



レイヤーシステムはビットマスクを使用して最もよく実装されます 。 エンジンでのビットマスクの使用方法については、 プログラマ向けビットマスクの簡単な紹介 、Wikipediaページ、および参考のためにBox2Dマニュアルのフィルタリングセクションを参照してください。



層システムは、幅広いフェーズで実装されます。 ここでは、既成の広いフェーズの例を挿入します。

 //   . //        . void BroadPhase::GeneratePairs( void ) { pairs.clear( ) //    AABB,    //       AABB A_aabb AABB B_aabb for(i = bodies.begin( ); i != bodies.end( ); i = i->next) { for(j = bodies.begin( ); j != bodies.end( ); j = j->next) { Body *A = &i->GetData( ) Body *B = &j->GetData( ) //      if(A == B) continue //     if(!(A->layers & B->layers)) continue; A->ComputeAABB( &A_aabb ) B->ComputeAABB( &B_aabb ) if(AABBtoAABB( A_aabb, B_aabb )) pairs.push_back( A, B ) } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

レイヤーシステムは非常に効率的で非常にシンプルです。

---

半空間の交差点

半空間は、2Dでは直線の片側と見なすことができます。ポイントが直線の片側にあるか反対側にあるかを判断することはかなり一般的なタスクであり、独自の物理エンジンを実装するときは、それをよく理解する必要があります。私には、このトピックがインターネット上のどこにも詳細に開示されていないのは非常に悪いことであり、私たちはそれを修正します！



2Dの線の一般的な方程式は次のとおりです。

$$

$$\: 4:\\ \: : ax + by + c = 0\\ \: \: : \begin{bmatrix} a \\ b \\ \end{bmatrix}$$

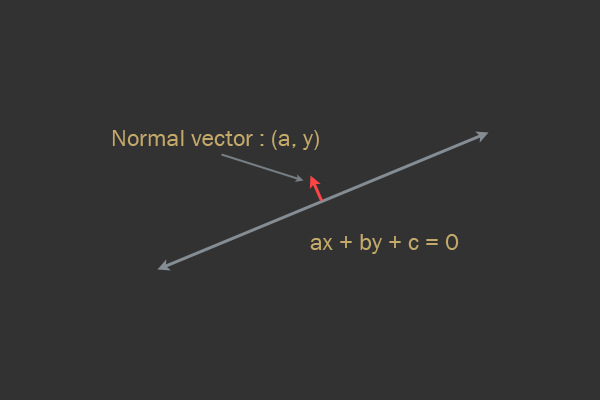
その名前にもかかわらず、法線ベクトルは必ずしも正規化されるとは限らないことに注意してください（つまり、必ずしも長さが1であるとは限りません）。



ポイントがラインの特定の側にあるかどうかを判断するには、変数x



とy



方程式のポイントを置き換えて、結果の符号を確認するだけです。結果が0の場合、ポイントは線上にあり、正/負の値は線の異なる側を意味します。



そしてそれだけです！これを知っているのは、ポイントからラインまでが以前のチェックの結果です。法線ベクトルが正規化されていない場合、結果は法線ベクトルの大きさでスケーリングされます。

---

おわりに

この時点で、非常に単純ではありますが、完全な物理エンジンをゼロから作成できます。次のパートでは、より複雑なトピックを扱います：摩擦：方向、およびAABB動的ツリー。

パート3：摩擦、シーン、および遷移表

記事のこの部分では、次のトピックを検討します。

• 摩擦
• シーン
• 衝突遷移表

---

ビデオデモ

このパートで取り組む内容の簡単なデモを次に示します。

---

摩擦

摩擦は衝突解決システムの一部です。摩擦は、オブジェクトの動きとは反対の方向にオブジェクトに適用される力に常に適用されます。



実際には、摩擦は異なる物質間の非常に複雑な相互作用であり、それをモデル化するために深刻な仮定と近似が行われます。これらの仮定は数学に関連しており、通常、ほぼ次のように定式化されます：「摩擦はほぼ1つのベクトルとして表すことができます」



記事の最初の部分のビデオデモをご覧ください。





身体間の相互作用は非常に興味深いものであり、衝突時の反発は現実的に見えます。ただし、オブジェクトが固定プラットフォームに着地すると、それらはすべて反発し、画面の端から滑り落ちるように見えます。これは、摩擦のシミュレーションがないためです。

再び力の衝動？

おそらくチュートリアルの最初の部分で覚えているように、衝突における2つのオブジェクトの貫通を分離するにj



は、力の運動量の大きさを表す値が必要です。この値は、衝突の法線に沿って速度を変更するために使用されるため、jnormal



またはとして指定できますjN



。



摩擦反応を追加するには、jtangent



またはとして示される別の量を計算する必要がありますjT



。摩擦は力の衝撃としてモデル化できます。この値は、負の接線衝突ベクトルに沿って、つまり摩擦ベクトルに沿ってオブジェクトの速度を変更します。 2次元では、摩擦ベクトルの計算は解決可能なタスクですが、3Dでははるかに複雑になります。



摩擦は非常に単純であり、前の方程式を再び使用できます。j



すべての法線n



を接線ベクトルに置き換えますt



。

$$

$$\: 1:\\ j = \frac{-(1 + e)(V^{B}-V^{A})\cdot n)} {\frac{1}{mass^A} + \frac{1}{mass^B}}$$

置き換えn



にt



：

$$

$$\:2:\\ j = \frac{-(1 + e)((V^{B}-V^{A})\cdot t)} {\frac{1}{mass^A} + \frac{1}{mass^B}}$$

この方程式でt



は1つの出現のみが置換されますがn



、回転を追加した後、方程式2の分子内の出現を除いて、さらにいくつかの出現を置換する必要があり



ますt



。接線ベクトルは、衝突の法線に垂直なベクトルであり、法線により近い方向に向けられます。これは混乱を招く可能性があります-心配しないでください、図面があります！



次の図は、接線ベクトルが法線に垂直であることを示しています。接線ベクトルは、左または右に向けることができます。左にある場合、相対速度から「さらに」離れています。ただし、それは法線に垂直で、相対速度に「近い」方向として定義されます。









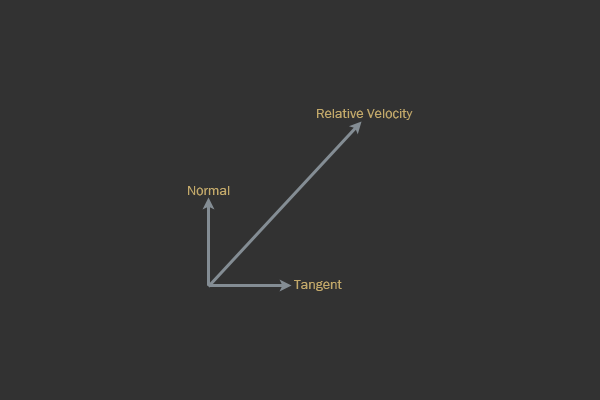
固体の衝突の時間枠内のさまざまなタイプのベクトル。



上で簡単に説明したように、摩擦は接線ベクトルと反対方向に向けられたベクトルになります。これは、法線ベクトルが衝突を認識するため、摩擦を適用する方向を直接計算できることを意味します。



これがわかっている場合、接線ベクトルは次のようになります（n



衝突の法線はどこですか）。

$$

$$V^R = V^{B}-V^{A} \\ t = V^R - (V^R \cdot n) * n$$

摩擦の量を決定するにはjt



、上記の式から値を直接計算するだけです。すぐにこの値を計算した後に他のトリックを検討するため、衝突の解決に必要なのはこれだけではありません。

 //      //   (    ,     //      ) Vec2 rv = VB - VA //    Vec2 tangent = rv - Dot( rv, normal ) * normal tangent.Normalize( ) //  ,     float jt = -Dot( rv, t ) jt = jt / (1 / MassA + 1 / MassB)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

上記のコードは式2に直接対応します。ここでも、摩擦ベクトルが接線ベクトルと反対方向を指していることを理解することが重要です。したがって、接線ベクトルに沿った相対速度を計算するために、相対速度のスカラー積が接線方向である場合、マイナス記号を追加する必要があります。マイナス記号は接線速度を反転させ、摩擦が近似されるべき方向を突然示します。

アモントン-クーロンの法則

アモントン-クーロンの法則は、ほとんどのプログラマーが困難を感じる摩擦シミュレーションの一部です。私自身は、適切なモデリング手法を見つけるのに十分な時間をかけて研究しなければなりませんでした。秘Theは、アモントン・クーロンの法則が不平等であることです。



それは読みます：

$$

$$\:3: \\ F_f <= \mu F_n$$

言い換えれば、摩擦力は常に法線力に一定の定数を掛けμ



た値以下です（その値はオブジェクトの材料によって異なります）。



通常の強さは、単に古い値j



に衝突の法線を掛けたものです。そのため、計算されたjt



（摩擦力を表す）がμ



一度に法線力よりも小さい場合は、値jt



を摩擦として使用できます。そうでない場合は、代わりに法線力にを掛けた値を使用する必要がありますμ



。この「if」条件は、摩擦をある最大値に制限します。最大値は法線力の時間μ



です。



アモントン・クーロンの法則の要点は、この制限手順を実行することです。このような制限は、力のインパルスに基づいた解像度の摩擦シミュレーションの最も難しい部分であることが判明しました-それに関するドキュメントはどこにもありませんが、今すぐ修正します！私がこのトピックで見つけた記事の大部分では、摩擦は完全に破棄されるか簡単に言及され、制限手順は正しく実装されていません（またはまったく存在しません）。この部分を適切に理解することが非常に重要であることを理解してください。



何かを説明する前に、制限を完全に実装しましょう。以下のコードブロックは、既製の制限手順と摩擦力のインパルスの適用を含む前の例です。

 //      //   (    ,     //      ) Vec2 rv = VB - VA //    Vec2 tangent = rv - Dot( rv, normal ) * normal tangent.Normalize( ) //  ,     float jt = -Dot( rv, t ) jt = jt / (1 / MassA + 1 / MassB) // PythagoreanSolve = A^2 + B^2 = C^2,  C   A  B //           float mu = PythagoreanSolve( A->staticFriction, B->staticFriction ) //         Vec2 frictionImpulse if(abs( jt ) < j * mu) frictionImpulse = jt * t else { dynamicFriction = PythagoreanSolve( A->dynamicFriction, B->dynamicFriction ) frictionImpulse = -j * t * dynamicFriction } //  A->velocity -= (1 / A->mass) * frictionImpulse B->velocity += (1 / B->mass) * frictionImpulse
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この式を使用して、各ボディに指定された係数で2つのボディ間の摩擦係数を決定することにしました。

$$

$$\:4: \\ Friction = \sqrt[]{Friction^2_A + Friction^2_B}$$

実際、私はすでに誰かが自分の物理エンジンでそれをどのように使用しているかを見てきましたが、結果が気に入りました。平方根を取り除く必要がある場合、2つの値の平均は完璧です。実際、摩擦係数の任意の形式の選択が機能しますが、私はこれを好むだけです。別のオプション：検索テーブルを使用できます。この場合、各ボディのタイプは2次元テーブルのインデックスです。



比較jt



では絶対値を使用することが重要です。理論的には、比較により「生の」値が何らかのしきい値に制限されるためです。ようにj



常に正である、動摩擦の場合の摩擦の真のベクトルを表すように、逆にされなければなりません。

静的および動的摩擦

前のコードスニペットでは、静的摩擦と動的摩擦が説明なしで導入されました。これらの2つのタイプの値の違いと必要性の違いを説明するために、セクション全体を捧げます。



摩擦の間、興味深いことが起こります。オブジェクトが静止状態から動きに移動するには、「活性化エネルギー」が必要です。実際の生活で2つのオブジェクトが重なり合っている場合、1つを押して動かすにはかなりのエネルギーが必要です。ただし、オブジェクトを異なる方法でスライドさせた場合、多くの場合、その後のグライドを維持するために必要なエネルギーは少なくなりました。



これは、顕微鏡レベルでの摩擦の原理によるものです。別の図がここで役立ちます。









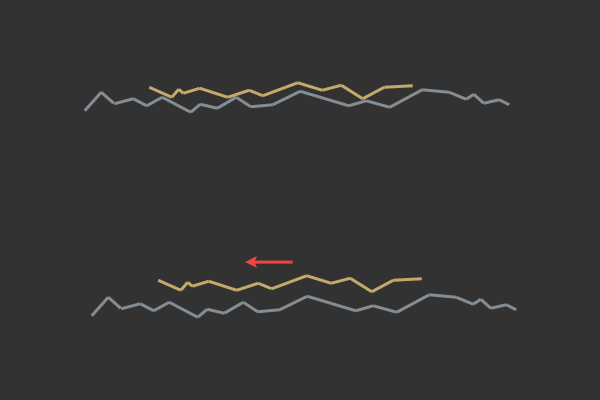
摩擦中の活性化エネルギーの必要性の微視的理由。



ご覧のとおり、実際、摩擦を引き起こす主な障害は、サーフェス間の小さなバンプです。あるオブジェクトが別のオブジェクトの上にある場合、オブジェクト間で微視的な不規則性が静止し、それらをリンクします。この接続は、オブジェクトを相互にスライドできるように、分割または分割する必要があります。



エンジン内でこれをシミュレートする方法を見つける必要があります。最も簡単な解決策は、各タイプの材料に2つの摩擦値を与えることです。1つは静的、もう1つは動的です。



静摩擦は、大きさを制限するために使用されますjt



。場合、数量を計算するときjt



小さすぎることがわかり（しきい値を下回っている）、オブジェクトが静止している、またはそれに近いと仮定し、値全体jt



を力のインパルスとして使用できます。



一方、計算のjt



値がしきい値よりも高い場合、オブジェクトが既に「活性化エネルギー」を超えていると想定できます。この状況では、摩擦力のより低い運動量が使用されます。これは、より低い摩擦係数と力の運動量のわずかに異なる計算で表されます

---

シーン

「摩擦」のセクションを注意深く読んだら、おめでとうございます！チュートリアル全体の中で最も難しい（私の意見では）部分を完了しました。



このクラスはScene



、物理シミュレーションシナリオに関連するすべてのコンテナとして使用されます。すべての広範なフェーズの結果を呼び出して使用し、すべてのソリッドを含み、衝突チェックを実行し、その解決を呼び出します。また、すべてのアクティブなオブジェクトを結合します。また、シーンはユーザー（たとえば、物理エンジンを使用するプログラマー）と対話します。



シーンの構造がどのように見えるかの例を次に示します。

 class Scene { public: Scene( Vec2 gravity, real dt ); ~Scene( ); void SetGravity( Vec2 gravity ) void SetDT( real dt ) Body *CreateBody( ShapeInterface *shape, BodyDef def ) //        ( ). void InsertBody( Body *body ) //     void RemoveBody( Body *body ) //      void Step( void ) float GetDT( void ) LinkedList *GetBodyList( void ) Vec2 GetGravity( void ) void QueryAABB( CallBackQuery cb, const AABB& aabb ) void QueryPoint( CallBackQuery cb, const Point2& point ) private: float dt //     float inv_dt // ,      LinkedList body_list uint32 body_count Vec2 gravity bool debug_draw BroadPhase broadphase };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

教室にScene



特に複雑なものはありません。このアイデアは、ユーザーが便利にソリッドを追加および削除できるようにすることです。BodyDef



-これは、ソリッドに関するすべての情報を含む構造であり、ユーザーが構成構造のようなものに値を挿入するために使用できます。



もう1つの重要な機能はStep()



です。この関数は、衝突チェック、解決、統合の1ステップを実行します。チュートリアルの第2部で作成されたタイムスタンプのサイクルから呼び出す必要があります。



ポイントまたはAABBが要求されると、シーン内で実際にポイントまたはAABBと衝突するオブジェクトを確認します。このゲームプレイ関連のロジックのおかげで、オブジェクトが世界でどのように配置されているかを簡単に理解できます。

---

変換表

2つの異なるオブジェクトのタイプに応じて、呼び出された衝突関数を選択する簡単な方法が必要です。



C ++では、2つの主要な方法を知っています。ダブルディスパッチ（ダブルディスパッチ）と2次元遷移テーブルです。私のテストでは、2次元テーブルが最適であることがわかったため、その実装を詳細に検討します。非Cおよび非C ++を使用する予定の場合、関数ポインタのテーブルと同様に、関数または機能オブジェクトの配列を作成できることは確かです（これはC ++に固有の他のオプションではなく、遷移テーブルを選択するもう1つの理由です）



CまたはC ++のジャンプテーブルは、関数ポインタのテーブルです。任意の名前または定数であるインデックスは、テーブルのインデックスとして使用され、特定の関数を呼び出します。1次元のジャンプテーブルを使用すると、次のようになります。

 enum Animal { Rabbit Duck Lion }; const void (*talk)( void )[] = { RabbitTalk, DuckTalk, LionTalk, }; //         talk[Rabbit]( ) //   RabbitTalk
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

上記のコードは、実際にC ++言語自体が実装するものを模倣してい



ます。ただし、C ++では、仮想関数の1次元呼び出しのみが実装されます。2次元テーブルは手動で作成できます。



衝突手順を呼び出すための2次元ジャンプテーブルの擬似コードは次のとおりです。

 collisionCallbackArray = { AABBvsAABB AABBvsCircle CirclevsAABB CirclevsCircle } //        //   A and B,       //    AABB   collisionCallbackArray[A->type][B->type]( A, B )
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そしてそれだけです！各コライダーの真のタイプは、2次元配列のインデックスおよび衝突を解決する関数の選択として使用できます。



ただし、AABBvsCircle



それらCirclevsAABB



が重複していることは注目に値します。両方の機能が必要です！これらの関数の1つでは、法線を反映する必要があり、これが唯一の違いです。これにより、オブジェクトの組み合わせに関係なく、衝突を正しく解決できます。

---

おわりに

ソリッド用の独自の物理エンジンをゼロから作成することに専念している多くのトピックを既に取り上げました！これまで、衝突解決、摩擦、およびエンジンアーキテクチャを研究してきました。この知識により、多くの高品質の2次元ゲーム用の物理エンジンを作成することはすでに可能です。



次のパートでは、エンジンにとって重要な別のトピック、回転と方向について検討します。指向オブジェクトの相互作用を観察することは非常に興味深く、物理エンジンが必要とする最後の部分です。



回転の解決は非常に簡単ですが、衝突の認識はより困難になります。

パート4：指向性ソリッド

そこで、力のインパルス、核の構造、摩擦の解像度を調べました。チュートリアルのこの最後の部分では、非常に興味深いトピックであるオリエンテーションを明らかにします。



このパートでは、次のトピックについて説明します。

• 数学回転
• オリエンテッドフォーム
• 衝突認識
• 衝突解決

---

コード例

実装の詳細の多くは記事自体に適合しなかったため、C ++エンジンの小さな例を作成し、記事を読みながらソースコードを学習することをお勧めします。





このGitHubリポジトリには、サンプルエンジン自体とVisual Studio 2010プロジェクトが含まれていますが、GitHubでは、ダウンロードしなくてもコードを表示できます。



その他の関連記事

• Philip Differferはリポジトリを分岐して、エンジンのJavaバージョンを作成しました！

---

オリエンテーション数学

2Dでの回転に関連する数学は非常に単純ですが、物理エンジンで価値のあるすべてを作成するには、主題の知識が必要です。ニュートンの第二法則は次のように述べています。

$$

$$\: 1:\\ F = ma$$

特に回転力と角加速度に関連する同様の方程式があります。ただし、これらの方程式を理解する前に、2次元空間でのベクトル積を簡単に説明する価値があります。

ベクターアートワーク

3Dのベクターアートワークはよく知られた操作です。ただし、2Dのベクトル積は、実際には便利な幾何学的解釈を持たないため、非常に紛らわしい場合があります。



2Dのベクトル積は、3Dのバージョンとは異なり、ベクトルではなくスカラーを返します。このスカラー積は、実際にベクトル積が3Dで実行されているかのように、Z軸に沿った直交ベクトルの大きさを実際に決定します。ある意味では、2Dのベクトル積は3Dベクトル数学の拡張であるため、3Dのベクトル積の単純化されたバージョンです。



これで混乱する場合でも、心配しないでください。2次元空間のベクターアートについて深く理解する必要はありません。この操作の実行方法を正確に知り、操作の順序が重要であることを知るだけで十分です。$$a × bは次と同じではありません$a \times b$$$$b \times a$ 。このパートでは、ベクトル積を積極的に使用して角速度を線形に変換します。



ただし、2Dでのベクトル積の実行方法を知ることも非常に重要です。2つのベクトル、スカラーとベクトル、またはベクトルとスカラーのベクトル積を実行できます。操作は次のとおりです。

 //       float CrossProduct( const Vec2& a, const Vec2& b ) { return ax * by - ay * bx; } //   ( )    //   a   s,    Vec2 CrossProduct( const Vec2& a, float s ) { return Vec2( s * ay, -s * ax ); } Vec2 CrossProduct( float s, const Vec2& a ) { return Vec2( -s * ay, s * ax ); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

トルクと角速度

前の部分から知っているように、この方程式は、身体に作用する力と、この身体の質量および加速度との関係を示しています。ローテーションのアナログがあります：

$$

$$\: 2:\\ T = r \: \times \: \omega$$

$$Tはトルクを表します。トルクは回転の力です。$T$



$$rは、重心（CM）からオブジェクト上の特定の点までのベクトルです。$r$$$rは、CMからポイントまでの「半径」と見なすことができます。オブジェクトの各一意のポイントには、独自の値が必要です。$r$$$式2で置き換える r$r$



$$ωはオメガと呼ばれ、回転速度を指します。この比率は、ソリッドの角速度を積分するために使用されます。線速度はソリッドステートCMの速度であることを理解することが重要です。前の部分では、すべてのオブジェクトに回転コンポーネントがなかったため、CMの線速度は体のすべてのポイントの速度と同じでした。方向が追加されると、CMから離れたポイントは、CMに最も近いポイントよりも速く回転します。これは、ボディが回転と移動を同時に行えるようになったため、ボディ上のポイントの速度を見つけるための新しい方程式が必要になることを意味します。彼は、次の式を使用して、体のポイントとそのポイントの速度との関係を理解し​​ます。$\omega$

$$

$$\: 3:\\ \omega = r \: \times v$$

$$vは線速度を表します。線速度を角速度に変換するには、半径のベクトル積を見つける必要があります$v$$$$r$ そして $$$v$ 。



つまり、式3を別の形式に変換できます。

$$

$$\: 4:\\ v = \omega \: \times r$$

前のセクションの方程式は、固体の密度が均一である場合にのみ有効です。不均一な密度は、ソリッドボディの回転と動作に関連するすべての数学を複雑にします。さらに、ソリッドを表すボディがCMにない場合、次を含む計算$$rは完全に揺れます。$r$

慣性

2次元では、オブジェクトは仮想軸Zを中心に回転します。この回転は非常に複雑になる場合があり、オブジェクトの重心からの距離に依存します。細長い棒の質量に等しい質量を持つ円は、棒よりも回転しやすいです。この「回転の複雑さ」の要因は、物体の慣性モーメントとして認識できます。



ある意味では、慣性は物体の回転質量です。慣性が大きいほど、回転させるのが難しくなります。



これを知って、物体の慣性を質量と同じ形式で身体の構造に保存できます。また、慣性の値に逆の値を格納すると同時に、ゼロ除算で正確にすることも論理的です。質量および相互質量の詳細については、前のセクションを参照してください。

統合

各ソリッドには、回転情報を保存するためのフィールドがさらに必要です。追加データを保存する構造の簡単な例を次に示します。

 struct RigidBody { Shape *shape //   Vec2 position Vec2 velocity float acceleration //   float orientation //  float angularVelocity float torque };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

角速度と体の向きの統合は、速度と加速度の統合に非常に似ています。以下に、実行を示す短いコード例を示します（統合の詳細については前のセクションで説明します）。

 const Vec2 gravity( 0, -10.0f ) velocity += force * (1.0f / mass + gravity) * dt angularVelocity += torque * (1.0f / momentOfInertia) * dt position += velocity * dt orient += angularVelocity * dt
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

前に調査した少量の情報があれば、画面上のさまざまなオブジェクトの回転を簡単に開始できます。ほんの数行のコードで、より印象的な何かを構築できます。たとえば、DMを中心に回転しながらフィギュアを空中に投げ、重力がそれを引き下げ、円弧に沿った動きを作成します。

Mat22

上記のように、方向はラジアン単位の単一の値として保存する必要がありますが、多くの場合、一部の図形では小さな回転行列を保存する方が便利です。



これの良い例は、Oriented Bounding Box（OBB）です。 OBBは、ベクトルとして表現できる幅と高さで構成されます。これらの2次元ベクトルは、OBB軸を表す2行2列の回転行列を使用して回転できます。



数学ライブラリにマトリックスクラスを追加することをお勧めしますMat22



。私自身は、オープンソースのデモにある独自の小さな数学ライブラリを使用しています。そのようなオブジェクトがどのように見えるかの例を次に示します。

 struct Mat22 { union { struct { float m00, m01 float m10, m11; }; struct { Vec2 xCol; Vec2 yCol; }; }; };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次の便利な操作があります：角度による作成、列ベクトルによる作成、転置、乗算Vec2



、別の乗算Mat22



、絶対値の計算。



最後の関数により、列x



またはベクターから取得できますy



。列関数は次のように機能します。

 Mat22 m( PI / 2.0f ); Vec2 r = m.ColX( ); //    x
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この手法は、回転軸に沿った単位ベクトルを取得するのに役立ちます：x



またはy



。また、各ベクトルを行に直接挿入できるため、2つの直交単位ベクトルから2行2列の行列を作成できます。この作成方法は、2次元の物理エンジンではあまり一般的ではありませんが、ターンと行列の作業の一般的な理解には役立ちます。



このコンストラクタは次のようになります。

 Mat22::Mat22( const Vec2& x, const Vec2& y ) { m00 = xx; m01 = xy; m01 = yx; m11 = yy; } //  Mat22::Mat22( const Vec2& x, const Vec2& y ) { xCol = x; yCol = y; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

回転行列の最も重要な操作は、角度に基づいて回転を実行することであるため、角度から行列を作成し、ベクトルにこの行列を掛けることが重要です（ベクトルを作成した角度で​​反時計回りに回転させるため）：

 Mat2( real radians ) { real c = std::cos( radians ); real s = std::sin( radians ); m00 = c; m01 = -s; m10 = s; m11 = c; } //   const Vec2 operator*( const Vec2& rhs ) const { return Vec2( m00 * rhs.x + m01 * rhs.y, m10 * rhs.x + m11 * rhs.y ); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

簡潔にするために、反時計回りの回転行列が次の形式である理由を推測しません。

 a = angle cos( a ), -sin( a ) sin( a ), cos( a )
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ただし、少なくともこれが回転行列の形式であることを知っておくことが重要です。回転行列の詳細については、Wikipediaページを参照してください。



その他の関連記事

• 独自の3Dソフトウェアエンジンを作成する、パート2：線形変換

---

ベーシスへの変換

モデル空間と世界の違いを理解することが重要です。モデル空間は、物理的な形式に対してローカルな座標系です。その座標原点はCM内にあり、座標系の方向はFigure自体の軸に合わせられます。



図を世界の空間に変換するには、回転して移動する必要があります。回転は、主に常に原点に対して実行されるため、主に実行されます。オブジェクトはモデル空間（CMの開始点）にあるため、回転はFigureのCMを基準にして実行されます。回転は行列で実行されMat22



ます。サンプルコードでは、方向行列はと呼ばれu



ます。



回転の完了後、ベクトルを追加することにより、オブジェクトをワールド内のその位置に移動できます。



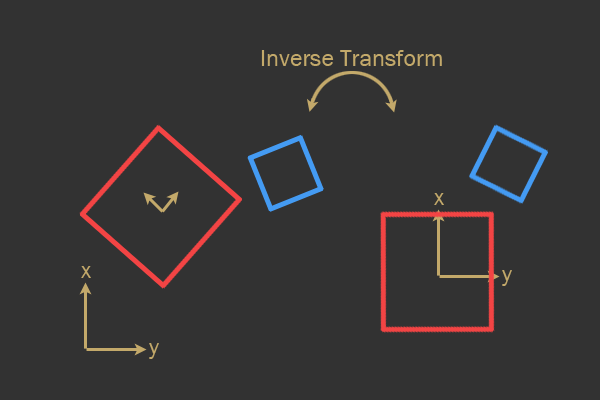
オブジェクトが世界の空間にある場合、逆変換を使用して完全に異なるオブジェクトのモデル空間に移動できます。これを行うには、逆回転と逆運動が実行されます。衝突の認識で単純化されるのは、これらすべての数学的な計算です！









ワールドの空間から赤いポリゴンのモデル空間への逆変換（左から右へ）。



前の画像からわかるように、赤のオブジェクトの逆変換は赤と青の両方のポリゴンに適用されます。つまり、衝突認識テストは、2つの指向形状間の複雑な数学計算を伴うのではなく、AABBおよびOBBチェックのタイプに制限できます。



ほとんどの場合、さまざまな理由でサンプル例のソースコードは常にモデル空間からワールド空間に変換され、モデルに戻ります。衝突検出コードの例を理解するには、これが何を意味するのかを明確に理解する必要があります。

---

衝突認識と多様体生成

このセクションでは、ポリゴンと円の衝突の概要を簡単に説明します。実装の詳細については、ソースコードの例をご覧ください。

ポリゴンとポリゴン

このチュートリアル全体で最も複雑な衝突認識手順から始めましょう。（私の意見では）最も成功した2つのポリゴン間の考え方の衝突チェックはの助けを借りて実施され、分離軸の定理（の分離軸定理、SAT）。



ただし、各ポリゴンの寸法を互いに投影する代わりに、Dirk GregoriusがGDC 2013での講義で説明した、より効果的な新しい方法があります（無料のスライドはこちらです）。



最初に理解することは、参照ポイントの概念です。

基準点

ポリゴンの参照点は、特定の方向で最も遠い頂点です。2つのポイントが特定の方向に同じ距離を持っている場合、いずれかを選択できます。



基準点を計算するには、スカラー積を使用して、特定の方向に沿った符号付きの距離を見つける必要があります。これは非常に単純なので、記事で簡単な例を示します。

 //       Vec2 GetSupport( const Vec2& dir ) { real bestProjection = -FLT_MAX; Vec2 bestVertex; for(uint32 i = 0; i < m_vertexCount; ++i) { Vec2 v = m_vertices[i]; real projection = Dot( v, dir ); if(projection > bestProjection) { bestVertex = v; bestProjection = projection; } } return bestVertex; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

スカラー積は各頂点に使用されます。スカラー積は、指定された方向の符号付きの距離です。つまり、投影距離が最大の頂点が返される頂点になります。エンジンの例では、この操作は特定のポリゴンのモデル空間で実行されます。

分離軸検索

制御点の概念により、2つのポリゴン（ポリゴンAとポリゴンB）間の分離軸を検索できます。この検索の考え方は、ポリゴンAのすべてのエッジをループし、エッジの負の法線でアンカーポイントを見つけることです。











上の画像は、オブジェクトごとに1つずつ、2つの基準点を示しています。青の法線は、青の法線の反対方向に沿った最も遠い頂点として、他のポリゴンのアンカーポイントに対応します。同様に、赤い法線を使用して、赤い矢印の端にあるアンカーポイントを見つけます。



各アンカーポイントから現在のエッジまでの距離は、記号付きの侵入深度になります。最大距離を維持した後、最小貫通軸を記録できます。



以下は、関数を使用して最小の侵入の可能な軸を探すソースコードからの関数の例ですGetSupport



。

 real FindAxisLeastPenetration( uint32 *faceIndex, PolygonShape *A, PolygonShape *B ) { real bestDistance = -FLT_MAX; uint32 bestIndex; for(uint32 i = 0; i < A->m_vertexCount; ++i) { //      A Vec2 n = A->m_normals[i]; //     B  -n Vec2 s = B->GetSupport( -n ); //      A,   //   B Vec2 v = A->m_vertices[i]; //     (   B) real d = Dot( n, s - v ); //    if(d > bestDistance) { bestDistance = d; bestIndex = i; } } *faceIndex = bestIndex; return bestDistance; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この関数は最大の侵入深さを返すため、この深さが正の場合、これは2つの数字が交差しないことを意味します（負の侵入は分割軸がないことを意味します）。



この関数は2回呼び出す必要があり、各呼び出しでオブジェクトAとBを交換します。

インパクトリブとベースリブのクリップ

この段階では、衝突リブとベースリブを決定する価値があり、衝突リブはベースリブの側面に対して切断する必要があります。Erin Catto（Box2Dの作成者とBlizzardが使用するすべての物理学）がこのトピックを詳しく説明した優れたスライドを作成しましたが、これはかなり簡単な操作です。



このクリッピングにより、2つの接点が作成されます。ベースエッジを超えるすべての接点は、接点と見なすことができます。



Erin Cattoのスライドに記載されている内容に加えて、サンプルエンジンにはクリッピング手順の例も含まれています。

多角形の円

円と多角形を衝突させる手順は、多角形と多角形の間の衝突を認識するよりもはるかに簡単です。最初に、前のセクションの制御点を使用するのと同様の方法を使用して、円の中心に最も近いポリゴンのエッジが計算されます：ループでは、ポリゴンの各エッジの法線がバイパスされ、円の中心からエッジまでの距離が検出されます。



円の中心がこの最も近いエッジを超えている場合、連絡先情報を生成できます。その後、手順はすぐに終了します。



最も近いエッジを見つけた後、テストは線分と円のテストに変わります。線分には、ボロノイ領域と呼ばれる3つの興味深い領域があります。図を見てください：









直線セグメントのボロノイ領域。



直感的には、円の中心に応じて、連絡先に関するさまざまな情報を取得できます。円の中心が頂点のいずれかの領域にあると想像してください。これは、円の中心に最も近い点がエッジの頂点になり、頂点から円の中心へのベクトルが衝突の正しい法線になることを意味します。



円がエッジの領域内にある場合、円の中心に最も近いセグメントのポイントは、セグメントへの円の中心の投影になります。コリジョン法線は、エッジの法線になります。



円がどのボロノイ領域にあるかを計算するには、頂点のペア間のスカラー積を使用します。アイデアは、想像上の三角形を作成して、線の上部で作成された角度が90度より大きいか小さいかを確認することです。線分セグメントの各頂点に対して、1つの三角形が作成されます。









エッジの頂点から円の中心へのベクトルをエッジに投影します。



90度より大きい値は、エッジ領域が見つかったことを意味します。エッジの上部の角度が90度を超える三角形がない場合、多様性の情報を生成するには、円の中心をセグメント自体に投影する必要があります。上の図に示すように、エッジの上端から円の中心へのベクトルとエッジベクトル自体のスカラー倍が負の値になる場合、円が存在するボロノイ領域がわかります。



幸いなことに、スカラー積を使用して、符号付きの投影を計算できます。この符号は、角度が90度より大きい場合は負になり、角度が小さい場合は正になります。

---

衝突解決

そして、この瞬間が再び来ました。3回目と最後の時間のために、パルス分解能コードに戻ります。この時までに、摩擦力パルスとともに力パルスを計算する解像度コードの記述をすでに完全に習得しており、線形投影を実行して残りの貫通力を解決することもできます。



摩擦と浸透の解像度に回転成分を追加する必要があります。角速度にエネルギーを追加する必要があります。



摩擦に関する前のパートでそれを残した形式での力のインパルスの解像度は次のとおりです。

$$

$$\: 5: \\ j = \frac{-(1 + e)((V^{A} - V^{B}) * t)}{\frac{1}{mass^{A}} + \frac{1}{mass^{B}}}$$

回転コンポーネントを追加すると、最終的な方程式は次のようになります。

$$

$$\: 6: \\ j = \frac{-(1 + e)((V^{A} - V^{B}) * t)}{\frac{1}{mass^{A}} + \frac{1}{mass^{B}} + \frac{(r^{A} \times t)^{2}}{I^{A}} + \frac{(r^{B} \times t)^{2}}{I^{B}}}$$

上式で $$rは、オブジェクトのCMから接触点までのベクトルのように、再び「半径」です。この式は、Chris HeckerのWebサイトに詳細に表示されます。オブジェクトの特定のポイントの速度は次のとおりであることを理解することが重要です。$r$

$$

$$\: 7: \\ V' = V + \omega \times r$$

回転条件を考慮して、力パルスの適用が少し変更されました。

 void Body::ApplyImpulse( const Vec2& impulse, const Vec2& contactVector ) { velocity += 1.0f / mass * impulse; angularVelocity += 1.0f / inertia * Cross( contactVector, impulse ); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

---

おわりに

これでチュートリアルの最後の部分は終わりです。フォースインパルスの解決、多様体の生成、摩擦、2次元の向きなど、かなり少数のトピックを調べました。



あなたが最後に到達した場合、私はあなたを祝福します！ゲーム用の物理エンジンのプログラミングは、研究が非常に難しい分野です。すべての読者の幸運を祈ります。