🔸 🥤 👨🏽‍🏭 リードソロモンコード。パート2-ガロア体の算術 🙌🏼 🏂🏾 🦒

こんにちは友人！前回、リードソロモンコードが必要なレベルのデータストレージの信頼性を提供する方法について話し始めました。今日は、計算に使用されるガロア体の算術についてもう少し詳しく説明します。

最初に、最後の部分への短い余談。発見-失われたデータを回復できるようにするためには、まず特定の方法で「冗長データ」を生成する必要があります。さらに、数学的な観点から、この問題（コーディング）は、何らかの生成行列を構築し、この行列にソースデータのベクトルを乗算する操作を実行することに限定されます。回復（デコード）手順は、生成マトリックスを逆にし、保存されたデータのベクトルで乗算することで構成されます。概略的に、これは次のように表すことができます。

エンコード手順：

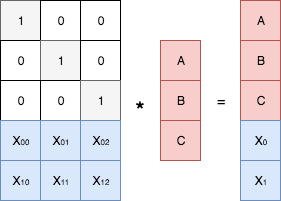
デコード手順：

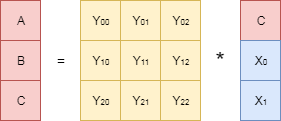
有理数の算術の制限

特定のハードウェアプラットフォームでエンコード/デコード手順を実装する際に遭遇しなければならないいくつかの困難に既に注意しました。そのため、たとえば、コンピューターのメモリ内の数値は通常、固定のバイト数で表されます。その結果、生成行列の要素を乗算すると、ビットのオーバーフローが発生する可能性があります。または、生成行列がその要素として反転されると、任意の精度で保存するのに問題のある有理数が発生する可能性があります。したがって、本日は、上記の問題を回避してこれらの手順を実装する方法について説明します。これについては、前の記事ですでに少し説明したガロア体の理論が役立ちます。

すぐにいくつかコメントをします。まず、この記事は主にエンジニアリングの読者を対象としているため、厳密な数学的定義を避けようとしました。この分野をより正式に紹介したい人にとっては、すぐに関連文献に目を向けることは理にかなっています。私にとっては、アーネスト・ボリソヴィッチ・ヴィンバーグの著書『コースの代数』をお勧めします。第二に、冗長なコーディングアルゴリズムを直接実装するには、有限体の理論の基本的な理解だけで十分です。単純に、乗算、除算、加算、減算、およびすべての計算の一貫したテーブルがこれらのテーブルを使用して実行されると仮定できます。これは、代数のこのセクションを深く掘り下げたくない人にとってのヒントです。

有限集合のフィールドと算術演算

ガロア体の議論に直接進む前に、達成したいことをもう一度繰り返しましょう。行列にベクトルを掛け、行列を反転できるようにしたいのです。そして最も重要なことは、乗算と加算の演算を実行する際にオーバーフローのみを心配せずに整数のみを扱うことです。

また、混乱を避けるために、用語をすぐに扱うことは理にかなっています。まず第一に、一般代数の分野での分野とは何ですか？ウィキペディアが言うように、「 フィールドとは、加算、減算、乗算、除算（ゼロ除算を除く）の操作が定義される要素のセットであり、これらの操作のプロパティは通常の数値演算のプロパティに近い」ガロア体とは何ですか？ ガロア体は、有限数の要素で構成される任意の体です。

G f （ p ）

$Gf（p）$ 、

G f （ p^{n} ）

$Gf（p ^ n）$ -ガロア体の標準的な指定。体の要素の数は括弧で示されています。

現代のコンピューターでは、通常、固定数のビットを使用して数値を格納します。すべてが存在することを計算するのは簡単です

2^{n}

$2 ^ n$ 異なるnビット数、0〜

（ 2^{n} - 1 ）

$（2 ^ n-1）$ 。言い換えると、数の有限セットがあります。このセットで、乗算、除算、加算、減算の演算を決定する一貫した方法でこれから試みます。また、操作の結果も

n

$n$ ビット数！この場合、セットは導入された操作 に関して閉じていると言われます。

有限集合のシステムでの減算操作は、通常、ゼロ要素と反対要素の概念を通じて導入されます。 ゼロ要素

0

$0$ -これは、等式が成り立つような要素です：

a + 0 = a

$a + 0 = a$ どこで

a

$a$ セットの任意の要素です。アイテム

b

$b$ 反対です

a

$a$ 平等が真の場合

a + b = 0

$a + b = 0$ 。通常、反対の要素は

- a

$-a$ 。私たちが望むなら

x

$x$ 引く

y

$y$ 私たちは反対の要素を見つけます

- y

$-y$ そしてそれを積み重ねる

x

$x$ 。したがって、有限集合の任意の要素を減算できるようにするには、この集合の各要素が反対でなければなりません。

状況は除算操作と同様です。ユニットおよび逆エレメントの概念が導入されています。単一要素

1

$1$ 等式が真である要素です

a * 1 = a

$a * 1 = a$ どこで

a

$a$ セットの任意の要素です。アイテム

b

$b$ （によって示される

1 / a

$1 / a$ ）の逆と呼ばれます

a

$a$ もし

a * b = 1

$a * b = 1$ 。減算と同様に、必要に応じて

x

$x$ 非ゼロで除算

y

$y$ 逆要素を見つけなければならない

1 / y

$1 / y$ そしてそれを掛けます

x

$x$ 。任意の要素を分割できるようにするには、セットの各要素（ゼロを除く）が反対でなければなりません。

ガロア体GF（p）の構築

有限の数の集合に対して示された算術演算をどのように決定すれば、集合はそれらに対して閉じられますか？つまり、任意の有限要素セットをガロア体にしたいのです。最初に頭に浮かぶのは、モジュラー演算を使用することです。次に、セットに含まれている場合

p

$p$ 要素、数値の積の結果

a * b

$a * b$ 数になります

（ a * b ） m o d p

$（a * b）mod p$ 。数の合計は次のように定義されます

（ a + b ） m o d p

$（a + b）mod p$ 。

演習として、以下で構成されるセットの加算テーブルと乗算テーブルを作成しましょう。

p = 5

$p = 5$ 要素

\ {0、1、2、3、4 \}

$\ {0、1、2、3、4 \}$ 。

下の2つの表は、セットの各要素の正反対の値を示しています。これらのテーブルを使用して、必要なすべての算術演算を実行できます。やった！

ガロア体の構築 $Gf（p ^ n）$

私たちは成功への正しい道を進んでいるようです。まだ私たちに合わないかもしれない唯一のものは、私たちのフィールドのサイズです-5.ソフトウェアの実装を単純化するために、以下を含むセットで作業することが理にかなっていることは明らかです。

2^{n}

$2 ^ n$ 数字。その後、ニブル、バイト、単語などで操作できます。

一見、違いはセット内の5または256要素であるように思われ、対応するモジュールによる乗算または加算の演算の結果を取得し、完了です。集合の乗算表をもう一度作成してみましょうが、今回は

4 = 2^{2}

$4 = 2 ^ 2$ 要素-

\ {0、1、2、3 \}

$\ {0、1、2、3 \}$ 。起こったことは次のとおりです。

{0,1,2,3}の乗算表

結果の表をよく見ると、そこに重大な欠点があることがわかります。要素2の行に注意してください。この行には単一の要素はありません！これは、反対の要素が存在しないため、他の要素を2で除算できないことを意味します！これは、他の方法で加算テーブルと乗算テーブルを構築する必要があることを意味します。残念ながら、モジュラー演算は機能しなくなりました。

そのため、セットに

4 = 2^{2}

$4 = 2 ^ 2$ オブジェクトの場合、モジュラー演算では一貫した乗算演算を指定できません。実際、どのようなセット、要素の数でも同様の問題が発生します

p

$p$ これは素数ではありません。しかし、他に何が考えられますか？

GFへの加算（p ^ n）

簡単にするために、算術演算を定義するセットには次のものが含まれると仮定します。

2^{n}

$2 ^ n$ 要素。実際、これらは数字です

\ {0、1、2、3、...、2 ^ n-1 \}

$\ {0、1、2、3、...、2 ^ n-1 \}$ 。任意の数

a

$a$ このセットからの分解として表すことができます：

a = a_0 + a_12 ^ 1 + a_22 ^ 2 + ... + a_ {n-1} 2 ^ {n-1}、a_i \ in \ {0,1 \}

$a = a_0 + a_12 ^ 1 + a_22 ^ 2 + ... + a_ {n-1} 2 ^ {n-1}、a_i \ in \ {0,1 \}$

本質的に、これは数値の通常のバイナリ表現です。したがって、セットの任意の数を長さのベクトルと見なすこともできます

n

$n$ その要素はゼロと1です：

a = [a_0、a_1、a_2、...、a_ {n-1}]、a_i \ in \ {0,1 \}

$a = [a_0、a_1、a_2、...、a_ {n-1}]、a_i \ in \ {0,1 \}$

対応するバイナリ分解ベクトルを追加することにより、任意の2つの数値を追加する操作を紹介します。さらに、ベクトルの成分の加算は 2を法として実行されます（一般的な場合、要素の数が

p^{n}

$p ^ n$ モジュロ

p

$p$ ）したがって、結果のベクトルも特定の数のバイナリ表現になり、結果として、セットに属します（セットは加算操作に関して閉じられます）。

a = [a_0、a_1、a_2、...、a_ {n-1}]、a_i \ in \ {0,1 \} \\ b = [b_0、b_1、b_2、...、b_ {n -1}]、b_i \ in \ {0,1 \} \\ c = a + b = [（a_0 + b_0）mod2、...、（a_ {n-1} + b_ {n-1}） mod2]

$a = [a_0、a_1、a_2、...、a_ {n-1}]、a_i \ in \ {0,1 \} \\ b = [b_0、b_1、b_2、...、b_ {n -1}]、b_i \ in \ {0,1 \} \\ c = a + b = [（a_0 + b_0）mod2、...、（a_ {n-1} + b_ {n-1}） mod2]$

導入した加算演算がXORビット演算と同等であることは簡単にわかります。最新のプロセッサはこの操作を非常に迅速に実行できるため、これは非常に優れています。しかし、それだけではありません。明らかに、

a o p l u s a = 0

$a \ oplus a = 0$ 任意の数

a

$a$ 。これは、反対の要素が

a

$a$ 自分自身です

a

$a$ 。だからフィールドで

G f （ 2^{n} ）

$Gf（2 ^ n）$ 加算は減算と同じです！

GFの乗算（p ^ n）

セットに乗算演算を導入することは残っています。これは次のように行われます。しばらくの間、その数を想像してみましょう

a

$a$ 私たちのセットからは、次の形式の多項式です：

a （ x ） = a_{0} + a_{1} x + a_{2} x^{2} + . . . + a_{n - 1} x^{n - 1} 、 a_{i} i n 0, 1

$a（x）= a_0 + a_1x + a_2x ^ 2 + ... + a_ {n-1} x ^ {n-1}、a_i \ in {0,1}$

ここで、多項式の係数は、数のバイナリ展開から取得されます

a

$a$ 。このアプローチでは、たとえば、

100 = 01100100 b

$100 = 01100100b$ 多項式にマッピングされます

x^{6} + x^{5} + x^{2}

$x ^ 6 + x ^ 5 + x ^ 2$ 。

2つの数値の乗算の演算は、指定された数値に対応する多項式の乗算を通じて決定できます。

a \times b = （ a_{0} + a_{1} x + . . . + a_{n - 1} x^{n - 1} ） \times （ b_{0} + b_{1} x + . . . + b_{n - 1} x^{n - 1} ）

$a×b =（a_0 + a_1x + ... + a_ {n-1} x ^ {n-1}）×（b_0 + b_1x + ... + b_ {n-1} x ^ {n-1}）$

さらに、乗算するとき、多項式の係数を使用したすべての演算は2を法として実行されます。

しかし、今、明らかに、別の問題が発生する可能性があります。次数の2つの多項式を乗算する場合

n - 1

$n-1$ 、より高い次数の多項式を取得できますが、これはセット内のどの数値にも対応しません。これは次のように解決されます。次数の既約多項式が選択されます

n

$n$ 。大まかに言えば、これは他の多項式の積として表現できないような多項式であり、記事で詳しく説明しています。その後、列で多項式を除算するアルゴリズムを使用します。これは多くの人がまだ学校のカリキュラムから覚えていることができるので、積の結果を既約多項式に除算します。繰り返しますが、列で除算すると、多項式の係数を使用した演算も2を法として実行されます。その結果、次数以下の多項式が得られます。

n - 1

$n-1$ 、2つの数値の積の結果として取得します。これは、フィールド上で2つの数値の乗算を行う例です

G f （ 2^{8} ）

$Gf（2 ^ 8）$ 既約多項式を使用

x^{8} + x^{4} + x^{3} + x + 1

$x ^ 8 + x ^ 4 + x ^ 3 + x + 1$ 。この多項式は、AES / Rijndael暗号化アルゴリズムで使用されます。

フィールドを調べました

G f （ 2^{n} ）

$Gf（2 ^ n）$ 。カスタムフィールド

G f （ p^{n} ）

$Gf（p ^ n）$ 同様の方法で構築され、数値のバイナリ表現の代わりにのみ使用されます

p

$p$ -1つおよびすべての計算はモジュロで実行されます

p

$p$ 。

任意のサイズの同型写像とガロア体

しかし、別の既約多項式を選択するとどうなりますか？さらに一般的な質問をすることもできます。これらのすべての多項式と列の除算がまったく気に入らないので、他の原則を使用して一貫性のある乗算表を考えた方がいいと思います。これは根本的に新しいものでしょうか？答えはノーです。これらの取得されたフィールドはすべて同型になります。

「数学的」言語から翻訳すると、同型とは、フィールド要素の指定にのみ違いがあり、適切なマッピングルールを選択することで違いを減らすことができることを意味します。

これまでに調査した有限要素セットには2つのタイプがあります。最初のタイプのセットには、ある素数に等しい要素数がありました

p

$p$ 。このようなセットでは、モジュラー演算のみを使用して乗算テーブルと加算テーブルを指定できました。 2番目のタイプには、

p^{n}

$p ^ n$ 、

p

$p$ -シンプル

n > 1

$n> 1$ アイテムの数。このようなセットでは、多項式を使用したスキームを使用して乗算/加算を指定できます。任意のサイズのセット、たとえば6つの要素を含むセットに対して、同様の方法で乗算/加算を設定することは可能ですか？答えはノー、それは不可能です。

実際のところ、有限体はガロア体と呼ばれています。これは、彼が次の重要な特性を発見したためです。

有限体の要素数は常に $p ^ n$ どこで $p$ プライムと $n$ 任意の自然。
すべてのサイズのフィールド $p ^ n$ 同型です。

おわりに

サイクルの2番目の記事は終わりに近づいています。最初の2つの記事では、リードソロモン符号とガロア体に関連する簡単な理論情報を紹介しました。次のパートでは、上記のアルゴリズムのソフトウェア実装の機能についてさらに詳しく説明する予定です。ありがとう

リードソロモンコード。 パート2-ガロア体の算術