車の現在位置を取得し、行きたいパスを見て、このパスにスムーズに曲がり、タクシーを利用します。 それは非常に簡単なことがわかりました。 しかし、都市での移動は、道路のルールに従う必要があるという事実によるものです。
-私の名前はRoma Udovichenkoです。私はミンスクのYandexで、無人車両の方向のトラフィック処理グループの責任者として働いています。 今日は、私たちの仕事の非常に小さいが重要な部分、つまり無人車両の経路構築アルゴリズムについてお話します。
まず、私は車に自分で運転することを教えるために何をする必要があるかを理解したいと思います-センサー、ハングしたカメラ、レーダーなどでそれを掛けました。 私たちはすべてを行うことができますが、仮定のコードを書くことは残っています。
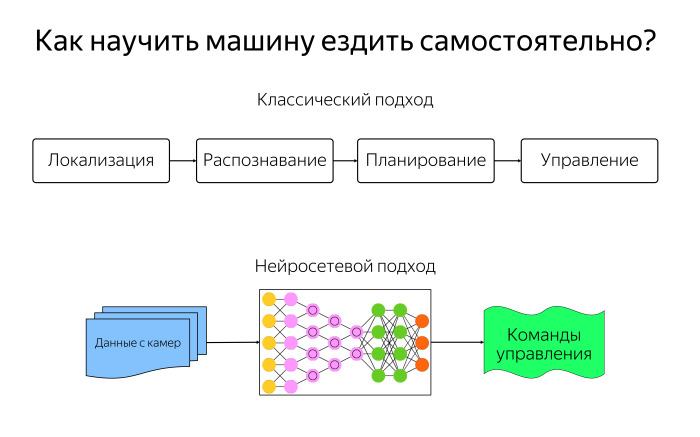
ロボット工学の古典的なアプローチを使用できます。 独立運動のタスクを4つのモジュールに分割します。 ローカリゼーションモジュールは、マシンにその場所を理解させる役割を果たします。 認識モジュール-車の周りにあるもの。 計画モジュールには、周辺の情報があり、どこに行きたいかがわかると、ルートが構築されます。 制御モジュールは、この軌跡をたどるために、到着するためにルートに沿って進む方法を指示します。
しかし、今ではファッショナブルなニューラルネットワークの技術を適用して、何も明示的にプログラムしないと言うことができます。 カメラからの画像をニューラルネットワークに送信します。これは、以前にいくつかの人間の動きについてトレーニングしたものです。 ハンドルを回し、ブレーキをかけ、加速し、大量のデータを取得し、大規模なニューラルネットワークを作成する必要がある状況で、それを学習します。
この方向で多くの作業が行われていますが、実際には、依然として多くのデータが必要であるように思われます。人がさまざまな状況ですべてを正常に繰り返すには、あまりにも多くのニューラルネットワークが必要です。 したがって、今日は古典的なアプローチ、特に経路の計画、進むべき軌道の構築について話します。
経路計画は、1週間では実行できず、次に何か面白いことを続けることが難しい困難なタスクであるのはなぜですか? 車には一般にかなり重要な制限がいくつかあります。 これは、あらゆる方向に転がり、条件付きで即座に停止して減速することができる空間内のボールではありません。 車には現在の方向、車輪の回転角があり、現在の場所の左2メートルに位置することはできません。非常に困難です。 彼はある角度で回ってほぼ前進することができますが、それでも動きは非常に限られています。 そして、私たちが構築している軌道は、運動学から生じる制約を受けます。 たとえば、加速を即座に加速したり、加速を即座に上げることさえできません。

今日は、車が上手く運転できるパスを構築するための、このようなさまざまなアルゴリズムを検討します。 特に、多かれ少なかれ古典的なグラフアルゴリズム、連続的な数学的最適化を使用する最適化方法、ランダムな振る舞いを考慮する確率的アルゴリズム、および非常に特定の問題を解決するが非常によく解決する特殊な方法-一般的な場合よりも優れています。
まず最初に行うことは、グラフアルゴリズムです。 どのアルゴリズムを適用できるかを理解するために最初に答える必要がある質問は、一般的なグラフの作成方法です。 ここに車があります。それがどこにあるかは理解できますが、実際にはグラフはなく、道路上のrib骨の頂点は描かれていません。 どういうわけか、このグラフを自分で作成する必要があります。 最初にできることは、空間全体をセルに分割し、小さなセルを検討し、25 cmから25 cmまたは50 cmから50 cmのセルに分割された地球の表面があると言うことです。次に、隣接するセルをエッジで接続し、それらへのパスを探します。 車が移動できる経路からはかなり離れていますが、ある程度の近似値が得られます。 そして、2次元空間にそのようなピークがあります。
マシンの現在の回転角を追加することで、スペースを複雑にすることができます。 すでにxとyだけでなく、北、南、西、東の方向のマシンの現在の方向もセルになり、何らかの方法で離散化されます。 方向に加えて、マシンの現在の速度、現在の加速度、現在の接線加速度、法線など、多くのことを考慮することができます。 これはすべて考慮することが重要です。 しかし、スペースが複雑になるほど、グラフは複雑になります。
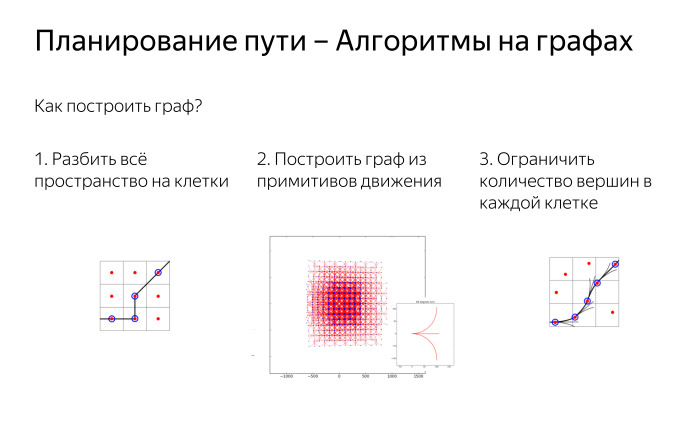
空間をセルに分割することに加えて、プリミティブの形で小さなステップで移動できると言えます。 たとえば、50 cm前進または50 cm前進して左に曲がるか、50 cm前進して右に曲がります。 そして、そのようなプリミティブを使用して、スペース全体をブリッジできます。 明示的なセルはありませんが、これらの小さなステップが互いに適切に調整されている場合、空間を適切にカバーする規則的なグリッドを取得します。
互いにあまりうまく接続されていないプリミティブを考えてみましょう-例えば、左折が89度の角度で発生し、右折が90度の角度で発生したとしましょう。 すると、前の図と同じ数の頂点が既にありますが、それらは十分に結合されておらず、ポイントの密度が非常に高く、遠くのスペースをカバーすることができないため、かなり小さいスペースの領域を占有します。
これらの2つのアプローチを組み合わせて、任意の角度での動きのプリミティブを考慮し、前進、前進、および10度、15度回転することができます。 同時に、とにかくスペースをセルに分割し、1つのセルには1、2、...、k個の頂点しか存在できないと言います。
あるアルゴリズムを使用するプロセスでグラフ内の次の頂点を考慮する場合、セルに新しい頂点があると言い、それに応じて処理します。 後で、別の頂点の指定されたセルに到達したいことが判明した場合、それを考慮しません。 これにより、すべてのピークを使用した場合よりも最適なルートを構築することができなくなります。 ただし、これにより、速度と効率を大幅に向上させることができます。
グラフがあり、それに何らかのアルゴリズムを適用したい。 アルゴリズムA *があります。

ダイクストラのアルゴリズムがあります。これは、A *アルゴリズムよりも少し知られており、グラフのすべての頂点をバイパスして、開始頂点からの距離を増やします。 彼は距離の増加順に優先キューからそれらを取り出します。 上の図では、ピンクの開始頂点が開始点にある場合、開始点から増加する半径にあるすべての頂点を徐々に検討し、最終的には頂点に到達することがわかります。これが目標です。
より効率的に検索するために、開始点からの距離を増やすだけでなく、この距離に最後まで行かなければならない量のヒューリスティックな推定値を追加することでピークを考慮します。 論理は非常に明確です。現在、あるピークに立っていると言っているだけではなく、したがって、開始からある距離で次のピークを順番に検討しています。 また、このパラメーターにいくつかの機能を追加します。これにより、より有望なピークを評価でき、そこからフィニッシュラインに到達する可能性が高いと考えられます。 実際に各ピークからフィニッシュラインに到達するまでの時間はわかりません。知っていれば、道を探す必要がないからです。 しかし、どういうわけかこれを感謝し、下の画像の写真を得ることができます。 どういうわけか目標に向かうピークを評価し、ダイクストラアルゴリズムの場合よりも著しく少ない数のピークを考慮します。 これについて多くのことを話すことができますが、一般的には、アルゴリズムが正しく機能するためには、最終的な頂点までの距離を推定する関数であるヒューリスティックが、実際に移動しなければならない距離を超えないことが必要です。 この場合にのみ、アルゴリズムの正しい動作が保証されます。

ヒューリスティック関数として、さまざまなアプローチを使用できます。 これがA *アルゴリズムの適用の難しさです。 発見できるヒューリスティックが優れているほど、ターゲットに向かってより良くなり、考慮されるピークが少なくなり、より速く動作します。
できる最も簡単なことは、ターゲットまでの距離を直接考慮することです。 明らかに、戦車のようにまっすぐに行くよりも早く最終地点に到着することはできません。
より複雑で効率的なヒューリスティックは、運動学的な制限を考慮しながら、障害を考慮しない距離です。 世界に何も存在せず、私たちだけがターゲットであると仮定しますが、マシンの物理モデルに従って、車は瞬時に左右に移動できず、独自の法則に従って走行します。 障害物がないため、さまざまな場所からターゲットまでの距離を事前に計算し、これをヒューリスティック関数として使用できます。
私たちは反対のことをすることができます:障害物があると言いますが、車はあなたが好きなように前進、後退、左、右に移動でき、素早く加速し、素早くブレーキをかけることができるとしましょう。 障害を考慮して距離を構築します。 繰り返しますが、実際に移動しなければならない距離よりも低い推定値を取得します。
そして最後に、すべてのヒューリスティックのうち、最大値を考慮することができます。 それぞれが実際の距離を超えないため、それらの最大値も実際の距離を超えず、アルゴリズムはうまく機能します。

何が得られますか? アルゴリズムA *を使用すると、障害物を迂回して目標に到達する既知の最適なパスを見つけることができます。 ただし、空間が小さい場合は、x、y、機械の向き、および即座に加速できないという事実のみを考慮します。つまり、これらすべての制限が考慮されます。 グラフに多数のパラメーターを追加すると、非常に高い次元の空間になります。 7次元、8次元、10次元の空間があり、この空間の小さな断片を検討する時間があります。パラメーターの変動性が非常に大きいため、十分に遠いルートを構築することはできません。 状況によっては、A *を使用するのが難しい場合もありますが、どこかで非常によく表示されます。
2番目のオプションは、離散的ではなく、より継続的なアプローチに基づく最適化方法です。


問題のステートメントは次のようになります。時間tに応じて、時間の位置x、yの軌跡を考慮します。つまり、時間tになりたいポイントを理解します。 導関数のアークタンジェントを通る接線の角度を決定できます。この場合、最適な軌道は、機能を最小化するものと言えます。これは、軌道の一部の機能の時間積分です。 ここでの軌道の機能は、何らかの形で急旋回、急加速、障害物に接近するなどの罰金を科します。その後、軌道に沿ってすべての罰金に沿って合計し、標準的な数学で最小化しようとすると一般的には自動車、特に無人車両とはまったく接続されていない装置であれば、何らかの一般的な形で問題を解決します。

罰金の例は何と考えられますか? たとえば、障害物の近くを運転したくない、重みを考慮してこれを考慮したい、速度を自分で決めた希望の速度よりはるかに速くしたり遅くしたくない、と言うことができます。 車を急に床に沈ませて急ブレーキをかけたくないので、二次微分、つまり加速に対してペナルティを科すことができます。
3次導関数を考慮することができます。これはジャークです。つまり、加速度が十分に急激に変化することも望ましくありません。 ちなみに、それは乗車中に揺れる人々の加速度の急激な変化によるものです。 加速が固定され、車が常に加速する場合、研究が示すように、人々は病気になりません。 人間の前庭装置は、それを加速すると速度が低下しますが、常にうまく反応するわけではありません。 急旋回したくないかもしれませんが、角度を制限します。 また、車は物理的にある種の加速よりも速く加速できないという追加の制限があります。 何らかの方法でこれをすべて考慮すると、関数を最小化して結果を得るための抽象的なアルゴリズムを使用して問題を解決できます。
ほとんどの最適化方法では、微分可能で滑らかな滑らかな関数を使用するのが好きなので、距離の計算について個別に話したいと思います。 その後、すべてがうまく機能します。 そして、私たちの車はかなり複雑な形のオブジェクトであり、私たちが回る障害物もalsoな形のオブジェクトです。 したがって、ここではいくつかの単純化が必要です。 たとえば、車は複雑なものではなく、前後に5つだけの円があると言えます。
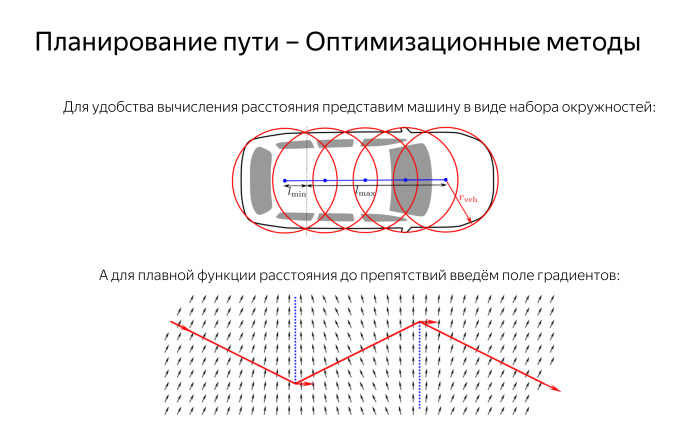
完全ではありませんが、真実に似ていますが、近似は良好です。 また、円を使用すると、あらゆるものまでの距離を非常に簡単に数えることができ、他の幾何学的プリミティブとの交差について円を非常に簡単に確認できます。 中心までの距離が半径よりも短い場合、ここに交差点があります。それ以外の場合はすべて問題ありません。
距離をスムーズに変更するには何が必要ですか? 非凸ポリゴンまでのユークリッド距離には、必要な特性がなく、この非凸が発生する場所では微分が不十分です。 したがって、ポリラインへの勾配フィールドに沿ってこのような擬似距離を構築できます。ここでは赤でマークされ、障害物を表しています。 各ポイントからこのポリラインまでの距離フィールドを簡単に導入できます。このポリラインは、ポリラインに向けられており、必要な微分可能性プロパティを備えています-厳密に最短ではありません。 これをすべて行うと、滑らかで、美しく、きちんとした軌道を構築できます。

そのような方法の利点の中で、良好な軌道と制御空間が継続的に得られるという事実に帰着します。 私たちはそれに乗ることができ、すべての制限はある程度尊重されます。 しかし、残念なことに、ほとんどの最適化手法、またはほとんどすべてが、何らかの形で最適化の試みが行き詰まり、十分な解決策を見つけられないローカルミニマムに苦しんでいます。 数学的微分可能関数の形式ですべてを定式化することは非常に困難であり、これも常に機能するとは限りません。
ただし、解決策があります。 ランダムに機能するアルゴリズムを適用できますが、ある種の近似ルートを迅速かつ便利に構築できます。 たとえば、ツリーであるグラフを繰り返し構築します。 最初は、何もセルに分割せず、プリミティブを構築しません。 車のシミュレーターを使用します。これは一般に、実際の車の動きにできるだけ近い動きをシミュレートすることができます。 そして、出発点を取ります。 その後、空間内のランダムなポイントを繰り返し選択します。 そして-現在構築されているツリーで、それに最も近いノードを見つけます。 この方向への運転のシミュレーションを使用して、このポイントに向かってエッジを構築します。
構築されたツリーからランダムな側に行くたびに、任意の次元の空間でこのツリーの頂点を作成できることがわかります。つまり、各頂点で、マシンの現在の方向、現在の速度、加速度、私たちにとって重要なすべての角度を考慮します。 そして、新しいポイントを取得すると、このポイントに最も近いピークも取得します。 このポイントに向かって5メートルなど、何らかのシミュレーションを実行します。 次に、別のポイントを取り、その方向に渡します。
これにより何が得られますか? 宇宙を探索するたびに、しかし非常に積極的に。 障害物を回避する最適な方法を探していません。 私たちはたださまざまな方向に旅しますが、そのたびに、私たちの空間の最も探検されたセクションからその未知の側面へと移動します。

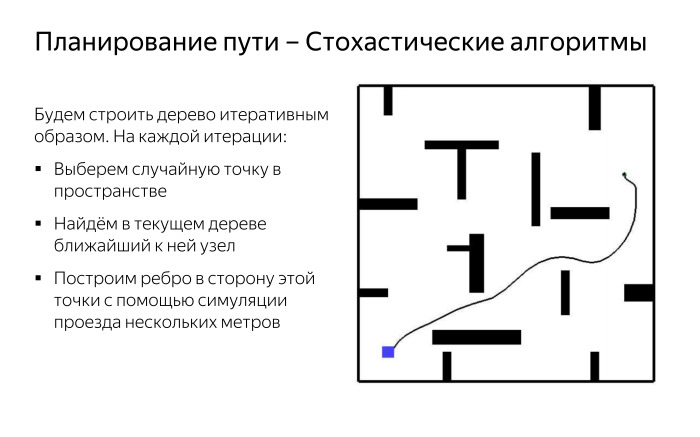
このため、「触手」がさまざまな方向に成長する様子がすぐにわかります。 おそらく最適ではありませんが、かなり高速です。 角の小さな正方形が開始位置です。 そうすれば、目標に到達する方法を見つけることができます。これは、おそらく、まったく最適でエレガントではないように見えますが、かなり迅速に得られます。

結局のところ、多次元空間で非常に迅速に作業できるという利点があります。 正直なシミュレーションを使用してパスを取得するため、ほとんど直接制御ユニットに転送できます。 欠点? ポイントが十分に選択されるという保証はありません。 ソリューションはかなり曲がっており、常に最適とは限りません。
特殊な方法。 車が街を走行するとき、抽象的なポイントAとB、およびランダムな障害物のある非構造化環境はありません。 私たちの街では、すべてが多かれ少なかれ明確です。特定の車線があり、私たちの車の動きは、ほとんど常に車線のほぼ中央を走るという事実にあります。時々、左右に移動して障害物を迂回したり、時には車線を変えて道路の規則に従って曲がります必要な場所に。 あるレーンから別のレーンへの交差点で、私たちは再建しています。

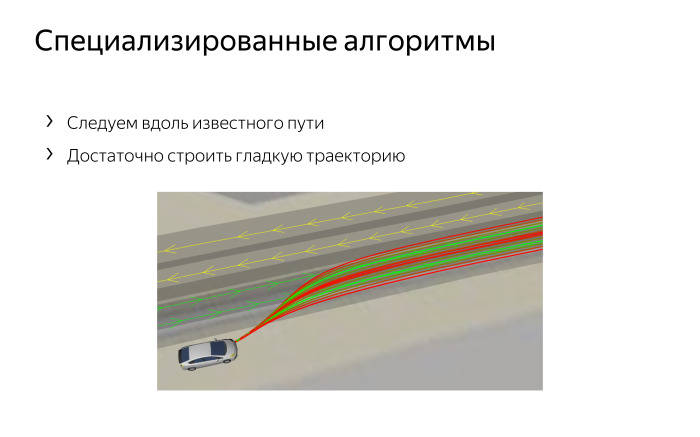
駐車や複雑な操作を行うために、これらのcなツリーが常に必要なわけではありません。 , , - , - -. , . , , , , . . , .

, . , , . , , , , . . , - , , . .
, , . .

, , . , , , . , . . , . , — , , . .

— , . — . . , — . どうもありがとう。