実際にOOPを使用する場合は、 「デザインパターン」などに精通しています。 この標準リストに収まらない便利なパターンがたくさんあることをご存知ですか？ 残念ながら、それらの多くは「関数型プログラミング」に関連付けられており、伝説によると、これは複雑で難解です。 「モノイド」という言葉を10回言うと、悪魔を呼ぶことができます。

Mark Seemanが関数型プログラミングについてすばやく簡単に語っています。 これを行うために、彼はデザインパターンとカテゴリ理論の関係に関する一連の記事を書き始めました。 15分の空き時間があるOOPshnikは、機能だけでなく、適切なオブジェクト指向の設計に関する根本的に新しいアイデアと洞察のセットを手に入れることができます。 決定的な要因は、 すべての例が実際のC＃、F＃、およびHaskellコードであることです。 このhabrapostは、サイクルの最初の部分を翻訳したもので、最初の3つの記事は理解しやすいようにまとめられています。

さらに、2017年11月12〜13日にモスクワのスラビャンスクラディソンで 開催されるDotNext 2017 Moscowカンファレンスに参加して、Markとライブでチャットできます。 マークは「依存性注入から依存性拒否まで」に関する講演を読みます。 チケットはこちらで入手できます 。

エントリー。 モノイド、セミグループ、すべてすべて

このテキストはデザインパターンとカテゴリー理論の間のリンクに関する新しいシリーズの一部です。

関数型プログラミングは通常、その特殊な専門用語で批判されます。 接合体前形態前症などの用語は、初心者に本質を伝えるのに役立ちません。 しかし、石を投げる前に、まず自分のガラスの家を出なければなりません。 オブジェクト指向設計では、 Bridge 、 Visitor 、 SOLID 、 接続性などの名前が使用されます。 言葉はおなじみのように聞こえますが、コードで訪問者パターンを説明または実装したり、「接続性」とは何かを説明したりできますか？

ブリッジという言葉自体は、オブジェクト指向の用語を改善するものではありません。 おそらくそれは彼女をさらに悪化させます。 最終的に、この言葉はあいまいになりました。2つの異なる場所を組み合わせた実際の物理オブジェクトを意味するのでしょうか、それともデザインパターンについて話しているのでしょうか。 もちろん、実際には、コンテキストからこれを理解しますが、これは事実をキャンセルしません-誰かが橋のパターンについて話す場合、事前にそれを学んでいない場合、あなたは全く何も理解しません。 単語がおなじみのように聞こえるからといって、それが便利になるわけではありません。

多くのオブジェクト指向プログラマーは、「引数として受け取ったものと同じ型を返す操作」の有用性を発見しました。 それにもかかわらず、そのような記述、そのような辞書は非常に不便です。 この操作を一言で説明する方が良いと思いませんか？ モノイドですか、 セミグループですか？

オブジェクト指向の洞察

ドメイン駆動設計の本で、 Eric EvansはClosure of Operationsの概念について語っています。 名前が示すように、これは「戻り値の型が引数の型と一致する操作」です。 C＃では、署名public Foo Bar(Foo f1, Foo f2)



持つメソッドである可能性があります。 このメソッドは、2つのFoo



オブジェクトを入力として受け取り、 Foo



オブジェクトも返します。

エヴァンスが指摘したように、このように設計されたオブジェクトは、まるで算術を形成しているように見え始めます。 Foo



を受け入れてFoo



を返す操作がある場合、それは何でしょうか？ たぶん追加？ 乗算？ 他の数学演算はありますか？

一部のエンタープライズ開発者は、単に「ビジネスをして先に進みたい」だけで、数学にまったく悩まされていません。 彼らにとって、コードをより「数学的な」ものにするという考えは非常に物議をかもします。 それにもかかわらず、「数学が好きではない」場合でも、加算、乗算などの意味を確実に理解できます。 すべてのプログラマーが理解しているように、算術は強力な隠phorです。

彼の有名な本「 Test-Driven Development：Example by」では、 Kent Beckは同じ考えを利用したようです。 私は彼がどこかでこれについて直接書いたとは思わないが。

エヴァンスが書いたのは、モノイド、セミグループ、および抽象代数からの同様の概念です。 公平を期して、最近彼と話をしましたが、今では彼はこれらすべてに精通しています。 彼はDDDが書かれた2003年にそれらを理解しましたか-私は知りませんが、私は間違いなく理解しません。 ここでの私の仕事は、指を突くのではなく、非常に賢い人々がOOPで使用できる原則を開発したことを示すことです。

これはすべてどうやってつながっているの

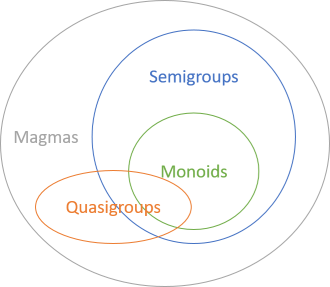
モノイドとセミグループは、マグマと呼ばれるより大きな操作グループに属します。 これについては後で説明しますが、モノイドから始めてセミグループに進み、マグマに移ります。 すべてのモノイドはセミグループであり、その逆は当てはまりません。 つまり、モノイドはセミグループのサブセットを形成します。

これらは、2つのFoo



値を入力として受け取り、出力でFoo



型の値を返す操作の形式でバイナリ操作を記述します。 両方のカテゴリは（直観的な）法律で記述されています。 違いは、モノイドの法則がセミグループの法則よりも厳密であることです。 用語に固執しないでください。「法」という言葉は、深刻な複雑な数学が関係しているように聞こえるかもしれませんが、これらの「法」はシンプルで直感的です。 それらについては、次の部分で説明します（そのうち約15個）。

それらはすべて数学と密接に関連しているという事実にもかかわらず、とりわけ、優れたオブジェクト指向設計のための多くのアイデアを提供するように設計されています。

まとめ

通常のオブジェクト指向プログラマーの場合、 モノイドやセミグループのような用語は、建築の宇宙飛行士が住む数学、アカデミー、象牙の塔のような匂いがします。 しかし、実際には、これらはシンプルで便利なアイデアであり、誰もが誰がこれに15分を費やすのが面倒ではないかを理解できます。

パート1.モノイド

結論：OOPプログラマーのためのモノイドの紹介。

このセクションは、モノイド、セミグループ、および関連する概念に関する一連の記事の一部です。 このセクションを学習すると、モノイドとは何か、セミグループとはどのように異なるかを理解できます。

モノイドは、セミグループのサブセットを形成します。 モノイドが機能するルールは、セミグループよりも厳密です。 最初にセミグループに対処し、それらに基づいてモノイドに進む方がよいと判断することもできます。 厳密に言えば、階層の観点では、これは理にかなっています。 しかし、モノイドははるかに直感的だと思います。 モノイドの最初の例を見ると、それらが日常生活からのものを記述していることがすぐにわかります。 モノイドの例を見つけるのは簡単ですが、セミグループの良い例を選択するには、試してみる必要があります。 したがって、モノイドから始めます。

モノイド法

加算（ 40 + 2



）と乗算（ 6 * 7



）の共通点は何ですか？

これらの操作の両方

• 連想
• 二項演算です
• 中立的な要素を持っている

モノイドを形成するために必要なのはこれだけです。 中立的な要素の結合性と存在は、「モノイド法」または「モノイド法」（英語ではモノイド法 ）と呼ばれます。 モノイドはデータ型と操作の組み合わせであることは注目に値します。 つまり、単なる型ではなく、この型で機能する関数（またはメソッド）です。 たとえば、加算と乗算は、数値に作用する2つの異なるモノイドです。

バイナリ

最も単純なものから始めましょう。 2つの値で機能する場合、操作は「バイナリ」です。 おそらく、「バイナリ」という言葉に言及すると、主に101010などのバイナリデータが表示されますが、この単語はラテン語に由来し、「アリティ2」に関連するものを意味します。 天文学者は時々バイナリスターについても話しますが、現在ではこの言葉は主にコンピュータの文脈で使用されています。バイナリデータに加えて、おそらくバイナリツリーについて聞いたことがあるでしょう。 二項演算といえば、両方の入力値が同じ型であり、戻り値の型も入力型と一致することを意味します。 言い換えれば、C＃では、このようなメソッドは有効なバイナリ演算です。

 public static Foo Op(Foo x, Foo y)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Op



がFoo



クラスのインスタンスメソッドである場合、次のようになります。

 public Foo Op (Foo foo)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

一方、これはもはやバイナリ操作ではありません。

 public static Baz Op(Foo f, Bar b)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

2つの入力引数を取りますが、型は異なり、戻り値の型も異なります。

すべての引数と戻り値は同じ型であるため、バイナリ操作はEric EvansがDomain-Driven Designの Closure of Operationsと呼んだものです。

連想性

モノイドの形成のために、二項演算は必ず連想的でなければなりません。 これは単に、計算の順序が重要でないことを意味します。 たとえば、追加の場合、これは次のことを意味します。

 (2 + 3) + 4 = 2 + (3 + 4) = 2 + 3 + 4 = 9
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

乗算についても同様：

 (2 * 3) * 4 = 2 * (3 * 4) = 2 * 3 * 4 = 24
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

上記のOp



メソッドについて説明する場合、結合性では、次のコードに対してareEqual



がtrue



である必要があります。

 var areEqual = foo1.Op(foo2).Op(foo3) == foo1.Op(foo2.Op(foo3));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

左側では、 foo1.Op(foo2)



計算され、次に結果がfoo3



に適用されfoo3



。 右側では、 foo2.Op(foo3)



最初に計算され、結果はfoo1.Op



引数にfoo1.Op



左側と右側は==演算子を使用して比較されるため、結合性ではareEqual



がtrue



必要がありtrue



。

この構造全体がC＃で機能するためには、何らかの自作モノイドFoo



場合、 Equals



をオーバーロードし、 ==



演算子を実装する必要があります。

中立要素

モノイドの3番目のルールは、中立的な要素が存在する必要があるということです。 通常、 ユニットと呼ばれます（最適な名前ではありませんが、かさばる「中立要素」よりも優れています）。 将来的にはそれを呼び出します。

単位は、「何もしない」値です。 たとえば、追加の場合は0



です0



ゼロを追加しても元の値とは何も変わらないため、変更されません。

 0 + 42 = 42 + 0 = 42
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

簡単な演習：乗算の単位を推測します。

上記の合計の記録は、ユニットが左側で使用される場合と右側で使用される場合の両方で、ユニットが中立的に動作する必要があることを意味します。 Foo



オブジェクトの場合、これは次のように記述できます。

 var hasIdentity = Foo.Identity.Op(foo) == foo.Op(Foo.Identity) && foo.Op(Foo.Identity) == foo;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ブール値を処理するモノイドがいくつかあります： allとanyです。 あなたはどう思いますか、彼らはどのように機能しますか？ 彼らのユニットは何ですか？

演習として、 any



（およびそれらをグーグルで）を振り返ることができます。 次のセクションでは、他のより興味深いモノイドを示します。 このハブポストでは、行、リスト、およびシーケンスのみが考慮されます-残りの記事はまだ執筆中です。

実際、「数値のように振る舞う」データ型がある場合、ほとんどの場合、それからモノイドを作成できます。 加算は最も簡単な候補の1つです。なぜなら、最も簡単に理解でき、測定単位のようなものをいじる必要がないからです。 たとえば、.NET基本クラスライブラリには、 Addメソッドを持つTimeSpan構造があります。 演算子==



彼女も持っています。 一方、 TimeSpan



にはMultiply



メソッドがありません。なぜなら、2つの期間を乗算した結果はどうなるのでしょうか？ スクエアタイム ？

まとめ

モノイド（モナドと混同しないでください）は、モノイドの2つの法則を満たす2項演算です。演算は連想的であり、中立要素（ユニット）が存在する必要があります。 モノイドの主な例は加算と乗算ですが、他にもたくさんあります。

（ちなみに、乗算の単位は単位（1）で、 all



がブール値and



であり、 any



もブール値or



です。）

パート2.行、リスト、シーケンスのモノイド

一番下の行：文字列、リスト、およびシーケンスは、本質的に同じモノイドです。

このセクションはモノイドに関する一連の記事の一部です。

要するに、 モノイドは、中立要素（ ユニット 、または英語の用語ではidentityと呼ばれる）を持つ連想バイナリ操作です。

シーケンス

C＃では、値の遅延シーケンスはIEnumerable<T>



を使用してモデル化されます。 シーケンスのペアを組み合わせるには、一方を他方に追加します。

 xs.Concat(ys)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、 xs



とys



はIEnumerable<T>



インスタンスです。 Concat拡張メソッドはシーケンスを結合します。 次のシグネチャがあります： IEnumerable<T> Concat<T>(IEnumerable<T>, IEnumerable<T>)



、したがって、バイナリ操作です。 連想性があり、ユニットを持っていることがわかった場合、モノイドであることを証明します。

計算のシーケンスは結果を変更しないため、シーケンスは結合的です。 結合性はモノイドプロパティであるため、それを実証する1つの方法は、 プロパティベースのテストを使用することです。

 [Property(QuietOnSuccess = true)] public void ConcatIsAssociative(int[] xs, int[] ys, int[] zs) { Assert.Equal( xs.Concat(ys).Concat(zs), xs.Concat(ys.Concat(zs))); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この自動テストではFsCheckを使用します （はい、C＃でも動作します！） Concat



結合性を実証します。 問題を簡素化するために、 xs



、 ys



およびzs



配列として宣言されています 。 FsCheckは配列の作成方法をネイティブに知っているため、これが必要ですが、 IEnumerable<T>



は組み込みのサポートがありません。 もちろん、FsCheck APIを使用して自分でiEnumerable<T>



作成することもできますが、これは例を複雑にし、新しいものを追加しません。 結合性プロパティは、 IEnumerable<T>



他の純粋な実装にも適用されます。 私を信じないなら、試してみてください。

Operation Concat



にはユニットがあります。 ユニットは、次のテストで確認された空のシーケンスです。

 [Property(QuietOnSuccess = true)] public void ConcatHasIdentity(int[] xs) { Assert.Equal( Enumerable.Empty<int>().Concat(xs), xs.Concat(Enumerable.Empty<int>())); Assert.Equal( xs, xs.Concat(Enumerable.Empty<int>())); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

つまり、空のシーケンスがシーケンスの先頭または末尾に接着されている場合、元のシーケンスは変更されません。

Concat



はユニットを持つ連想バイナリ操作であるため、モノイドです。 証明されています。 ◼

リンクリストとその他のコレクション

FsCheckを使用した上記のテストは、 Concat



が配列のモノイドであることを示しました。 このプロパティは、すべての純粋なIEnumerable<T>



実装に対して保持されます。

Haskellでは、遅延シーケンスはリンクリストとしてモデル化されます。 Haskellのすべての式がデフォルトの式であるという理由だけで、それらは怠areです。 モノイドの法則は、Haskellのリストにも有効です。

 λ> ([1,2,3] ++ [4,5,6]) ++ [7,8,9] [1,2,3,4,5,6,7,8,9] λ> [1,2,3] ++ ([4,5,6] ++ [7,8,9]) [1,2,3,4,5,6,7,8,9] λ> [] ++ [1,2,3] [1,2,3] λ> [1,2,3] ++ [] [1,2,3]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Haskellでは、 ++



演算子はC＃のConcat



とほぼ同じですが、この操作は連結ではなくappendと呼ばれます 。

F＃では、F＃のすべての式がデフォルトの式であるため、リンクリストは積極的に（遅延ではなく）初期化されます。 ただし、モノイドのすべてのプロパティがまだ満たされているため、リストはモノイドのままです。

 > ([1; 2; 3] @ [4; 5; 6]) @ [7; 8; 9];; val it : int list = [1; 2; 3; 4; 5; 6; 7; 8; 9] > [1; 2; 3] @ ([4; 5; 6] @ [7; 8; 9]);; val it : int list = [1; 2; 3; 4; 5; 6; 7; 8; 9] > [] @ [1; 2; 3];; val it : int list = [1; 2; 3] > [1; 2; 3] @ [];; val it : int list = [1; 2; 3]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

F＃では、連結演算子は++



ではなく@



++



が、その動作はHaskellの場合とまったく同じです。 ◼

行

ほとんどのプログラミング言語でテキスト値がstring



と呼ばれる理由を疑問に思ったことはありませんか？ 結局のところ、英語の文字列はロープであり 、繊維で作られたそのような長い柔軟なものです。

プログラミングでは、通常、テキストはメモリ内で文字の連続したブロックとして表されます。 通常、プログラムは、行の終わりの兆候である何かに達するまで、このような連続したメモリブロックを読み取ります。 したがって、文字列は順序付けられます。 シーケンスまたはリストのように見えます。

実際、Haskellでは、 String



型は扱いにくいものではなく、 [Char]



同義語です（これは、 Char



値のリストです）。 したがって、他のタイプのリストでできることはすべて、 String



でもできます。

 λ> "foo" ++ [] "foo" λ> [] ++ "foo" "foo" λ> ("foo" ++ "bar") ++ "baz" "foobarbaz" λ> "foo" ++ ("bar" ++ "baz") "foobarbaz"
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

明らかに、 String



++



はHaskellのモノイドです。

同様に、.NETでは、 System.String



はIEnumerable<char>



実装します。 類推により、我々はそれらがモノイドであることが判明すると推測することができます-そしてこれはほとんど事実です。 見てみましょう、それらは正確に連想的です：

 [Property(QuietOnSuccess = true)] public void PlusIsAssociative(string x, string y, string z) { Assert.Equal( (x + y) + z, x + (y + z)); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

C＃では、 +



演算子がstring



に対して実際に定義されており、このFsCheckのテストからわかるように、これは結合性です。 そして、彼はほとんどユニットを持っています。 文字列の世界で空のリストに相当するものは何ですか？ もちろん、空の行：

 [Property(QuietOnSuccess = true)] public void PlusHasIdentity(NonNull<string> x) { Assert.Equal("" + x.Get, x.Get + ""); Assert.Equal(x.Get, x.Get + ""); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

null



必要ないことを手動でFsCheckに説明する必要がありました。 いつものように、 null



はコードの議論の際に棒を車輪に入れます。

ここでの問題は、 "" + null



およびnull + ""



が同じ値- ""



返し、入力値（ null



）と等しくないことです。 つまり、この特殊なケースが存在するため、 ""



+



演算子の実際の単位で""



ません。 （そして、ちなみに、 null



null + null



は... ""



返すため、 null



も単位でnull



ありません！もちろん、それだけを返します...）。 ただし、これは実装の機能です。 練習として、 null



を持っているにもかかわらず、 string



有効なモノイドにするC＃のメソッド（拡張）を考えてみてください。 思いつくとすぐに、Haskellと同じように、文字列の連結が.NETのモノイドであることをすぐに示します。 ◼

無料モノ​​イド

以前の記事で、数字の加算と乗算がモノイドであることを示したことを思い出してください。 少なくとも1つ以上の数のモノイドがあり、これはシーケンスです。 ジェネリックシーケンス（ IEnumerable<T>



）が存在する場合、番号を含むすべてを含めることができます。

3



と4



2つの数値があり、それらを結合したいと考えていますが、それらをどのように正確に結合するかはまだ明確ではありません。 ソリューションを延期するために、両方の数値を単一の配列に入れることができます（英語ではこれはシングルトン配列と呼ばれます-1つの要素を持つ配列で、これはシングルトンパターンとは関係ありません）。

 var three = new[] { 3 }; var four = new[] { 4 };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

以前に証明したように、シーケンスはモノイドであるため、安全に組み合わせることができます。

 var combination = three.Concat(four);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結果は、両方の数値を含むシーケンスです。 現時点では情報を失っていないため、これらの数値を組み合わせる方法が明確になり次第、以前に収集したデータを計算するだけで済みます。 これは無料モノ​​イドと呼ばれます。

たとえば、数値の合計を取得する必要があると判断しました。

 var sum = combination.Aggregate(0, (x, y) => x + y);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

（はい、 Sumメソッドがあることは承知していますが、現在の目標は詳細を把握することです）。 このAggregateは、最初の引数としてseed



値を取り、2番目として組み合わせ関数を取ります。

そして、あなたは製品を手に入れることができます：

 var product = combination.Aggregate(1, (x, y) => x * y);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

どちらの場合も、 seed



値は対応するモノイド演算の1であることに注意してください0



は加算、 1



は乗算です。 同様に、集計関数は、対応するモノイドを参照するバイナリ演算を使用します。

興味深いことに、これは「無料モナド 」に似た「無料モノイド」と呼ばれます。 どちらの場合でも、すべてのデータを収集してすぐに解釈することはできません。その後、事前に準備された多くの「計算機」のいずれかにこのデータをロードします。

まとめ

.NETのシーケンスや配列、F＃やHaskellのリストなど、多くのタイプのコレクションは、連結に対するモノイドです。 Haskellでは、文字列はリストであるため、文字列の連結は自動的にモノイドになります。 .NETでは、文字列の+



演算子はモノイドですが、 null



が存在しないふりをした場合のみです。 ただし、それらはすべて同じモノイドのバリエーションです。

前のパートで示したように、追加はすべてのモノイドの中で最も直感的で「自然」であるため、C＃が+



を使用して文字列を連結するのは良いことです。 あなたは学校の算数を知っているので、追加の比phorをすぐに理解できます。 しかし、モノイドは比phor以上のものです。 これは特別なバイナリ演算を説明する抽象概念であり、その1つ（それが起こった）は加算です。 これは概念の一般化であり 、これはすでに知っている抽象化です。

おわりに

これでこの記事は終わりです。 バックリンクでリンクされたHabréへの連続した投稿という形で、オリジナルと同じ方法で公開される情報がまだたくさんあります。 以下：記事のオリジナルは©Mark Seemann 2016、翻訳はJUG.ru Groupが、翻訳者はOleg Chirukhinです。

2017年 11月12〜13日にモスクワのスラビャンスカヤラディソンで開催されるDotNext 2017モスクワ会議にアクセスして、著者とライブでチャットできます。 マークは「依存性注入から依存性拒否まで」に関する講演を読みます。 チケットはこちらで入手できます 。