サンプルサイズの決定方法

統計はすべてを知っています。 IlfとE. Petrov、「12の椅子」

大きなショッピングセンターを建設していて、駐車場への入り口の交通量を評価したいとします。 いいえ、別の例を挙げましょう...彼らはとにかくこれを決してしません。 ポータル訪問者の嗜好を評価する必要があります。そのためには、ポータル訪問者間でアンケートを実施する必要があります。 データ量と考えられるエラーを相関させる方法は？ 複雑なことはありません-サンプルが大きくなればなるほど、エラーは小さくなります。 ただし、ここには微妙な違いがあります。

理論的最小値

メモリを更新する必要はありません。これらの用語はさらに役立ちます。

• 人口 -研究が行われているすべてのオブジェクトのセット。
• サンプル -サブセット、調査に直接関与する母集団全体のオブジェクトの一部。
• 第一種の間違い -（α）帰無仮説を否定する確率。
• 第2種の間違い -（β）帰無仮説を否定しない確率、それは偽です。
• 1-β-基準の統計的検出力。
• μ0およびμ1-帰無仮説および対立仮説の平均値。

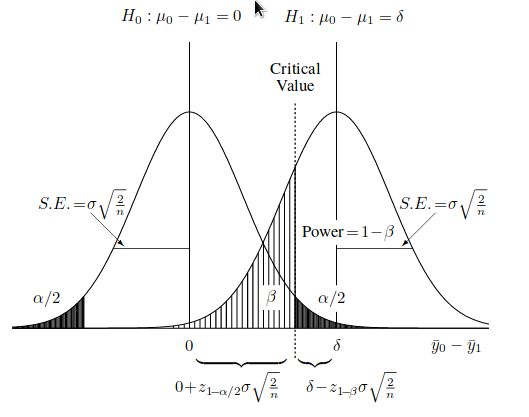
すでに定義自体に、第1種と第2種のエラーには議論と解釈の余地があります。 それらをどのように決定し、どれをゼロとして選択するのですか？ 土壌または水質汚染のレベルを調べる場合、帰無仮説をどのように定式化しますか：汚染があるか、汚染がないか？ しかし、オブジェクトの一般的な母集団からのサンプルサイズはこれに依存します。

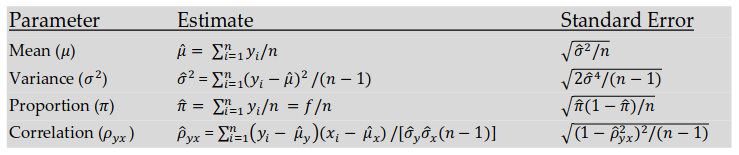
サンプルと同様に初期母集団は任意の分布を持つことができますが、 正規分布またはガウス分布は 中心極限定理による平均値です。

特に分布パラメーターと平均値に関して、いくつかのタイプの推論が可能です。 これらの最初のものは信頼区間と呼ばれます 。 指定された信頼係数を使用して、可能なパラメーター値の間隔を示します。 したがって、たとえば、 μの 100(1-α)%



信頼区間はこのようになります（Lv。1）。

$$

$$\ hat {\ mu} \ pm t _ {{\ alpha / 2}; df} \ sqrt {\ frac {\ hat \ sigma ^ 2} {n}}$$

• df-英語の「自由度」からの自由度= n-1。
• $$$t _ {{\ alpha / 2}; df}$ -両側臨界値、 t-
  
  
  
  。

2番目の推論は仮説検定です。 それはこのようなものかもしれません。

• H ₀ ：μ= h
• H ₁ ：μ> h
• H ₂ ：μ<h

μの 信頼区間が 100(1-α)



場合、H ₁およびH _2を選択できます。

• 信頼区間の下限が 100(1-α) < h
  
  
  
  場合、H ₂を優先してH ₀を拒否します。
• 信頼区間の上限が 100(1-α)
  
  
  
  > hの場合、 H ₀を拒否してH ₁を優先します。
• 信頼区間 100(1-α)
  
  
  
  にhが含まれる場合、H ₀を拒否することはできず、 この結果はundefinedと見なされます。

全母集団から1つのサンプルのμの値を確認する必要がある場合、基準は次の形式になります。

• H ₀を破棄し、H ₁を受け入れる：μ> h $$$t> t _ {{\ alpha / 2}; df}$ 。
• H ₀を破棄し、H ₂を受け入れます。μ<hの場合 $$$t <t _ {{\ alpha / 2}; df}$ 。
• H ₀を拒否することは不可能です $$$| t | <t _ {{\ alpha / 2}; df}$ 。

どこで $$$t =（\ hat {\ mu}-h）/ \ sqrt \ frac {\ hat \ sigma ^ 2} {n}$ 。

信頼区間、精度、およびサンプルサイズ

最初の方程式を取り、そこから信頼区間の幅を表します （Lv。2）。

$$

$$w = 2t _ {{\ alpha / 2}; df} \ sqrt {\ frac {\ hat \ sigma ^ 2} {n}}$$

場合によっては、 t-



をz



置き換えることができます。 別の単純化は、 wの半分を測定誤差Eで置き換えることです。その後、式は次の形式になります（Lv。3）。

$$

$$E = z _ {\ alpha / 2} \ sqrt {\ frac {\ hat \ sigma ^ 2} {n}}$$

ご覧のとおり、入力データの量が増えると 、 エラーは本当に減少します 。 求められているものを推測するのは簡単です（Lv。4）。

$$

$$n = \左[\ frac {z _ {\ alpha / 2} * \ sigma} {E} \右] ^ 2$$

練習-Rでカウントする

トラップ内の昆虫数のこのサンプルの平均値が1であるという仮説を検証しましょう。

• H ₀ ：μ= 1
• H ₁ ：μ> 1

虫	0	1	2	3	4	5	6
T	10	9	5	5	1	2	1

 > x <- read.table("/tmp/tcounts.txt") > y = unlist(x, use.names="false") > mean(z);sd(z) [1] 1.636364 [1] 1.654883
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

平均と標準偏差はほぼ等しいことに注意してください。これはポアソン分布にとって自然なことです。 t-



およびdf=32



95％信頼区間。

 > qt(.975, 32) [1] 2.036933
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最後に、平均値1.05-2.22のクリティカルインターバルを取得します。

 > μ=mean(z) > st = qt(.975, 32) > μ + st * sd(z)/sqrt(33) [1] 2.223159 > μ - st * sd(z)/sqrt(33) [1] 1.049568
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

その結果、95％の確率でμ > 1であるため、H ₀を拒否し、H ₁を取得する必要があります。

同じ例で、ランダムサンプルを使用して得られた推定値ではなく、実際の標準偏差-σを知っていると仮定すると、特定の誤差に必要なn



を計算できます。 E=0.5



カウント。

 > za2 = qnorm(.975) > (za2*sd(z)/.5)^2 [1] 42.08144
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

風補正

実際、 μ （平均）はまだ推定されていませんが、 σ （分散）を知っていると信じる理由はありません。 このため、式4は、組み合わせ論の分野からの特に洗練された例を除き、ほとんど実用的ではありません。また、 n



の現実的な方程式n



、未知のσで多少複雑です（Lv。5）。

$$

$$n = 4 \チルダ\ sigma ^ 2（z _ {\ alpha / 2} / w）^ 2 + z ^ 2 _ {\ alpha / 2} / 2$$

最後の式のσにはヘッダー（^）ではなく、チルダ（〜）が付いていることに注意してください。 これは、最初はランダムサンプルの推定標準偏差さえも持っていないという事実の結果です。 $$$\帽子\シグマ$ 、代わりに計画を使用します- $$$\チルダ\ sigma$ 。 最後はどこで入手できますか？ 専門家による評価、大まかな見積もり、過去の経験など、天井からそれを言うことができます。

そして、5番目の方程式の右側の2番目の項はどうでしたか？ 以来 $$$z _ {\ alpha / 2} <t _ {{\ alpha / 2}; df}$ ガンターの修正が必要です。

式4と5に加えて、さらにいくつかの近似式がありますが、これはすでに別の投稿に値します。

使用材料

1. サンプルサイズ
2. 仮説検定