⌚️ 🌦️ 🔗 最近傍検索方法 🤳🏾 🛀🏾 🍘

データサイエンスの分野のプログラマや専門家は、よく似たユーザープロファイルを見つけるか、似たような音楽を選択するという課題に直面することがよくあります。ソリューションは、オブジェクトをベクトル形式に変換し、最も近いものを見つけることに還元できます。

また、顔認識問題で最近傍を検索する必要性に直面しました。そこで、ニューラルネットワークを使用して顔のベクトル表現を形成し、すでに有名な人々の最も近いベクトルを探します。最初に、検索のために、Spotifyを含むよく知られた実績のあるアルゴリズムとしてAnnoyを選択しました。しかし、彼らはすぐに、彼の記憶欲求で、私たちはRAMに適合しなかったか、多くの精度を失ったことに気付きました。これは少し研究につながりました。その結果を以下で説明します。

理論を実践で薄めるために、この記事には、単語に最も近いものを探す小さなコードがあります。人気のあるword2vecを使用してベクター表現を取得します。このアルゴリズムは、意味的に類似した単語に対して近いベクトルを生成します。 word2vec CBOWでは、環境によって単語を予測する小さなニューラルネットワークの学習の副産物としてベクトル表現が取得されます。ベクトルを使用すると、king +（woman-man）= queenのような算術演算ができるのは興味深いです。

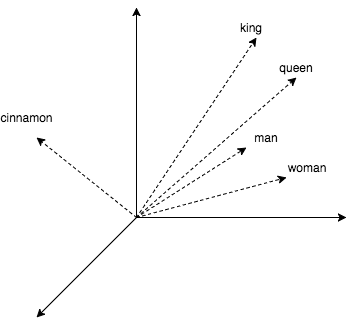
単語の埋め込み

コードでこれを操作する方法を見てみましょう。

model = gensim.models.KeyedVectors.load_word2vec_format('./GoogleNews-vectors-negative300.bin', binary=True) start = time.time() pprint.pprint(model.wv.most_similar(positive=['king'])) print('time:', time.time() - start) print('king + (woman - man) = ', model.wv.most_similar(positive=['woman', 'king'], negative=['man'])[0]) print('Japan + (Moscow - Russia) = ', model.wv.most_similar(positive=['Moscow', 'Japan'], negative=['Russia'])[0])

取得するもの：

  [(u'kings', 0.7138045430183411), (u'queen', 0.6510956883430481), (u'monarch', 0.6413194537162781), (u'crown_prince', 0.6204219460487366), (u'prince', 0.6159993410110474), (u'sultan', 0.5864823460578918), (u'ruler', 0.5797567367553711), (u'princes', 0.5646552443504333), (u'Prince_Paras', 0.5432944297790527), (u'throne', 0.5422105193138123)] time: 0.236690998077 king + (woman - man) = (u'queen', 0.7118192911148071) Japan + (Moscow - Russia) = (u'Tokyo', 0.8696038722991943)

上記の例では、ライブラリを使用してgensimテキストと、Googleのword2vec モデル（1.5 GB）を処理しました。このモデルには、300万の単語と短いフレーズがあります。コード出力は、女王、君主、王子が王に近いことを示しています。また、ベクトルを使用した演算が機能することを確認しました。ただし、リクエストごとに1/4秒はあまり魅力的ではなく、結局のところ、gensimはブルートフォース検索の比較的良い実装を持っています（すべての既知のオブジェクトまでの距離の計算を使用）。次に、精度のわずかな損失のみで、この時間を数百分の1に短縮できる方法を検討します。

しかし、単純なアイデアから始めましょう：平面で2つの半分に分割することにより、探索空間を狭めるようにしてください。また、検索中に、クエリと同じ平面の同じ側にいる隣人までの距離のみを考慮します。

 nbrs = NearestNeighbors(algorithm='brute', metric='cosine') nbrs.fit(model.wv.syn0norm) king_vec = model.wv['king'][np.newaxis, :] #              start = time.time() idxs = nbrs.kneighbors(king_vec, return_distance=False, n_neighbors=10)[0] print('full search time:', time.time() - start) print([model.wv.index2word[idx] for idx in idxs]) #  2          vec1_idx = random.randint(0, model.wv.syn0norm.shape[0]) vec2_idx = random.randint(0, model.wv.syn0norm.shape[0]) plane = model.wv.syn0norm[vec1_idx] - model.wv.syn0norm[vec2_idx] #     -,   . #             scalar = model.wv.syn0norm.dot(np.transpose(plane)) #                   if king_vec.dot(plane) > 0: mask = scalar > 0 else: mask = scalar < 0 print('elements in mask:', mask.sum()) half_nbrs = NearestNeighbors(algorithm='brute', metric='cosine') half_nbrs.fit(model.wv.syn0norm[mask]) half_index2word = list(compress(model.wv.index2word, mask)) start = time.time() idxs = half_nbrs.kneighbors(king_vec, return_distance=False, n_neighbors=10)[0] print('half search time:', time.time() - start) print([half_index2word[idx] for idx in idxs])

取得するもの：

  full search time: 20.3163180351 [u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'Prince_Paras'] elements in mask: 1961204 half search time: 9.15824007988 [u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'Prince_Paras']

そのため、計算を半分にして、飛行機のすぐ隣で正確に失いました。後で説明するアルゴリズムの中には、同様のトリックを使用するものがあります。

1. HNSW

2011年に、最高のナビゲーション可能なスモールワールド（NSW）の最近傍検索アルゴリズムの1つが公開されました。 2016年、彼の階層的可航小世界（HNSW）の後継者が登場しました。

NSW親アルゴリズムから始めましょう。「世界は狭い」というコラムに基づいています。これらのグラフには奇妙で便利な機能があります。頂点のペアはほとんど隣接していない可能性が高いですが、比較的少数のステップで到達可能です（ $\ログ{N}$ 平均して）。このようなグラフは非常に一般的です。たとえば、脳のニューラルネットワーク、ソーシャルメディアグループ、およびWordNetセマンティックネットワークはSWグラフです。この場合、頂点はベクトルであり、エッジはそれらを最も近い頂点に接続します。グラフには、遠距離のピークを結ぶエッジも表示されます。

近傍を検索するには、クエリまでの最短距離で頂点を検索してグラフを巡回します。ランダムな頂点から開始し、「友人」の未訪問の頂点（現在のエッジに接続されている頂点）からクエリまでの距離を考慮し、最短距離の頂点に移動します。長いエッジは、グラフにworld屈な世界の特性を与え、リクエストに近いオブジェクトの領域にすばやく移動できるようにし、短いエッジは最も近い隣人を熱心に検索します。

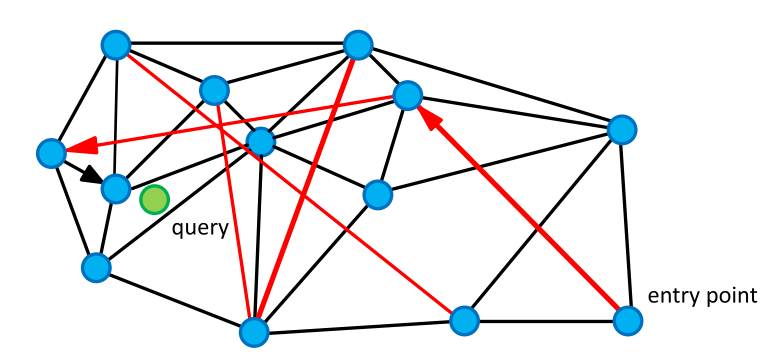
グラフを巡回する際に、最近傍の小さなリストを更新し、次の反復でリストが更新されていない場合は停止します。

擬似コード

 K-NNSearch(object q, integer: m, k) 1 TreeSet [object] tempRes, candidates, visitedSet, result 2 for (i←0; i < m; i++) do: 3 put random entry point in candidates 4 tempRes←null 5 repeat: 6 get element c closest from candidates to q 7 remove c from candidates 8 //check stop condition: 9 if c is further than k-th element from result 10 than break repeat 11 //update list of candidates: 12 for every element e from friends of c do: 13 if e is not in visitedSet than 14 add e to visitedSet, candidates, tempRes 15 16 end repeat 17 //aggregate the results: 18 add objects from tempRes to result 19 end for 20 return best k elements from result

 index = nmslib.init(space='cosinesimil', method='sw-graph') nmslib.addDataPointBatch(index, np.arange(model.wv.syn0.shape[0], dtype=np.int32), model.wv.syn0) index.createIndex({}, print_progress=True) start = time.time() items = nmslib.knnQuery(index, 10, king_vec.tolist()) print(time.time() - start) print([model.wv.index2word[idx] for idx in items])

取得するもの：

  0.000545024871826 [u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'royal']

Hierarchical Navigable Small World（HNSW）アルゴリズムでの上記のアイデアの開発を検討してください。これは多くの点でNSWに非常に似ていますが、現在はグラフの階層を扱っています。すべてのオブジェクトはゼロレイヤーで表され、レイヤーが大きくなったり小さくなったりするにつれて大きくなります。この場合、レイヤー上のすべてのオブジェクト $n + 1$ レイヤー上にあります $n$ 。

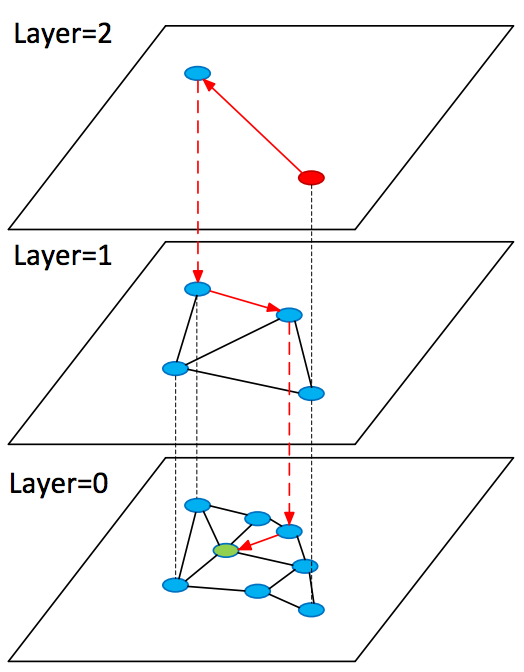
検索するとき、開始は上位層のグラフのランダムな頂点から発生し、そこで要求に近い頂点（候補）をすばやく見つけ、前の層でそれらから検索を再開します。

擬似コード

 SearchAtLayer (object q, Set[object] enterPoints, integer: M, ef, layer) 1 Set [object] visitedSet 2 priority_queue [object] candidates (closer - first), result (further - first) 3 candidates, visitedSet, result ← enterPoints 7 4 repeat: 5 object c =candidates.top() 6 candidates.pop() 7 //check stop condition: 8 if d(c,q)>d(result.top(),q) do: 9 break 10 //update list of candidates: 11 for_each object e from c.friends(layer) do: 12 if e is not in visitedSet do: 13 add e to visitedSet 14 if d(e, q)< d(result.top(),q) or result.size()<ef do: 15 add e to candidates, result 16 if result.size()>ef do: 17 result.pop() 18 return best k elements from result K-NNSearch (object query, integer: ef) 1 Set [object] tempRes, enterPoints=[enterpoint] 2 for i=maxLayer downto 1 do: 3 tempRes=SearchAtLayer (query, enterPoints, M, 1, i) 4 enterPoints =closest elements from tempRes 5 tempRes=SearchAtLayer (query, enterPoints, M, ef, 0) 6 return best K of tempRes

1.1。長所と短所

+アルゴリズムは理解しやすい

+最先端の結果を表示します

+ nmslibライブラリに効果的な実装があります

+グラフエッジを保存するための追加メモリコストが少ない

-このアルゴリズムはベクトル表現の圧縮をサポートしていません。これについてはさらに検討します

 index = nmslib.init(space='cosinesimil', method='hnsw') nmslib.addDataPointBatch(index, np.arange(model.wv.syn0.shape[0], dtype=np.int32), model.wv.syn0) index.createIndex({}, print_progress=True) start = time.time() items = nmslib.knnQuery(index, 10, king_vec.tolist()) print(time.time() - start) print([model.wv.index2word[idx] for idx in items])

取得するもの：

  0.000469923019409 [u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'Prince_Paras']

2. FAISS

2017年3月、FacebookはFANNライブラリであるANNのソリューションを紹介しました。多くの方法とアルゴリズムを組み合わせています。以下で検討するアルゴリズムでは、ベクトルのグループまでの距離は、それらの近くの基準点までの距離で近似されます。そのため、リクエストから少数のコントロールポイントまでの距離を見つけ、徹底的な検索により、リクエストの残りの部分により近いコントロールポイントに属するベクトルまでの距離を計算できます。このアルゴリズムを部分的に分析しましょう。

2.1。 ADC-非対称距離計算

次のアイデアをより詳細に考えてみましょう。ベクトルのグループまでの距離は、それらの近くの制御点までの距離で近似できます。アンカーポイントはスペースをエリアに分割します。 FAISSで参照点を検索するには、よく知られているk-meansクラスタリングアルゴリズムが使用され、得られた重心がベクトルと比較されます。

 （0.1、0.2）→1
 （0.5、-0.2）→2
 （0.1、0.1）→1
 （0.6、-0.1）→2

コレクションベクトルはその重心で近似されます $y \およそq_c（y）$ どこで $q_c：\ mathbb {R} ^ d \右矢印C_1 \サブセット\ mathbb {R} ^ d$ そして $C_1$ -多くの重心。次に、リクエストからの距離 $x$ 前に $y$ 近いかもしれません $d（x、y）\約d（x、q_c（y））$ 。距離を計算するこの方法は、非対称と呼ばれます。簡単に言えば、空間を領域に分割し、クエリから1つの領域に分類されるベクトルのグループまでの距離は、この領域を形成する重心までの距離にほぼ等しいと言いました。

重心に属するベクトルを効果的に保存し、すばやく検索することは、反転ファイルと呼ばれる簡単なトリックに役立ちます。

2.2。 IVF-反転ファイル

IVFでは、割り当てを逆にします。ベクトルのリストが重心に一致するようになりました。

 1→[（0.1、0.2）、（0.1、0.1）]
 2→[（0.5、-0.2）、（0.6、-0.1）]

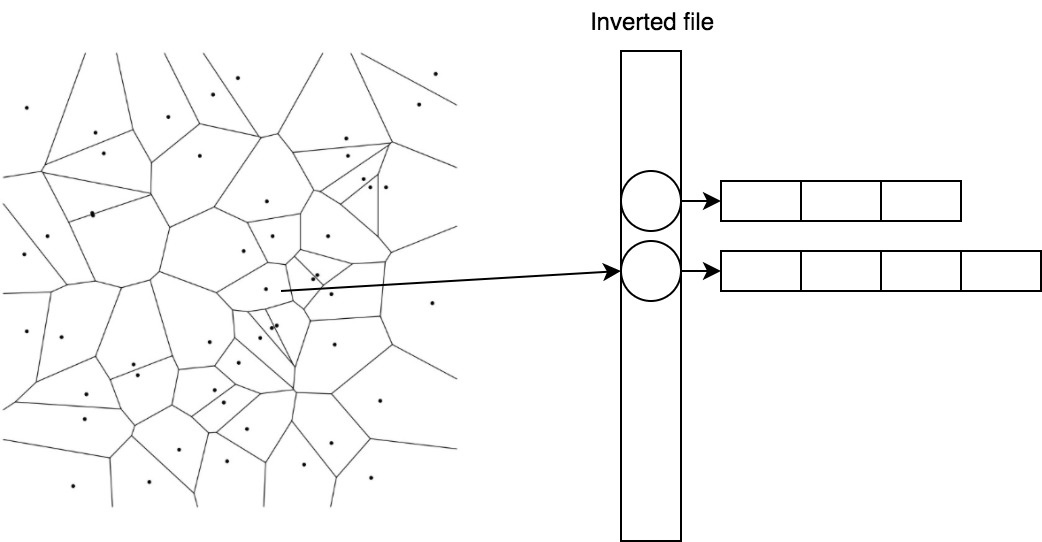
そのため、重心までの距離を計算することで候補をすばやく見つけて、最も近いものについて既に準備済みのリストを取得できます。

2.3。 PQ-製品量子化器

この記事で最後に触れるコンポーネントは、製品量子化器と呼ばれます。非可逆ベクトル圧縮を提供し、ベクトル表現がメモリに収まらない場合に使用されます。ベクトルの次元が128で、64ビット（コンポーネントあたり0.5ビットのみ）でエンコードしたい場合、重心の数に等しい量子化を処理する必要があります $k = 2 ^ {64}$ 。これは重要なタスクです。 $O（iknd）$ 、これには膨大なトレーニングセットも必要です。

ベクトルを分割して問題を単純化する $m$ 部品 $y_1、y_2、...、y_m \ in \ mathbb {R} ^ {d / m}$ 、および伝統により、各部品に256の重心があります。つまり、ベクトルは重心インデックスのセットとして書き換えることができます-例えば $（134、20、244、...、12）$ 、しかしこの経済は占める $m$ バイト

この種のコーディングを残差ベクトルに適用します $r（y）= y-q_c（y）$ 、 $r（y）\およそq_r（r（y））$ そして $y \およそq_c（y）+ q_r（y-q_c（y））$

2.4。検索する

そして今、これらすべてを1つのスキームにまとめます。

リクエスト用 $x$ 見つける $w$ 最も近い重心のうち、これらの重心に対応するベクトルのリストを収集し、残差ベクトルを使用してそれらまでの距離をカウントしてから、 $k$ 最も近い。

 import faiss index = faiss.index_factory(model.wv.syn0norm.shape[1], 'IVF16384,Flat') index.verbose = True train = model.wv.syn0norm[np.random.binomial(1, 1./3, size=model.wv.syn0norm.shape[0]).astype(bool)] index.train(train) index.add(model.wv.syn0norm) index.nprobe = 100 start = time.time() distances, items = index.search(king_vec, 10) print(time.time() - start) print([model.wv.index2word[idx] for idx in items[0]])

取得するもの：

  0.0048999786377 [u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'Prince_Paras']

2.5。長所と短所

+圧縮のサポート

+小さなセントロイドストレージのオーバーヘッド

+ GPUコンピューティング機能*

-CPUのHNSWより5倍遅い

* GPU実装をすぐに使用できなかったため、時間を無駄にしないことにしました。

3.いらいらする

スペースを平面で分割するという考えはAnnoyでうまく実装されています。アルゴリズムは、ブログで著者によって美しく説明されています。詳細を理解したい場合は、このアルゴリズムを読むことをお勧めします。その本質を要約してみます。このアルゴリズムでは、空間を平面で再帰的に分割し、二分木を形成します。ツリーの各ノードには、現在の平面を定義するベクトルが格納されます。検索するときは、ルートから開始し、プレーンに対するクエリの位置に基づいて子ノードを選択します。したがって、ツリーのリーフ要素に行きます。このリーフ要素は、プレーンのグループ（これは小さなスペースです）の片側にあるベクトルを格納します。これらは、必要な最近傍になりそうです。他のアルゴリズムと比較したAnnoyの長所と短所を見てみましょう。

3.1。長所と短所

+アルゴリズムは理解しやすい

-それは多くのメモリを必要とします

-速度の低下

4.アルゴリズムの比較

各アルゴリズムには、頂点のフレンドの最大数（NSW、HNSW）または重心の数（FAISS）のパラメーターのセットがあります。これらのパラメータは、消費されるメモリの量、検索の品質と速度に影響します。 Annoyの著者は、さまざまなパラメーターでannベンチマークリポジトリにANNアルゴリズムのグループのテストを実装しました。 GloVeおよびSIFTアルゴリズムを使用して取得したデータセット内の10個の最近傍の検索の精度を評価します。

GloVeは、単語のベクトル表現を取得する別の方法です;同じサイズのケースでトレーニングする場合、あらゆる点でword2vecを超えます。このデータセットは、20億のツイートでトレーニングされた120万の単語のベクトル表現で構成されています。 SIFTは、変換に耐性のある主要な画像ポイントとそのベクトル表現を取得するための古いアルゴリズムです。これはオブジェクト認識に使用され、この認識の重要な部分は同様のベクトル表現の検索でした。データセットにはいくつかのバリエーションがありますが、100万個のベクターを含むSIFT 1Mに興味があります。

以下は、アルゴリズムの速度と10個の最近傍の検索の精度との関係を示すグラフです。アルゴリズムはポイントのグループで表され、各ポイントは一連のパラメーターでテスト実行されます。

グローブ

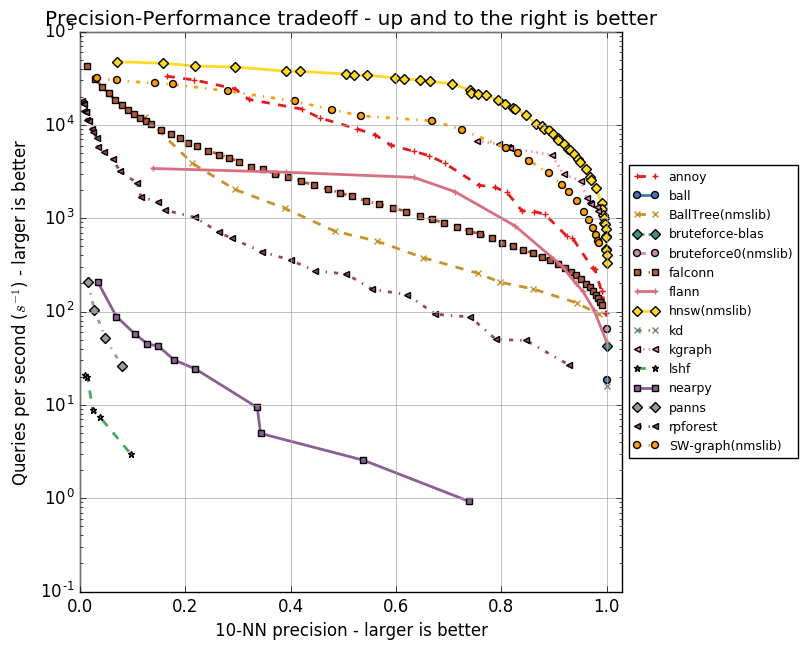
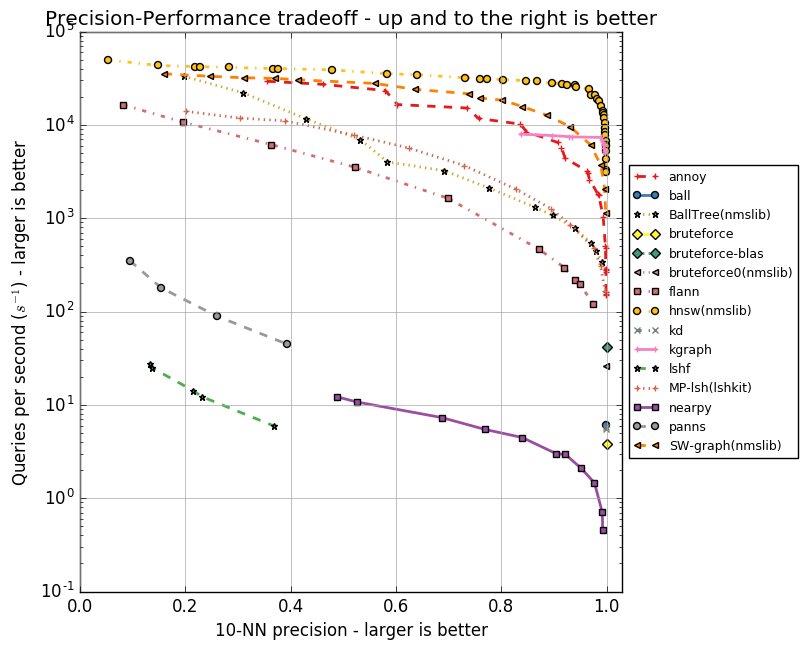
ふるいにかける

HNSWが自信を持ってリードしていることがわかります。ただし、グラフにはFAISSがありません。 Facebookは、異なる構成でHNSWとFAISSを個別に比較しました。結果を表に示します。

方法	検索時間	1-R @ 1	インデックスサイズ	インデックス作成時間
フラットCPU	9.100秒	1.0000	512 MB	0秒
nmslib（hnsw）	0.081秒	0.8195	512 + 796 MB	173秒
IVF16384、フラット	0.538秒	0.8980	512 + 8 MB	240秒
IVF16384、フラット（Titan X）	0.059秒	0.8145	512 + 8 MB	5秒
フラットGPU（Titan X）	0.753秒	0.9935	512 MB	0秒

表では、圧縮なしのFAISSメソッド、特にIVF16384,Flat

。したがって、16,384の重心を持つIVFADCが使用されます。 float32の次元128の百万ベクトルの場合のメモリコストが示されます。 HNSWは、CPUで計算する場合は5倍高速ですが、グラフのエッジ（ $32 * 2 * 4 * 1,000,000 / 1024 ^ 2 = $ 24$ ）重心よりも多くのメモリが必要です（ $16384 * 128 * 4/1024 ^ 2 = 8$ ）

5.まとめ

最近傍をすばやく見つけるために使用されるいくつかのアルゴリズムを調べました。アノイはメモリとスピードの両方を失いましたが、アイデアは良く、関連する問題の解決に役立ちます。たとえば、データセットのクリーニングに便利な隔離フォレストの異常検索アルゴリズムは、概念が非常に似ています。 FAISSはメモリに制限のある優れたソリューションであり、IVF16384、PQ64を使用して60 GBのRAMの10億個のベクトル表現を積み重ねることができます。ただし、メモリがボトルネックでない場合は、HNSWを選択する必要があります。

PS最も興味深い出版物は、FAISSのアルゴリズムに関するものでした。たとえば、GPUの最適化、量子化の改善された方法（最適化された製品の量子化）、インデックスを作成するためのトリッキーな方法（逆マルチインデックス）について読むことができます。

PPS私たち自身のために、HNSWを選択しました。

最近傍検索方法

1. HNSW

1.1。長所と短所

2. FAISS

2.1。 ADC-非対称距離計算

2.2。 IVF-反転ファイル

2.3。 PQ-製品量子化器

2.4。検索する

2.5。長所と短所

3.いらいらする

3.1。長所と短所

4.アルゴリズムの比較

5.まとめ

6.文学

More articles:

最近傍検索方法

1. HNSW

1.1。 長所と短所

2. FAISS

2.1。 ADC-非対称距離計算

2.2。 IVF-反転ファイル

2.3。 PQ-製品量子化器

2.4。 検索する

2.5。 長所と短所

3.いらいらする

3.1。 長所と短所

4.アルゴリズムの比較

5.まとめ

6.文学

More articles:

1.1。長所と短所

2.4。検索する

2.5。長所と短所

3.1。長所と短所