こんにちは私の名前はシリルで、ITマネージャーとして10年以上~~アルコール中毒~~者です。 MIPTで勉強しているときに、時々有料でコードを書きました。しかし、厳しい現実（あなたはお金を稼ぐ必要があり、できればそれ以上）に直面して、私は下り坂になりました。

しかし、すべてがそれほど悪いわけではありません！最近、パートナーと協力して、 Okdeskの顧客会計およびクライアントアプリケーションシステムというスタートアップの開発に完全に取り組んでいます。一方で-動きの方向を選択する際のより多くの自由。しかし一方で、「6か月間で3人の開発者が研究を行い、... 私たちは多くのことをしなければなりません。開発に関連するコア以外の実験（製品の主な機能に関連しない実験）を含みます。

そのような実験の1つは、パフォーマーのグループにさらにルーティングするために、テキストによってクライアントアプリケーションを分類するアルゴリズムの開発でした。この記事では、「非プログラマー」が1.5か月でバックグラウンドでpythonを習得し、実用的な利点がある簡単なMLアルゴリズムを記述する方法についてお話したいと思います。

勉強する方法は？

私の場合、コースラでの遠隔学習。機械学習や人工知能に関連する他の分野のコースは非常に多くあります。古典は、コースラの創設者であるアンドリュー・ウン（アンドリュー・ン）のコースと考えられています。しかし、このコースのマイナス点は（コースが英語であるという事実に加えて：これは万人向けではありません）、珍しいOctaveツールキット（MATLABの無料のアナログ）です。アルゴリズムを理解するために、これは主なことではありませんが、より一般的なツールから学ぶ方が良いです。

MIPTとYandexの専門分野である「機械学習とデータ分析」を選択しました（6つのコースがあります。記事に書かれていることは、最初の2つで十分です）。専門化の主な利点は、スラックの学生とメンターの活気のあるコミュニティです。1日のほとんどの時間に、質問に連絡できる人がいます。

機械学習とは何ですか？

記事の一部として、用語論争に飛び込むことはありません。したがって、数学的な精度が不十分な障害を見つけたい場合はご遠慮ください（私は品位の範囲を超えないことを約束します:)。

それでは、機械学習とは正確には何ですか？これは、知的人件費を必要とするがコンピューターを使用する問題を解決するための一連の方法です。機械学習方法の特徴は、前例（つまり、事前によく知られた正解がある例）で「トレーニング」されることです。

より数学的な定義は次のとおりです。

一連の特性を持つ多くのオブジェクトがあります。このセットを文字Xで示します。
多くの答えがあります。このセットを文字Yで示します。
複数のオブジェクトと複数の応答の間には（未知の）関係があります。すなわちセットXのオブジェクトをセットYのオブジェクトに関連付ける関数。関数yと呼びます。
Yからの回答が既知であるX （トレーニングセット）からのオブジェクトの有限サブセットがあります。
トレーニングサンプルによると、関数aを使用して、関数yをできるだけ近似する必要があります。関数aを使用して、 Xからの任意のオブジェクトがYから正しい答えを適切な確率（または数値の答えについて話している場合は精度）で取得するようにします。関数aの検索は、機械学習の問題です。

これが人生の例です。銀行はローンを提供します。銀行は、ローンの返済、返済なし、延滞返済など、結果がすでにわかっている借り手のプロファイルを多数蓄積しています。この例のオブジェクトは、記入済みの申請書を持つ借り手です。アンケートからのデータ-オブジェクトパラメータ。ローンの返済または未返済の事実は、オブジェクトに対する「応答」です（借り手のアンケート）。既知の結果を持つアンケートのセットは、トレーニングサンプルです。

借主のプロフィールで、潜在的な借り手によるローンの返済または非返済を予測できるようにしたいという自然な欲求があります。予測アルゴリズムを見つけることは機械学習タスクです。

機械学習タスクには多くの例があります。この記事では、テキストを分類するタスクについて詳しく説明します。

問題の声明

顧客サービス用のクラウドサービスであるOkdeskを開発していることを思い出してください。 Okdeskを業務に使用する企業は、クライアントポータル、メール、サイトからのWebフォーム、インスタントメッセンジャーなど、さまざまなチャネルを介してクライアントアプリケーションを受け入れます。アプリケーションは、1つまたは別のカテゴリに関連する場合があります。カテゴリに応じて、アプリケーションには1人または別のパフォーマーがいる場合があります。たとえば、1Cのアプリケーションはソリューションのために1Cの専門家に送信し、オフィスネットワークに関連するアプリケーションはシステム管理者のグループに送信する必要があります。

アプリケーションのフローを分類するために、ディスパッチャを選択できます。しかし、まず、お金がかかります（給与、税金、オフィスレンタル）。次に、アプリケーションの分類とルーティングに時間がかかり、アプリケーションは後で解決されます。内容に応じてアプリケーションを自動的に分類することができたら、それは素晴らしいことです！この問題を機械学習（および1人のITマネージャー）で解決してみましょう。

この実験では、分類された1200個のアプリケーションのサンプルが取得されました。サンプルでは、アプリケーションは14のカテゴリに分類されています。実験の目的：コンテンツに応じてアプリケーションを自動分類するメカニズムを開発します。これにより、ランダムなアプリケーションよりも何倍もの品質が得られます。実験の結果によれば、アルゴリズムの開発と、アプリケーションの分類に基づいた産業サービスの開発に関して決定を下す必要があります。

ツールキット

実験には、Lenovoラップトップ（コアi7、8GB RAM）、NumPy、Pandas、Scikit-learn、reライブラリ、 IPythonシェルを備えたPython 2.7プログラミング言語を使用しました。使用するライブラリについて詳しく説明します。

NumPy-大きな多次元数値配列で算術演算を実行するための多くの便利なメソッドとクラスを含むライブラリ。
Pandasは、データを簡単かつ自然に分析および視覚化し、それらに対して操作を実行できるライブラリです。主なデータ構造（オブジェクトタイプ）は、 Series （1次元構造）とDataFrame （2次元構造。実際には同じ長さの一連）です。
Scikit-learn-機械学習のほとんどの方法を実装するライブラリ。
Reは正規表現ライブラリです。正規表現は、テキスト分析に関連するタスクに不可欠なツールです。

Scikit-learnライブラリからは、いくつかのモジュールが必要になります。その目的は、資料のプレゼンテーションの過程で作成します。したがって、必要なすべてのライブラリとモジュールをインポートします。

import pandas as pd import numpy as np import re from sklearn import neighbors, model_selection, ensemble from sklearn.grid_search import GridSearchCV from sklearn.metrics import accuracy_score

そして、データの準備に進みます。

（インポートxxxのyyとしての構築は、xxxライブラリに接続していることを意味しますが、コードではyyを介してアクセスします）

データ準備

機械学習に関連する最初の（実験室ではなく）実際のタスクを解決するとき、アルゴリズムの学習（アルゴリズムの選択、パラメーターの選択、さまざまなアルゴリズムの品質の比較など）にほとんど時間を費やさないことがわかります。リソースの大部分は、データの収集、分析、準備に使用されます。

機械学習タスクのさまざまなクラスのデータを準備するためのさまざまな手法、方法、および推奨事項があります。しかし、ほとんどの専門家は、データの準備を科学ではなく芸術と呼びます。そのような表現もあります-機能エンジニアリング（つまり、オブジェクトを記述するパラメーターの構築）。

テキストを分類するタスクでは、機能に1つのオブジェクト-テキストがあります。機械学習アルゴリズムを彼に与えることは不可能です（私はすべてを知っているわけではありません:)。テキストは何らかの形でデジタル化し、形式化する必要があります。

実験の枠組みでは、テキストを形式化する原始的な方法が使用されました（しかし、それらは良い結果を示しました）。これについては後で説明します。

データの読み込み

初期データとして、1200のアプリケーションのアップロードがあることを思い出してください（14のカテゴリに不均等に分布しています）。各アプリケーションには、「件名」フィールド、「説明」フィールド、「カテゴリ」フィールドがあります。 [件名]フィールドはアプリケーションの短縮コンテンツであり、必須です。[説明]フィールドは拡張説明であり、空の場合があります。

データを.xlsxファイルからDataFrameにロードします。 .xlsxファイルには多くの列（実際のアプリケーションのパラメーター）がありますが、必要なのは「Subject」、「Description」、および「Category」のみです。

データをロードした後、「Subject」フィールドと「Description」フィールドを1つのフィールドに結合して、さらに処理しやすくします。これを行うには、最初にすべての空の説明フィールド（たとえば、空の文字列）を入力する必要があります。

 #   issues  DataFrame issues = pd.DataFrame() #   issues  Theme, Description  Cat,     ,     .xlsx . u'...' —   '…'  utf issues[['Theme', 'Description','Cat']] = pd.read_excel('issues.xlsx')[[u'', u'', u'']] #     Description   issues.Description.fillna('', inplace = True) #   Theme  Description (    )   Content issues['Content'] = issues.Theme + ' ' + issues.Description

したがって、DataFrameタイプのissue変数があります。この変数では、Content列（SubjectフィールドとDescriptionフィールドの結合フィールド）とCat（アプリケーションカテゴリ）を操作します。アプリケーションのコンテンツ（つまり、[コンテンツ]列）の形式化に進みます。

アプリケーションのコンテンツの形式化

形式化アプローチの説明

前述のように、最初のステップはアプリケーションテキストを形式化することです。次のように形式化します。

アプリケーションの内容を言葉に分解します。単語とは、区切り文字（ダッシュ、ハイフン、ピリオド、スペース、改行など）で区切られた2つ以上の文字のシーケンスを意味します。その結果、アプリケーションごとに、そのコンテンツに含まれる単語の配列を取得します。
セマンティックの負荷を持たない各アプリケーションから「寄生虫の単語」を除外します（たとえば、挨拶フレーズに含まれる単語：「hello」、「good」、「day」など）。
結果の配列から、辞書をコンパイルします。すべてのアプリケーションのコンテンツを記述するために使用される単語のセット。
次に、サイズ（アプリケーションの数） x （辞書内の単語の数 ）の行列を作成します。ここで、j番目の列のi番目のセルは、辞書のj番目の単語のi番目のアプリケーションのエントリの数に対応します。

請求項4のマトリックスは、申請内容の形式化された記述である。数学的には、行列の各行は、辞書空間内の対応するアプリケーションのベクトルの座標です。アルゴリズムをトレーニングするには、結果のマトリックスを使用します。

重要なポイント ：p。3は、トレーニングセットからアルゴリズム（テストセット）の品質管理用のランダムサブサンプルを選択した後に実行されます。これは、新しいデータでアルゴリズムが「戦闘中」に表示する品質をよりよく理解するために必要です（たとえば、トレーニングサンプルで完全に正しい答えを与えるアルゴリズムを実装することは難しくありませんが、新しいデータランダムではうまく機能しません）：この状況はリトレーニングと呼ばれます）。辞書をコンパイルする直前にテストサンプルを分離することは重要です。テストデータを含む辞書をコンパイルする場合、サンプルでトレーニングされたアルゴリズムは未知のオブジェクトに精通しているからです。未知のデータでの品質に関する結論は正しくありません。

次に、p.p。 1-4のコードを見てください。

コンテンツを単語に分割し、単語の寄生虫を削除します

まず、すべてのテキストを小文字にします（「プリンター」と「プリンター」-人に対してのみ同じ言葉を使用しますが、機械に対しては使用しません）：

 #       def lower(str): return str.lower() #      Content issues['Content'] = issues.Content.apply(lower)

次に、「寄生虫の言葉」の補助辞書を定義します（その充填は、アプリケーションの特定のサンプルの反復実験によって実行されました）。

 garbagelist = [u'', u'', u'', u'', u'',u'', u'', u'', u'']

各アプリケーションのテキストを2文字以上の長さの単語に分割し、「寄生単語」を除く結果の単語を配列に含める関数を宣言します。

 def splitstring(str): words = [] #     [] for i in re.split('[;,.,\n,\s,:,-,+,(,),=,/,«,»,@,\d,!,?,"]',str): #  ""  2    if len(i) > 1: #  - if i in garbagelist: None else: words.append(i) return words

正規表現ライブラリreとそのsplitメソッドは、区切り文字でテキストを単語に分割するために使用されます。区切り文字の配列がsplitメソッド（区切り文字のセットが反復的に補充された）と分割される文字列に渡されます。

宣言された関数を各アプリケーションに適用します。出力では、元のDataFrameを取得します。このDataFrameには、各アプリケーションを構成する単語の配列（「寄生単語」を除く）を含む新しいWords列が表示されます。

 issues['Words'] = issues.Content.apply(splitstring)

辞書を作成します

次に、すべてのアプリケーションのコンテンツに含まれる単語の辞書のコンパイルを開始します。しかしその前に、上で書いたように、トレーニングサンプルをコントロールサンプル（「テスト」、「遅延」とも呼ばれます）とアルゴリズムをトレーニングするサンプルに分割します。

選択の分離は、 Scikit-learnライブラリーのmodel_selectionモジュールのtrain_test_splitメソッドによって実行されます。データを含む配列（アプリケーションテキスト）、ラベルを含む配列（アプリケーションカテゴリ）、およびテストサンプルのサイズ（通常は全体の30％）をメソッドに渡します。出力では、トレーニング用のデータ、トレーニング用のラベル、制御用のデータ、制御用のラベルの4つのオブジェクトを取得します。

 issues_train, issues_test, labels_train, labels_test = model_selection.train_test_split(issues.Words, issues.Cat, test_size = 0.3)

ここで、トレーニング用に残されたデータ（ issues_train ）を使用して辞書をコンパイルする関数を宣言し、このデータに関数を適用します。

 def WordsDic(dataset): WD = [] for i in dataset.index: for j in xrange(len(dataset[i])): if dataset[i][j] in WD: None else: WD.append(dataset[i][j]) return WD #    words = WordsDic(issues_train)

そのため、トレーニングサンプルのすべてのアプリケーションのテキストを構成する単語の辞書を作成しました（アプリケーションは制御用に残されています）。辞書は可変ワードに書き込まれました。単語配列のサイズは12015番目の要素（つまり単語）であることが判明しました。

アプリケーションのコンテンツを辞書スペースに翻訳します

トレーニング用のデータを準備する最終ステップに移りましょう。つまり、サイズマトリックス（サンプルのアプリケーションの数） x （辞書の単語の数）を構成します 。ここで、j番目の列のi番目の行は、サンプルのi番目のアプリケーションの辞書のj番目の単語の出現数です。

 #   len(issues_train)  len(words),    train_matrix = np.zeros((len(issues_train),len(words))) # ,   [i][j]   j-   words  i-    for i in xrange(train_matrix.shape[0]): for j in issues_train[issues_train.index[i]]: if j in words: train_matrix[i][words.index(j)]+=1

これで、トレーニングに必要なすべてのものがあります： train_matrixマトリックス（すべてのアプリケーション用にコンパイルされた辞書空間のアプリケーションに対応するベクトルの座標形式のアプリケーションの形式化されたコンテンツ）およびlabels_train （トレーニング用に残されたサンプルからのアプリケーションのカテゴリ）。

トレーニング

ラベル付きデータ（つまり、正しい答えがわかっているデータ： labels_trainのtrain_matrix行列）のトレーニングアルゴリズムに移りましょう。ほとんどの機械学習メソッドはScikit-learnライブラリに実装されているため、このセクションにはほとんどコードがありません。それらの方法の開発は、材料を習得するのに役立つかもしれませんが、実用的な観点からは、この必要はありません。

以下では、機械学習の特定の方法の原則を簡単な言語で述べようとします。

最適なアルゴリズムを選択する原則について

どの機械学習アルゴリズムが特定のデータで最良の結果をもたらすかは決してわかりません。しかし、問題を理解すれば、既存のすべてのアルゴリズムを通過しないように、最適なアルゴリズムのセットを決定できます。問題を解決するために使用される機械学習アルゴリズムの選択は、トレーニングセットのアルゴリズムの品質を比較することによって実行されます。

アルゴリズムの品質と見なされるものは、解決する問題によって異なります。品質メトリックの選択は、別の大きなトピックです。アプリケーション分類の一環として、単純なメトリックである精度が選択されました。精度は、アルゴリズムが正しい答えを与えた（アプリケーションの正しいカテゴリを入力した）サンプル内のオブジェクトの割合として定義されます。したがって、アプリケーションのカテゴリをより正確に予測できるアルゴリズムを選択します。

アルゴリズムハイパーパラメーターなどの概念について言うことが重要です。機械学習アルゴリズムには、作業の品質を決定する外部（つまり、トレーニングセットから分析的に導出できないもの）パラメーターがあります。たとえば、オブジェクト間の距離を計算する必要があるアルゴリズムでは、距離は異なることを意味する場合があります。マンハッタン距離、古典的なユークリッド距離などです。

各機械学習アルゴリズムには、独自のハイパーパラメーターセットがあります。奇妙なことに、ハイパーパラメーターの最適な値の選択は列挙によって実行されます。パラメーター値の各組み合わせに対して、アルゴリズムの品質が計算され、値の最適な組み合わせがこのアルゴリズムに使用されます。このプロセスは、コンピューティングの観点からはコストがかかりますが、どこに行くべきですか。

相互検証は、ハイパーパラメーターの各組み合わせでアルゴリズムの品質を決定するために使用されます。それが何であるか説明させてください。トレーニングサンプルは、N個の等しい部分に分割されます。アルゴリズムは、N-1個の部分のサブサンプルで順次トレーニングされ、品質は1つの遅延で考慮されます。その結果、N個の部分はそれぞれ、品質のカウントに1回、アルゴリズムの学習にN-1回使用されます。パラメーターの組み合わせでのアルゴリズムの品質は、相互検証中に取得された品質値間の平均と見なされます。取得した品質値をより信頼できるように、相互検証が必要です（平均化するとき、特定のサンプルパーティションの考えられる「スキュー」を平準化します）。どこでもう少し詳しく知っています。

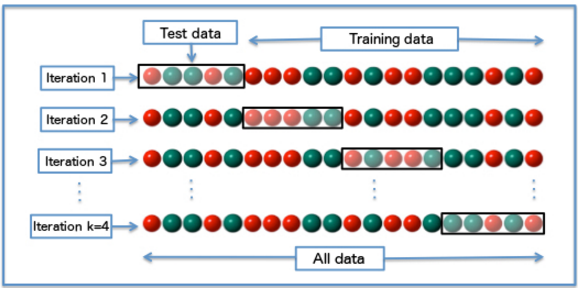
相互検証の概念を示すすウィキペディアの画像

したがって、各アルゴリズムに最適なアルゴリズムを選択するには：

ハイパーパラメーター値の可能なすべての組み合わせが整理されます（各アルゴリズムには、ハイパーパラメーターとその値の独自のセットがあります）。
相互検証を使用したハイパーパラメーター値の組み合わせごとに、アルゴリズムの品質が計算されます。
そのアルゴリズムは、最高の品質を示すハイパーパラメーター値の組み合わせで選択されます。

上記のアルゴリズムのプログラミングの観点からは、複雑なことは何もありません。しかし、これは必要ありません。 Scikit-learnライブラリーには、グリッドに従ってパラメーターを選択するための既製のメソッドがあります（ grid_searchモジュールのGridSearchCVメソッド）。必要なのは、アルゴリズム、パラメータグリッド、および数N（クロス検証のためにサンプルを分割する部分の数。これらは「折り畳み」とも呼ばれます）をメソッドに転送することです。

問題の解決の一環として、2つのアルゴリズムが選択されました：k最近傍とランダムツリーの構成。それぞれについて、以下のストーリーがあります。

k最近傍（kNN）

k最近傍法が最も簡単に理解できます。以下で構成されています。

トレーニングサンプルがあり、そのデータは既に正式化されています（トレーニングの準備ができています）。つまり、オブジェクトはある空間のベクトルとして表されます。私たちの場合、アプリケーションは辞書空間のベクトルとして提示されます。トレーニングセットの各ベクトルについて、正しい答えがわかっています。

新しいオブジェクトごとに、このオブジェクトとトレーニングセットのオブジェクト間のペアワイズ距離が計算されます。次に、トレーニングセットからk個の最も近いオブジェクトが取得され、k個の最も近いオブジェクトのサブサンプルで優先される回答が新しいオブジェクトに対して返されます（数を予測する必要があるタスクの場合、k最も近い値から平均値を取得できます）。

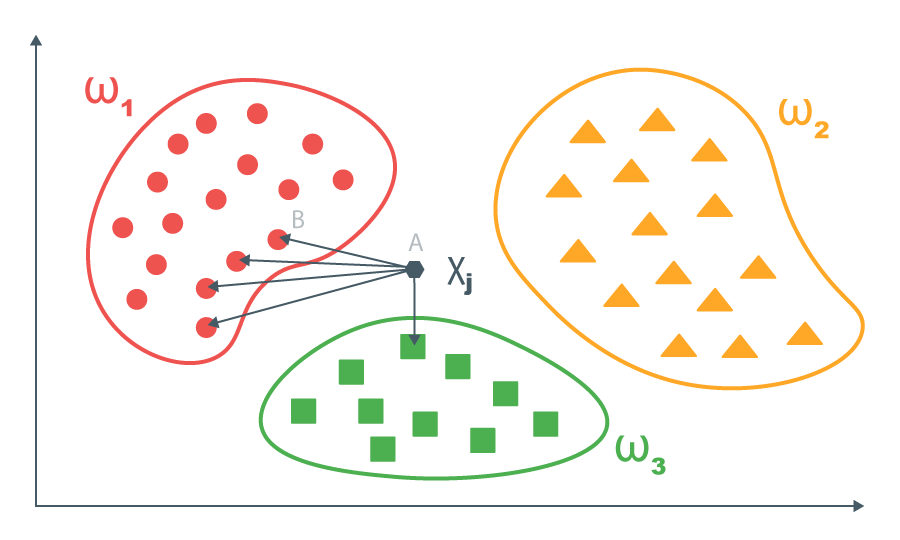
最近傍のメソッドkの図

アルゴリズムを開発することができます：より近いオブジェクトのラベルの値により大きな重みを与えるため。ただし、アプリケーションを分類するタスクについては、これを行いません。

この問題のフレームワークにおけるアルゴリズムのハイパーパラメーターは、数k（結論付ける最近傍の数）と距離の決定です。 1〜7の範囲で近傍の数を選択し、マンハッタン距離（座標差のモジュラスの合計）とユークリッド距離（座標差の平方和のルート）からの距離を選択します。

簡単なコードを実行します。

 %%time #     param_grid = {'n_neighbors': np.arange(1,8), 'p': [1,2]} #  fold-  - cv = 3 #  estimator_kNN = neighbors.KNeighborsClassifier() # ,    fold-       optimazer_kNN = GridSearchCV(estimator_kNN, param_grid, cv = cv) #        optimazer_kNN.fit(train_matrix, labels_train) #         print optimazer_kNN.best_score_ print optimazer_kNN.best_params_

2分40秒後、マンハッタン距離によって決定される3つの最近傍のアルゴリズムにより、最高品質の53.23％が表示されることがわかります。

ランダムツリー構成

決定的な木

決定木は別の機械学習アルゴリズムです。アルゴリズムのトレーニングは、何らかの理由で、トレーニングサンプルを段階的に（通常は2つに分割しますが、通常は必要ありません）に分割します。決定木の仕組みを示す簡単な例を次に示します。

決定木には、内部頂点（サンプルをさらに分割することで決定が行われる）と最終頂点（シート）があり、そこに落ちたオブジェクトを予測するために使用されます。

決定的な頂点で、単純な条件がチェックされます。条件x ^jへのオブジェクトの何らかの（これについては）j番目の特徴の対応は、何らかのt以上です。条件を満たすオブジェクトは一方のブランチに送信され、もう一方のブランチには送信されません。

アルゴリズムを学習する際、すべての頂点に1つのオブジェクトが残るまでトレーニングセットを分割することが可能です。このアプローチは、トレーニングサンプルでは優れた結果をもたらしますが、未知のデータでは「ハット」が発生します。したがって、いわゆる「停止基準」を決定することが重要です-頂点がリーフになり、この頂点のさらなる分岐が中断される条件。停止基準はタスクに依存します。ここにはいくつかのタイプの基準があります。最上部のオブジェクトの最小数とツリーの深さの制限です。この問題を解決するために、頂点内のオブジェクトの最小数の基準が使用されました。オブジェクトの最小数に等しい数は、アルゴリズムのハイパーパラメーターです。

新しい（予測を必要とする）オブジェクトは、トレーニングされたツリーを介して実行され、対応するシートに分類されます。リスト内のオブジェクトに対して、次の答えを示します。

分類の問題については、このシートのトレーニングセットで最も一般的なオブジェクトのクラスを返します。
回帰問題（つまり、答えが数値である問題）の場合、このシートからトレーニングサンプルのオブジェクトの平均値を返します。

各頂点の属性jの選択方法（ツリーの特定の頂点でサンプルをどの属性で分割するか）と、この属性に対応するしきい値tについては引き続き説明します。このために、いわゆるエラー基準Q（X _m 、j、t）が導入されます。ご覧のように、エラー基準は、サンプルX _m （問題の頂点に到達したトレーニングサンプルの部分）、サンプルX _mが問題の頂点で分割されるパラメーターj、およびしきい値tに依存します。エラー基準が最小になるようにjとtを選択する必要があります。各トレーニングセットのjおよびtの値の可能なセットは限られているため、列挙によって問題は解決されます。

エラー基準とは何ですか？この場所の記事のドラフト版には、多くの公式と付随する説明、情報コンテンツ基準とその特殊なケース（ジニー基準とエントロピー基準）についてのストーリーがありました。しかし、記事は非常に肥大化しました。手続きと数学を理解したい人は、インターネット上のすべてについて読むことができます（たとえば、ここ）。私は指の「物理的意味」に自分自身を制限します。エラー基準は、分割後に取得されたサブサンプル内のオブジェクトの「多様性」のレベルを示します。分類問題の「多様性」とは、さまざまなクラスを意味し、回帰問題（数値が予測される）では分散を意味します。したがって、サンプルをサンプリングするとき、結果のサブサンプルの「多様性」を最小限に抑える必要があります。

木を見つけました。木の構成に移りましょう。

決定的なツリーの構成

決定木は、トレーニングセットの非常に複雑なパターンを明らかにすることができます。 , — . ().

N “”. (, ) , — ( N ) .

, N . : N . : / (.. , ). — (.. , ; , — ). .

- ! 2- : ( ) ( ).

:

 %%time #     param_grid = {'n_estimators': np.arange(20,101,10), 'min_samples_split': np.arange(4,11, 1)} #  fold-  - cv = 3 #  estimator_tree = ensemble.RandomForestClassifier() # ,    fold-       optimazer_tree = GridSearchCV(estimator_tree, param_grid, cv = cv) #        optimazer_tree.fit(train_matrix, labels_train) #         print optimazer_tree.best_score_ print optimazer_tree.best_params_

3 30 , 65,82% 60 , 4.

結果

(, — ) .

test_matrix, , (.. , train_matrix, ).

 #   len(issues_test)  len(words) test_matrix = np.zeros((len(issues_test),len(words))) # ,   [i][j]   j-   words  i-    for i in xrange(test_matrix.shape[0]): for j in issues_test[issues_test.index[i]]: if j in words: test_matrix[i][words.index(j)]+=1

accuracy_score metrics Scikit-learn. :

 print u' :', accuracy_score(optimazer_tree.best_estimator_.predict(test_matrix), labels_test) print u'kNN:', accuracy_score(optimazer_kNN.best_estimator_.predict(test_matrix), labels_test)

51,39% k 73,46% .

""

, “ ” , random. “” , random. , “” , - .

3- “” :

random;
;
Random, .

random 14 100/14 * 100% = 7,14% . , 14,5% ( ). random- . , random-:

 #  random import random # ,    random-  rand_ans = [] # for i in xrange(test_matrix.shape[0]): rand_ans.append(labels_train[labels_train.index[random.randint(0,len(labels_train))]]) #  print u' random:', accuracy_score(rand_ans, labels_test)

14,52%.

, , “” . やった！

次は？

, 90% — . , . “” ( , ). -, (: " ", " ", " " ..) — ( ) .

, : . " " "", . . , , , .

, Okdesk .

"! !" （c）

( 2). .

「非プログラマ」の手による機械学習：クライアントアプリケーションのテクニカルサポートへの分類（パート1）