
「再帰を理解するには、まず再帰を理解する必要があります」
特にプログラミングの初心者にとって、再帰は理解が難しい場合があります。 簡単に言えば、再帰は自分自身を呼び出す関数です。 しかし、例を使って説明してみましょう。
あなたが寝室のドアを開こうとしていると想像してください、そしてそれは閉じられています。 あなたの3歳の息子が角を曲がって現れ、唯一の鍵は箱の中に隠されていると言います。 あなたは仕事に遅れており、本当に部屋に入ってシャツを着る必要があります。
箱を開くのは、見つけるためだけです...さらに箱を探します。 箱は箱の中にあり、どれが鍵なのかわかりません。 早急にシャツが必要なので、適切なアルゴリズムを考え出し、鍵を見つける必要があります。
この問題を解決するアルゴリズムを作成するには、反復と再帰の2つの主なアプローチがあります。 これらのアプローチのフローチャートは次のとおりです。
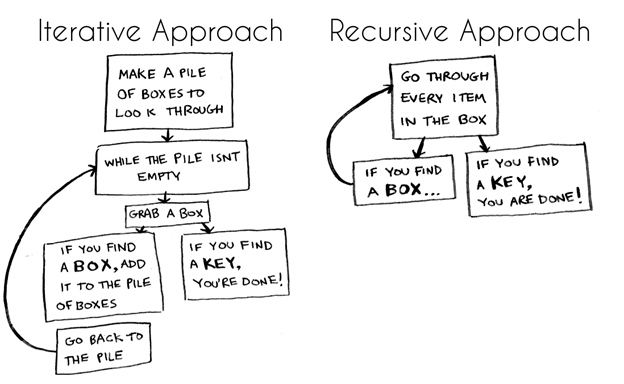
あなたにとってどちらのアプローチが簡単ですか?
最初のアプローチでは、whileループを使用します。 すなわち ボックスのスタックがいっぱいになっている間に、次のボックスをつかんで中を見てください。 以下は、何が起こっているのかを反映したJavascript擬似コードです(擬似コードはコードとして記述されていますが、人間の言語に似ています)。
function look_for_key(main_box) { let pile = main_box.make_a_pile_to_look_through(); while (pile is not empty) { box = pile.grab_a_box(); for (item in box) { if (item.is_a_box()) { pile.append(item) } else if (item.is_a_key()) { console.log("found the key!") } } } }
別のアプローチでは、再帰を使用します。 再帰とは、関数がそれ自体を呼び出すことです。 擬似コードの2番目のオプションは次のとおりです。
function look_for_key(box) { for (item in box) { if (item.is_a_box()) { look_for_key(item); } else if (item.is_a_key()) { console.log("found the key!") } } }
どちらのアプローチも同じことを行います。 再帰的アプローチを使用する主なポイントは、理解すれば簡単に読むことができるということです。 実際には、再帰を使用してもパフォーマンスは向上しません。 ループを使用した反復アプローチの方が高速な場合もありますが、再帰の単純さが望ましい場合があります。
再帰は多くのアルゴリズムで使用されるため、その仕組みを理解することが重要です。 それでも再帰が簡単に思えない場合でも、心配しないでください。もう少し例を見ていきます。
境界と再帰の場合
再帰関数を記述するときに考慮する必要があるのは、無限ループです。 関数がそれ自体を呼び出すとき...そして決して停止することはできません。
カウント関数を作成するとします。 次のように、Javascriptで再帰的に記述できます。
// WARNING: This function contains an infinite loop! function countdown(i) { console.log(i) countdown(i - 1) } countdown(5); // This is the initial call to the function.
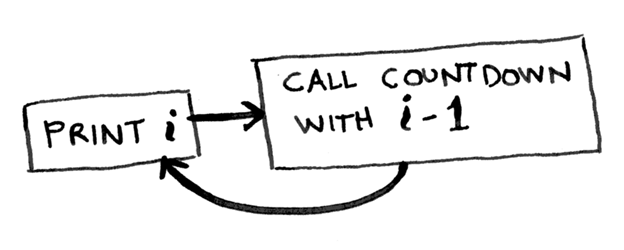
この関数は無期限にカウントされます。 したがって、無限ループでコードを突然実行した場合は、Ctrl-Cショートカットで停止します。 (または、たとえばCodePenで作業する場合、URLの最後に「?Turn_off_js = true」を追加することでこれを実行できます。)
再帰関数は、いつ停止する必要があるかを常に知っている必要があります。 再帰関数には常に2つのケースがあります:再帰ケースと境界ケースです。 再帰的な場合とは、関数がそれ自体を呼び出すことであり、境界となる場合とは、関数がそれ自体を呼び出すのをやめることです。 境界ケースが存在すると、ループが防止されます。
繰り返しますが、カウント関数は、境界の場合のみです:
function countdown(i) { console.log(i) if (i <= 1) { // base case return; } else { // recursive case countdown(i - 1) } } countdown(5); // This is the initial call to the function.
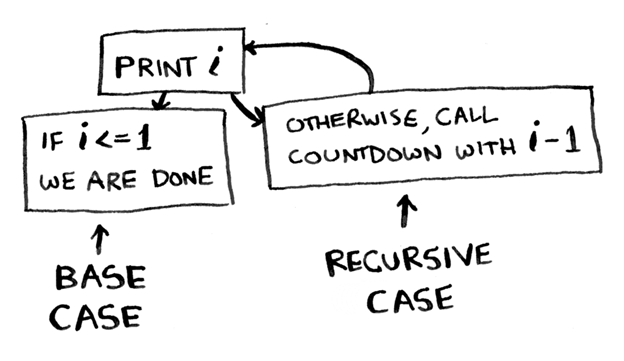
この関数で何が起こるかは完全には明らかではありません。 関数を呼び出して5を渡すとどうなるかを説明します。
最初に、 Console.Logコマンドを使用して5番を印刷します。 なぜなら 5が1以下ではない場合、 elseブロックに進みます。 ここで、関数を再度呼び出して、4を渡します(5-1 = 4から)。
4を出力します。また、 iは 1以下ではないため、 elseブロックに移動して3を渡します。これは、 iが1になるまで続きます。これが発生すると、コンソールに1を出力します。 1と等しい。最後に、キーワードreturnを使用してブロックに入り、関数を終了します。
呼び出し履歴
再帰関数は、いわゆる呼び出しスタックを使用します。 プログラムが関数を呼び出すと、関数は呼び出しスタックの最上部に送信されます。 これは書籍の山のようなもので、一度に1つずつ追加します。 その後、何かを取り戻す準備ができたら、常に一番上の要素を取り去ります。
階乗カウント機能を使用して、コールスタックの動作を示します。 階乗(5)は5! 5と計算されます! = 5 * 4 * 3 * 2 * 1 。 数値の階乗を計算する再帰関数は次のとおりです。
function fact(x) { if (x == 1) { return 1; } else { return x * fact(x-1); } }
それでは、 fact(3)を呼び出すとどうなるか見てみましょう。 以下は、スタックで何が起こっているかを段階的に示す図です。 スタックの一番上のボックスは、現在停止しているファクト関数を何を呼び出すかを示しています。

ファクト関数の各呼び出しには、xの独自のコピーがどのように含まれているかに注意してください。 これは、再帰が機能するための非常に重要な条件です。 xから関数の別のコピーにアクセスすることはできません。
キーをすでに見つけましたか?
ボックス内のキーを見つける最初の例に戻りましょう。 最初の方法は、ループを使用した反復アプローチだったことを覚えていますか? このアプローチでは、検索用のボックスのスタックを作成するため、まだ検索していないボックスを常に把握できます。
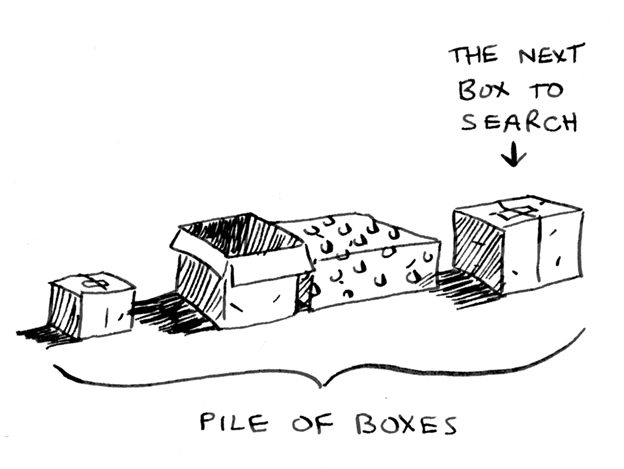
しかし、再帰的なアプローチにはスタックはありません。 それでは、アルゴリズムはどのボックスを探すべきかをどのように理解しますか? 回答:「ボックスのスタック」はスタックに保存されます。 スタックは、関数の半分実行された呼び出しで構成され、各呼び出しには、表示用の独自の半分完成したボックスのリストが含まれています。 スタックはボックスのスタックを追跡します!
そして、再帰のおかげで、ようやく鍵を見つけてシャツを手に入れることができました!
また、5分間の再帰ビデオを見ることができます。 ここで紹介する概念の理解を深める必要があります。
著者からの結論
願わくば、この記事がプログラミングの再帰についての理解をもう少し明確にしてくれることを願っています。 この記事は、私の新しいManning PublicationsビデオコースのAlgorithms in Motionというレッスンに基づいています。 コースも記事も、Adit Bhargavaが執筆したすばらしい本「Grokking Algorithms」に従って書かれました。
そして最後に、再帰の知識を真に統合するために、少なくともこの記事をもう一度読んでください。
私自身も、ボーカルズの記事やビデオチュートリアルを興味を持って見ていることを付け加えたいと思います。この記事、特にA. BhargavのGrokking Algorithmsからのこれらの本当に素晴らしいイラストも気に入っていただければ幸いです。