パート1：ドット、ベクトル、および基本原則

最大のプロジェクトで使用されている最新の3次元ゲームエンジンは、数学とプログラミングの微妙な組み合わせです。 多くのゲームプログラマは、それらを完全に理解することは非常に難しいと認めています。 十分な経験（または私のような専門教育）がない場合、このタスクはさらに難しくなります。 3Dエンジングラフィックスシステムの基本を紹介します。



このパートでは、ポイントとベクトル、およびそれらに関連する興味深いすべてを検討します。 代数の基礎（変数と変数の数学）とコンピューターサイエンス（オブジェクト指向言語の基礎）を知っているなら、この記事を理解できます。 ただし、いくつかのトピックは非常に複雑になることに留意してください。

基本座標系

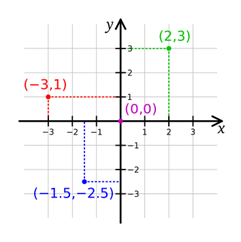
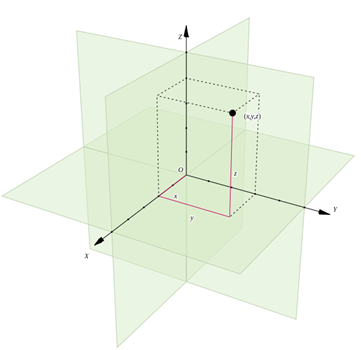
基本から始めましょう。 3次元グラフィックスには、3次元空間の概念が必要です。 ほとんどの場合、すべてのタイプのスペースで、デカルト空間が使用されます。これにより、デカルト座標を使用できます（標準表記 $$$（x、y）$ ほとんどの学校で研究されている2次元グラフィックス）。





多くの学生の生活を害する呪い



3次元デカルト空間は、x、y、およびz軸を提供します（水平、垂直、および深度の位置を記述）。 この空間内の任意の点の座標は、いくつかの数字として指定されます（この場合、3つの軸があるため、3つの数字です）。 2次元平面では、エントリは $$$（x、y）$ 、および3次元空間-として $$$（x、y、z）$ 。 このエントリ（ tuple ）は、スペースの開始点（通常は $$$（0,0,0）$ 。



ヒント：タプルは、コンピューターサイエンスまたは数学の要素の順序付きリスト（またはシーケンス）です。 それは記録です $$$（K、y、l、e）$ 私の名前を構成する文字のシーケンスを示す4要素のタプルになります。







この空間では、ポイントを3つの要素のタプルとして定義します。 これは次のように説明できます。

$$

$$P =（x、y、z）$$

ポイントを設定することに加えて、その部分を決定する必要があります。



タプルの各要素は、 基底ベクトルに沿った位置を決定するスカラー数です。 各基底ベクトルには単位長（その長さは1）が必要です。つまり、次のようなタプルです。 $$$（1,1,1）$ そして $$$（2,2,2）$ 長すぎるため、ベースベクトルにすることはできません。



空間に3つの基底ベクトルを定義します。

$$

$$\ begin {aligned} X＆=（1,0,0）\\ Y＆=（0,1,0）\\ Z＆=（0,0,1）\ end {aligned}$$

出典：http://www.thefullwiki.org/Arithmetics/Cartesian_Coordinate。

---

座標系

次に、座標系の数学的定義、グラフィックスシステムへの影響、および実行可能な計算について説明します。

ポイント指定

座標系の原点は点で示されます $$$O$ 、3つの要素のタプル（0,0,0）で記述されます。 つまり、座標系の数学的表現は次のように表現できます。

$$

$$\ {O; X、Y、Z \}$$

このエントリを使用すると、 $$$（x、y、z）$ 原点に対する点の位置を表します。 そのような定義は、 $$$P$ 、 $$$（a、b、c）$ 次のように表すことができます。

$$

$$P = O + aX + bY + cZ$$

これからは、スカラー値を小文字で、ベクトルを大文字で示します。 $$$a$ 、 $$$b$ そして $$$c$ スカラーであり、 $$$X$ 、 $$$Y$ そして $$$Z$ -ベクトル。 （実際、これらは上記で定義した基本的なベクトルです。）



これは、タプル（2,3,4）によって記録されたポイントが次のように表現できることを意味します。

$$

$$\ begin {aligned}（2,3,4）＆=（2,0,0）+（0,3,0）+（0,0,4）\\＆=（0,0,0）+ （2,0,0）+（0,3,0）+（0,0,4）\\＆=（0,0,0）+ 2（1,0,0）+ 3（0,1、 0）+ 4（0,0,1）\\＆= O + 2X + 3Y + 4Z \\ \ end {aligned}$$

そこで、「3次元空間のポイント」という抽象概念を採用し、4つのオブジェクトの合計として定義しました。 このような定義は、コードで概念を実装する際に非常に重要になります。

相互垂直性

使用する座標系には非常に価値のある特性があります。それは相互垂直性です。 これは、それぞれの平面上の各軸の交点で、それらの間の角度が90度であることを意味します。







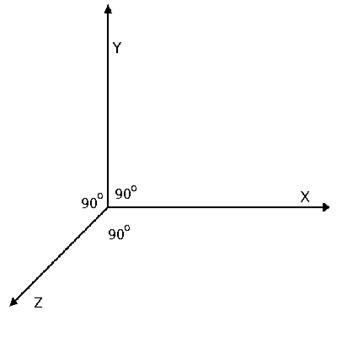
座標系は「正しい」とも呼ばれます。





ソース： http : //viz.aset.psu.edu/gho/sem_notes/3d_fundamentals/html/3d_coordinates.html



数学の言語では、これは次のことを意味します。

$$

$$X = Y \倍Z$$

どこで $$$\回$ はベクトル積演算子を示します。



ベクトル積は、次の式で定義できます（3つの要素の2つのタプルがある場合）。

$$

$$（a、b、c）\ times（d、e、f）=（bf-ce、cd-af、ae-bd）$$

これらの式は退屈に見えるかもしれませんが、後で多くの異なる計算と変換を実行しやすくなります。 幸いなことに、ゲームエンジンを作成するとき、これらすべての方程式を覚える必要はありません。これらの式から始めて、その上にそれほど複雑でないシステムを構築できます。 少なくとも、エンジンの基本的な何かを変更するまでは！

---

ドットとベクトル

座標系の基本を決定したら、ポイントとベクトルについて、そしてさらに重要なことには、それらが互いにどのように相互作用するかについて話し合うことができます。 まず、ポイントとベクトルは完全に異なるオブジェクトであることに注意する価値があります。ポイントは空間内の物理的な場所であり、ベクトルは2つのポイント間の空間です。







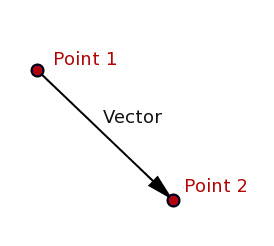
これらの2種類のオブジェクトを混同しないように、ポイントを斜体で大文字で書きます。たとえば、 $$$P$ 、およびベクトル-太字の大文字で、たとえば $$$\ mathbf {V}$ 。



点とベクトルを扱う場合、2つの主要な公理を使用します。 ここにあります：

• 公理1：2点間の差はベクトル、つまり $$$\ mathbf {V} = P-Q$
• 公理2：点とベクトルの合計は点です。 $$$Q = P + \ mathbf {V}$

ヒント： 公理とは、証拠なしに受け入れられるほど十分に明白であると考えられる論理的記述です。

---

エンジン作成

これら2つの公理のおかげで、 Point



クラスとVector



クラスという3次元ゲームエンジンの心臓部である「ブリック」クラスを作成するのに十分な情報があります。 この情報に基づいて独自のエンジンを作成する場合、これらのクラスを作成するときに他の重要な手順を実行する必要があります（主に既存のAPIの最適化と操作に関連します）が、簡略化のためにこれを省略します。



クラスの例はすべて擬似コードで記述されるため、お気に入りの言語で実装できます。 2つのクラスのスケッチを次に示します。

 Point Class { Variables: num tuple[3]; //(x,y,z) Operators: Point AddVectorToPoint(Vector); Point SubtractVectorFromPoint(Vector); Vector SubtractPointFromPoint(Point); Function: //      API,   //      drawPoint; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 Vector Class { Variables: num tuple[3]; //(x,y,z) Operators: Vector AddVectorToVector(Vector); Vector SubtractVectorFromVector(Vector); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

演習として、これらのクラスの各関数に（上記で説明した内容に基づいて）作業コードを追加してみてください。 これが完了したら、次の簡単なプログラムを実行して作業をテストします。

 main { var point1 = new Point(1,2,1); var point2 = new Point(0,4,4); var vector1 = new Vector(2,0,0); var vector2; point1.drawPoint(); //  (1,2,1) point2.drawPoint(); //  (0,4,4) vector2 = point1.subtractPointFromPoint(point2); vector1 = vector1.addVectorToVector(vector2); point1.addVectorToPoint(vector1); point1.drawPoint(); //  (4,0,-2) point2.subtractVectorFromPoint(vector2); point2.drawPoint(); //  (-1,6,7) }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

---

おわりに

最初のパートは終わりました！ ここでは、2つのクラスを記述するためだけに多くの数学が使用されているようですが、実際はそうです。 ほとんどの場合、そのレベルでゲームを操作する必要はありませんが、ゲームエンジンの内部動作の詳細を知ることは（少なくともあなた自身の喜びのために）依然として有用です。

パート2：線形変換

次に、回転やスケールなどのベクトルのプロパティを変更できる線形変換について説明します。 すでに作成したクラスにそれらを適用する方法を学びます。



線形変換について説明するには、Pointクラスを少し変更する必要があります。コンソールにデータを出力する代わりに、便利なグラフィックAPIを使用して、関数が画面に現在のポイントを描画するようにします。

---

線形変換の基本

単なる警告です。線形変換の方程式は、実際よりもずっと複雑に見えます。 三角法を使用しますが、三角法演算の実行方法を実際に知る必要はありません。各関数に渡す必要があるものとその関数から受け取るものを説明します。また、中間アクションについては、電卓または数学ライブラリを使用できます。



ヒント：これらの方程式の内部動作をより深く理解したい場合は、 このビデオを見て 、 このPDFを読んでください 。



すべての線形変換は次の形式を取ります。

$$

$$B = F（A）$$

このことから、変換機能があることが明らかです $$$F（）$ 、ベクトルは入力として使用されます $$$A$ 、出力でベクトルを取得します $$$B$ 。



これらの各部分（2つのベクトルと関数）は、行列として表すことができます。ベクトル $$$B$ -1x3行列として、ベクトル $$$A$ -別の1x3行列、および線形変換として $$$F（）$ -3x3 マトリックス （ 変換マトリックス ）として。



つまり、方程式を展開すると、次のようになります。

$$

$$\ begin {bmatrix} b_ {0} \\ b_ {1} \\ b_ {2} \ end {bmatrix} = \ begin {bmatrix} f_ {00}＆f_ {01}＆f_ {02} \\ f_ {10}＆f_ {11}＆f_ {12} \\ f_ {20}＆f_ {21}＆f_ {22} \ end {bmatrix} \ begin {bmatrix} a_ {0} \\ a_ {1} \ \ a_ {2} \ end {bmatrix}$$

三角法や線形代数を経た場合、すでに行列演算の悪夢を思い出すかもしれません。 幸いなことに、この式を書いてほとんどの問題を取り除く簡単な方法があります。 次のようになります。

$$

$$\ begin {bmatrix} b_ {0} \\ b_ {1} \\ b_ {2} \ end {bmatrix} = \ begin {bmatrix} f_ {00} a_ {0} + f_ {01} a_ {1} + f_ {02} a_ {2} \\ f_ {10} a_ {0} + f_ {11} a_ {1} + f_ {12} a_ {2} \\ f_ {20} a_ {0} + f_ { 21} a_ {1} + f_ {22} a_ {2} \\ \ end {bmatrix}$$

ただし、ベクトルとその回転量を指定する必要がある場合、回転の場合のように、これらの方程式は入力データの2番目のソースの存在下で変化する可能性があります。 ターンの仕組みを見てみましょう。

---

ターン

定義上、回転とは、ターニングポイントを中心としたオブジェクトの円運動です。 空間のピボットポイントは、XY平面、XZ平面、またはYZ平面に属することができます（各平面は、最初の部分で説明した2つの基底ベクトルで構成されます）。







3つのピボットポイントは、3つの独立した回転行列があることを意味します。



XY回転行列：

$$

$$\ begin {bmatrix} cos \ theta＆-sin \ theta＆0 \\ sin \ theta＆cos \ theta＆0 \\ 0＆0＆1 \\ \ end {bmatrix}$$

XZ回転行列：

$$

$$\ begin {bmatrix} cos \ theta＆0＆sin \ theta \\ 0＆1＆0 \\ -sin \ theta＆0＆cos \ theta \ end {bmatrix}$$

YZ回転行列：

$$

$$\ begin {bmatrix} 1＆0＆0 \\ 0＆cos \ theta＆-sin \ theta \\ 0＆sin \ theta＆cos \ theta \ end {bmatrix}$$

つまり、ポイントを回転させる $$$A$ XY平面の周りに90度（ $$$\ pi / 2$ ラジアン-ほとんどの数学ライブラリには、度をラジアンに変換する機能があります）、次の手順を実行する必要があります。

$$

$$\ begin {aligned} \ begin {bmatrix} b_ {0} \\ b_ {1} \\ b_ {2} \ end {bmatrix}＆= \ begin {bmatrix} cos \ frac {\ pi} {2}＆ -sin \ frac {\ pi} {2}＆0 \\ sin \ frac {\ pi} {2}＆cos \ frac {\ pi} {2}＆0 \\ 0＆0＆1 \ end {bmatrix} \ begin {bmatrix} a_ {0} \\ a_ {1} \\ a_ {2} \ end {bmatrix} \\＆= \ begin {bmatrix} cos \ frac {\ pi} {2} a_ {0} + -sin \ frac {\ pi} {2} a_ {1} + 0a_ {2} \\ sin \ frac {\ pi} {2} a_ {0} + cos \ frac {\ pi} {2} a_ {1 } + 0a_ {2} \\ 0a_ {0} + 0a_ {1} + 1a_ {2} \ end {bmatrix} \\＆= \ begin {bmatrix} 0a_ {0} + -1a_ {1} + 0a_ {2 } \\ 1a_ {0} + 0a_ {1} + 0a_ {2} \\ 0a_ {0} + 0a_ {1} + 1a_ {2} \ end {bmatrix} \\＆= \ begin {bmatrix} -a_ { 1} \\ a_ {0} \\ a_ {2} \ end {bmatrix} \ end {aligned}$$

つまり、出発点が $$$A$ 座標を持っていた $$$（3,4,5）$ その後、出口点 $$$B$ 座標を持つことになります $$$（-4,3,5）$ 。

演習：関数の回転

練習として、 Vector



クラスの3つの新しい関数を作成してみてください。 1つはベクトルをXY平面の周りに回転させ、もう1つはYZの周りに回転させ、3番目はXZの周りに回転させます。 入力では、関数は目的の回転数を受け取り、出力ではベクトルを返す必要があります。



一般的に、関数は次のように機能します。

1. 出力ベクトルを作成します。
2. 度単位の入力をラジアンに変換します。
3. 上記の方程式を使用して、出力ベクトルのタプルの各要素を解きます。
4. 出力ベクトルを返します。

---

スケーリング

スケーリングは、指定されたスケールに従ってオブジェクトを拡大または縮小する変換です。



この変換は非常に簡単です（少なくともターンと比較して）。 スケーリング変換には、 入力ベクトルと、空間の各軸に沿った入力ベクトルのスケールを決定する3つの要素のスケーリングタプルという2種類の入力データが必要です。



たとえば、ズームタプルでは $$$（s_ {0}、s_ {1}、s_ {2}）$ 価値 $$$s_ {0}$ x軸のスケールを表し、 $$$s_ {1}$ -y軸に沿って、 $$$s_ {2}$ -Z軸に沿って。



スケール変換行列の形式は次のとおりです（ここで、 $$$s_ {0}$ 、 $$$s_ {1}$ そして $$$s_ {2}$ スケーリングのタプルの要素です）：

$$

$$\ begin {bmatrix} s0＆0＆0 \\ 0＆s1＆0 \\ 0＆0＆s2 \ end {bmatrix}$$

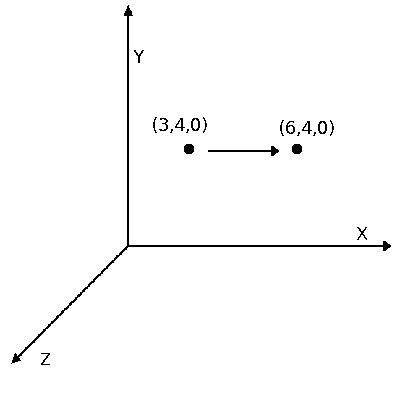
入力ベクトルAを作成するには $$$（a_ {0}、a_ {1}、a_ {2}）$ x軸の2倍（つまり、タプルを使用 $$$S =（2、1、1）$ ）、計算の形式は次のとおりです。

$$

$$\ begin {aligned} \ begin {bmatrix} b_ {0} \\ b_ {1} \\ b_ {2} \ end {bmatrix}＆= \ begin {bmatrix} s0＆0＆0 \\ 0＆s1＆ 0 \\ 0＆0＆s2 \ end {bmatrix} \ begin {bmatrix} a_ {0} \\ a_ {1} \\ a_ {2} \ end {bmatrix} \\＆= \ begin {bmatrix} 2＆ 0＆0 \\ 0＆1＆0 \\ 0＆0＆1 \ end {bmatrix} \ begin {bmatrix} a_ {0} \\ a_ {1} \\ a_ {2} \ end {bmatrix} \\ ＆= \ begin {bmatrix} 2a_ {0} + 0a_ {1} + 0a_ {2} \\ 0a_ {0} + 1a_ {1} + 0a_ {2} \\ 0a_ {0} + 0a_ {1} + 1a_ {2} \ end {bmatrix} \\＆= \ begin {bmatrix} 2a_ {0} \\ a_ {1} \\ a_ {2} \ end {bmatrix} \ end {aligned}$$

つまり、入力ベクトルで $$$A =（3,4,0）$ 出力ベクトル $$$B$ 等しくなります $$$（6,4,0）$ 。

演習：ズーム機能

別の演習として、Vectorクラスに新しい関数を追加します。 この新しい関数はスケーリングタプルを受け取り、出力ベクトルを返す必要があります。



一般に、関数は次のように機能するはずです。

1. 出力ベクトルを作成します。
2. 上記の方程式（ y0 = x0 * s0; y1 = x1*s1; y2 = x2*s2
   
   
   
   簡略化できます）を使用した出力ベクトルのタプルの各要素の解。
3. 出力ベクトルを返します。

---

何かを作りましょう！

自由に線形変換ができるようになったので、新しい機能を示す小さなプログラムを作成しましょう。 画面上にポイントのグループを描画し、それらを全体として変更し、線形変換を実行できるプログラムを作成します。



始める前に、 Point



クラスに別の関数を追加する必要があります。 これをsetPointToPoint()



と呼び、単に渡されたポイントに現在のポイントの位置を設定します。 入り口で、彼女はポイントを受け取り、何も返しません。



プログラムの簡単な特徴を次に示します。

• プログラムは、100ポイントを配列に保存します。
• Dキーを押すと、プログラムは現在の画面をクリアし、ポイントを再描画します。
• Aキーを押すと、プログラムはすべてのポイントの位置を0.5倍にします。
• Sキーを押すと、プログラムはすべてのポイントの位置を2.0倍にします。
• Rキーを押すと、XY平面上ですべてのポイントの位置が15度回転します。
• Escapeキーを押すと、プログラムが閉じます（JavaScriptまたは別のWeb指向言語で記述しない場合）。

私たちが持っているクラスは次のとおりです。

 Point Class { Variables: num tuple[3]; //(x,y,z) Operators: Point AddVectorToPoint(Vector); Point SubtractVectorFromPoint(Vector); Vector SubtractPointFromPoint(Point); //        Null SetPointToPoint(Point); Functions: //          API drawPoint; } Vector Class { Variables: num tuple[3]; //(x,y,z) Operators: Vector AddVectorToVector(Vector); Vector SubtractVectorFromVector(Vector); Vector RotateXY(degrees); Vector RotateYZ(degrees); Vector RotateXZ(degrees); Vector Scale(s0,s1,s2); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

与えられた要件でコードがどのように見えるか見てみましょう：

 main{ //   API //   (   ) //   100  Point Array pointArray[100]; for (int x = 0; x < pointArray.length; x++) { //      pointArray[x].tuple = [random(0,screenWidth), random(0,screenHeight), random(0,desiredDepth)); } //         function redrawScreen() { //      API ClearTheScreen(); for (int x = 0; x < pointArray.length; x++) { //     pointArray[x].drawPoint(); } } //     escape,    while (esc != pressed) { //        if (key('d') == pressed) { redrawScreen(); } if (key('a') == pressed) { //      Point origin = new Point(0,0,0); Vector tempVector; for (int x = 0; x < pointArray.length; x++) { //         tempVector = pointArray[x].subtractPointFromPoint(origin); // ,       pointArray[x].setPointToPoint(origin); //          pointArray[x].addVectorToPoint(tempVector.scale(0.5,0.5,0.5)); } redrawScreen(); } if(key('s') == pressed) { //      Point origin = new Point(0,0,0); Vector tempVector; for (int x = 0; x < pointArray.length; x++) { //         tempVector = pointArray[x].subtractPointFromPoint(origin); // ,       pointArray[x].setPointToPoint(origin); //          pointArray[x].addVectorToPoint(tempVector.scale(2.0,2.0,2.0)); } redrawScreen(); } if(key('r') == pressed) { //      Point origin = new Point(0,0,0); Vector tempVector; for (int x = 0; x < pointArray.length; x++) { //         tempVector = pointArray[x].subtractPointFromPoint(origin); // ,       pointArray[x].setPointToPoint(origin); //          pointArray[x].addVectorToPoint(tempVector.rotateXY(15)); } redrawScreen(); } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

それで、私たちはすべての新しい機能を示す短い良いプログラムを手に入れました！

---

おわりに

すべての可能な線形変換を検討したわけではありませんが、マイクロモーターは形になり始めています。



いつものように、簡単にするために、エンジンからいくつかのもの（つまり、移動と反射）を削除しました。 これら2つのタイプの線形変換について詳しく知りたい場合は、 Wikipediaの記事と記事内のリンクを参照してください。



次のパートでは、範囲外のさまざまな表示スペースとクリッピングオブジェクトについて検討します。

パート3：スペースとクリッピング

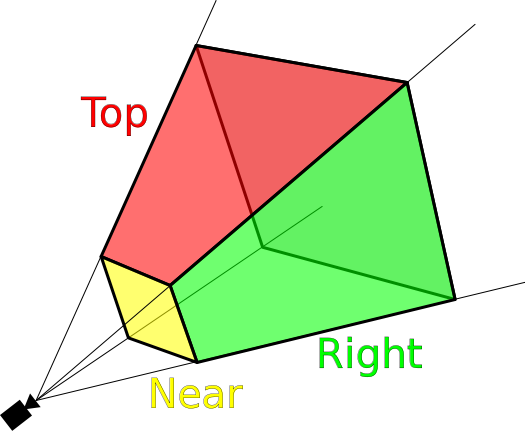
独自に作成した2つのクラスの使用はかなり複雑なプロセスですが、さらに、可能な各ポイントを描画するとシステムメモリがすぐに使い果たされることがわかります。 これらの問題を解決するために、ゲームエンジンに新しいクラスを追加します： カメラ 。



レンダリングはカメラ内でのみ行われ、すべてのオブジェクトを画面サイズに合わせて切り取り 、すべてのポイントを制御します。



しかし、これらすべてを始める前に、クリッピングについて話し始める必要があります。

---

クリッピング

定義上、クリッピングは、オブジェクトのより大きなグループからのオブジェクトの選択です。 ゲームエンジンでは、小さなグループが画面に描画する必要があるポイントになります。 オブジェクトの大きなグループは、既存のすべてのポイントのセットになります。



クリッピングのおかげで、エンジンはシステムメモリの消費を大幅に削減します。 彼はプレイヤーが見ることができるものだけを描き、ポイントの全世界を描きません。 エンジンでは、表示スペースのパラメーターを設定してこれを実装します。



表示スペースは、x、y、zの3つの従来の軸すべてに沿って定義されます。 xの境界線は、ウィンドウの左右の境界線の間のすべて、yの境界線-ウィンドウの上下の境界線の間のすべてから構成され、zの境界線は0



（カメラがインストールされている）からプレーヤーの可視距離（デモでは）任意に選択した値100



を使用します）。



ポイントをレンダリングする前に、カメラクラスはポイントが表示スペースにあるかどうかを確認します。 そうである場合、ポイントが描画され、そうでない場合は描画されません。

---

たぶん、カメラを追加する時ですか？

クリッピングの基本を理解したら、カメラクラスを作成できます。

 Camera Class { Vars: int minX, maxX; //    X int minY, maxY; //.  .  Y int minZ, maxZ; //.  .  Z }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

また、エンジンでレンダリングするプロセス全体をカメラに配置します。 多くの場合、エンジンでは、レンダラーはカメラシステムから分離されています。 一部のエンジンでは、システムを一緒に格納すると混乱が生じるため、これは通常、カプセル化システムの利便性のために行われます。 ただし、チュートリアルでは、それらを単一のシステムとして扱う方が簡単です。



まず、シーンを描画するためにクラスの外部から呼び出すことができる関数が必要です。 この関数は、既存のすべてのポイントを循環し、それらをカメラのクリッピングパラメーターと比較し、条件下でそれらを描画します。





ソース： http : //en.wikipedia.org/wiki/File : ViewFrustum.svg



ヒント：カメラシステムをレンダラーから分離する場合は、 Renderer



クラスを作成し、カメラシステムでポイントを切り取り、配列に描画する必要があるものを保存し、レンダラーのrender draw()



関数に配列を送信します。

---

ポイント管理

カメラクラスの最後の部分は、ポイント管理システムです。 使用するプログラミング言語に応じて、これは単にレンダリング用のすべてのオブジェクトの配列（後でポイントだけでなく処理します）になるか、デフォルトでオブジェクトの親クラスの使用が必要になる場合があります。 選択が非常に不運な場合は、オブジェクトの親クラスを独自に実装し、レンダリングされたすべてのクラス（これまでは単なるドット）がこのクラスを継承するようにする必要があります。



制御システムをクラスに追加すると、カメラは次のようになります。

 Camera Class { Vars: int minX, maxX; //    X int minY, maxY; //    Y int minZ, maxZ; //    Z array objectsInWorld; //    Functions: null drawScene(); //     ,    }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これらすべての追加を行ったので、最後の部分で書かれたプログラムを少し改善しましょう。

---

大きくて良い

最後のパートで作成したプログラム例に基づいて、簡単なポイントレンダリングプログラムを作成します。



プログラムのこの反復では、新しいカメラクラスの使用を追加します。 Dキーを押すと、プログラムはクリッピングせずに画面を再描画し、画面の右上隅にレンダリングされたオブジェクトの数を表示します。 Cキーを押すと、プログラムはクリッピング画面を再描画し、レンダリングされたオブジェクトの数も表示します。



コードを見てみましょう。

 main{ //   API //   (   ) var camera = new Camera(); //    camera.objectsInWorld[100]; //   100     //    camera.minX = 0; camera.maxX = screenWidth; camera.minY = 0; camera.maxY = screenHeight; camera.minZ = 0; camera.maxZ = 100; for(int x = 0; x < camera.objectsInWorld.length; x++) { //      camera.objectsInWorld[x].tuple = [random(-200,1000), random(-200,1000), random(-100,200)); } function redrawScreenWithoutCulling() //         { ClearTheScreen(); //      API for(int x = 0; x < camera.objectsInWorld.length; x++) { camera.objectsInWorld[x].drawPoint(); //     } } while(esc != pressed) //   { if(key('d') == pressed) { redrawScreenWithoutCulling(); } if(key('c') == pressed) { camera.drawScene(); } if(key('a') == pressed) { Point origin = new Point(0,0,0); Vector tempVector; for(int x = 0; x < camera.objectsInWorld.length; x++) { //         tempVector = camera.objectsInWorld[x].subtractPointFromPoint(origin); // ,       camera.objectsInWorld[x].setPointToPoint(origin); //          camera.objectsInWorld[x].addVectorToPoint(tempVector.scale(0.5,0.5,0.5)); } } if(key('s') == pressed) { Point origin = new Point(0,0,0); //create the space's origin as a point Vector tempVector; for(int x = 0; x < camera.objectsInWorld.length; x++) { //         tempVector = camera.objectsInWorld[x].subtractPointFromPoint(origin); // ,       camera.objectsInWorld[x].setPointToPoint(origin); //          camera.objectsInWorld[x].addVectorToPoint(tempVector.scale(2.0,2.0,2.0)); } } if(key('r') == pressed) { Point origin = new Point(0,0,0); //create the space's origin as a point Vector tempVector; for(int x = 0; x < camera.objectsInWorld.length; x++) { //         tempVector = camera.objectsInWorld[x].subtractPointFromPoint(origin); // ,       camera.objectsInWorld[x].setPointToPoint(origin); //          camera.objectsInWorld[x].addVectorToPoint(tempVector.rotateXY(15)); } } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、クリッピングのすべての力を自分の目で見ることができます！サンプルコードでは、デモのWeb互換性を高めるためにいくつかの実装が少し異なることに注意してください。

---

おわりに

カメラとレンダリングシステムを作成したので、技術的には既製の3次元ゲームエンジンがあると言えます。彼はあまり印象的ではありませんが、すべてに時間があります。



次のパートでは、エンジンに幾何学的図形（つまり、線分と円）を追加する方法を学習し、それらの方程式を画面ピクセルに適用するために使用できるアルゴリズムについて説明します。

パート4：線分と円のラスタライズ

ラスタライズ

ラスタライズは、ベクターグラフィック形式（またはこの場合は数学的に）で記述されたフォームを、（フォームがピクセル構造に適合する）ラスタイメージに変換するプロセスです。



数学はコンピュータグラフィックスに必要なほど正確ではない場合があるため、アルゴリズムを使用して、それが記述する画面を整数スクリーンに適合させる必要があります。たとえば、数学では、ポイントは座標内にある場合があります$$（3.2 、4.6 ）が、レンダリングは、それを移動させる必要があります$(3.2, 4.6)$$$（3 、5 ）が表示画素構造に合うようにします。フォームの各タイプには、独自のラスタライズアルゴリズムがあります。ラスタライズする最も単純なフォーム、ラインセグメントから始めましょう。$(3, 5)$

---

線分

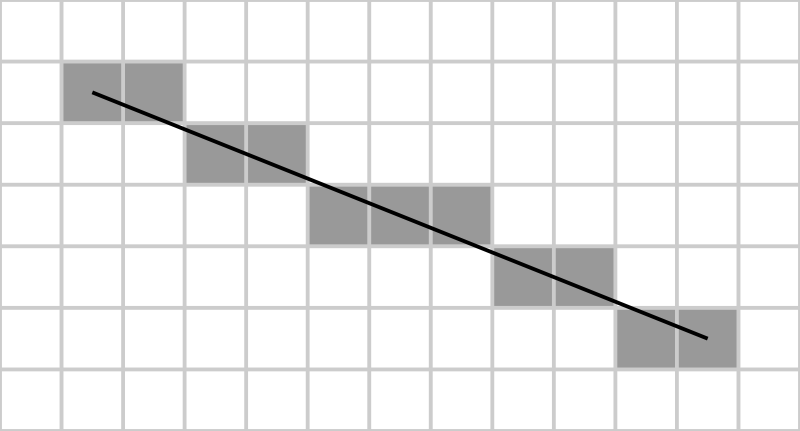
出典：http : //en.wikipedia.org/wiki/File : Bresenham.svg



線分は最も単純な描写形式の1つであるため、これは多くの場合、幾何学で研究された最初の概念の1つです。それらは、2つの別々の点（開始点と終了点）とそれらを結ぶ線で記述されます。線分をラスタライズするために最も一般的に使用されるアルゴリズムは、ブレゼンハムアルゴリズムと呼ばれます。



Bresenhamのアルゴリズムの手順は次のようになります。

1. 線分セグメントの開始点と終了点の入力を取得します。
2. プロパティを計算して線分セグメントの方向を決定する $$$dx$ そして $$$dy$ （ $$$dx = x_{1} - x_{0}$ 、 $$$dy = y_{1} - y_{0}$ ）
3. 特性の決意sx
   
   
   
   、sy
   
   
   
   及びエラー検出（数学的な定義は以下のとおりです）。
4. セグメント内の各ポイントを上下のピクセルに丸めます。

Bresenhamアルゴリズムを実装する前に、エンジンで使用できる基本セグメントクラスを作成しましょう。

 LineSegment Class { Variables: int startX, startY; //   int endX, endY; //   Function: array returnPointsInSegment; // ,     }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

新しいクラスを使用して変換を実行する必要がある場合LineSegment



は、対応する変換を開始点と終了点に適用し、LineSegment



それらをクラスに戻すだけで十分です。LineSegment



Bresenhamアルゴリズムは、後続のすべてのポイントを検索するために開始ポイントと終了ポイントのみを必要とするため、ライン間のすべてのポイントは描画中に処理されます。既存のエンジンに



クラスを埋め込むには、クラスLineSegment



に関数を追加する必要draw()



があるため、関数の使用を拒否しましたreturnPointsInSegment



。この関数は、ラインセグメントにあるすべてのポイントの配列を返します。これにより、セグメントを簡単に描画およびカットできます。



関数returnPointsInSegment()



は次のようになります（JavaScriptで）。

 function returnPointsInSegment() { //        var pointArray = new Array(); //          var x0 = this.startX; var y0 = this.startY; var x1 = this.endX; var y1 = this.endY; //     ,     var dx = Math.abs(x1-x0); var dy = Math.abs(y1-y0); var sx = (x0 & x1) ? 1 : -1; //  x var sy = (y0 & y1) ? 1 : -1; //  y var err = dx-dy; //    //     pointArray.push(new Point(x0,y0)); //   while(!((x0 == x1) && (y0 == y1))) { var e2 = err * 2; //   //    ,       (  ) if(e2 => -dy) { err -= dy; x0 += sx; } if(e2 < dx) { err += dx; y0 += sy; } //     pointArray.push(new Point(x0, y0)); } return pointArray; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

カメラクラスにラインセグメントのレンダリングを追加する最も簡単な方法はif



、たとえば次のような単純な構造を追加することです。

  //     if (class type == Point) { //    } else if (class type == LineSegment) { var segmentArray = LineSegment.returnPointsInSegment(); //     ,    ,     }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、それが私たちのファーストクラスフォームの作業に必要なすべてです！Bresenhamアルゴリズムの技術的な側面（特にエラー）について詳しく知りたい場合は、Wikipediaの記事でそれらについて読むことができます。

---

サークル

出典：http : //en.wikipedia.org/wiki/File:



Bresenham_circle.svg円のラスタライズは、線分のラスタライズよりも少し複雑です。ほとんどの作業では、円の中心点にアルゴリズムを使用します。これは、ブレゼンハムアルゴリズムの開発です。つまり、類似した段階で構成されていますが、いくつかの違いがあります。



新しいアルゴリズムは次のように機能します。

1. 中心点と円の半径を取得します。
2. 各主方向の強制ポイント
3. 各象限の周りをループし、弧を描きます

circleクラスはline segmentクラスに非常に似ており、次のようになります。

 Circle Class { Variables: int centerX, centerY; //   int radius; //  Function: array returnPointsInCircle; // ,    Circle }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この関数returnPointsInCircle()



は、クラス関数のように動作LineSegment



し、カメラがレンダリングして切り取ることができるようにポイントの配列を返します。これにより、エンジンはさまざまな形式を処理できます。それぞれの形式では、わずかな変更のみを行う必要があります。



関数は次のようになりますreturnPointsInCircle()



（JavaScriptの場合）。

 function returnPointsInCircle() { //      var pointArray = new Array(); // ,    var f = 1 - radius; //      (   ) var ddFx = 1; //  x var ddFy = -2 * this.radius; //  y var x = 0; var y = this.radius; //      , //       pointArray.push(new Point(this.centerX, this.centerY + this.radius)); pointArray.push(new Point(this.centerX, this.centerY - this.radius)); pointArray.push(new Point(this.centerX + this.radius, this.centerY)); pointArray.push(new Point(this.centerX - this.radius, this.centerY)); while(x < y) { if(f >= 0) { y--; ddFy += 2; f += ddFy; } x++; ddFx += 2; f += ddFx; //   pointArray.push(new Point(x0 + x, y0 + y)); pointArray.push(new Point(x0 - x, y0 + y)); pointArray.push(new Point(x0 + x, y0 - y)); pointArray.push(new Point(x0 - x, y0 - y)); pointArray.push(new Point(x0 + y, y0 + x)); pointArray.push(new Point(x0 - y, y0 + x)); pointArray.push(new Point(x0 + y, y0 - x)); pointArray.push(new Point(x0 - y, y0 - x)); } return pointArray; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

if



メインレンダリングサイクルにもう1つの構成を追加するだけで、これらの円はコードに完全に統合されます！



更新されたレンダリングサイクルは次のようになります。

  //     if(class type == point) { //    } else if(class type == LineSegment) { var segmentArray = LineSegment.returnPointsInSegment(); //loop through points in the array, drawing and culling them as we have previously } else if(class type == Circle) { var circleArray = Circle.returnPointsInCircle(); //     ,    ,     }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで2つの新しいクラスができたので、何かしましょう！

---

ラスタライズウィザード

今回はプログラムがシンプルになります。ユーザーがマウスボタンをクリックすると、クリックポイントを中心とし、ランダムな半径の円が描画されます。



コードを見てみましょう：

 main{ //   API //   (   ) var camera = new Camera(); //    camera.objectsInWorld[]; //   100     //    camera.minX = 0; camera.maxX = screenWidth; camera.minY = 0; camera.maxY = screenHeight; camera.minZ = 0; camera.maxZ = 100; while(key != esc) { if(mouseClick) { //   camera.objectsInWorld.push(new Circle(mouse.x,mouse.y,random(3,10)); //    camera.drawScene(); } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

すべてが成功したら、エンジンを使用して素晴らしい円を描くことができます。

---

おわりに

エンジンにラスタライズの基本機能を追加したら、ようやく画面上に有用なオブジェクトを描画し始めます！まだ複雑なことはありませんでしたが、必要に応じて、セグメントやサークルなどから人々を引き出せます。



次の部分では、ラスタライズについてもう一度見ていきます。今回だけ、さらに2つのクラスをエンジンに追加します：三角形と四角形。

パート5：三角形と四角形をラスタライズする

クラスを作成するには、Triangle



とQuad



私たちは積極的にクラスを使用しますLineSegment



。

---

三角形のラスタライズ

Triangle



エンジンでのクラスの実装は非常に簡単です。特にLineSegment



、すべてのラスタライズが行われるclassの使用のおかげです。このクラスを使用すると、3つのポイントを割り当て、それらの間に線セグメントを描画して、閉じた三角形を作成できます。



クラスのスケッチは次のようになります。

 Triangle Class { Variables: //    int Point1X, Point1Y; int Point2X, Point2Y; int Point3X, Point3Y; Function: array returnPointsInTriangle; //    }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

標準化のために、3つの点が時計回りに三角形で宣言されていると仮定します。



次に、クラスLineSegment



を使用して、次の関数を記述できますreturnPointsInTriangle()



。

 function returnPointsInTriangle() { array PointsToReturn; //       //          PointsToReturn.push(new LineSegment(this.Point1X, this.Point1Y, this.Point2X, this.Point2Y)); PointsToReturn.push(new LineSegment(this.Point2X, this.Point2Y, this.Point3X, this.Point3Y)); PointsToReturn.push(new LineSegment(this.Point3X, this.Point3Y, this.Point1X, this.Point1Y)); return(PointsToReturn); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

悪くないよね？教室LineSegment



ではすでに多くの作業を行っているため、より複雑な形状を作成するためにセグメントを順番に接続するだけです。これにより、新しいポリゴンを追加するだけでLineSegment



（そしてクラス自体により多くのポイントを格納することで）、より複雑なポリゴン（ポリゴン）を画面上に簡単に作成できます。



次に、正方形クラスを作成して、このシステムにポイントを追加する方法を見てみましょう。

---

正方形の使用

四角形コントロールクラスを実装するには、クラスにいくつかの追加を追加するだけですTriangle



。別のポイントセットを使用すると、四辺形クラスは次のようになります。

 Quad Class { Variables: int Point1X, Point1Y; //    int Point2X, Point2Y; int Point3X, Point3Y; int Point4X, Point4Y; Function: array returnPointsInQuad; //    }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次のreturnPointsInQuad



ように、関数に別のラインセグメントを追加するだけです。

 function returnPointsInQuad() { array PointsToReturn; //       //         PointsToReturn.push(new LineSegment(this.Point1X, this.Point1Y, this.Point2X, this.Point2Y)); PointsToReturn.push(new LineSegment(this.Point2X, this.Point2Y, this.Point3X, this.Point3Y)); PointsToReturn.push(new LineSegment(this.Point3X, this.Point3Y, this.Point4X, this.Point4Y)); PointsToReturn.push(new LineSegment(this.Point4X, this.Point4Y, this.Point1X, this.Point1Y)); return(PointsToReturn); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このクラスの作成方法は非常に簡単ですが、すべてのポリゴンを1つのクラスにカプセル化するはるかに簡単な方法があります。ループと配列の魔法を使用して、ほとんどあらゆる複雑な形状に対応できるポリゴンのクラスを実装できます！

---

ポリゴンを使用します

拡大し続けるポリゴンクラスを作成するには、2つの重要な手順が必要です。最初の方法は、すべてのポイントを配列に入れて、次のようなクラスのスケッチを作成することです。

 Polygon Class { Variables: array Points; //      Function: array returnPointsInPolygon; //,     }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

2つ目は、ループを使用して、関数内の不特定数のラインセグメント全体をトラバースするreturnPointsInPolygon()



ことです。これは次のようになります。

 function returnPointsInPolygon { array PointsToReturn; //      //              (  ) for(int x = 0; x < this.Points.length; x+=2) { if(   ) { //          PointsToReturn.push(new LineSegment(this.Points[x], this.Points[x+1], this.Points[x+2], this.Points[x+3])); } else if(  ) { //          PointsToReturn.push(new LineSegment(this.Points[x-2], this.Points[x-1], this.Points[0], this.Points[1])); } } //   return PointsToReturn; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このクラスをエンジンに追加すると、三角形から39面のモンスターまで、1行のコードで何でも作成できます。

---

ポリゴンクリエイター

新しいポリゴンクラスを試すために、すべての機能を示すプログラムを作成しましょう。このプログラムでは、ユーザーはキーを使用して、表示されたポリゴンの側面を追加または削除できます。もちろん、多角形の辺の数に制限を設ける必要があります。辺が3つ未満になると、多角形ではなくなります。ポリゴンの側面の上限についてはあまりよく気にしません。ただし、コードに新しいポイントを設定するため、辺の数を10に制限します。



プログラムの仕様は、次の部分に分けることができます。

• 画面上のポリゴンの初期描画。
• Aを押すと、ポリゴンの辺の数を1つ減らします。
• Sキーを押すとき、ポリゴンの辺の数を1増やします。
• 多角形の辺の数は3以上でなければなりません。
• 多角形の辺の数は10を超えてはなりません。

コードがどのように見えるかを見てみましょう。

 main{ //   API //   (   ) var camera = new Camera(); //    camera.objectsInWorld[]; //    //    camera.minX = 0; camera.maxX = screenWidth; camera.minY = 0; camera.maxY = screenHeight; camera.minZ = 0; camera.maxZ = 100; //c       var threeSides = new Array(100,100,100,50,50,50); var fourSides = new Array(points in here); var fiveSides = new Array(points in here); var sixSides = new Array(points in here); var sevenSides = new Array(points in here); var eightSides = new Array(points in here); var nineSides = new Array(points in here); var tenSides = new Array(points in here); //         var sidesArray = new Array(threeSides, fourSides, fiveSides, sixSides, sevenSides, eightSides, nineSides, tenSides); //     var polygonPoints = 3; //    var polygon = new Polygon(sidesArray[0][0], sidesArray[0][1], sidesArray[0][2], sidesArray[0][3], sidesArray[0][4], sidesArray[0][5],); //     camera.drawScene(); //     escape while(key != esc) { if(key pressed == 'a') { //        3 if(polygonPoints != 3) { //   polygonPoints--; // ,       } //  camera.drawScene(); } else if(key pressed == 's') { //        10 if(polygonPoints != 10) { //   polygonPoints++; // ,       } //  camera.drawScene(); } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

私たちの小さなプログラムでは、画面上のポリゴンを変更できるようになりました！プログラムをもう少し強力にしたい場合は、ポリゴンを変更してアルゴリズムを追加し、スケーリングを簡素化できます。存在するかどうかはわかりませんが、存在する場合は、無限にスケーラブルなポリゴンを簡単に取得できます！

---

おわりに

現在、エンジンには多くのラスタライズ操作があり、ほぼすべての必要な形状を作成できます（ただし、それらの一部は組み合わせが必要です）。次のパートでは、フォームの描画から離れて、他のプロパティについて説明します。画面に小さな色を追加することに興味がある場合は、次のパートをお読みください！

パート5：色

理論上のエンジンには、必要なものがほぼすべて含まれています：

• クラスPoint
  
  
  
  とVector
  
  
  
  （エンジンのビルディングブロック）。
• 点の変換の機能。
• クラスCamera
  
  
  
  （スコープを設定し、画面外のポイントを切り取ります）。
• ラスタライズ用の3つのクラス（線分、円、多角形）。

それでは、色を追加しましょう！

---

みんなの色！

エンジンは色を処理し、その値をクラスに保存しますPoint



。これにより、各ポイントに独自の色を持たせることができ、ライティングとシェーディングの計算が大幅に簡素化されます（少なくとも人間にとっては-そのようなエンジンコードはあまり効果的ではありません）。シーンのライティングとシェーディングを計算するとき、点のリストを使用して関数を作成し、光源までの距離を考慮してすべての点を処理し、それに応じて色を変更できます。



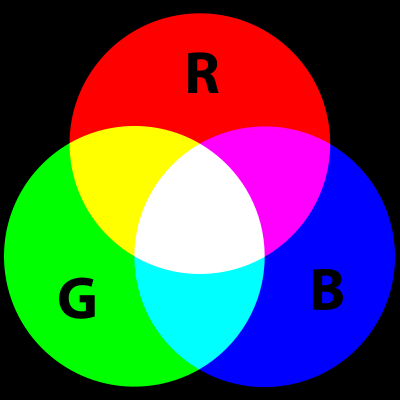
プログラミングで色を保存する最も標準的な方法の1つは、赤、緑、青の値を使用することです（通常、加法混色と呼ばれます）。各色成分の0〜255の値を保存することにより、色の大きなパレットを作成できます。 （これはほとんどのAPIが色を定義する方法であるため、互換性のためにこのメソッドを使用することは論理的です）。



使用されるグラフィックスAPIに応じて、これらの値は10進数（255,0,0



）または16進数（0xFF0000



または#FF0000



）で送信できます。 10進形式を使用します。これは、作業がはるかに簡単だからです。さらに、グラフィカルAPIが16進値を使用している場合、おそらく10進値を16進値に変換する機能があります。つまり、これは問題になりません。







カラーモデルの実装を開始するために、我々はクラスポイントで3つの新しい変数を追加しますred



、blue



とgreen



。これまでのところ、理解できないことは何も起きていませんが、クラスのスケッチは次のようになりPoint



ます。

 Point Class { Variables: num tuple[3]; //(x,y,z) num red, green, blue; //     r, g, b Operators: Point AddVectorToPoint(Vector); Point SubtractVectorFromPoint(Vector); Vector SubtractPointFromPoint(Point); Null SetPointToPoint(Point); Functions: drawPoint; //      }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ドットの色を保存するために必要なのはそれだけです。指定した色を使用するようにカメラのレンダリング関数を変更する必要があります。



関数のタイプは、使用するグラフィカルAPIに大きく依存しますが、通常、すべてのインターフェイスには同様の関数があります。

 object.setColor(red, green, blue)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

グラフィカルAPIが10進数ではなく16進数の色の値を使用する場合、関数は次のようになります。

 object.setColor(toHex(red,green,blue))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この関数はtoHex()



、RGB値を16進値に変換する関数を使用します（異なるAPIでは関数の名前は異なります）。これを手動で行う必要はありません。



これらの変更を行うことにより、シーン内に色付きのドットを取得できます。次の段階では、フォーム全体を色付けできるように、ラスタライズクラスを補完します。



この機能をクラスに追加するには、色管理をコンストラクター関数に追加するだけです。次のようになります。

 lineSegment::constructor(startX, startY, endX, endY, red, green, blue) { this.startX = startX; this.startY = startY; this.endX = endX; this.endY = endY; this.red = red; this.green = green; this.blue = blue; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、配列の各ポイントが指定された色を持つように、返されるポイントの関数を変更するだけです。新しい関数は次のようになります。

 function returnPointsInSegment() { //        var pointArray = new Array(); //          var x0 = this.startX; var y0 = this.startY; var x1 = this.endX; var y1 = this.endY; //     ,     var dx = Math.abs(x1-x0); var dy = Math.abs(y1-y0); var sx = (x0 & x1) ? 1 : -1; //  x var sy = (y0 & y1) ? 1 : -1; //  y var err = dx-dy; //    //     pointArray.push(new Point(x0,y0,this.red,this.green,this.blue)); //   while(!((x0 == x1) && (y0 == y1))) { var e2 = err * 2; //   //    ,       (  ) if(e2 => -dy) { err -= dy; x0 += sx; } if(e2 < dx) { err += dx; y0 += sy; } //     pointArray.push(new Point(x0, y0,this.red,this.green,this.blue)); } return pointArray; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、ラインセグメント上の各ポイントは、ラインセグメントに同じ色が転送されます。このメソッドを使用して、色およびその他のクラスのラスタライズを指定すると、シーンが異なる色でペイントされます！



プログラムを作成して、新しい機能を使用しましょう。

---

1670万色の実験

加法混色を使用すると、単純な表記法（r,g,b



）を使用して1670万色以上を簡単に作成できます。この膨大な量の色すべてを活用するプログラムを作成します。



ユーザーがキーストロークを押すことで赤、緑、青の色成分を個別に制御できるようにし、好きな色を選択できるようにします。



プログラムの仕様は次のとおりです。

• 画面上にオブジェクトを描画します。
• Aキーを押すと、赤のコンポーネントの値が減少し、Qを押すと増加します。
• Sキーを押すと、緑のコンポーネントの値が減少し、Wを押すと増加します。
• Dキーを押すと、青のコンポーネントの値が減少し、Eを押すと増加します。
• 色を更新した後にオブジェクトを再描画します。
• コンポーネントの値を制限し、0〜255を超えないようにする必要があります。

これらすべてを念頭に置いて、プログラムの概要がどのように見えるかを見てみましょう。

 main{ //   API //   (   ) var camera = new Camera(); //    //    camera.minX = 0; camera.maxX = screenWidth; camera.minY = 0; camera.maxY = screenHeight; camera.minZ = 0; camera.maxZ = 100; // ,      var red, green, blue; //       while(key != esc) { if(key press = 'a') { if(red > 0) { red --; object.red = red; //  } } if(key press = 'q') { if(red < 255) { red ++; object.red = red; //  } } if(key press = 's') { if(green > 0) { green --; object.green = green; //  } } if(key press = 'w') { if(green < 255) { green ++; object.green = green; //  } } if(key press = 'd') { if(blue > 0) { blue --; object.blue = blue; //  } } if(key press = 'e') { if(blue < 255) { blue ++; object.blue = blue; //  } } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、オブジェクトを試して任意の色を付けることができます！

---

おわりに

エンジンに色を追加し、照明を操作するために必要なものがすべて揃いました。次のパートでは、光源を作成するプロセスを見て、これらの光源がドットの色に影響を与えることができる関数を作成します。

パート7：動的照明

このパートでは、ダイナミックライティングの非常に基本的な部分のみを検討しますので、怖がらないでください（このトピック全体は非常に広範であり、本全体が書かれています）。



具体的には、半径が一定の単一ポイントの単一色の動的照明システムを作成します。しかし、始める前に、以前に作成した便利なクラスを見てみましょう。

---

繰り返し

画面への出力プロセスの各ポイントで、動的照明が処理されます。これは、以前の2つのクラスであるclass Point



とclass を積極的に使用することを意味しCamera



ます。それらは次のようになります。

 Point Class { Variables: num tuple[3]; //(x,y,z) Operators: Point AddVectorToPoint(Vector); Point SubtractVectorFromPoint(Vector); Vector SubtractPointFromPoint(Point); Null SetPointToPoint(Point); Functions: drawPoint; //      } Camera Class { Vars: int minX, maxX; int minY, maxY; int minZ, maxZ; array objectsInWorld; //    Functions: null drawScene(); //      }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この情報に基づいて簡単な照明クラスを作成しましょう。

---

照明クラス

動的照明の例。ソース：http : //redeyeware.zxq.net



動作するには、照明クラスにいくつかの情報、つまり位置、色、タイプ、強度（または照明の半径）が必要です。



前に述べたように、ライティングは各ポイントが描画される前に計算されます。このアプローチの利点は、エンジン構造が簡単になり、プログラムの負荷のほとんどが中央処理装置に転送されることです。照明を事前に計算しておくと、負荷はコンピューターのハードドライブに転送され、エンジンの設計によっては実装がより容易またはより困難になります。



これらすべてを念頭に置いて、クラスは次のようになります。

 Lighting Class { Variables: num position[3]; //(x,y,z) num red = 255; //,    r     num green = 255; //,    g     num blue = 255; //,    b     string lightType = "point"; //  num radius = 50; //     }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

当分の間、簡単にするために、これらの値はすべてハードコーディングされたままにしますが、照明クラスの機能を拡張したい場合は、他の関数、コンストラクターなどを使用してこれらの値を簡単に変更できます。



ただし、動的照明の重要な計算はすべてカメラクラスで実行されるため、見てみましょう。

---

光？カメラ？モーター

動的照明の別の例。ソース：http : //blog.illuminatelabs.com/2010/04/hdr-and-baked-lighting.html



次に、光源を保存するために使用するカメラクラスに新しい変数を追加します。これまでのところ、この変数にはソースのインスタンスが1つしか含まれていませんが、複数のポイントソースを格納できるように簡単に拡張できます。



点が描画される直前に、光源の半径内にあるかどうかを確認します。ある場合は、ポイントとソースの位置との間の距離を見つけて、距離に応じてポイントの色を変更する必要があります。



これらすべてを念頭に置いて、カメラ関数のコードに似たコードを追加できますdrawScene()



。

 if(currentPoint.x >= (light.x - light.radius)){ //        if(currentPoint.x <= (light.x + light.radius)){ //        if(currentPoint.y >= (light.y - light.radius)){ //        if(currentPoint.y <= (light.y + light.radius)){ //        //      (distance) //    (percentage = distance / radius) point.red += (light.red * percentage); //   ,      point.green += (light.green * percentage); //   ,      point.blue += (light.blue * percentage); //   ,      } } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ご覧のとおり、ポイントの色を変更する方法はまだ複雑ではありません（ただし、必要に応じて使用できるものは他にもたくさんあります）。光源の中心までの距離に応じて、ポイントの色をパーセンテージで変更します。この照明方法ではシェーディングがまったく考慮されていないため、光源から遠いポイントは暗くならず、オブジェクトは背後にある他のオブジェクトからの光をブロックしません。

---

光に従ってください

今回のプログラムでは、画面上のいくつかの永続的なフォームを使用します。任意の形状を選択できますが、この例ではいくつかの単純なポイントを使用します。ユーザーが画面をクリックすると、この時点で光源が作成されます。次に押すと、ポイントを新しい位置に移動します。これにより、動作中の動的な照明を観察できます。



プログラムは次のようになります。

 main{ //   API //   (   ) var camera = new Camera(); //    //    camera.minX = 0; camera.maxX = screenWidth; camera.minY = 0; camera.maxY = screenHeight; camera.minZ = 0; camera.maxZ = 100; //         while(key != esc) { if(mouseClick) { if(firstClick) { //         } else { //     } camera.drawScene(); } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ダイナミックライティングの実際の動作を理解し、ゲームエンジンにどの程度の深さが追加されるかを確認できます。

---

おわりに

ダイナミックライティングはシンプルですが、必要に応じて簡単に拡張できます。かなりシンプルだが興味深い追加：

• 可変照明半径
• 照明の変更可能な色（色を均一に変更する代わりに、特定の色の一部に変更できます）
• (, ..)