ニューラルネットワークを使用して手書きの数字を認識するパート1

こんにちは、Habr！ この一連の記事では、 Michael Nielsonの著書Neural Networks and Deep Learning の 最初の章の英語からの短い翻訳を提供します。

読みやすくするために、Habréのいくつかの記事に翻訳を分割しました。

パート1） ニューラルネットワークの概要

パート2）構築と勾配降下

パート3）数字認識のためのネットワーク実装

パート4）ディープラーニングについて

はじめに

人間の視覚システムは、世界で最も驚くべきものの1つです。 私たちの脳の各半球には、数百億の接続を持つ1億4000万個のニューロンを含む視覚皮質がありますが、この皮質は1つではなく、いくつかあり、一緒に私たちの頭の中で実際のスーパーコンピューターを形成します。私たちの世界の一部。 しかし、たとえば手書きの数字を認識するためのプログラムを作成しようとすると、視覚画像の認識の難しさが明らかになります。

単純な直感-「9ウエイトの上部にループがあり、下部に垂直尾部がある」ことをアルゴリズム的に実装するのはそれほど簡単ではありません。 ニューラルネットワークは例を使用して、いくつかのルールを導き出し、それらから学習します。 さらに、ネットワークを示す例が多いほど、手書きの数字について学習するので、より正確に分類されます。 99行以上の精度で手書きの数字を決定するプログラムを74行のコードで記述します。 さあ、行こう！

パーセプトロン

ニューラルネットワークとは まず、人工ニューロンのモデルについて説明します。 パーセプトロンは1950年にフランクローゼンブラットによって開発されました。今日は、その主要モデルの1つであるS字パーセプトロンを使用します。 それでは、どのように機能しますか？ Persepronは入力ベクトルを受け入れます $$$\ bar {x} = \左\ {x_ {1}、x_ {2}、x_ {3}、...、x_ {N} \右\}、x_ {i} \ in \ mathbb {R}$ そして、いくつかの出力値を返します $$$出力\ in \ mathbb {R}$ 。

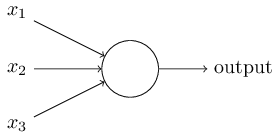
Rosenblattは、出力値を計算するための簡単なルールを提案しました。 彼は「重要性」の概念を導入し、次に各入力値の「重み」を導入しました $$$\ bar {w} = \左\ {w_ {1}、w_ {2}、w_ {3}、...、w_ {N} \右\}、w_ {i} \ in \ mathbb {R}$ 。 私たちの場合 $$$出力$ かどうかに依存します $$$\ sum_ {i = 1} ^ {N} x_ {i} w_ {i}$ 特定のしきい値より大きいまたは小さい $$$しきい値\ in \ mathbb {R}$ 。

$$

$$output = \ begin {cases} 0＆\ text {if} \ sum_ {i = 1} ^ {N} x_ {i} w_ {i} \ leq threshold \\ 1＆\ text {if} \ sum_ {i = 1} ^ {N} x_ {i} w_ {i}>しきい値\ end {cases}$$

そして、それは私たちが必要とするすべてです！ 変化する $$$しきい値$ および重みベクトル $$$\バー{w}$ 、まったく異なる意思決定モデルを取得できます。 ニューラルネットワークに戻ります。

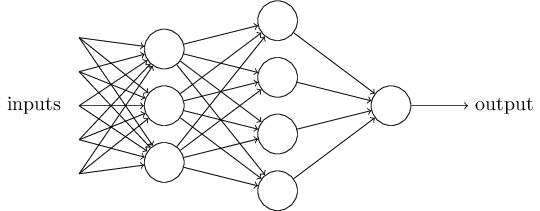
したがって、ネットワークはいくつかのニューロン層で構成されていることがわかります。 最初の層は、入力層または受容体（ $$$受容体、InputLayer$ ）、次のレイヤーが非表示（ $$$HiddenLayer$ ）、最後は出力層（ $$$OutputLayer$ ） 状態 $$$\ sum_ {i = 1} ^ {N} x_ {i} w_ {i}>しきい値$ かなりかさばりましょう $$$\ sum_ {i = 1} ^ {N} x_ {i} w_ {i}$ ベクトルのスカラー積 $$$\ bar {x} \ cdot \ bar {w}$ 。 次に置く $$$b = -threshold$ 、パーセプトロン変位と呼ぶか、 $$$バイアス$ そして転送 $$$b$ 左側に。 取得するもの：

$$

$$output = \ begin {cases} 0＆\ text {if} \ bar {x} \ cdot \ bar {w} + b \ leq 0 \\ 1＆\ text {if} \ bar {x} \ cdot \ bar {w} + b> 0 \ end {cases}$$

学習問題

トレーニングがどのように機能するかを調べるために、ネットワークの重みまたはバイアスを少し変更したと仮定します。 この重みの小さな変化が、ネットワークからの出力に対応する小さな変化を引き起こすことを望みます。 概略的には、次のようになります。

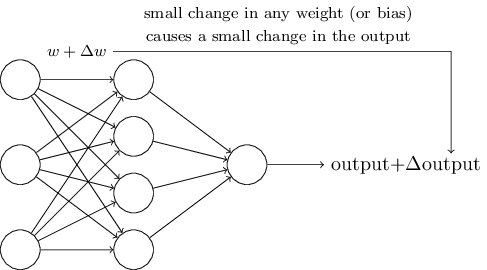
これが可能である場合、重みを有利に操作してネットワークを徐々に訓練することができますが、問題は特定のニューロンの重みの変更により、その出力が0から1に完全に「反転」する可能性があることです。ネットワーク全体の大きな予測エラーになりますが、この問題を回避する方法があります。

シグモイドニューロン

シグモイドニューロンと呼ばれる新しいタイプの人工ニューロンを導入することにより、この問題を克服できます。 シグモイドニューロンはパーセプトロンに似ていますが、重みと変位の小さな変化が出力の小さな変化のみを引き起こすように修正されています。 シグモイドニューロンの構造は似ていますが、今では入力を受け取ることができます $$$0 \ leq x_ {i} \ leq 1、\ forall x_ {i} \ in \ bar {x}$ 、および出力 $$$\ sigma（\ bar {x} \ cdot \ bar {w} + b）$ どこで

$$

$$\ begin {eqnarray} \ sigma（z）= \ frac {1} {1 + e ^ {-z}}。 \ end {eqnarray}$$

まったく異なるケースのように思えますが、パーセプトロンとS字型ニューロンには多くの共通点があることを保証します。 と仮定する $$$z = \ bar {x} \ cdot \ bar {w} + b \右矢印\ infty$ それから $$$e ^ {-z} \右矢印0$ したがって、 $$$\シグマ（z）\右矢印1$ 。 逆の場合も当てはまります $$$z = \ bar {x} \ cdot \ bar {w} + b \右矢印-\ infty$ それから $$$e ^ {-z} \右矢印\ infty$ そして $$$\シグマ（z）\右矢印0$ 。 明らかに、シグモイドニューロンを使用すると、パーセプトロンがより滑らかになります。 そして本当に：

$$

$$\デルタ出力\約\ sum_ {i = 1} ^ {N} \ frac {\ partial output} {\ partial w_ {i}} \ Delta w_ {i} + \ frac {\ partial output} {\ partial b } \デルタb$$

ニューラルネットワークアーキテクチャ

ニューラルネットワークの入力層と出力層の設計は、非常に簡単な作業です。 たとえば、手書きの「9」が画像内にあるかどうかを判断しようとしているとします。 ネットワークを設計する自然な方法は、入力ニューロンの画像ピクセルの強度をエンコードすることです。 画像にサイズがある場合 $$$64 \ cdot 64$ その後、私たちは持っています $$$4,096 = 64 \ cdot 64$ 入力ニューロン。 出力層には1つのニューロンがあり、0.5より大きい場合は出力値を含み、それ以外の場合は画像「9」上にあります。 入力層と出力層の設計は非常に簡単な作業ですが、隠れ層のアーキテクチャを選択するのは芸術です。 研究者は、隠れ層の数とネットワークトレーニング時間の補償に役立つような、多くの隠れ層設計のヒューリスティックを開発しました。

これまで、1つの層からの出力が次の層の信号として使用されるニューラルネットワークを使用していました。このようなネットワークは、直接ニューラルネットワークまたは直接分布ネットワーク（ $$$FeedForward$ ） ただし、フィードバックループが可能なニューラルネットワークの他のモデルがあります。 これらのモデルは、 リカレントニューラルネットワーク （ $$$リカレントニューラルネットワーク$ ） 再帰的なニューラルネットワークは、直接接続されたネットワークよりも影響力が小さくなりました。これは、リカレントネットワークの学習アルゴリズム（少なくとも現在まで）の効率が低いためです。 しかし、リカレントネットワークは依然として非常に興味深いものです。 彼らは、直接接続されたネットワークよりも、私たちの脳がどのように機能するかに精神的にずっと近いです。 また、リピートネットワークは、直接アクセスネットワークを使用すると非常に困難に解決できる重要な問題を解決できる可能性があります。

ですから、今日のすべてについて、次の記事で降下の勾配と将来のネットワークのトレーニングについてお話します。 ご清聴ありがとうございました！