🌵 👩🏻‍🔧 🍬 レベル固定法（レベルセット法）によるバイナリ画像のセグメンテーション 🔩 ⬛️ 💶

画像のセグメンテーションは、デジタル画像を1つ以上の関心領域に分割するタスクです。これはコンピュータービジョンの分野における基本的な問題であり、多くの異なる方法で解決されますが、それぞれに長所と短所があります。

この記事では、レベル固定法と暗黙的に定義された動的表面の概念（レベルセット法）を簡単に確認します。また、ラベル付き距離マップであるSDT（符号付き距離変換）などの数学的構造の導入と定義を使用して、バイナリセグメンテーションにおけるこの方法の役割を検討します。

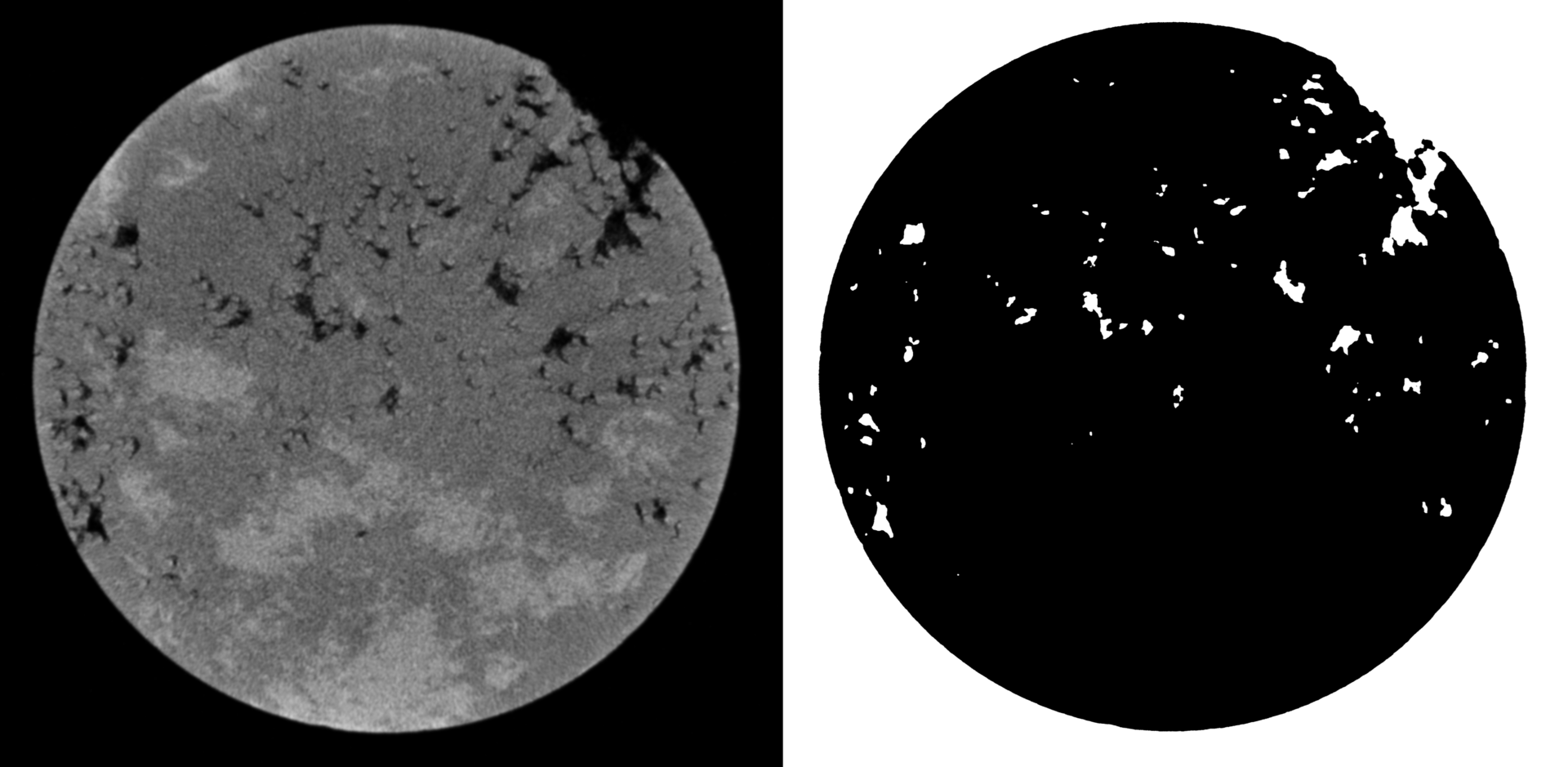
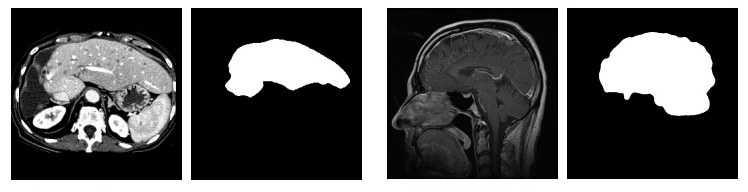左側-元の画像、右側-セグメント化

なんでこんなこと？

さまざまな業界では、多くの場合、セグメント化された画像が必要です。たとえば、医学では、さらなる分析のために臓器のデジタル3Dモデルを取得することに関心があります。セグメンテーションは、顔認識、マシンビジョンなどでも使用されます。

画像のセグメンテーションは、いくつかの理由で特に難しいタスクです。第一に、現在、普遍的なセグメンテーションアルゴリズムがないため、特定の条件に基づいてユーザーがパラメーターを選択する特別なアルゴリズムを作成する必要があります。第二に、ノイズ、不均一性などの画像の歪みは、ユーザーの介入なしにセグメンテーションアルゴリズムで考慮することは非常に困難です。

2番目の問題は通常、さまざまなフィルターで解決されます。ここでは、この技術について詳しく説明します。

石油およびガス業界での画像セグメンテーションの課題に直面しました。最初は、フラットなコアイメージがありました（上の写真のように）。セグメント化された画像を受け取ったら、境界線を補間できます。すべての画像に対してこの操作を実行すると、岩石サンプルの数学的モデルを取得できます。これを使用して、たとえば流体の流れを設定できます（モデルを連続体力学のモデルと見なす場合）。

レベル固定法

この方法は、1980年代にアメリカの数学者Stanley OscherとJames Setyanによって導入されました。コンピュータグラフィックス、画像処理、計算幾何学、最適化、計算流体力学、計算生物物理学など、多くの分野で人気があります。

レベル固定法は、レベル固定関数と呼ばれるより高次元の関数を使用して、輪郭（2次元）または表面（3次元）を暗黙的に変換します。

φ （ x 、 t ）

$φ（x、t）$ 。変換された輪郭または表面は、曲線として取得できます。

\ガンマ（x、t）= \ {φ（x、t）= 0 \}

$\ガンマ（x、t）= \ {φ（x、t）= 0 \}$ 。

この方法を使用する利点は、下図に示すように、輪郭またはサーフェスのマージや分離などのトポロジの変更が暗黙的に解決されることです。

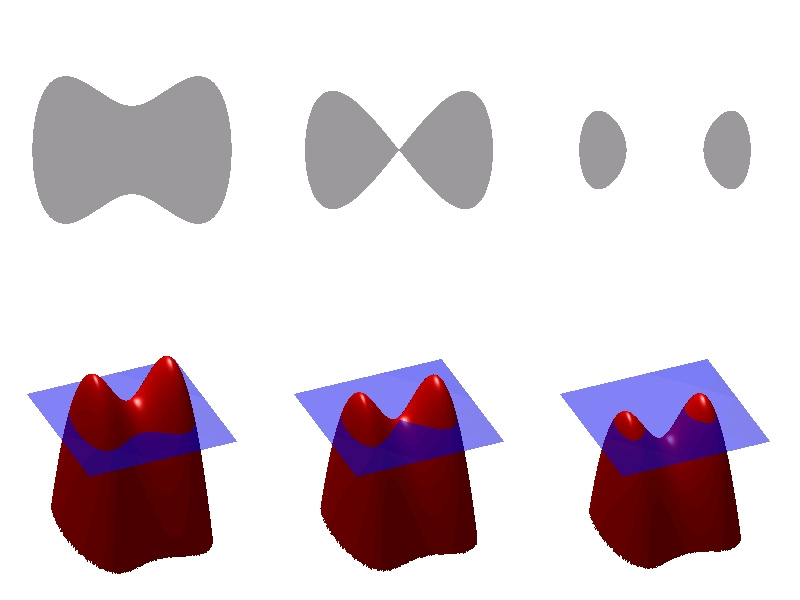
レベルロック機能（下）とパス（上）の関係を確認できます。 表面を変更すると輪郭が崩れることがわかります。

レベル修正式

輪郭または表面の定義は、レベル修正式によって決定されます。更新することにより、この偏微分方程式の数値解を取得します

φ

$φ$ 各タイムレイヤー。レベル修正方程式の一般的な形式は次の形式です。

$$表示$$ \ frac {∂φ} {∂t} = -F |∇φ| \ qquad（1）$$表示$$

ここで：

| ・ |

$|・|$ -ユークリッド標準、

φ

$φ$ -レベル固定機能、

t

$t$ -時間

F

$F$ -速度係数。

この偏微分方程式は双曲線に非常に似ています。しかし、方程式の右側には、空間微分に加えて、厳密には時間微分もありますが、厳密にはそうではありません。

ベクトルの形の特定のタスクで

F

$F$ パラメータに対して正確な場合、レベル線を異なる領域または形状に向けることができます。

セグメンテーションのアプリケーションについては、設定します

F

$F$ このように：

$$表示$$ F =αD（I）+（1-α）∇\ cdot \ frac {∇φ} {|∇φ|} \ qquad（2）$$表示$$

ここで：

D （ I ）

$D（I）$ -希望するセグメンテーションに決定を下すデータ機能、

I

$I$ -ピクセル強度の値、

$ inline $∇\ cdot \ frac {∇φ} {|∇φ|} $ inline $ -関数の曲率の中間項

φ

$φ$ この機能をスムーズに保ちますが、

a l p h a

$\ alpha$ -重量パラメータ。

データ機能

D （ I ）

$D（I）$ セグメンテーションを推進する主な「力」として機能します。することによって

D

$D$ 望ましい領域ではプラス、望ましくない領域ではマイナスの場合、モデルは望ましいセグメンテーションに努めます。簡単なデータ関数を次に示します。

D （ I ） = ε - | I - T | q q u a d （ 3 ）

$D（I）=ε-| I-T | \ qquad（3）$

彼女の作品を以下の図に示します。

つまり、ピクセル値が間隔に収まる場合

（ T - ε 、 T + ε ）

$（T-ε、T +ε）$ 、それからモデルの範囲は拡大します、さもなければそれは狭くなります。

したがって、セグメンテーションに指定する必要がある3つのユーザーパラメーターは次のとおりです。

T 、

$T、$ εおよび

a l p h a

$\ alpha$ 。

たとえば、画像上で明るさの低いオブジェクト（黒い領域）を選択する必要がある場合、

T

$T$ ゼロに等しい値が選択されます。

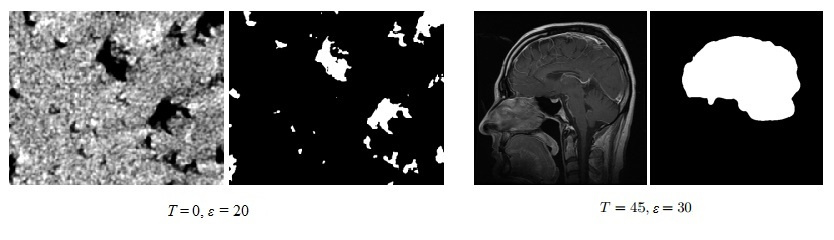
左側で、黒い領域を選択し、右側で、目的の領域の輝度を高くします。

$T = 45$

初期マスクも必要です。

m

$m$ 。最初の近似は、どちらを選択するかによって異なります。

φ

$φ$ 。これを行うために、 マーク付き距離マップの概念を導入します

マーク付き距離変換

距離マップは、画像と同じ次元のマトリックスです。このように構築されます。画像の各ピクセルに対して、このピクセルからオブジェクトの境界にある最も近いピクセルまでの最小距離に等しい値が計算されます。距離関数の数学的定義

d ： R^{3} \か ら R

$d：R ^ 3 \からR$ セットSの場合：

d （ r 、 S ） = m i n | r - S | q q u a d f o r a l l q q u a d r \in R^{3}

$d（r、S）= min | r-S | \ qquad for all \ qquadr∈R^ 3$

ラベル付き距離マップは、オブジェクトの外側にあるピクセル値の前に正の符号を持ち、内部にあるピクセル値に対しては負の符号を持つマトリックスです。これは、実装中に実装されるサイン協定ですが、サインの反対の規則を使用できます。セル値は選択したメトリックに依存することに注意してください：いくつかの一般的な距離メトリックは、ユークリッド距離、チェビシェフ距離、チェス盤距離、および都市ブロック距離（タクシージオメトリ、都市ブロック距離、マンハッタン距離）です。

左側は最初のマスクです。 これは、関心のあるオブジェクト内にある任意の形状のオブジェクトです。 ほとんどの場合、これは長方形です。設定が非常に簡単だからです。 一定回数の反復の後、右側の関数（レベル変更関数）が変化し、ゼロ平面との交点が対象の曲線を提供します

離散化

式（1）のレベル式は、逐次計算または並列計算のために離散化する必要があります。これは、フロー（アップウィンド）に対する違いを持つ差分スキームを使用して行われます。

方程式（1）の時間離散化の1次精度法は、直接オイラー法によって指定されます。

$$表示$$ \ frac {（φ^ {t + ∆t}-φ^ t）} {∆t} + F ^ t \cdot∇φ^ t = 0 \ qquad（4）$$表示$$

ここで：

φ^{t}

$φ^ t$ -現在の値

φ

$φ$ 時間に

t

$t$

F^{t}

$F ^ t$ 時間の速度ベクトルです

t

$t$

\nabla φ^{t}

$∇φ^ t$ -勾配値

φ

$φ$ 時間に

t

$t$

勾配を計算するとき、空間微分に関して細心の注意を払わなければなりません

φ

$φ$ 。これは、式（4）の拡張形式を考慮する場合に最もよく見られます。

$$表示$$ \ frac {（φ^ {t +Δt}-φ^ t）} {Δt} + u ^ tφ_x^ t + v ^ tφ_y^ t + w ^ tφ_z^ t = 0 \ qquad（5）$$表示$$

どこで

u 、 v 、 w

$u、v、w$ -コンポーネント

x 、 y 、 z

$x、y、z$ から

F

$F$ 。簡単にするために、特定のグリッド点で方程式（5）の一次元形式を考えます

x_{i}

$x_i$ ：

$$表示$$ \ frac {（φ^ {t + ∆t}-φ^ t）} {∆t} + u_i ^ t \ cdot（φ_x）_i ^ t = 0 \ qquad（6）$$表示$$

どこで

（ φ_{x} ）_{i}^{t}

$（φ_x）_i ^ t$ -デリバティブ

φ

$φ$ ある地点での空間で

x_{i}

$x_i$ 。どの差分スキームを使用するか、直接または逆を理解するために、符号に基づいて行います

u_{i}

$u_i$ その時点で

x_{i}

$x_i$ 。もし

u_{i} > 0

$u_i> 0$ 、値

φ

$φ$ 左から右に移動するため、逆差分スキーム（

D_{x}^{-}

$D_x ^-$ 式7）で。それどころか、

u_{i} < 0

$u_i <0$ 、その後、近づく

φ_{x}

$φ_x$ 直接差分スキームを使用する必要があります（

D_{x}^{+}

$D_x ^ +$ 式7）で。これは、導関数の近似を選択するこのプロセスです

φ

$φ$ サインベースのスペース

u_{i}

$u_i$ はフロー計算として知られています。

計算の2次元の場合

φ

$φ$ 以下に説明する導関数が必要です。画像が等方性であるという仮定を立てることに言及する価値があります。

$$ display $$ \ begin {matrix} D_x = \ frac {φ_{i + 1、j}-φ_{i-1、j}} 2 \ qquad D_x ^ + = \ frac {φ_{i + 1、j }-φ_{i、j}} 2 \ qquad D_x ^-= \ frac {φ_{i、j}-φ_{i-1、j}} 2 \\ D_y = \ frac {φ_{i、j + 1 }-φ_{i、j-1}} 2 \ qquad D_y ^ + = \ frac {φ_{i、j + 1}-φ_{i、j}} 2 \ qquad D_y ^-= \ frac {φ_{i 、j}-φ_{i、j-1}} 2 \ end {matrix} \ qquad（7）$$ display $$

\nabla φ

$∇φ$ 風上スキームを使用して近似：

\nabla φ_{m a x} = b e g i n b m a t r i x s q r t m a x （ D_{x}^{+} 、 0 ）^{2} + m a x （ - D_{x}^{-} 、 0 ）^{2} s q r t m a x （ D_{y}^{+} 、 0 ）^{2} + m a x （ - D_{y}^{-} 、 0 ）^{2} e n d b m a t r i x q q u a d （ 8 ）

$∇φ_{max} = \ begin {bmatrix} \ sqrt {max（D_x ^ +、0）^ 2 + max（-D_x ^-、0）^ 2} \\ \ sqrt {max（D_y ^ +、0 ）^ 2 + max（-D_y ^-、0）^ 2} \ end {bmatrix} \ qquad（8）$

\nabla φ_{m i n} = b e g i n b m a t r i x s q r t m i n （ D_{x}^{+} 、 0 ）^{2} + m i n （ - D_{x}^{-} 、 0 ）^{2} s q r t m i n （ D_{y}^{+} 、 0 ）^{2} + m i n （ - D_{y}^{-} 、 0 ）^{2} e n d b m a t r i x q q u a d （ 9 ）

$∇φ_{min} = \ begin {bmatrix} \ sqrt {min（D_x ^ +、0）^ 2 + min（-D_x ^-、0）^ 2} \\ \ sqrt {min（D_y ^ +、0 ）^ 2 + min（-D_y ^-、0）^ 2} \ end {bmatrix} \ qquad（9）$

最後に、

F_{i 、 j 、 k} > 0

$F_ {i、j、k}> 0$ または

F_{i 、 j 、 k} < 0

$F_ {i、j、k} <0$ 、

\nabla φ

$∇φ$ のように思える：

$$ display $$∇φ= \ begin {cases}‖∇φ_{max}‖_2＆\ quad \ text {if} F_ {i、j、k}> 0 \\‖∇φ_{min}‖_2＆ \ quad \ text {if} F_ {i、j、k} <0 \\ \ end {cases} \ qquad（10）$$ display $$

$$表示$$φ（t +Δt）=φ（t）+ΔtF|∇φ| \ qquad（11）$$表示$$

前述のように、速度係数Fはピクセル強度と曲率値に基づいています。

曲率

以下の導関数を使用して確立された現在のレベルの値に基づいて計算します。二次元のみ

D_{x}^{+ y} 、 D_{x}^{- y} 、 D_{y}^{+ x} 、 D_{y}^{- x}

$D_x ^ {+ y}、D_x ^ {-y}、D_y ^ {+ x}、D_y ^ {-x}$ 、以前に定義された導関数とともに：

$$ display $$ \ begin {matrix} D_x ^ {+ y} = \ frac {（φ_{i + 1、j + 1}-φ_{i-1、j + 1}）} 2 \ qquad D_x ^ { -y} = \ frac {（φ_{i + 1、j-1}-φ_{i-1、j-1}）} 2 \\ D_y ^ {+ x} = \ frac {（φ_{i + 1 、j + 1}-φ_{i + 1、j-1}）} 2 \ qquad D_y ^ {-x} = \ frac {（φ_{i-1、j + 1}-φ_{i-1、j -1}）} 2 \ end {matrix} \ qquad（12）$$ display $$

法線の差を使用して、曲率は2つの法線を持つ上記の導関数を使用して計算されます

n^{+}

$n ^ +$ そして

n^{-}

$n ^-$ 。

n^{+} = b e g i n b m a t r i x f r a c D_{x}^{+} s q r t （ D_{x}^{+} ）^{2} + （ f r a c D_{y}^{+ x} + D_{y} 2 ）^{2} f r a c D_{y}^{+} s q r t （ D_{y}^{+} ）^{2} + （ f r a c D_{x}^{+ y} + D_{x} 2 ）^{2} e n d b m a t r i x q q u a d （ 13 ）

$n ^ + = \ begin {bmatrix} \ frac {D_x ^ +} {\ sqrt {（D_x ^ +）^ 2 +（\ frac {D_y ^ {+ x} + D_y} {2}）^ 2}} \\ \ frac {D_y ^ +} {\ sqrt {（D_y ^ +）^ 2 +（\ frac {D_x ^ {+ y} + D_x} {2}）^ 2}} \\ \ end {bmatrix} \ qquad（13）$

n^{-} = b e g i n b m a t r i x f r a c D_{x}^{-} s q r t （ D_{x}^{-} ）^{2} + （ f r a c D_{y}^{- x} + D_{y} 2 ）^{2} f r a c D_{y}^{-} s q r t （ D_{y}^{-} ）^{2} + （ f r a c D_{x}^{- y} + D_{x} 2 ）^{2} e n d b m a t r i x q q u a d （ 14 ）

$n ^-= \ begin {bmatrix} \ frac {D_x ^-} {\ sqrt {（D_x ^-）^ 2 +（\ frac {D_y ^ {-x} + D_y} {2}）^ 2}} \\ \ frac {D_y ^-} {\ sqrt {（D_y ^-）^ 2 +（\ frac {D_x ^ {-y} + D_x} {2}）^ 2}} \\ \ end {bmatrix} \ qquad（14）$

以下に示すように、2つの法線を使用して発散を計算し、平均曲率を計算します。

$$表示$$ H = \ frac {1} {2}∇\ cdot \ frac {∇φ} {|∇φ|} = \ frac {1} {2}（（n_x ^ +-n_x ^-）+ （n_y ^ +-n_y ^-））\ qquad（15）$$表示$$

持続可能性

安定性は、Courant-Friedrichs-Levy（CFL）条件から生じます。CFL条件では、計算回路の情報の速度は、時間とともに

∆ t

$∆t$ 1つのセルを超えない、つまり

f r a c ∆ x ∆ t > | u |

$\ frac {∆x} {∆t}> | u |$ 。私たちが持っています：

∆ t < f r a c Δ x m a x | u | q q u a d （ 16 ）

$∆t <\ frac {Δx} {max {| u |}} \ qquad（16）$

順次実装

このバイナリセグメンテーションアルゴリズムをMatlabシステムに実装します。 Matlabはテーブルの操作で素晴らしい仕事をしているので、まず、明確にするためにこれを行います。また、画像を読み取ってアルゴリズムを画面に表示できる非常に簡単な機能もあります。これにより、コードは簡潔で理解しやすくなります。 当然、たとえばCでの実装は、速度の点ではるかに有益です。 しかし、この記事では、速度を追いかけるのではなく、方法を理解しようとしています。

以下のアルゴリズムの擬似コードを見ることができます：

入力：元の画像I。ソースマスクm; しきい値T; エラーε; 反復回数N; 距離マップITSを再計算する反復回数を示す数値。
出力：セグメンテーション結果-セグメント画像。

符号付きユークリッド距離変換（SEDT）とマスクmを使用して、φ_0を初期化します。

D（I）=ε-| IT |を計算します。
1からNまでのサイクルi
- 一次微分の計算
- 二次導関数を計算する
- 通常の値を計算します $n ^ +$ そして $n ^-$
- 勾配の値を計算する $∇φ$
- 関数の値を計算します $インライン$ F =αD（I）+（1-α）∇\ cdot \ frac {∇φ} {|∇φ|} $インライン$
- レベル更新機能 $インライン$φ（t +Δt）=φ（t）+Δt\ cdot F \ cdot |∇φ| $ inline $
- i % ITS == 0
  
  場合
  
  再初期化 $φ$ SEDTを使用する
  
  終了する場合
サイクルの終わり

まず、使用する画像形式を選択します。 PGM形式は非常に便利であることがわかりました。これは、グレースケール圧縮なしでビットマップビットマップイメージを格納するためのオープン形式です。単純なASCIIヘッダーがあり、画像自体は一連のシングルバイト（0〜255のグレースケール）の符号なし整数です。このフォーマットの詳細については、標準自体で直接読むことができます。リンクはソースセクションにあります。

レベルセットの初期化コードと更新コードを分離するために、コードを「ランチャー」と「カーネル」の2つの部分に分割します。最初のファイルはダウンロードを処理し、「imread」および「imresize」機能を使用して画像の解像度を下げます。ユーザーがしきい値のパラメーターを設定

T

$T$ 、範囲

ε

$ε$ および重み付けの曲率

a l p h a

$\ alpha$ 、ランチャーを起動してから、初期マスクを形成する閉じたポリゴンの描画に進みます（基本的なインタラクティブ機能を提供します）。

そのため、画像を読み取り、すぐにゼロ行列を作成します

m

$m$ これがマスクになります：

 I = imread('test_output.pgm'); I = imresize(I, 1); init_mask = zeros(size(I,1),size(I,2));

マスクを作成するには、中心の座標とそれからの偏差を選択すると便利です。単位で満たされた長方形を取得します。コアに転送します。

 x = 400; y = 800; %   dx = 10; dy = 10; init_mask(y - dy : y + dy, x - dx : x + dx) = 1; %  seg = simpleseg(I, init_mask, max_its, E, T); %

次に、コードの中核であるsimpleseg

関数について考えます。最初に、 init_mask

マスクからSDFを取得する必要があります。

 phi = mask2phi(init_mask); % SDF function phi = mask2phi(init_a) %  SDF phi=bwdist(init_a)-bwdist(1-init_a);

曲率を計算する関数を書きましょう：

 %  function curvature = get_curvature(phi) dx = (shiftR(phi)-shiftL(phi))/2; dy = (shiftU(phi)-shiftD(phi))/2; dxplus = shiftR(phi)-phi; dyplus = shiftU(phi)-phi; dxminus = phi-shiftL(phi); dyminus = phi-shiftD(phi); dxplusy = (shiftU(shiftR(phi))-shiftU(shiftL(phi)))/2; dxminusy = (shiftD(shiftR(phi))-shiftD(shiftL(phi)))/2; dyplusx = (shiftR(shiftU(phi))-shiftR(shiftD(phi)))/2; dyminusx = (shiftL(shiftU(phi))-shiftL(shiftD(phi)))/2; nplusx = dxplus./sqrt(eps+(dxplus.^2 )+((dyplusx+dy )/2).^2); nplusy = dyplus./sqrt(eps+(dyplus.^2 )+((dxplusy+dx )/2).^2); nminusx= dxminus./sqrt(eps+(dxminus.^2)+((dyminusx+dy)/2).^2); nminusy= dyminus./sqrt(eps+(dyminus.^2)+((dxminusy+dx)/2).^2); curvature = ((nplusx-nminusx)+(nplusy-nminusy))/2;

デリバティブは、シフトされた関数行列を減算することにより計算されます

φ

$φ$ 。導関数は要素ごとに計算されないことに注意してください。これは効率が悪いためです。

 %--       function shift = shiftD(M) shift = shiftR(M')'; function shift = shiftL(M) shift = [ M(:,2:size(M,2)) M(:,size(M,2))]; function shift = shiftR(M) shift = [M(:,1) M(:,1:size(M,2)-1)]; function shift = shiftU(M) shift = shiftL(M')';

今、速度係数を考えます

F

$F$

  alpha=0.5; D = E - abs(I - T); K = get_curvature(phi); F = alpha*single(D) + (1-alpha)*K;

レベルの更新に進んだ後。これを行うには、最初に勾配を計算して安定性を維持します。

 dxplus = shiftR(phi)-phi; dyplus = shiftU(phi)-phi; dxminus = phi-shiftL(phi); dyminus = phi-shiftD(phi); gradphimax_x = sqrt(max(dxplus,0).^2+max(-dxminus,0).^2); gradphimin_x = sqrt(min(dxplus,0).^2+min(-dxminus,0).^2); gradphimax_y = sqrt(max(dyplus,0).^2+max(-dyminus,0).^2); gradphimin_y = sqrt(min(dyplus,0).^2+min(-dyminus,0).^2); gradphimax = sqrt((gradphimax_x.^2)+(gradphimax_y.^2)); gradphimin = sqrt((gradphimin_x.^2)+(gradphimin_y.^2)); gradphi = (F>0).*(gradphimax) + (F<0).*(gradphimin); dt = .5/max(max(max(abs(F.*gradphi))));

レベルのセットの機能を変更します

φ

$φ$ ：

 phi = phi + dt.*(F).*gradphi;

20回の反復ごとに中間結果を画面に表示します。

  if(mod(its,20) == 0) showcontour(I,phi,its); subplot(2,2,4); surf(phi); shading flat; end

showcontour

関数の使用：

 function showcontour(I, phi, i) subplot(2, 2, 3); title('Evolution') ; imshow (I); hold on; contour(phi, [0 0],'g','LineWidth', 2); hold off ; title([num2str(i) 'Iterations'] ); drawnow;

結果

医療と岩石の 2種類の画像でアルゴリズムテストを実施しました（この問題は卒業証書で解決したため）。

医用画像の場合、次のように機能します。

アルゴリズムがこのタスクの非常に良い仕事をしていることがわかります。

このアルゴリズムは、3次元の場合に実装できると言う価値があります。 この記事では、フィーチャーをペイントしませんが、どのように機能するかを示します。

この場合、初期マスクは立方体です（一般的な場合、もちろんこれは任意の3次元のボディです）

岩石画像のセグメンテーションでは、主にノイズの問題に直面しています。これは多くの理由による：断層撮影の誤差から逆ラドン変換の誤差まで（これはそのような画像が得られる方法です）。そのため、最初に画像をフィルタリングする必要があります。ペロンとマリックの異方性拡散のフィルターはこれで非常にうまく機能します。このフィルターに関する記事へのリンクは、既に記事の冒頭にありました。投稿の最後に彼女を置き去りにします。

ノイズの多い画像をセグメント化すると、次のようになります。

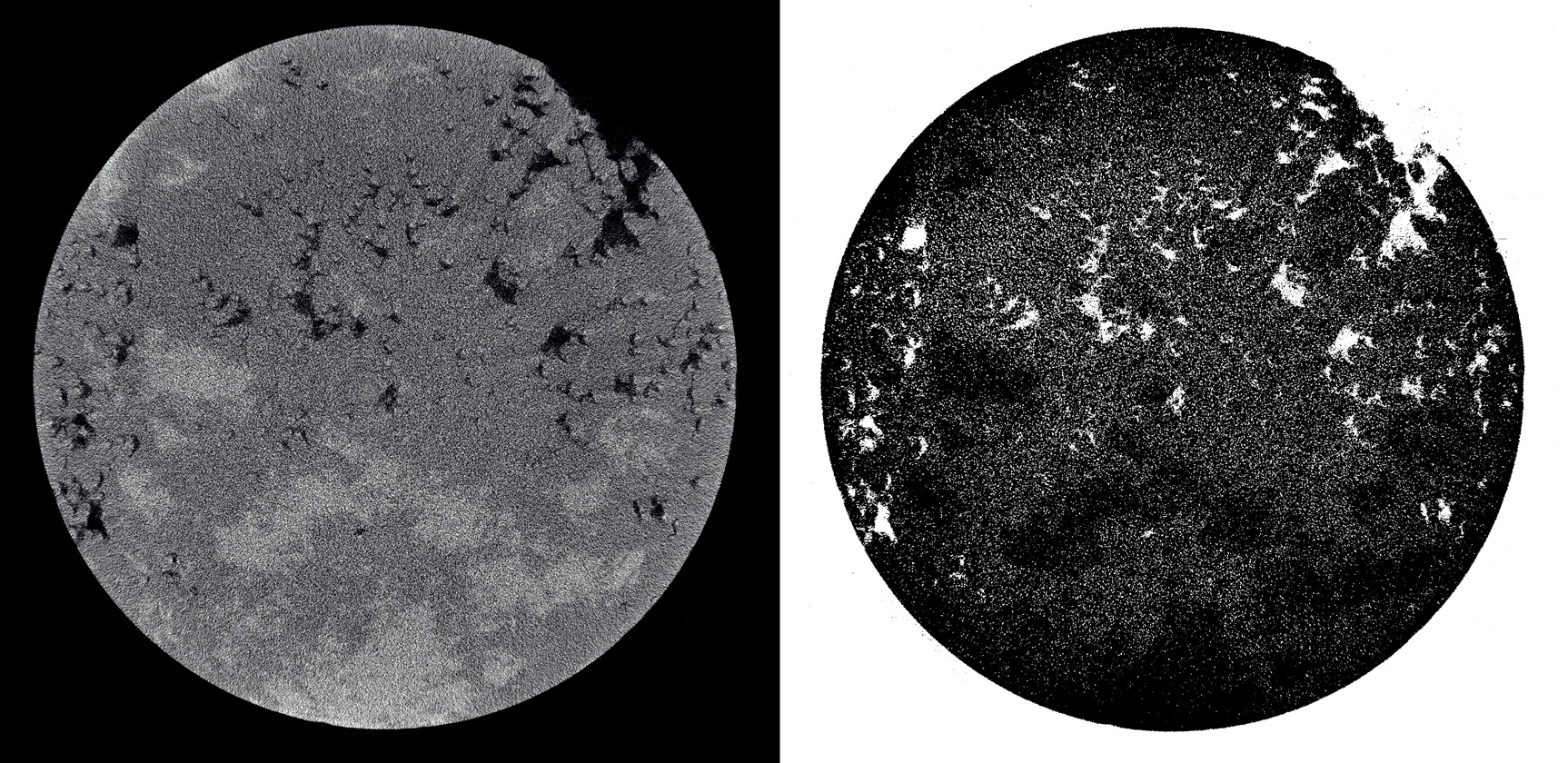
しかし、フィルターされた画像はどうですか：

結論とさらなる研究

レベル固定法は、バイナリセグメンテーションを実行するための優れた方法です。その主な欠点は、計算の複雑さが大きいことです。 Matlabが私のマシンで512x512の画像を処理するのにかかった時間（5000回の繰り返しに費やされた時間）は2737.84秒（45分）です。もちろん、これは非常に多くあります。

ただし、この事実を読んだ後に記事を閉じないでください。このアルゴリズムを選んだ主な理由は、並列性が非常に高いことです。 CUDAでこれを行いました。他の何かを使用して、たとえばコメントにそれを書くことができます。もし興味があるなら、将来、このアルゴリズムの並列化のトピックに関する次の記事を書きます。

PSソースコードへのリンクは次のとおりです。開始ファイルとセグメンテーションに直接関与する関数です。

レベル固定法（レベルセット法）によるバイナリ画像のセグメンテーション

なんでこんなこと？

レベル固定法

レベル修正式

マーク付き距離変換

離散化

曲率

持続可能性

順次実装

結果

結論とさらなる研究

ソース

More articles: