定常増分を持つ 2つのストックを取得し、それらの線形結合(スプレッド)が定常であるとわかる場合 、この時系列は共積分と呼ばれます。 共同統合の存在は、株式をヘッジし、市場に中立な戦略を構築する機会を与えてくれます。 なぜこれが可能ですか?
利益創出の基礎となる原則
時系列で見た株の価格は非常に大きく変動する可能性があることは誰もが知っています。 いずれかの論文でポジションを作成すると、そのボラティリティに関連するすべてのリスクを負うため、ほとんどの場合、非常にリスクの高いゲームになります。 ただし、このような一連のアクションは、ペアになっているため、互いに離れすぎないことが予想されます。 この概念は、長期動的平衡と呼ばれます。
定常性の文脈では、長期の動的平衡はより正確な形を取ります。 2つの統合された論文の間に構築されたスプレッドの静止列をとると、平均に戻る特性を持ちます。つまり、何らかの平衡から逸脱すると、戻ってくる傾向があります。 この原則に基づいて、市場に中立な戦略が構築されます。
株式市場で長期の動的均衡に関連するペアを見つける方法は?
相関関係
最初に思い浮かぶのは、2つの論文とトレードペア間の相関を強い相関で計算することです。 このアプローチは2つの理由で失敗します。
まず、2つの銘柄の価格系列に理想的な相関関係があった場合、つまり、同じ方向に同じ割合で変化した場合、系列間の差はゼロになり、利益を得ることができません。なぜなら、どの株も高すぎたり安すぎたりすることはないからです。
第二に、相関関係は、長期的には2つの株の関係に関する十分な情報を提供しません。 たとえば、大規模で多様な株式ポートフォリオを取り上げます。 これらの株式も株価指数に含め、ポートフォリオ内の株式のウェイトはインデックス内のウェイトによって決定されるようにします。 ポートフォリオは長期的にはインデックスに従って動くはずですが、インデックスにはあるがポートフォリオにはない株式が異常な価格変動を起こす期間があります。 その結果、ポートフォリオとインデックスの経験的相関はしばらくの間非常に低くなる可能性があります。 このため、分析では、単純にそのようなポートフォリオを破棄し、お金を稼ぐ機会を逃します。 したがって、相関はペアを識別するための良い方法ではありません。
ペアを識別するには共和分を使用することをお勧めします。
共和分
多くの場合、経済シリーズの安定性を確保するために、違いを利用します。 これにより、次の統合の定義が得られます。
時系列は統合注文と呼ばれます k そして指定されている xt simI(k) 彼と彼の違いが注文次第なら k−1 包括的非定常、およびその順序の違い k 静止しています。
実際の結果を得るには、値のみが必要です k=0 そして k=1 。 もし k=0 、その後、シリーズは静止し、簡潔にするためにそのようなシリーズを示します I(0) 。 のために k=1 シリーズは、固定増分 (1次の差)で非定常であり、簡潔にするために、このようなシリーズを以下に示します。 I(1) 。
2つありますか I(1) 行 xt そして yt 。 さらに、それらの線形結合 yt− betaxt は I(0)。 この場合、行 xt そして yt 共統合と呼ばれる:
varepsilont=yt− betaxt simI(0)。
本質的に、共和分は非定常系列の回帰です。 それが意味するのは varepsilont の平均がゼロである場合、このシリーズはゼロから大きく逸脱することはほとんどなく、多くの場合ゼロレベルを超えます。 言い換えると、時々、正確なバランスまたはそれに近い状態が達成されます。
価格の対数の共積分
価格間だけでなく、対数間の共和分も考慮することができます。 残念ながら、2つの株式の価格の対数間の共和分は、2つの株式の価格間の共和分よりも明白でなく、直観的ではありません。 しかし、対数の場合に共和分が可能なのはなぜですか?
これは、「効果的な市場仮説」、オプション価格設定モデル、および伊藤補題によって説明されます。 実際、効果的な市場の仮説には厳密な形式化はありません。 この仮説は、資産の価格がバランスの取れた自発的な需要と供給の結果である流動的な市場では、現在の価格が市場のプレーヤーが利用できるすべての情報を正確に反映することを示唆しています。 将来の価格の変化は、「ニュース」の結果に過ぎない可能性があります。これは定義上、予測不能であるため、将来の日付に対する最良の価格予測は、単に今日の価格です。 つまり、今日の価格は昨日の価格にランダム要素を加えたものです。
効率的な市場仮説は、基礎となるオプション価格設定モデルに関連しています。 このモデルの基本的な前提は、原資産の価格が S 幾何学的ブラウン運動(GBM)プロセスを満たします。
fracdSS= mudt+ sigmadW、
どこで mu そして \シグマ -資産の価格と収益性のボラティリティのオフセットである定数 W Wienerプロセス、つまり増分 dW 独立しており、平均と分散がゼロの正規分布 dt 。
GBM方程式が効率的な市場仮説にどのように関係しているかを見るには、伊藤の補題をそれに適用する必要があります。 何で構成されていますか? 変数の値を仮定する x 確率微分方程式(SDE)に従う
dx= mudt+ sigmadW、
どこで W ウィナープロセスであり、 mu そして \シグマ -変数に依存する関数 x そして t 。 また、関数 f 変数に依存 x そして t そして派生物を持っています frac partialf partialt 、 frac partialf partialx 、 frac partial2f partialx2 。 伊藤の補題は、この関数は方程式に従うと述べている
df=( frac partialf partialt+ mu frac partialf partialx+ frac sigma22 frac partial2f partialx2)dt+ sigma frac partialf partialxdW
実際、伊藤の補題はSDEの変数を変更するための式であり、特定の条件下では特定のSDEの関数もSDEです。
GBM方程式に戻り、次の形式に変換します
dS= muSdt+ sigmaSdW。
想定 f=f(S、t) 、伊藤の補題により、
df=( frac partialf partialt+ muS frac partialf partialS+ frac sigma2S22 frac partial2f partialS2)dt+ sigmaS frac partialf partialSdW
機能を紹介します f(S)= lnS 。 以来
frac partial lnS partialS= frac1S、 frac partial2 lnS partialS2=− frac1S2、 frac partial lnS partialt=0、
私達は得る:
$$ display $$ d \ lnS=(\ frac {\ partial \ lnS} {\ partial t} + \ mu S \ frac {\ partial \ lnS} {\ partial S} + \ frac { \ sigma ^ 2 S ^ 2} {2} \ frac {\ partial ^ 2 \ lnS} {\ partial S ^ 2})dt + \ sigma S \ frac {\ partial \ lnS} {\ partial S } dW = \\ =(0 + \ mu S \ frac {1} {S}-\ frac {\ sigma ^ 2 S ^ 2} {2} \ frac {1} {S ^ 2})dt + \ sigma S \ frac {1} {S} dW =(\ mu-\ frac {\ sigma ^ 2} {2})dt + \ sigma dW。$$ display $$
方程式
d lnS=( mu− frac sigma22)dt+ sigmadW
個別の形式で書き換え可能
Delta lnSt=c+ varepsilont、
どこで c= mu− sigma2/2 、そして varepsilont simNID(0、 sigma2) 、つまり、ここにプロセスがあります varepsilont 静止しているだけでなく、ホワイトノイズです。 定常プロセスの概念はホワイトノイズよりも広く、定常プロセスの期待値は一定ですが、ホワイトノイズの場合のようにゼロである必要はありません。
上記の式の離散バージョンは、次のように記述できます。
lnSt=c+ lnSt−1+ varepsilont。
この方程式はランダムウォークモデル(RW)です。これは通常、効率的な金融市場の価格の対数をモデル化するために使用され、例です。 I(1) プロセス。 したがって、共和分は株価の対数にも適用できます。
一部の懐疑論者(特に私)は、GBM方程式による株価の説明の妥当性、したがって価格の対数間の共和の可能性を疑うかもしれないという事実にもかかわらず、経験的データはこの懐疑論を首尾よく払拭します。 私がチェックしたのは、価格が統合されている場合、対数も統合されていることです。
共和分テスト
最初の共和分法は、Robert EngleとClive Grangerによって発明されました。 2003年、彼らは時系列分析のための共和分法を開発したことでノーベル経済学賞を受賞しました。 彼らは賞の15年前の1987年の記事「共積分と誤り訂正:表現、推定、テスト」でそれを説明しました。
概念的には、利用可能な観察に従って、時系列が xt そして yt 共統合、帰無仮説をテストする必要があります H0: varepsilont simI(1) 行間の相互統合の欠如 xt そして yt 対立仮説に対する H1: varepsilont simI(0) 。 帰無仮説が棄却されると、共和分が認識されます。
元の共和分テストは、創業者を称えて、アングルグレンジャーテストと呼ばれていました。 これは、検証が先行する2段階のプロセスです。 xt そして yt 一次の可積分性、 xt simI(1) そして yt simI(1) 。 これについては、 定常増分に関する記事で詳しく説明しました。 実際には、Angle-Grangerテストに直接進む前に行う必要があるすべての準備作業について説明しています。 私たちがやったとしましょう。
ランク xt そして yt それらの広がりが共和分である yt− betaxt simI(0) 、つまり静止している。 Angle-Grangerテストの最初のステップは、一貫したグレードを取得することです hat beta 。 これは、線形回帰の最小二乗最小二乗法を方程式に適用することにより行われます yt= betaxt+ varepsilont 。 2番目のステップは、残留定常性をチェックすることです。 varepsilont 共和方程式のOLS推定によって得られます。
通常、ディッキーフラーテストによって定常性をチェックします。 しかし、1990年に、フィリップスとウリアリスは、記事「共和分法の残差ベースのテストの漸近特性」で、 varepsilont Dickey-Fullerテストを使用しないでください。
実際のところ、MNCは残基を「選択」して、可能な限り最小の変動を持たせるようにしているため、変数が統合されていなくても、MNCは残基を「定常」のように見せます。 このため、Dickey-Fuller検定を使用すると、非定常性仮説が頻繁に拒否されるため、共積分の仮説が誤って受け入れられます。
著者の記事を調べると、付録では重要な値を持つテーブルが提供されていることがわかりますが、かなり不正確であることがわかりました。 その後、1991年に、エングルとグレンジャーは「長期経済関係」という本を出版しました。 その中で、第13章「共和分検定の臨界値」では、マッキノンは洗練された漸近臨界値を引用しました。 t -シミュレーションによって取得され、このケースに適した統計。
1993年、McKinnonはDavidsonと共同で、「計量経済学の推定と推論」という本を出版しました。 だから varepsilont simI(0) (残差は定常的)、その後 yt− betaxt simI(0) (スプレッドも静止しています)、つまり、 xt そして yt 。
一般に、角度グレンジャー法は次のようになります:
- 評価 \ベータ OLSを使用します。
- スプレッド計算 varepsilont=yt− betaxt およびテスト varepsilont 洗練された臨界値を使用した定常性。
matlabなどの標準パッケージでは、このテストはすでに作成されていますので、使用してみましょう。
MATLABでの統合テスト
そのため、2行の株価があります。 xt そして yt 。 欲しい xt そして yt 共統合される、すなわち広がる varepsilont=yt− betaxt 静止していた。 平均がゼロの定常級数を取得したい場合は、方程式に定数を含めることができるため、スプレッドは次のようになります。 varepsilont=yt− betaxt− alpha 。
モスクワ証券取引所で得られた結果から始めましょう。これについては、 定常増分に関する記事で説明しました。 そこに5つ見つけました I(1) 行。 それらから可能なすべての組み合わせを構成し、Angle-Grangerテストを使用して共和分をチェックします。
まず、モスクワ証券取引所から解析された株価の値を保存するMicrosoft SQL Serverデータベースから必要な書類を選択し、それらを配列としてインポートします。
conn = database.ODBCConnection('uXXXXXX.mssql.masterhost.ru', 'uXXXXXX', 'XXXXXXXXXX'); curs = exec(conn, 'SELECT ALL PriceId, StockId, Date, Price FROM StockPrices WHERE StockId IN (52, 55, 67, 75, 162) AND Date >= ''2016-01-01 00:00:00.000'' AND Date < ''2017-01-01 00:00:00.000'''); curs = fetch(curs); data = curs.Data sqlquery = 'SELECT ALL StockId, ShortName, Code FROM Stocks WHERE StockId IN (52, 55, 67, 75, 162)'; curs = exec(conn, sqlquery); curs = fetch(curs); names = curs.Data close(conn);
5銘柄中4銘柄のこの配列には、252取引日の1月のデータがあります。 ただし、いずれかの株式については、トランザクションは2月にのみ完了し始めたため、データは215取引日のみです。 すべての株式が同じ長さの価格の配列を持っていることは私たちにとって非常に重要であるため、そのような状況では2つの選択肢があります。
最初のオプションは、価格の短い配列を持つ在庫を実験から除外し、より正確な結果を得るために価格測定の最大数を使用することです。 2番目のオプションは、データの一部を寄付し、実用性を高めるためにすべての共有を含めることです。 両方の実験を実施しましたが、この場合、結果に違いはありませんでしたので、1月のデータをトリムしましょう
dates = unique(datetime(data(:,3))); % Cut dates array until price of stock with StockId=67 is not empty. dates(1:37,:) = []; prices = zeros(length(dates),length(names)); for i = 1:length(names) % Indexes with current stock's data indexes = find(cell2mat(data(:,2)) == cell2mat(names(i,1))); if length(indexes) == 252 indexes(1:37,:) = []; end for j=1:length(dates) % Fill prices according to date prices(j,i) = cell2mat(data(indexes(j),4)); end end
Angle-Grangerテストは、入力として時系列の配列(この場合はサイズ)を使用するegcitest関数を使用して実行されます n\倍2 どこで n -取引日数。 出力で、この関数は、帰無仮説が棄却された場合に1に等しい論理値を返し、そうでない場合は0を返します。
私たちが解決する必要がある次のタスクは、何をストックするかです xt そしてどれ-のために yt 。 良い方法では、両方を試してから、テスト統計を比較する必要があります。 ほとんどの場合、直接回帰と逆回帰の両方があります。 場合から始めましょう xt<yt 。
識別された5つの可能なすべてのペアを構成します I(1) 自由項を使用した回帰(デフォルト)とそれを使用しない(引数 'creg'で値 'nc'で指定)の両方について、Angle-Grangerテストを実行します。
isCoint = zeros(length(nchoosek(names(:,1),2)), 3); k=1; for i=1:length(names) for j=i+1:length(names) if mean(prices(:,i)) < mean(prices(:,j)) isCoint(k,1) = cell2mat(names(j,1)); isCoint(k,2) = cell2mat(names(i,1)); testPrices(:,1) = prices(:,j); testPrices(:,2) = prices(:,i); else isCoint(k,1) = cell2mat(names(i,1)); isCoint(k,2) = cell2mat(names(j,1)); testPrices(:,1) = prices(:,i); testPrices(:,2) = prices(:,j); end isCoint(k,3) = egcitest(testPrices); isCoint(k,4) = egcitest(testPrices, 'creg', 'nc'); k = k + 1; end end
無料のメンバーを使用した回帰の場合、プログラムは代替モデルを優先して帰無仮説を2回拒否し、ティッカー(NKHP、VTRS)、(NKHP、ZHIV)を使用して共統合された株式ペアを識別します。 自由なメンバーのない回帰の場合、プログラムは代替案を支持して帰無仮説を一度拒否し、ティッカー(VSYDP、NKHP)を含む株式の統合ペアを識別します。
逆回帰の場合( yt<xt )無料のメンバーでは、プログラムは代替モデルを支持して帰無仮説を2回拒否し、ティッカー(VTRS、NKHP)、(ZHIV、NKHP)との共統合株ペアを特定します。 自由なメンバーのない回帰の場合、プログラムは代替案を支持して帰無仮説を4回拒否し、ティッカー(GRNT、VTRS)、(GRNT、VSYDP)、(GRNT、ZHIV)、(GRNT、NKHP)で共統合された株式ペアを識別します。
値を評価しましょう \ベータ そして alpha 、egcitest関数の戻り値として取得でき、スプレッドを描画します。
% NKHP and VTRS indexY = 5; indexX = 1; testPrices(:,1) = prices(:,indexY); testPrices(:,2) = prices(:,indexX); [h,pValue,stat,cValue,reg1,reg2] = egcitest(testPrices); alpha = reg1.coeff(1); beta = reg1.coeff(2); spread = reg1.res; plot(dates,spread) legend(strcat(names(indexY,3),'-',names(indexX,3)));
NKHPおよびVTRSティッカーのある株式の場合、オッズのあるスプレッドが得られます \ベータ=$37.552 そして alpha=197,4397 :
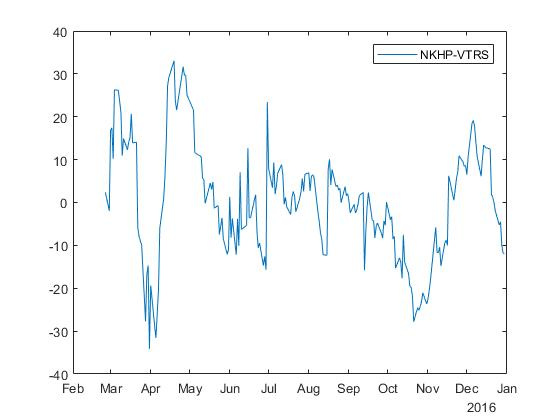
逆回帰の場合、係数で「ミラー」スプレッドを取得します \ベータ=$0.018 そして alpha=−3,0064 :
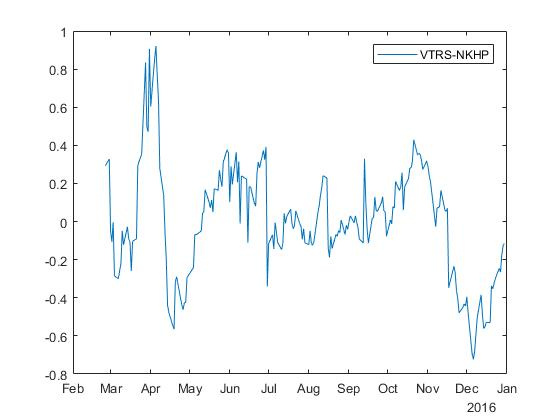
ティッカーNKHPおよびZHIVのある株式については、オッズのあるスプレッドが得られます。 \ベータ=$3.352 そして alpha=$239.347 :
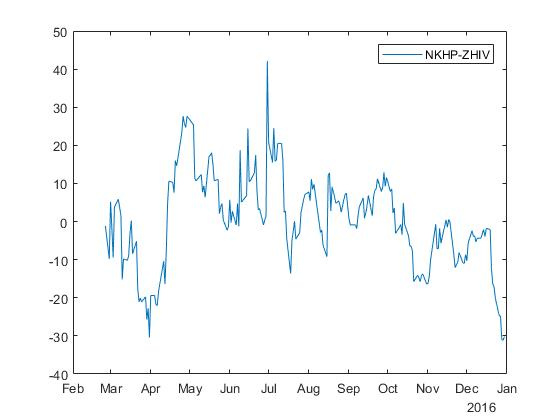
逆回帰の場合、係数付きのスプレッドを取得します \ベータ=0.2194 そして alpha=−49.6077 :
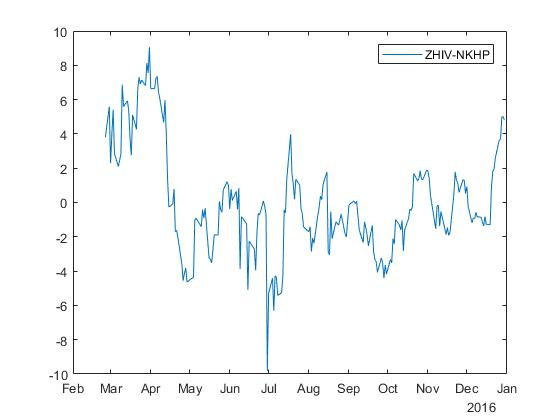
VSYDPおよびNKHPティッカーのある株式の場合、係数付きスプレッドを取得します \ベータ=$35.652 :
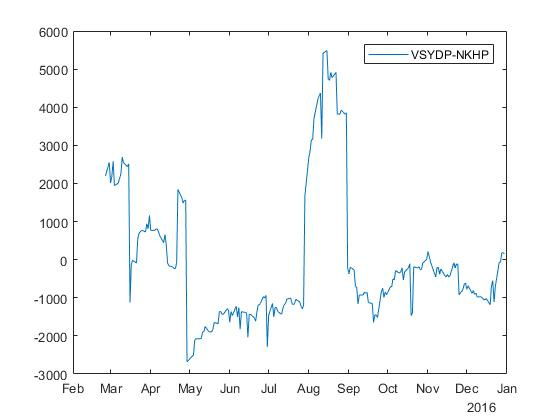
同様の実験がニューヨーク証券取引所(NYSE)で実施されました。 その結果、直接回帰の場合、無料メンバーを使用した回帰の場合は158の共統合ペアが得られ、無料メンバーを使用しない回帰の場合は130の共統合ペアが得られました。 逆回帰の場合、フリーメンバーを使用した回帰の場合は170の統合されたペアが得られ、フリーメンバーのない回帰の場合は144の統合されたペアが得られました。
回帰統計
ペア(NKHP、VTRS)の同時回帰の回帰統計を見てみましょう。
| 統計 | 直接回帰 | 逆回帰 |
|---|---|---|
| オッズ | \ベータ=$37.552 、 alpha=197,4397 | \ベータ=$0.018 、 alpha=−3,0064 |
| テスト統計 | tcalc=−3.7562 、 tcrit=−3.3654 | tcalc=−3.5906 、 tcrit=−3.3654 |
| t 統計 | t beta=21.9754 、 t alpha=53.3845 | t beta=21.9754 、 t alpha=−12.8953 |
| F 統計 | 482,9196 | 482,9196 |
| ダービン・ワトソン統計 | 0.2548 | 0.2203 |
| 決定係数 | 0.6939 | 0.6939 |
| 調整された決定係数 | 0.6925 | 0.6925 |
| 赤池情報量基準 | 1726.5 | 88.8336 |
| シュワルツ・ベイジアン情報量基準 | 1733.2 | 95.5748 |
| 漢南クイン情報基準 | 1729.2 | 91.5574 |
直接回帰と逆回帰の両方のテスト統計は、変数が \ベータ この場合、取るに足らない( tcalc<tcrit ) これは、変数が統合されている場合でも、価格がわずかに外生的であることを意味します。
スチューデント基準とフィッシャー基準を適用するには、統計が正規分布を持っている必要があります。 私たちの場合、統計はDickeyとFullerが見つけた分布と似た分布を持っています( 定常増分についての記事でも書きました)。したがって、これらの統計の計算値は非常に大きくなり、意味のあることはわかりません。
ダービン-ワトソン統計は許容できます(正の自己相関がある場合、統計はゼロになる傾向があります)。 逆回帰の場合、直接回帰の場合よりもわずかに優れています。
決定係数は受け入れ可能です(受け入れ可能なモデルの場合、決定係数は少なくとも50%であることが前提です)。 この基準から判断すると、直接回帰と逆回帰の間に違いはありません。
情報基準から判断すると、逆回帰は直接回帰に勝ちます(基準値が最小のモデルが最適であると考えられています)。
ペア(NKHP、ZHIV)の同時回帰の回帰統計を見てみましょう。
| 統計 | 直接回帰 | 逆回帰 |
|---|---|---|
| オッズ | \ベータ=$3.352 そして alpha=$239.347 | \ベータ=0.2194 そして alpha=−49.6077 |
| テスト統計 | tcalc=−3.4762 、 tcrit=−3.3654 | tcalc=−3.3878 、 tcrit=−3.3654 |
| t 統計 | t beta=24.3444 、 t alpha=137,974 | t beta=24.3444 、 t alpha=−19.8524 |
| F 統計 | 592,652 | 592,652 |
| ダービン・ワトソン統計 | 0.2614 | 0.2104 |
| 決定係数 | 0.7356 | 0.7356 |
| 調整された決定係数 | 0.7344 | 0.7344 |
| 赤池情報量基準 | 1695 | 1108.8 |
| シュワルツ・ベイジアン情報量基準 | 1701.7 | 1115.5 |
| 漢南クイン情報基準 | 1697.7 | 1111.5 |
直接回帰と逆回帰の両方のテスト統計は、変数が \ベータ この場合は重要ではありません。 Darbin-Watson統計は許容できます。逆回帰の場合は、直接回帰の場合よりもわずかに優れています。 決定係数は許容範囲です;直接回帰と逆回帰の間に違いはありません。 情報の基準によると、逆回帰は直接回帰の少し前に勝ちます。
カップル(VSYDP、NKHP)の同時回帰の回帰統計。
| 統計 | 直接回帰 |
|---|---|
| オッズ | \ベータ=$35.652 |
| テスト統計 | tcalc=−2.8339 、 tcrit=−2.7761 |
| t 統計 | 82.5035 |
| F 統計 | infty |
| ダービン・ワトソン統計 | 0.1305 |
| 決定係数 | 0.1928 |
| 調整された決定係数 | 0.1928 |
| 赤池情報量基準 | 3823.8 |
| シュワルツ・ベイジアン情報量基準 | 3827.1 |
| 漢南クイン情報基準 | 3825.1 |
可変 \ベータ 再び重要でないテスト統計によって判断します。 フィッシャーの基準は宇宙に飛び込んだ。 ダービン・ワトソン統計は受け入れられます。 決定係数は小さいため、モデルは不良であると見なされます。
結論
株式市場には十分な数の共統合された株式があります。つまり、スプレッドは定常的なプロセスです。 このようなペアの存在は、さらなる研究と安定した利益創出の基礎となりますが、次回は具体的な戦略についてお話します。
トピックについて何を読むべきですか?
ロバートF.イングル、C.W.J。グレンジャー。 統合とエラー修正:プレゼンテーション、評価、テスト//応用計量経済学。 -2015 .-- 39(3)。 -S. 107-135。
これは1987年の著者のオリジナル記事の翻訳であり、共和分法の定義はそこでより詳細に説明されています。 また、Magnusを読み続けることもできます。Magnusは、 固定増分に関する記事で推奨していますが 、共和分に関するセクションもあります 。
UPD。 2017年モスクワ取引所のペア分析