変更が必要な高速でシンプルなアルゴリズム
巡回セールスマン問題を解く方法の中で、最近傍法はその単純なアルゴリズムで引き付けられます。 元の定式化の最近傍法は、平面上の与えられた点の集合を結ぶ最小長の閉曲線を見つけることです[1]。 リソースのネットワーク上にあるMathcadパッケージのこのアルゴリズムの最も一般的な実装に注目しました[2]。 実装自体は完全に便利ではありません。たとえば、ポイント間の距離のマトリックスを導出したり、代替ルートを分析したりすることは不可能です。
この方法に対する次の非常に公正な批判がリソースに与えられています[2]。 「ルートは最適ではなく(最短ではありません)、最初の都市の選択に大きく依存します。 実際、巡回セールスマンの問題は解決されていませんが、グラフのハミルトニアンチェーンが1つ見つかりました。 そこでは、最近傍法を改善する方法が提案されました。 「次の可能な最適化ステップは、「ループの緩み」(十字線の除去)です。 別の解決策は、すべての都市(グラフの頂点)をルートの開始点としてソートし、すべてのルートの中で最も短いものを選択することです。 ただし、最後の文の実装は提供されていません。 上記のすべての状況を考えると、Pythonで上記のアルゴリズムを実装すると同時に、最小ルート長の基準に従って開始点を選択できるようにすることにしました。
ポイントの座標のランダムな値を生成するプログラムコード
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import numpy as np from numpy import exp,sqrt n=50;m=100;ib=3;way=[];a=0 X=np.random.uniform(a,m,n) Y=np.random.uniform(a,m,n) #X=[10, 10, 100,100 ,30, 20, 20, 50, 50, 85, 85, 75, 35, 25, 30, 47, 50] #Y=[5, 85, 0,90,50, 55,50,75 ,25,50,20,80,25,70,10,50,100] #n=len(X) M = np.zeros([n,n]) # for i in np.arange(0,n,1): for j in np.arange(0,n,1): if i!=j: M[i,j]=sqrt((X[i]-X[j])**2+(Y[i]-Y[j])**2)# else: M[i,j]=float('inf')# way.append(ib) for i in np.arange(1,n,1): s=[] for j in np.arange(0,n,1): s.append(M[way[i-1],j]) way.append(s.index(min(s)))# for j in np.arange(0,i,1): M[way[i],way[j]]=float('inf') M[way[i],way[j]]=float('inf') S=sum([sqrt((X[way[i]]-X[way[i+1]])**2+(Y[way[i]]-Y[way[i+1]])**2) for i in np.arange(0,n-1,1)])+ sqrt((X[way[n-1]]-X[way[0]])**2+(Y[way[n-1]]-Y[way[0]])**2) plt.title(' -%s. -%i. -%i.\n X,Y %i %i'%(round(S,3),ib,n,a,m), size=14) X1=[X[way[i]] for i in np.arange(0,n,1)] Y1=[Y[way[i]] for i in np.arange(0,n,1)] plt.plot(X1, Y1, color='r', linestyle=' ', marker='o') plt.plot(X1, Y1, color='b', linewidth=1) X2=[X[way[n-1]],X[way[0]]] Y2=[Y[way[n-1]],Y[way[0]]] plt.plot(X2, Y2, color='g', linewidth=2, linestyle='-', label=' \n ') plt.legend(loc='best') plt.grid(True) plt.show()
プログラムの結果として得られます。
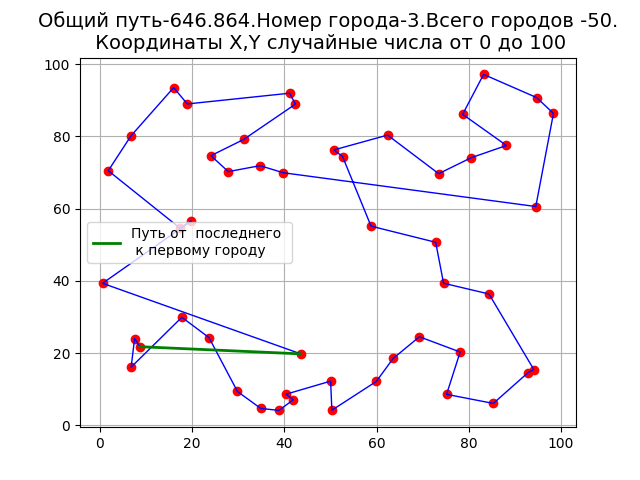
この方法の欠点は 、ループで示されるように、グラフに表示されます。 Pythonでのアルゴリズムの実装には、Mathcadよりも多くの機能があります。 たとえば、印刷するポイント間の距離のマトリックスを印刷できます。 たとえば、n = 4の場合、次のようになります。
[[ inf 43.91676312 48.07577298 22.15545245] [43.91676312 inf 54.31419355 21.7749088 ] [48.07577298 54.31419355 inf 46.92141965] [ 22.15545245 21.7749088 46.92141965 inf]]
アルゴリズムが行列の主対角線で機能するために、数値は無限に設定されます。
点のランダムな座標から、与えられたものに渡します。 リソースのデータを取得します[2]。 上記のリストで、指定された座標のモードでプログラムを実行するには、次の行からコメントを削除します。
X=[10, 10, 100,100 ,30, 20, 20, 50, 50, 85, 85, 75, 35, 25, 30, 47, 50] Y=[5, 85, 0,90,50, 55,50,75 ,25,50,20,80,25,70,10,50,100] n=len(X)
その結果、プログラムロボットを取得します。
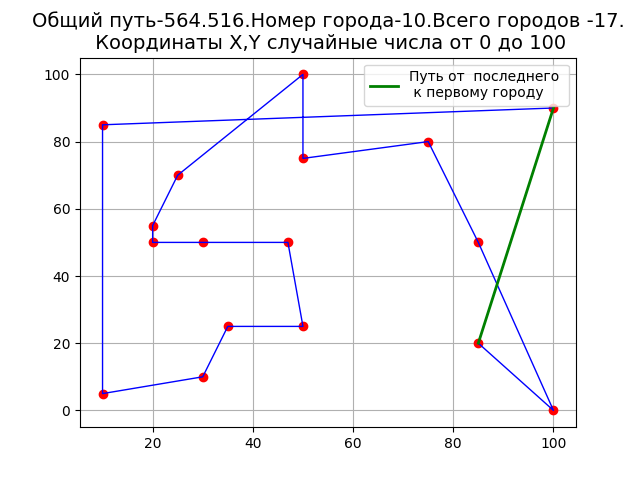
グラフから、巡回セールスマンの巡回パスが交差していることがわかります。
アルゴリズム実装の比較
私のプログラムの結果をリソース[2]のプログラムと比較するには、同じパラメーターをリソースに設定します。唯一の違いは、ポイント(都市)の番号が0から始まり、リソースで1から始まることです。その後、リソースnの都市番号= 11
ルート564、516の長さとポイントの位置は完全に一致しています。
最近傍の改善
これで、ルートの最小長の基準に従ってプログラムを変更できます。
marrutの最小長の条件から開始点を決定するためのプログラムコード(変更されたアルゴリズム)。
#!/usr/bin/env python #codi import matplotlib.pyplot as plt import numpy as np from numpy import exp,sqrt n=50;m=100;way=[];a=0 X=np.random.uniform(a,m,n) Y=np.random.uniform(a,m,n) X=[10, 10, 100,100 ,30, 20, 20, 50, 50, 85, 85, 75, 35, 25, 30, 47, 50] Y=[5, 85, 0,90,50, 55,50,75 ,25,50,20,80,25,70,10,50,100] n=len(X) RS=[];RW=[];RIB=[] s=[] for ib in np.arange(0,n,1): M = np.zeros([n,n]) for i in np.arange(0,n,1): for j in np.arange(0,n,1): if i!=j: M[i,j]=sqrt((X[i]-X[j])**2+(Y[i]-Y[j])**2) else: M[i,j]=float('inf') way=[] way.append(ib) for i in np.arange(1,n,1): s=[] for j in np.arange(0,n,1): s.append(M[way[i-1],j]) way.append(s.index(min(s))) for j in np.arange(0,i,1): M[way[i],way[j]]=float('inf') M[way[i],way[j]]=float('inf') S=sum([sqrt((X[way[i]]-X[way[i+1]])**2+(Y[way[i]]-Y[way[i+1]])**2) for i in np.arange(0,n-1,1)])+ sqrt((X[way[n-1]]-X[way[0]])**2+(Y[way[n-1]]-Y[way[0]])**2) RS.append(S) RW.append(way) RIB.append(ib) S=min(RS) way=RW[RS.index(min(RS))] ib=RIB[RS.index(min(RS))] X1=[X[way[i]] for i in np.arange(0,n,1)] Y1=[Y[way[i]] for i in np.arange(0,n,1)] plt.title(' -%s. -%i. -%i.\n X,Y '%(round(S,3),ib,n), size=14) plt.plot(X1, Y1, color='r', linestyle=' ', marker='o') plt.plot(X1, Y1, color='b', linewidth=1) X2=[X[way[n-1]],X[way[0]]] Y2=[Y[way[n-1]],Y[way[0]]] plt.plot(X2, Y2, color='g', linewidth=2, linestyle='-', label=' \n ') plt.legend(loc='best') plt.grid(True) plt.show() Z=sqrt((X[way[n-1]]-X[way[0]])**2+(Y[way[n-1]]-Y[way[0]])**2) Y3=[sqrt((X[way[i+1]]-X[way[i]])**2+(Y[way[i+1]]-Y[way[i]])**2) for i in np.arange(0,n-1,1)] X3=[i for i in np.arange(0,n-1,1)] plt.title(' ') plt.plot(X3, Y3, color='b', linestyle=' ', marker='o') plt.plot(X3, Y3, color='r', linewidth=1, linestyle='-', label=' - %s'%str(round(Z,3))) plt.legend(loc='best') plt.grid(True) plt.show ()
プログラムの結果。
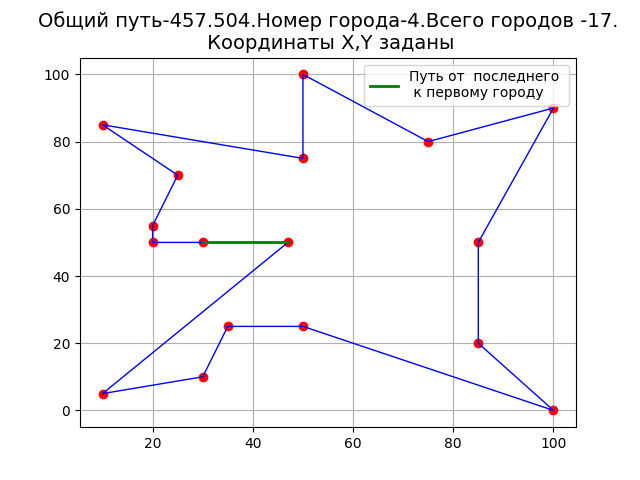
グラフにループはありません。これは、アルゴリズムの改善を示しています。

ポイント4から開始する場合のルートの長さは、他のポイントから開始する場合よりも短くなります。
- 458.662, - 0 - 463.194, - 1 - 560.726, - 2 - 567.48, - 3 - 457.504, - 4 - 465.714, - 5 - 471.672, - 6 - 460.445, - 7 - 533.461, - 8 - 532.326, - 9 - 564.516, - 10 - 565.702, - 11 - 535.539, - 12 - 463.194, - 13 - 458.662, - 14 - 457.504, - 15 - 508.045, - 16
ルートの長さのポイント数(都市)への依存
これを行うために、ランダム座標の生成に戻ります。 プログラムの結果に応じて、100のステップでポイント数を1000に増やして、1つのルート長で別のルート数のポイントまでの2行のテーブルを作成します。
プログラムを使用してデータを概算します。
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt def mnkLIN(x,y): a=round((len(x)*sum([x[i]*y[i] for i in range(0,len(x))])-sum(x)*sum(y))/(len(x)*sum([x[i]**2 for i in range(0,len(x))])-sum(x)**2),3) b=round((sum(y)-a*sum(x))/len(x) ,3) y1=[round(a*w+b ,3) for w in x] s=[round((y1[i]-y[i])**2,3) for i in range(0,len(x))] sko=round((sum(s)/(len(x)-1))**0.5,3) p=(sko*len(x)*100)/sum(y1) plt.title(' \n Y=%s*x+%s -%i -.'%(str(a),str(b),int(p)), size=14) plt.xlabel(' ', size=14) plt.ylabel(' ', size=14) plt.plot(x, y, color='r', linestyle=' ', marker='o', label=' ') plt.plot(x, y1, color='b',linewidth=1, label=' ') plt.legend(loc='best') plt.grid(True) plt.show() y=[933.516, 1282.842, 1590.256, 1767.327 ,1949.975, 2212.668, 2433.955, 2491.954, 2549.579, 2748.672] x=[100,200,300,400,500,600, 700,800, 900,1000] mnkLIN(x,y)
受け取ります。

最近傍法を使用する場合、ルートの長さとポイントの数は、指定された範囲の線形依存性によって接続されます。 [3]では、巡回セールスマン問題を解決するための主な方法の分析が行われました。 提示されたデータによると、リトルアルゴリズム、遺伝的アルゴリズム、および「近くに行く」アルゴリズムの修正が最良の結果を示しました。 この記事の巡回セールスマン問題の解決策を最近傍法で分析する追加の理由は何ですか。
結論
Pythonはフリーウェアプログラミング言語として知られています。 私が見つけたソースにあるPythonの最近傍のメソッドの実装は見つかりませんでした。 私が提案した方法の簡単な実装は、完璧からはほど遠いものですが、方法のすべてのステップを分析することができます-ポイント間の距離のマトリックスを作成し、短いルートを見つけ、アルゴリズムを変更し、ルート検索結果のグラフィック表示の機能を実現します。 これらはすべて、特に学習プロセスにおいて、明らかな理由で特別な数学的パッケージが利用できない場合に重要な要素です。 したがって、少なくともいくつかのタスクのために高価な数学的パッケージを省く無益な試みが、トレーニングの合理的な組織化だけでなく、Pythonプログラミング言語の普及にも貢献することを願っています。
記事を読んで、おそらく結果の申請を見つけてくれた皆さんに感謝します。