こんにちは、Habr！

機械学習タスクでは、モデルの品質を評価し、さまざまなアルゴリズムを比較するためにメトリックが使用されます。それらの選択と分析は、データ悪魔主義者の仕事の不可欠な部分です。

この記事では、分類問題のいくつかの品質基準を検討し、メトリックを選択する際に何が重要で、何がうまくいかないかについて説明します。

分類問題のメトリック

sklearnの有用な機能とメトリックの視覚的表示を実証するために、通信事業者の顧客の流出にデータセットを使用します。

必要なライブラリをダウンロードして、データを見てください

import pandas as pd import matplotlib.pyplot as plt from matplotlib.pylab import rc, plot import seaborn as sns from sklearn.preprocessing import LabelEncoder, OneHotEncoder from sklearn.model_selection import cross_val_score from sklearn.linear_model import LogisticRegression from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier from sklearn.metrics import precision_recall_curve, classification_report from sklearn.model_selection import train_test_split df = pd.read_csv('../../data/telecom_churn.csv')

 df.head(5)

データの前処理

 #     #   dummy-  ( ,       ) d = {'Yes' : 1, 'No' : 0} df['International plan'] = df['International plan'].map(d) df['Voice mail plan'] = df['Voice mail plan'].map(d) df['Churn'] = df['Churn'].astype('int64') le = LabelEncoder() df['State'] = le.fit_transform(df['State']) ohe = OneHotEncoder(sparse=False) encoded_state = ohe.fit_transform(df['State'].values.reshape(-1, 1)) tmp = pd.DataFrame(encoded_state, columns=['state ' + str(i) for i in range(encoded_state.shape[1])]) df = pd.concat([df, tmp], axis=1)

精度、精度、再現率

メトリック自体に進む前に、これらのメトリックを分類エラーの観点から説明するための重要な概念である混同マトリックスを導入する必要があります。

2つのクラスと、各オブジェクトがいずれかのクラスに属することを予測するアルゴリズムがあると仮定すると、分類エラーマトリックスは次のようになります。

	$y = 1$	$y = 0$
$\ hat y = 1$	真陽性（TP）	誤検知（fp）
$\ hat y = 0$	偽陰性（FN）	真のネガティブ（TN）

ここに $\ hat y$ オブジェクトに対するアルゴリズムの応答であり、 $y$ このオブジェクトの真のクラスラベルです。

したがって、分類エラーには、False Negative（FN）とFalse Positive（FP）の2種類があります。

アルゴリズムのトレーニングとエラーマトリックスの構築

 X = df.drop('Churn', axis=1) y = df['Churn'] #    train  test,        X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.33, random_state=42) #      lr = LogisticRegression(random_state=42) lr.fit(X_train, y_train) #        sklearn def plot_confusion_matrix(cm, classes, normalize=False, title='Confusion matrix', cmap=plt.cm.Blues): """ This function prints and plots the confusion matrix. Normalization can be applied by setting `normalize=True`. """ plt.imshow(cm, interpolation='nearest', cmap=cmap) plt.title(title) plt.colorbar() tick_marks = np.arange(len(classes)) plt.xticks(tick_marks, classes, rotation=45) plt.yticks(tick_marks, classes) if normalize: cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis] print("Normalized confusion matrix") else: print('Confusion matrix, without normalization') print(cm) thresh = cm.max() / 2. for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])): plt.text(j, i, cm[i, j], horizontalalignment="center", color="white" if cm[i, j] > thresh else "black") plt.tight_layout() plt.ylabel('True label') plt.xlabel('Predicted label') font = {'size' : 15} plt.rc('font', **font) cnf_matrix = confusion_matrix(y_test, lr.predict(X_test)) plt.figure(figsize=(10, 8)) plot_confusion_matrix(cnf_matrix, classes=['Non-churned', 'Churned'], title='Confusion matrix') plt.savefig("conf_matrix.png") plt.show()

精度

直感的で、明白で、ほとんど使用されていないメトリックは精度です-アルゴリズムに対する正解の割合：

\大 精 度 = f r a c T P + T N T P + T N + F P + F N

$\大精度= \ frac {TP + TN} {TP + TN + FP + FN}$

このメトリックは、不均等なクラスの問題では役に立たず、例で簡単に表示できます。

スパムメールフィルターの動作を評価したいとします。 100件の非スパムメールがあり、そのうち90件が分類子で正しく判定され（True Negative = 90、False Positive = 10）、10件のスパム文字があり、そのうち5件が分類子でも正しく判定されています（True Positive = 5、False Negative = 5）。

次に精度：

\精 度 = f r a c 5 + 90 5 + 90 + 10 + 5 = 86.4 ％

$\精度= \ frac {5 + 90} {5 + 90 + 10 + 5} = 86.4％$

ただし、すべてのメールを非スパムとして単純に予測すると、より高い精度が得られます。

\精 度 = f r a c 0 + 100 0 + 100 + 0 + 10 = 90.9 ％

$\精度= \ frac {0 + 100} {0 + 100 + 0 + 10} = 90.9％$

同時に、当初はスパムメールを特定したかったため、このモデルには予測力がまったくありません。これを克服するために、すべてのクラスの共通メトリックから個々のクラス品質指標への移行が支援されます。

精度、リコール、およびFメジャー

各クラスのアルゴリズムの品質を個別に評価するために、メトリックの精度（精度）と再現率（完全性）を導入します。

\大 精 度 = f r a c T P T P + F P

$\大精度= \ frac {TP} {TP + FP}$

\大 規 模 な リ コ ー ル = f r a c T P T P + F N

$\大規模なリコール= \ frac {TP} {TP + FN}$

精度は、分類器によってポジティブと呼ばれるオブジェクトの割合として解釈することができ、同時に、本当にポジティブであり、アルゴリズムによってポジティブクラスのすべてのオブジェクトからポジティブクラスのオブジェクトの割合が見つかったことを示しています。

正確な導入では、すべてのオブジェクトを1つのクラスに書き込むことはできません。この場合、False Positiveのレベルが増加するためです。一般に、特定のクラスを検出するアルゴリズムの能力を思い出してください。精度は、このクラスを他のクラスと区別する能力を示しています。

前述したように、分類エラーには2つのタイプがあります。FalsePositiveとFalse Negativeです。統計では、最初の種類のエラーは第1種のエラーと呼ばれ、2番目は第2種のエラーと呼ばれます。サブスクライバーの流出を決定するタスクでは、最初の種類の間違いは、忠実なサブスクライバーをアウトゴーイングサブスクライバーとして受け入れることです。これは、我々の帰無仮説はサブスクライバーが誰も去らないというものであり、この仮説を拒否するためです。したがって、第2種の間違いは、発信加入者の「合格」と帰無仮説の誤った受け入れになります。

精度とリコールは、精度とは対照的に、クラスの相関に依存しないため、不均衡なサンプルの条件に適用できます。

多くの場合、実際には、タスクはこれら2つのメトリック間の最適な（顧客の）バランスを見つけることです。典型的な例は、顧客離れを決定するタスクです。

明らかに、流出に向けて出発するすべてのクライアントを見つけることはできません。しかし、顧客維持のための戦略とリソースを決定したら、正確さとリコールの適切なしきい値を選択できます。たとえば、コールセンターのリソースが限られているため、収益性の高い顧客または退職する可能性の高い顧客のみを保持することに集中できます。

通常、アルゴリズムのハイパーパラメーターを最適化する場合（たとえば、 GridSearchCVグリッドを介して検索する場合）、1つのメトリックが使用されます。これは、テストサンプルで期待される改善です。

精度と再現率を総合的な品質基準に組み合わせるには、いくつかの異なる方法があります。 Fメジャー（一般的な場合 $\ F_ \ beta$ ）-調和平均精度と再現率：

l a r g e F_{} b e t a = （ 1 + b e t a^{2} ） c d o t f r a c p r e c i s i o n c d o t r e c a l l （ b e t a^{2} c d o t p r e c i s i o n ） + r e c a l l

$\ large \ F_ \ beta =（1 + \ beta ^ 2）\ cdot \ frac {precision \ cdot recall} {（\ beta ^ 2 \ cdot precision）+ recall}$

$\ベータ$ この場合、メトリックの精度の重みを決定し、 $\ベータ= 1$ これは調和平均です（係数は2なので、精度= 1およびリコール= 1の場合 $\ F_1 = 1$ ）

Fメジャーは、完全性と精度が1に等しい状態で最大値に達し、引数の1つがゼロに近い場合はゼロに近くなります。

Sklearnには、各クラスのリコール、精度、Fメジャー、および各クラスのインスタンス数を返す便利な_metrics.classification レポート関数があります。

 report = classification_report(y_test, lr.predict(X_test), target_names=['Non-churned', 'Churned']) print(report)

クラス	精度	思い出す	f1-スコア	サポートする
非解約	0.88	0.97	0.93	941
チャーン	0.60	0.25	0.35	159
平均/合計	0.84	0.87	0.84	1100

ここで注意すべきは、実際の慣行で普及している不均衡なクラスの問題の場合、データセットを人為的に修正してクラスの比率を均等にする手法に頼らなければならないことが多いということです。それらの多くはありますが、ここでは触れません。ここでは、いくつかの方法を見て、タスクに適した方法を選択できます。

AUC-ROCおよびAUC-PR

アルゴリズムのマテリアルレスポンス（原則として、クラスに属する確率、 SVMを個別に参照）をバイナリラベルに変換するとき、0が1になるしきい値を選択する必要があります。0.5に等しいしきい値は自然で近いように見えますが、常にそうとは限りませんたとえば、前述のクラスバランスの欠如により、最適であることがわかりました。

特定のしきい値に縛られることなく、モデル全体を評価する1つの方法は、AUC-ROC（またはROC AUC）-エラー曲線（受信者Oが C特性曲線を実行する）の下の領域（曲線下の領域）です。この曲線は、真陽性率（TPR）および偽陽性率（FPR）の座標における（0,0）から（1,1）までの線です。

\ラ ー ジ T P R = f r a c T P T P + F N

$\ラージTPR = \ frac {TP} {TP + FN}$

\大 F P R = f r a c F P F P + T N

$\大FPR = \ frac {FP} {FP + TN}$

すでにTPRを知っています。これは完全性です。FPRは、アルゴリズムが誤って予測したネガティブクラスオブジェクトの割合を示します。理想的なケースでは、分類器が間違いを犯さない場合（FPR = 0、TPR = 1）、曲線の下の面積は1に等しくなります。そうしないと、分類子が誤ってクラス確率を与えた場合、分類子が同じ数のTPとFPを生成するため、AUC-ROCは0.5になる傾向があります。

グラフ上の各ポイントは、特定のしきい値の選択に対応しています。この場合の曲線の下の領域は、アルゴリズムの品質を示しています（大きいほど良い）、これに加えて、曲線自体の急峻性が重要です-FPRを最小化することでTPRを最大化したいため、理想的には曲線が（0,1）を指す傾向があります。

ROC曲線レンダリングコード

 sns.set(font_scale=1.5) sns.set_color_codes("muted") plt.figure(figsize=(10, 8)) fpr, tpr, thresholds = roc_curve(y_test, lr.predict_proba(X_test)[:,1], pos_label=1) lw = 2 plt.plot(fpr, tpr, lw=lw, label='ROC curve ') plt.plot([0, 1], [0, 1]) plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.05]) plt.xlabel('False Positive Rate') plt.ylabel('True Positive Rate') plt.title('ROC curve') plt.savefig("ROC.png") plt.show()

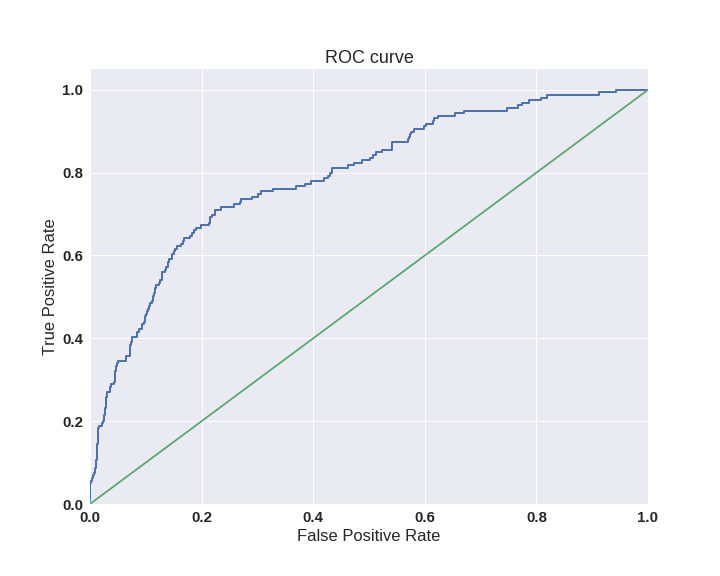
AUC-ROC基準は不均衡なクラスに耐性があり（スポイラー：悲しいことに、すべてがそれほど単純ではない）、ランダムに選択されたポジティブオブジェクトが、ランダムに選択されたネガティブオブジェクトよりも分類器によって高くランク付けされる（ポジティブになる可能性が高い）確率として解釈できます。

次のタスクを検討してください。100万件のドキュメントから100件の関連ドキュメントを選択する必要があります。 2つのアルゴリズムを機械加工しました。

アルゴリズム1は100個のドキュメントを返し、そのうちの90個が関連します。このように

T P R = f r a c T P T P + F N = f r a c 90 90 + 10 = 0.9

$TPR = \ frac {TP} {TP + FN} = \ frac {90} {90 + 10} = 0.9$

F P R = f r a c F P F P + T N = f r a c 10 10 + 999890 = $ 000

$FPR = \ frac {FP} {FP + TN} = \ frac {10} {10 + 999890} = $ 000$

アルゴリズム2は2,000のドキュメントを返しますが、そのうち90が関連しています。このように

T P R = f r a c T P T P + F N = f r a c 90 90 + 10 = 0.9

$TPR = \ frac {TP} {TP + FN} = \ frac {90} {90 + 10} = 0.9$

F P R = f r a c F P F P + T N = f r a c 1910 1910 + 997990 = $ 0.0019

$FPR = \ frac {FP} {FP + TN} = \ frac {1910} {1910 + 997990} = $ 0.0019$

最も可能性が高いのは、競合他社を背景に誤検出が非常に少ない最初のアルゴリズムを選択することです。しかし、これら2つのアルゴリズムの誤検出率の差は非常に小さく、0.0019だけです。これは、AUC-ROCがTrue Negativeと比較してFalse Positiveのシェアを測定するという事実の結果であり、2つ目の（より大きな）クラスがそれほど重要ではないタスクでは、アルゴリズムを比較するときに適切な画像を提供できない場合があります。

状況を修正するために、完全性と正確性に戻ります。

アルゴリズム1

p r e c i s i o n = f r a c T P T P + F P = 90 / （ 90 + 10 ） = 0.9

$\ precision = \ frac {TP} {TP + FP} = 90 /（90 + 10）= 0.9$

\リ コ ー ル = f r a c T P T P + F N = 90 / （ 90 + 10 ） = 0.9

$\リコール= \ frac {TP} {TP + FN} = 90 /（90 + 10）= 0.9$

アルゴリズム2

p r e c i s i o n = f r a c T P T P + F P = f r a c 90 90 + 1910 = 0.045

$\ precision = \ frac {TP} {TP + FP} = \ frac {90} {90 + 1910} = 0.045$

\リ コ ー ル = f r a c T P T P + F N = f r a c 90 90 + 10 = 0.9

$\リコール= \ frac {TP} {TP + FN} = \ frac {90} {90 + 10} = 0.9$

2つのアルゴリズムにはすでにかなりの違いがあります-精度は0.855です！

精度と再現率も曲線のプロットに使用され、AUC-ROCと同様に、その下の領域を見つけます。

ここで、小さなデータセットでは、PR曲線の下の領域は台形法で計算されるため楽観的すぎる場合がありますが、通常、このような問題には十分なデータがあります。 AUC-ROCとAUC-PRの関係の詳細については、ここをクリックしてください。

ロジスティック損失

ロジスティック損失関数は、次のように定義されます

l a r g e l o g l o s s = - f r a c 1 l c d o t s u m_{i = 1}^{l} （ y_{i} c d o t l o g （ h a t y_{i} ） + （ 1 - y_{i} ） c d o t l o g （ 1 - h a t y_{i} ） ）

$\ large logloss =-\ frac {1} {l} \ cdot \ sum_ {i = 1} ^ l（y_i \ cdot log（\ hat y_i）+（1-y_i）\ cdot log（1-\ hat y_i ））$

こっち $\ hat y$ アルゴリズムの応答は $i$ 番目の施設 $y$ -真のクラスラベル $i$ 番目のオブジェクト、および $l$ サンプルサイズ。

ロジスティック損失関数の数学的解釈についての詳細は、線形モデルに関する投稿ですでに記述されています。

このメトリックはビジネス要件にはめったに現れませんが、多くの場合kaggleタスクに現れます。

直観的に、ログロスの最小化は、不正確な予測に対する罰金によって精度を最大化するタスクとして表すことができます。ただし、分類子が答えが間違っていることを確認するために、loglossは非常に激しくペナルティを課すことに注意する必要があります。

例を考えてみましょう：

 def logloss_crutch(y_true, y_pred, eps=1e-15): return - (y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred)) print('Logloss    %f' % logloss_crutch(1, 0.5)) >> Logloss    0.693147 print('Logloss       %f' % logloss_crutch(1, 0.9)) >> Logloss       0.105361 print('Logloss       %f' % logloss_crutch(1, 0.1)) >> Logloss       2.302585

間違った答えと自信を持って分類することで、ログロスが劇的に成長したことに注意してください！

その結果、単一サイトのエラーは、サンプルエラー全体を大幅に低下させる可能性があります。このようなオブジェクトは多くの場合、外れ値であり、フィルタリングまたは個別に考慮することを忘れないでください。

loglossグラフを作成すると、すべてが適切に配置されます。

グラウンドトゥルース= 1のアルゴリズムの応答がゼロに近づくほど、エラー値が高くなり、曲線が急勾配になることがわかります。

要約すると：

マルチクラス分類の場合、メトリックを最適化するのではなく、各クラスのメトリックを注意深く監視し、問題を解決するロジックに従う必要があります
等しくないクラスの場合、トレーニングのクラスのバランスと、分類の品質を正しく反映するメトリックを選択する必要があります
メトリックの選択は、サブジェクト領域に焦点を合わせて行い、データを前処理し、場合によってはセグメント化する必要があります（裕福な顧客と貧しい顧客への分割の場合）

便利なリンク

Evgeny Sokolovのコース：モデルの選択に関するセミナー（回帰問題のメトリックに関する情報があります）
A.G.によるAUC-ROCの問題ダコノバ
他のメトリックの詳細については、 kaggleを参照してください。使用された競合へのリンクが各メトリックの説明に追加されました
不均衡なサンプルのトレーニングに関するBogdan Melnik（別名ld86）のプレゼンテーション

謝辞

この記事を手伝ってくれたmephistopheiesとmadrugadoに感謝します。

機械学習のメトリック