修正（またはノイズ耐性）コードは、データ送信中に発生したエラーを検出し、幸運であれば修正できるコードです。 それらについて何も聞いていない場合でも、ZIPアーカイブ内のファイルのリストにある略語CRC、またはメモリバー上のECCの表記に出会った可能性があります。 そして誰かが、おそらく、DVD-ROMをスクラッチしても、エラーなしでデータが読み取られるのはどうしてだろうと思ったのではないでしょうか。 もちろん、傷の厚さがセンチメートルではなく、ディスクを半分に切断しなかった場合。

ご想像のとおり、このすべてに修正コードが関係しています。 実際、ECCは「エラー修正コード」、つまり「エラー修正コード」の略です。 また、CRCはデータのエラーを検出するアルゴリズムの1つです。 彼はそれらを修正することはできませんが、これはしばしば必要ではありません。

それが何であるか見てみましょう。

記事を理解するのに特別な知識は必要ありません。 ベクトルと行列が何であるか、それらがどのように乗算されるか、そしてそれらの助けを借りて線形方程式系を書く方法を理解するのに十分です。

注意！ 多くのテキストといくつかの写真。 私はすべてを説明しようとしましたが、鉛筆と紙がなければ、テキストは少しわかりにくいかもしれません。

エラーチャンネル

最初に、修正するエラーの原因を理解します。 次の課題に直面しています。 複数のデータブロックを送信する必要があり、各データブロックは2進数のチェーンでエンコードされています。 結果として生じるゼロと1のシーケンスは、通信チャネルを介して送信されます。 しかし、実際の通信チャネルはしばしばエラーを起こしやすいことが起こりました。 一般的に、エラーにはさまざまな種類があります。余分な数字やある種の深byが表示される場合があります。 ただし、チャネルでは1つの変更のみが可能な状況、およびその逆の状況のみを考慮します。 繰り返しになりますが、簡単にするために、このような置き換えも同様に考えられます。

エラーはありそうもない出来事です（そうでなければ、なぜ一般にそのようなチャネルが必要なのですか、どこにエラーがありますか？）、これは2つのエラーの確率は少ないが、3つはすでに非常に小さいことを意味します。 境界を「これは確かに不可能です」と概説して、許容可能な確率値を選択することができます。 これにより、チャンネル内で $$$k$ 間違い。 これは、通信チャネルの機能です。

簡単にするために、次の表記法を紹介します。 送信したいデータが固定長のバイナリシーケンスであるとします。 0と1で混同しないように、大文字のラテン文字（ $$$A$ 、 $$$B$ 、 $$$C$ 、...）。 正確に何を送信するかは、一般的には重要ではありません。最初は文字で作業する方が簡単です。

エンコードとデコードは、まっすぐな矢印（ $$$\右矢印$ ）、および通信チャネルを介した伝送-波状の矢印（ $$$\ rightsquigarrow$ ） 伝送のエラーが強調されます。

たとえば、メッセージのみを送信したい場合 $$$A = 0$ そして $$$B = 1$ 。 最も単純なケースでは、ゼロと1でエンコードできます（驚き！）：

$$

$$\ begin {aligned} A＆\ to 0、\\ B＆\ to1。\ end {aligned}$$

エラーが発生したチャネルでの送信は次のように記述されます。

$$

$$A \ to 0 \ rightsquigarrow \下線{1} \ to B.$$

文字をエンコードするゼロと1のチェーンは、コードワードと呼ばれます。 この単純なケースでは、コードワードは $$$0$ そして $$$1$ 。

トリプルコード

何らかの修正コードをビルドしてみましょう。 誰かが私たちの声を聞いていないとき、私たちは通常何をしますか？ 2回繰り返します：

$$

$$\ begin {aligned} A＆\ to 00、\\ B＆\ to 11 to \ end {aligned}$$

確かに、これはあまり役に立ちません。 実際、1つのエラーが考えられるチャネルを考えてみましょう。

$$

$$A \ to 00 \ rightsquigarrow 0 \下線{1} \ to ?.$$

受け取ったときにどのような結論を導き出すことができますか $$$01$ ？ 同一の番号が2つないため、間違いがありましたが、どのカテゴリにあるのかは明らかです。 たぶん最初に、手紙が渡された $$$B$ 。 または多分2番目に、転送されました $$$A$ 。

つまり、結果のコードはエラーを検出しますが、修正はしません。 まあ、悪くもありません。 しかし、私たちはさらに先に進んで、数字を3倍にします。

$$

$$\ begin {aligned} A＆\ to 000、\\ B＆\ to 111. \ end {aligned}$$

チェックイン：

$$

$$A \ to 000 \ rightsquigarrow 0 \下線{1} 0 \ to A ??$$

受け取った $$$010$ 。 ここには2つの可能性があります。 $$$B$ そして、2つのエラーがありました（極端な数で）、またはこれ $$$A$ そして、1つの間違いがありました。 一般に、1つのエラーの確率は2つのエラーの確率よりも高いため、最も妥当な仮定は、手紙が送信されたということです。 $$$A$ 。 信じることは真実を意味するものではありませんが、そのため、その横に疑問符があります。

通信チャネルで最大1つのエラーが発生する可能性がある場合、2つのエラーの最初の仮定は不可能になり、1つのオプションのみが残ります-文字が送信されました $$$A$ 。

彼らは、そのようなコードについて、1つのエラーを修正すると言います。 彼は2つも検出しますが、すでに間違って修正します。

もちろん、これは最も単純なコードです。 エンコードは簡単で、デコードも簡単です。 より多くのトークンがあります-これはゼロが送信されたことを意味し、1つは1つを意味します。

少し考えれば、2つのエラーを修正するコードを提供できます。 これは、1つのビットを5回繰り返すコードになります。

コード間の距離

トリプルコードを詳しく見てみましょう。 そのため、単一のエラーを修正する作業コードを取得しました。 しかし、あなたはすべての良いものにお金を払わなければなりません：それは3分の1をエンコードします。 あまり効果的ではありません。

とにかく、なぜこのコードが機能するのですか？ 1つのエラーを排除するために3倍にする必要があるのはなぜですか？ 確かにすべての理由があります。

このコードの仕組みについて考えてみましょう。 直感的に、すべてが明確です。 ゼロと1は2つの異なるシーケンスです。 それらは十分に長いので、1回のミスで外観が大きく損なわれることはありません。

合格してもいいですか $$$000$ しかし、受け取った $$$001$ 。 このチェーンは元のチェーンに似ていることがわかります。 $$$000$ 上より $$$111$ 。 また、他のコードワードがないため、選択は明らかです。

しかし、「もっと似ている」とはどういう意味ですか？ そして、すべてが簡単です！ 2つのチェーンが一致する文字が多いほど、類似性が高くなります。 ほとんどすべてのキャラクターが異なる場合、チェーンは互いに「遠く」離れています。

値を入力できます $$$d（\ alpha、\ beta）$ チェーンの対応する数字の異なる数字の数に等しい $$$\ alpha$ そして $$$\ベータ$ 。 この値は、ハミング距離と呼ばれます。 この距離が大きいほど、2つのチェーンの類似性は低くなります。

例えば $$$d（010、010）= 0$ 、対応する位置の数値はすべて等しいが、 $$$d（010101、011011）= 3$ 。

ハミング距離は、下動距離と呼ばれます。 結局のところ、実際には、距離はいくらですか？ これは、2つのポイントの近接性を示すいくつかの特性であり、次の記述が当てはまります。

1. ポイント間の距離は負ではなく、ポイントが一致する場合にのみゼロに等しくなります。
2. 両方向の距離は同じです。
3. 3番目のポイントを通るパスは、直接パスより短くありません。

かなり合理的な要件。

数学的には、これは次のように書くことができます（これは、私たちにとって有益ではありませんが、興味を引くためです）。

1. $$$d（x、y）\ geqslant 0、\ quad d（x、y）= 0 \ Leftrightarrow x = y;$
2. $$$d（x、y）= d（y、x）;$
3. $$$d（x、z）+ d（z、y）\ geqslant d（x、y）$ 。

読者自身が、ハミング距離についてこれらの特性が満たされていることを確認することをお勧めします。

周辺

したがって、異なるチェーンを仮想空間のポイントと見なし、それらの間の距離を見つけることができます。 確かに、ハミング距離が平面上の距離と一致するように、紙に長いチェーンを配置しようとすると、失敗する可能性があります。 しかし、心配する必要はありません。 それにもかかわらず、これは独自の法律を持つ特別な空間です。 そして、「距離」のような言葉は私たちが推論するのを助けるだけです。

続けましょう。 距離について話すと、近所のようなものを紹介できます。 ご存じのように、ポイントの近傍は、中心を中心とする特定の半径のボールです。 ボール？ 他に何のボール！ 私たちはコードについて話している。

しかし、すべては簡単です。 結局のところ、ボールとは何ですか？ これは、指定されたポイントから半径と呼ばれる特定の距離以上離れていないすべてのポイントのセットです。 ポイントがあり、距離があり、ボールがあります。

だから、コードワードの近所を言ってみましょう $$$000$ 半径1-これは、それから1以下の距離にあるすべてのコードです。つまり、1つのカテゴリ内で異なるだけです。 つまり、これらはコードです：

$$

$$\ {000、100、010、001 \}。$$

はい、コード空間のボールはとても奇妙に見えます。

見て これらはすべて、1つのエラーでチャネルで受信する可能性のあるコードです。 $$$000$ ！ これは、近隣の定義から直接続きます。 結局、各エラーは1つのカテゴリでのみチェーンを変更します。つまり、元のメッセージから1の距離でチェーンが削除されます。

同様に、チャネルで2つのエラーが発生する可能性がある場合は、何らかのメッセージを送信します $$$x$ 、近傍に属するコードの1つを取得します $$$x$ 半径2。

その後、デコードシステム全体をこのように構築できます。 ゼロと1のチェーン（新しい用語のポイント）を取得し、それがどのコードワードに該当するかを調べます。

コードはいくつのエラーを修正できますか？

コードでより多くのエラーを修正するには、周囲をできるだけ広くする必要があります。 一方、それらは交差してはなりません。 それ以外の場合、ポイントが交差点に落ちた場合、どの近隣に属しているかは明確になりません。

コードワード間のダブルコードで $$$00$ そして $$$11$ 距離は2です（両方の数字が異なります）。 したがって、半径1のボールをそれらの周りに構築すると、それらは接触します。 つまり、接点は両方のボールに属し、どちらのボールに属しているのかが明確ではありません。

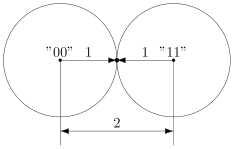
それが私たちが得たものです。 間違いがあることがわかりましたが、修正できませんでした。

興味深いことに、奇妙な空間には2つの接点があります-これらはコードです $$$01$ そして $$$10$ 。 それらから中心までの距離は1に等しいです。 もちろん、これはジオメトリでは通常不可能であるため、図面はより便利な議論のための単なる慣例です。

トリプルコードの場合、ボール間にギャップがあります。

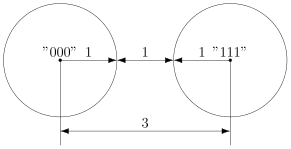
距離は常に整数であるため、ボール間の最小ギャップは1です（まあ、2つのチェーンは1.5桁で異なることはできません）。

一般的な場合、以下を取得します。

この明らかな結果は実際には非常に重要です。 最小のコード距離のコードを意味します $$$d _ {\ min}$ チャンネルで正常に動作します $$$k$ 関係の場合のエラー

$$

$$d _ {\ min} \ geqslant 2k + 1。$$

結果として得られる等価性により、特定のコードが修正するエラーの数を簡単に判断できます。 そして、いくつのエラーコードを検出できますか？ 理由は同じです。 コード検出 $$$k$ 結果が別のコードワードでない場合はエラー。 つまり、コードワードは半径の近くにあるべきではありません $$$k$ 他のコードワード。 数学的には、次のように書かれています。

$$

$$d _ {\ min} \ geqslant k + 1$$

例を考えてみましょう。 次のように4文字をエンコードします。

$$

$$\ begin {aligned} A \から10100、\\ B \から01000、\\ C \から00111、\\ D \から11011。\\ \ end {aligned}$$

異なるコードワード間の最小距離を見つけるには、ペアワイズ距離のテーブルを作成します。

	A	B	C	D
A	-	3	3	4
B	3	-	4	3
C	3	4	-	3
D	4	3	3	-

最小距離 $$$d _ {\ min} = 3$ 、つまり $$$3 \ geqslant2k + 1$ 、そのようなコードは最大で修正できることがわかります $$$k = 1$ 間違い。 彼は2つのエラーを発見しました。

例を考えてみましょう：

$$

$$A \〜10100 \ rightsquigarrow 101 \下線{1} 0。$$

受信したメッセージをデコードするには、どの文字に最も近いかを見てみましょう。

$$

$$\ begin {aligned} A：\、d（10110、10100）＆= 1、\\ B：\、d（10110、01000）＆= 4、\\ C：\、d（10110、00111）＆= 2、\\ D：\、d（10110、11011）＆=3。\ end {aligned}$$

キャラクターについて取得された最小距離 $$$A$ 、おそらく送信されたのは彼でした：

$$

$$A \ to 10100 \ rightsquigarrow 101 \ underline {1} 0 \ to A？。$$

したがって、このコードはトリプルコードと同様に1つのエラーを修正します。 ただし、トリプルコードとは異なり、4文字が既にここでエンコードされているため、より効率的です。

したがって、このようなコードを作成する際の主な問題は、コードワードをできるだけ遠くに配置することです。

デコードのために、考えられるすべての受信メッセージとそれらに対応するコードワードが示されるテーブルを使用できます。 しかし、そのようなテーブルは非常に大きくなります。 5桁の2進数を生成する小さなコードであっても機能します $$$2 ^ 5 = 32$ 受信可能なメッセージのオプション。 より複雑なコードの場合、テーブルはかなり大きくなります。

テーブルなしでメッセージを修正する方法を考えてみましょう。 解放されたメモリの便利な使用法はいつでも見つかります。

幕間：GFフィールド（2）

さらに資料を提示するには、マトリックスが必要です。 そして、あなたが知っているように、行列を掛けるとき、我々は数を足し、掛けます。 そして問題があります。 乗算ですべてが多かれ少なかれ良いなら、加算はどうですか？ 単一の2進数字のみを使用するため、1と1を追加して1つの2進数字を再度取得する方法は明確ではありません。 したがって、古典的な追加の代わりに、他の何かを使用する必要があります。

加算モジュロ2として加算演算を紹介します（XORプログラマーにはよく知られています）：

$$

$$\ begin {aligned} 0 + 0＆= 0、\\ 0 + 1＆= 1、\\ 1 + 0＆= 1、\\ 1 + 1＆=0。\ end {aligned}$$

乗算は通常どおり実行されます。 これらの操作は実際には導入されませんでしたが、数学ではフィールドと呼ばれるシステムを作成しました。 フィールドは単純なセット（この場合、0と1から）であり、その上で基本的な代数則が保存されるように加算と乗算が定義されます。 たとえば、行列と連立方程式に関する基本的な考え方は依然として真実です。 そして、逆演算として減算と除算を導入できます。

2つの要素のセット $$$\ {0、1 \}$ 導入した操作をガロア体GF（2）と呼びます。 GFはガロア体であり、2は要素の数です。

追加には、今後使用する非常に便利なプロパティがいくつかあります。

$$

$$x + x =0。$$

このプロパティは、定義から直接続きます。

$$

$$x + y = x-y。$$

これを確認するには、次を追加します $$$y$ 平等の両側に。 このプロパティは、特に、符号を変更せずに方程式の項を反対側に転送できることを意味します。

正当性を確認します

トリプルでコードに戻りましょう。

$$

$$\ begin {aligned} A＆\ to 000、\\ B＆\ to 111. \ end {aligned}$$

まず、送信中にエラーが発生したかどうかを確認するという問題を単純に解決します。 ご覧のとおり、コード自体から、受信したメッセージは、3桁すべてが等しい場合にのみコードワードになります。

行ベクトルを見てみましょう $$$x$ 3桁の。 （ほとんどすべてがあるため、ベクトルの上に矢印を描画しません。これらはベクトルまたは行列です。）

$$

$$\ドット\ rightsquigarrow x =（x_1、x_2、x_3）。$$

数学的には、3桁すべての等価性をシステムとして書くことができます。

$$

$$\左\ {\ begin {aligned} x_1＆= x_2、\\ x_2＆= x_3。 \ end {aligned} \右。$$

または、GF（2）で加算のプロパティを使用すると、次のようになります。

$$

$$\左\ {\ begin {aligned} x_1 + x_2＆= 0、\\ x_2 + x_3＆=0。\ end {aligned} \右。$$

または

$$

$$\ left \ {\ begin {aligned} 1 \ cdot x_1 + 1 \ cdot x_2 + 0 \ cdot x_3＆= 0、\\ 0 \ cdot x_1 + 1 \ cdot x_2 + 1 \ cdot x_3＆= 0. \ end {aligned} \右。$$

マトリックス形式では、このシステムは次の形式になります。

$$

$$Hx ^ T = 0、$$

どこで

$$

$$H = \ begin {pmatrix} 1＆1＆0 \\ 0＆1＆1 \ end {pmatrix}。$$

ここで転置が必要です $$$x$ 列ベクトルではなく、行ベクトルです。 それ以外の場合は、右側で行列を乗算できません。

マトリックスを呼び出します $$$H$ 検証マトリックス。 受信したメッセージが正しいコードワードである（つまり、伝送エラーがなかった）場合、このメッセージによる検証行列の積はゼロベクトルに等しくなります。

マトリックスによる乗算は、テーブルを検索するよりもはるかに効率的ですが、実際には別のテーブルがあります-これはエンコードテーブルです。 それを取り除こうとしましょう。

コーディング

だから、私たちはチェックするためのシステムを持っています

$$

$$\左\ {\ begin {aligned} x_1 + x_2＆= 0、\\ x_2 + x_3＆=0。\ end {aligned} \右。$$

彼女の決定はコードワードです。 実際には、コードワードに基づいてシステムを構築しました。 それでは、逆問題を解いてみましょう。 システム別（または、同じ、マトリックス別） $$$H$ ）コードワードを見つけます。

確かに、私たちのシステムでは、答えがすでにわかっているため、興味深いことに、別のマトリックスを使用します。

$$

$$H = \ begin {pmatrix} 1＆0＆1＆0＆0 \\ 0＆1＆1＆0＆1 \\ 0＆0＆0＆1＆1 \ end {pmatrix}。$$

対応するシステムの形式は次のとおりです。

$$

$$\左\ {\ begin {aligned} x_1 + x_3＆= 0、\\ x_2 + x_3 + x_5＆= 0、\\ x_4 + x_5＆=0。\ end {aligned} \右。$$

対応するコードのコードワードを見つけるには、それを解決する必要があります。

線形性のため、システムの2つのソリューションの合計もシステムのソリューションになります。 これは簡単に証明できます。 もし $$$a$ そして $$$b$ -システムのソリューション、それらの合計が真であるため

$$

$$H（a + b）^ T = Ha ^ T + Hb ^ T = 0 + 0 = 0、$$

それは彼女も決断だということです。

したがって、線形に独立したすべての解が見つかった場合、それらの助けを借りて、システムの一般的なすべての解を取得することができます。 これを行うには、すべての種類の金額を見つける必要があります。

まず、すべての従属用語を表現しましょう。 方程式はいくつでもあります。 独立者だけが右側にいるように表現する必要があります。 表現しやすい $$$x_1、x_2、x_4$ 。

システムがそれほど幸運でなかった場合は、3つの変数が1回発生するようにシステムを取得するために方程式を加算する必要があります。 まあ、またはガウス法を使用してください。 GF（2）でも機能します。

したがって、次のようになります。

$$

$$\ left \ {\ begin {aligned} x_1＆= x_3、\\ x_2＆= x_3 + x_5、\\ x_4＆= x_5。 \ end {aligned} \右。$$

すべての線形独立な解を得るために、各従属変数を順番に統一します。

$$

$$\ begin {aligned} x_3 = 1、x_5 = 0：\ quad x_1 = 1、x_2 = 1、x_4 = 0 \ Rightarrow x ^ {（1）} =（1、1、1、0、0）、\ \ x_3 = 0、x_5 = 1：\ quad x_1 = 0、x_2 = 1、x_4 = 1 \ Rightarrow x ^ {（2）} =（0、1、0、1、1）。 \ end {aligned}$$

これらの独立したソリューションのすべての可能な合計（つまり、コードベクトルになります）は、次のようにして取得できます。

$$

$$a_1 x ^ {（1）} + a_2 x ^ {（2）}、$$

どこで $$$a_1、a_2$ 0または1のいずれかです。 このような係数が2つあるため、すべてが可能です $$$2 ^ 2 = 4$ 組み合わせ。

しかし、見て！ ここで得た式は、行列とベクトルの乗算です。

$$

$$（a_1、a_2）\ cdot \ begin {pmatrix} 1＆1＆1＆0＆0 \\ 0＆1＆0＆1＆1 \ end {pmatrix} = aG。$$

ここの線は、線形に独立したソリューションです。 マトリックス $$$G$ 生成と呼ばれます。 これで、コーディングテーブルを自分でコンパイルする代わりに、単純にマトリックスを掛けることでコードワードを取得できます。

$$

$$a \ to aG。$$

このコードのコードワードを見つけます。 （ソースメッセージの長さは2に等しくなければならないことを忘れないでください-これは見つかったソリューションの数です。）

$$

$$\ begin {aligned} 00＆\ to 00000、\\ 01＆\ to 01011、\\ 10＆\ to 11100、\\ 11＆\ to 10111. \ end {aligned}$$

そのため、エラーを検出する既製のコードがあります。 ビジネスで確認しましょう。 01を送信し、転送中にエラーが発生したとします。 彼女のコードはそれを検出しますか？

$$

$$a=01 \to aG=01011 \rightsquigarrow x=01\underline{1}11 \to Hx^T = (110)^T \neq 0.$$

, . . , !

, , :

$$

$$G=\begin{pmatrix}1&1&1\end{pmatrix}.$$

, ( ), . , .

, . !

, . , . $$$x$ , $$$v$ 。

$$

$$e = x - v.$$

GF(2), , :

$$

$$\begin{aligned} v &= x + e,\\ x &= v + e. \end{aligned}$$

, , , , .

, $$$x$ , $$$Hx^T\neq 0$ 。 , ! , , ?

:

$$

$$s(x)=Hx^T.$$

$$

$$s(x) = Hx^T = H(v+e)^T = He^T = s(e).$$

, , .

, , . , . . ?

! , , , ? , , . .

, 5- . — .

$$$s(x)$	$$$x$
$$$000$	$$$\underline{00000}, 11100, 01011, 10111$
$$$001$	$$$\underline{00010}, 11110, 01001, 10101$
$$$010$	$$$\underline{01000}, 10100, 00011, 11111$
$$$011$	$$$01010, 10110, \underline{00001}, 11101$
$$$100$	$$$\underline{10000}, 01100, 11011, 00111$
$$$101$	$$$\underline{10010}, 01110, 11001, \underline{00101}$
$$$110$	$$$11000, \underline{00100}, 10011, 01111$
$$$111$	$$$11010, \underline{00110}, \underline{10001}, 01101$

, .

, . . , , .

, . , … .

$$

$$a = 01 \ to aG = 01011 \ rightsquigarrow x = 01 \ underline {1} 11 \ to s（x）= Hx ^ T =（110）^ T \ to e =（00100）。$$

エラーベクトルは $$$（00100）$ 、これは3番目のカテゴリのエラーを意味します。 思ったとおり。

やれやれ、すべてうまくいく！

次は？

練習するには、さまざまなテスト行列に対して推論を繰り返してみてください。 たとえば、トリプルコードの場合。

上記の論理的な続きは、巡回コードについての話です-顕著な特性を持つ線形コードの非常に興味深いサブクラスです。 しかし、その後、私は記事が非常に大きくなると思います。

詳細に興味がある場合は、ArshinovとSadovskyのすばらしい本「Codes and Mathematics」を読むことができます。 この記事で紹介されているものよりもはるかに多くのことを概説しています。 数学のコーディングに興味がある場合は、Bleichutのエラー制御コードの理論と実践を探してください。 一般的に、このトピックに関する多くの資料があります。

再び自由時間ができるようになったら、続編を書いて、巡回コードについて説明し、エンコードとデコードのプログラムの例を示します。 もちろん、由緒ある大衆に興味がない限り。