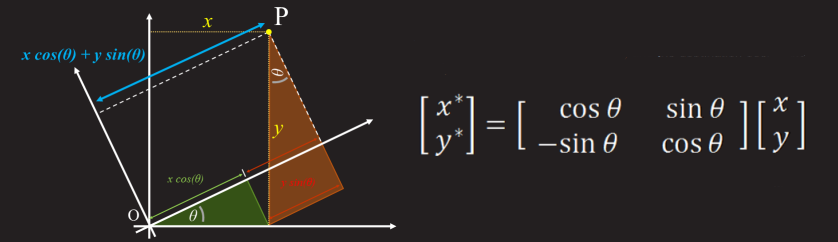
半年前、ネットでこのビデオに出会いました 。
最初の考えは、それは非常にクールであり、私はそれを二度とできないということでした。 時間が経ち、記事が読まれ、方法が研究され、私はこれの実装例を探していましたが、残念なことに、ネットワーク上に具体的なものは何もありませんでした。 CORDICアルゴリズムを使用した三角関数の計算に一度つまずいたので、FPGAで独自のイメージローテーターを作成することにしました。
CORDIC
したがって、 CORDICはCO座標Rotation D Igital C omputerの頭字語です。
これは、双曲線関数および三角関数を計算するための強力なツールです。 ほとんどのCORDICアルゴリズムは、逐次近似の方法で機能し、高レベルのプログラミング言語とHDLの両方で実装することはそれほど難しくありません。 このメソッドの数学に焦点を当てることはしません。読者は、ネットワークまたは以下のリンクでこのメソッドに精通することができます。
パブリックドメインでは、VerilogでCORDICアルゴリズムのこの実装に出会いました。 このカーネルはRotateとVectorの 2つのモードで動作します。 私たちの目的には、回転モードが適しています。 ラジアンまたは度で指定された角度から関数sinおよびcosの値を計算できます。 ライブラリは、コンベアと組み合わせバージョンの両方で構成できます。 コンベヤーは私たちの目的に適しており、 Fmaxが最大です。 16メジャーの遅延でサインとコサインの値を出力します。
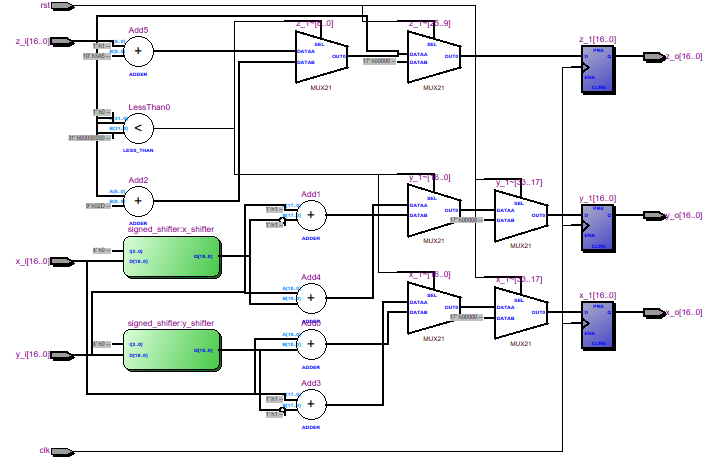
RTL Viewerでは、同じタイプの16ブロックで構成されるCORDICモジュールが表示されます。

それぞれが前の入力を受け取り、出力は次の入力に接続されます。 次のようになります。
ライブラリのコアは、最初の象限でのみ機能します。つまり、残りの3つを計算するには、π/ 2を差し引いて符号を変更する必要があります。
私が選んだアプローチはあまり正しくありません 回転した画像の品質が低下します。 これは、 Shearで行われているように、追加のデータバッファリングと複数のパスでの座標の逐次計算を使用せずに、オンザフライで座標を計算するためです。
回転子の最初のインスタンスは、象限と回転角を計算する単位です。 回転角度は、新しいフレームごとに1度ずつ増加します。 90度の角度に達すると、象限は次の角度に変わり、角度はゼロにリセットされるか、新しいフレームごとに1度ずつ減少します。
次のようになります。
always @(posedge clk) begin if (!nRst) begin cordic_angle <= 17'd0; cordic_quadrant <= 2'd0; rotator_state <= 2'd0; end else begin if (frame_changed) begin case (rotator_state) 2'd0: begin if (cordic_angle[15:8] == 8'd89) begin cordic_quadrant <= cordic_quadrant + 1'b1; rotator_state <= 2'd1; end else cordic_angle[15:8] <= cordic_angle[15:8] + 1'b1; end 2'd1: begin if (cordic_angle[15:8] == 8'd1) begin cordic_quadrant <= cordic_quadrant + 1'b1; rotator_state <= 2'd0; end else cordic_angle[15:8] <= cordic_angle[15:8] - 1'b1; end default: rotator_state <= 2'd0; endcase end end end
次に、角度値がCORDICモジュールに供給され、sinとcosの値が計算されます。
cordic CORDIC( .clk(clk), .rst(~nRst), .x_i(17'd19896), .y_i(16'd0), .theta_i(cordic_angle), .x_o(COS), .y_o(SIN), .theta_o(), .valid_in(), .valid_out() );
さらに、次の各ピクセルの座標が次の式で計算されると推測することは難しくありません。
x '= cos(角度)* x-sin(角度)* y;
y '= sin(角度)* x + cos(角度)* y;
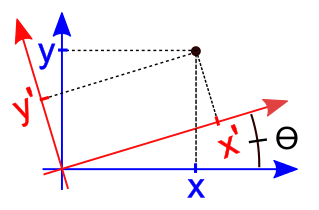
このフォームにすべてを残すと、回転は原点を中心に行われます。 この回転は私たちには適していません。画像を中心に画像の中心を回転させる必要があります。 これを行うには、画像の中心に対して計算を行う必要があります。
parameter PRECISION = 15; parameter OUTPUT = 12; parameter INPUT = 12; parameter OUT_SIZE = PRECISION + OUTPUT; parameter BUS_MSB = OUT_SIZE + 2; wire [15:0] res_x = RES_X - 1'b1; wire [15:0] res_y = RES_Y - 1'b1; assign dx = {1'b0, RES_X[11:1]}; assign dy = {1'b0, RES_Y[11:1]}; always @(posedge clk) begin delta_x <= dx << PRECISION; delta_y <= dy << PRECISION; nd
次に、値cos(角度)* x、sin(角度)* x、cos(角度)* y、sin(角度)* yを計算します。
次のように計算できます。
always @(posedge clk) begin mult_xcos <= (xi - dx) * COS; mult_xsin <= (xi - dx) * SIN; mult_ycos <= (yi - dy) * COS; mult_ysin <= (yi - dy) * SIN; end
しかし、lpm_mult メガファンクションを使用することにしました。 それらを使用すると、 Fmaxが大幅に増加します。
reg signed [BUS_MSB: 0] tmp_x, tmp_y, mult_xsin, mult_xcos, mult_ysin, mult_ycos; reg signed [BUS_MSB: 0] delta_x = 0, delta_y = 0; wire signed [11:0] dx, dy; reg signed [BUS_MSB: 0] mxsin, mxcos, mysin, mycos; reg signed [11:0] ddx, ddy; always @(posedge clk) begin ddx <= xi - dx; ddy <= yi - dy; end wire signed [BUS_MSB-1: 0] mult_xcos1; wire signed [BUS_MSB-1: 0] mult_xsin1; wire signed [BUS_MSB-1: 0] mult_ycos1; wire signed [BUS_MSB-1: 0] mult_ysin1; lpm_mult M1(.clock(clk), .dataa(COS), .datab(ddx), .result(mult_xcos1)); defparam M1.lpm_widtha = 17; defparam M1.lpm_widthb = 12; defparam M1.lpm_pipeline = 1; defparam M1.lpm_representation = "SIGNED"; lpm_mult M2(.clock(clk), .dataa(SIN), .datab(ddx), .result(mult_xsin1)); defparam M2.lpm_widtha = 17; defparam M2.lpm_widthb = 12; defparam M2.lpm_pipeline = 1; defparam M2.lpm_representation = "SIGNED"; lpm_mult M3(.clock(clk), .dataa(COS), .datab(ddy), .result(mult_ycos1)); defparam M3.lpm_widtha = 17; defparam M3.lpm_widthb = 12; defparam M3.lpm_pipeline = 1; defparam M3.lpm_representation = "SIGNED"; lpm_mult M4(.clock(clk), .dataa(SIN), .datab(ddy), .result(mult_ysin1)); defparam M4.lpm_widtha = 17; defparam M4.lpm_widthb = 12; defparam M4.lpm_pipeline = 1; defparam M4.lpm_representation = "SIGNED";
乗算後、次の各象限で符号を変更する必要がある製品を取得します。
always @(posedge clk) begin mxcos <= mult_xcos1; mxsin <= mult_xsin1; mycos <= mult_ycos1; mysin <= mult_ysin1; case (cordic_quadrant) 2'd0: begin mxsin <= -mult_xsin1; end 2'd1: begin mxcos <= -mult_xcos1; mxsin <= -mult_xsin1; mycos <= -mult_ycos1; end 2'd2: begin mxcos <= -mult_xcos1; mysin <= -mult_ysin1; mycos <= -mult_ycos1; end 2'd3: begin mysin <= -mult_ysin1; end endcase end
残っているのはこれだけです-ピクセル座標自体を計算するには:
/* I II III IV + + + - - - - - + - + + + - - + */ always @(posedge clk) begin tmp_x <= delta_x + mxcos + mysin; tmp_y <= delta_y + mycos + mxsin; end wire [15:0] xo = tmp_x[BUS_MSB] ? 12'd0: tmp_x[OUT_SIZE-1:PRECISION]; wire [15:0] yo = tmp_y[BUS_MSB] ? 12'd0: tmp_y[OUT_SIZE-1:PRECISION];
画像の境界を越えるピクセルを切り取ります。
wire [11:0] xo_t = (xo[11:0] > res_x[11:0]) ? 12'd0 : xo[11:0]; wire [11:0] yo_t = (yo[11:0] > res_y[11:0]) ? 12'd0 : yo[11:0];
そして、メモリ内の彼のアドレス:
//addr_out <= yo[11:0] * RES_X + xo[11:0];
そして再び、 lpm_multを使用します。
reg [11:0] xo_r, yo_r; always @(posedge clk) begin xo_r <= xo_t; yo_r <= yo_t; end wire [28:0] result; lpm_mult M5(.clock(clk), .dataa(RES_X[11:0]), .datab(yo_r[11:0]), .result(result)); defparam M5.lpm_widtha = 12; defparam M5.lpm_widthb = 12; defparam M5.lpm_pipeline = 1; defparam M5.lpm_representation = "UNSIGNED"; always @(posedge clk) addr_out <= result[22:0] + xo_r[11:0];
これですべてです!
メソッドの問題
上で述べたように、このアプローチには多くの欠点があります。 計算エラーのため、出力画像に穴が表示されます;回転角が大きいほど、穴が多くなります。 これは、新しい画像の寸法が元の画像の寸法よりも大きいためにも発生します。 この効果はエイリアシングによって開始され、これに対処する方法があります。たとえば、前の記事で説明したメディアンフィルターなどです。
後続の各フレームの前に、前のフレームのメモリを消去しても新しい画像がきれいな背景で取得されるように害はありませんが、時間がかかり、1つのフレームをスキップする必要があります。
この方法の唯一の利点は、実装の容易さと処理速度です。 座標はその場で計算されます。
ここから来たのは
関連リンク
→ ロシア語のCORDIC
→ ダミー用CORDIC
→ CORDIC FAQ
Quartusのプロジェクトアーカイブ
→ Yandexディスクへのリンク。