3月5日、Technocubの最終ラウンド-学童向けのオリンピックのプログラミングが行われました。 今年は3000人が参加し、そのうち400人が決勝に進みました。 ファイナルの結果とタスクの分析をご覧ください。
A. アンドリューとソックス
B. 会場は変更できません
C. アンドリューシャとカラフルなボール
D. イノセントとフットボールリーグ
E. 地下研究所
F. アクセルとビットランドのマーストン
G. アンドリューシャと生活の障壁
H. バスとイントラネット
Technocubとは何ですか？ これは、MSTUと連携してMail.Ru Groupによって編成された、8〜11年生の学生向けのプログラミングオリンピックです。 バウマンとMIPT。 入門（オンライン）、予選（オンライン）、最終（対面）の3段階で構成されています。
入門ラウンド -Codeforcesプラットフォームを探索するためのオンラインラウンド。 彼らは、システムを理解するために2つの簡単な問題を解決するように招待されています。 このようなラウンドは、各予選の前に開催されます。 その結果は、オリンピックグリッドの最終評価に影響しません。
予選ラウンド -Codeforcesプラットフォームでのオンラインラウンド。 結果によると、最高のプログラマーが決勝に進みます。 このようなラウンドでは、それぞれ6つの問題を解決することが提案されています。 最終段階に到達するには、これらのラウンドの少なくとも1つで選択を渡す必要があります。
最終ラウンドは、オリンピアードの学内ステージです。 2017年3月にモスクワ物理技術研究所とモスクワ州立工科大学でモスクワで開催されます。 バウマン。 参加者は、Codeforceプラットフォーム上のコンピューターの問題を解決するために招待されます。
受賞。 2017年、Technocubの受賞者と受賞者は、大学への入学、MIPTおよびMSTUへの入学の特別条件に応じて、第3レベルのオリンピックの恩恵を受けます。 バウマン。
すべての常勤の参加者は賞品を受け取ります。 通常、これらはチャンピオンシップのロゴTシャツです。 最初の3つの場所では、Appleテクノロジーという形で貴重な賞品も提供され、勝者はTechnocupです。 受賞者の表彰は、Mail.Ru Groupのオフィスで行われます。そこでは、開発者とチャットして仕事を見ることができます。
Technocub 2017の受賞者
2017年、テクノクブカでの勝利は、モスクワ州立大学SSCの11年生で、1年前に2位になったモスクワのアレクサンドラ・ドロズドワが優勝しました。 ヴィーツェプスクのアーサー・ペチュホフスキーがリーダーリストの2行目に、モスクワのウラジミール・ロマノフが3行目にいた。 結果の完全版はこちらでご覧いただけます 。 受賞者の皆さん、おめでとうございます！
最終ラウンドのタスクの分析
決勝の参加者は、3時間で8つの問題を解決するよう提案されました。 3人のリーダーはそのうちの7人に対処しました。 別の17人が6つのタスクを克服し、32人が5つのタスクに対処しました。
A.アンドリューとソックス
テストごとの制限時間-2秒
テストごとのメモリ制限-256メガバイト
入力-標準入力
出力-標準出力
アンドリューシャは非常にきちんとした整頓された少年なので、彼はいつも部屋で秩序を保っています。 特に、彼は自分の物をクローゼットに入れることに非常に注意を払っています。
今日、彼は困難な仕事に直面しました-靴下をクローゼットに入れること。 Andryushaには、元々バッグに折りたたまれているn種類の靴下があります。 靴下のペアには1からnまでの番号が付けられています。 アンドレイは靴下をペアでクローゼットに入れたいと思っています。 これを行うには、バッグから靴下を1つずつ取り出し、靴下を引っ張るたびに、すでにペアを引っ張っているかどうかを確認します。 そうでない場合、つまり現在のつま先のペアがまだバッグの中にあることを意味し、アンドリューシャは現在のつま先を彼の前のテーブルに置きます。 それ以外の場合、彼は現在の靴下とクローゼットのペアを削除します。
アンドリューシャはとても気配りがあり、靴下をバッグから取り出した順番を覚えていました。 今、彼は疑問に思った、そして同時にテーブルの上に彼の前に置く靴下の最大数は何でしたか？ アンドリューシャがこの質問に答えるのを手伝ってください。
入力データ
最初の行には、単一の整数n （1≤n≤10 5 ）-靴下のペアの数が含まれています。
2行目には、スペースx 1 、 x 2 、...、 x 2 n （1≤x i≤n）で区切られた2 n個の数字が含まれています。 つまり、番号x iは、アンドリューシュのi番目の順序がペアx iから靴下を得たことを意味します。
アンドリューシャが各ペアから正確に2つの靴下を取り出したことは保証されています。
インプリント
1行に1つの数字を印刷します。これは、かつてアンドリューシャの前のテーブルにあった靴下の最大数です。
例
入力データ
1
1 1
インプリント
1
入力データ
3
2 1 1 3 2 3
インプリント
2
ご注意
最初の例では、Andryushaはバッグの最初のペアから靴下を取り出し、テーブルに置きます。 その後、彼は次の靴下を取り出します。これは最初のペアのもので、両方の靴下をすぐにクローゼットに入れます。 したがって、最大1つの靴下がテーブルに置かれます。
2番目の例で何が起こるか考えてみましょう。
- まず、テーブルには何もありません。アンドリューシャはペア番号2から靴下を取り出します。
- テーブルの上には靴下があります（2）。 アンドレイは、ナンバー1のペアから靴下を取り出し、テーブルの上に置きます。
- 靴下はテーブルの上にあります（1、2）。 Andryushaはペア1から靴下を取り出しますが、そのような靴下はすでにテーブルにあります。 したがって、アンドリューシャは両方の靴下をクローゼットに入れます。
- テーブルの上には靴下があります（2）。 Andreiはペア3から靴下を取り出し、テーブルに置きます。
- 靴下はテーブルの上にあります（2、3）。 Andreiはペア番号2から靴下を取り出しますが、そのような靴下はすでにテーブルにあります。 したがって、アンドリューシャは両方の靴下をクローゼットに入れます。
- テーブルの上には靴下があります（3）。 Andreiはペア番号3から靴下を取り出しますが、そのような靴下はすでにテーブルにあります。 したがって、アンドリューシャは両方の靴下をクローゼットに入れます。
したがって、一度に最大2つの靴下がテーブルに置かれます。
実装する簡単なタスク。 各タイプの靴下がテーブルにあるかどうかを配列に保存し、靴下の数とこの数量の最大値も保存します。 次に、ソックスを1つずつ処理し、必要なすべての値を更新します。
難易度： O （ n ）時間と記憶。
B.会場は変更できません
テストごとの制限時間-5秒
テストごとのメモリ制限-256メガバイト
入力-標準入力
出力-標準出力
Bytesitiのメインストリートには、南から北への長い直線があります。 直線での方向付けの便宜上、最南の家から北に向かってメートル単位で測定された座標が入力されています。
現在、通りのいくつかのポイントにn人の友人がいて、 i番目の友人は座標x iメートルのポイントにあり、通りに沿った南または北の2つの方向のいずれかで毎秒最大速度v iメートルで移動できます。
あなたの仕事は、メインストリートのある時点でn人の友人全員が会うことができる最小時間を決定することです。 友達が出会うポイントは整数座標を持つ必要がないことに注意してください。
入力データ
最初の行には、単一の整数n （2≤n≤60 000）-友人の数が含まれます。
2行目には、 n個の整数x 1 、 x 2 、...、 x n （1≤x i≤10 9 ）-メートル単位の友人の現在の座標が含まれます。
3行目には、 n個の整数v 1 、 v 2 、...、 v n （1≤v i≤10 9 ）が含まれます。1秒あたりのメートルでの友人の最大速度です。
インプリント
n人すべてが1地点で会うことができる最小時間（秒単位）を出力します。
絶対誤差または相対誤差が10-6を超えない場合、回答は正しいとみなされます。 正式には、あなたの答えをaとし、審査員の答えをbとしましょう。 あなたの答えは正しいとみなされます 。
例
入力データ
3
7 1 3
1 2 1
インプリント
2.000000000000
入力データ
4
5 10 3 2
2 3 2 4
インプリント
1.400000000000
ご注意
最初の例では、すべての友人が2秒後にポイント5で会うことができます。 これを行うには、最初の友人が常に最高速度で南へ行き、2番目と3番目の友人が最高速度で北へ行く必要があります。
回答によるバイナリ検索を使用します。 バイナリ検索の内部では、すべての友人がt秒以内に会えるかどうかを確認する必要があります。 この間、 i番目の友人はセグメント[ x i - tv i 、 x i + tv i ]の任意のポイントにいることができます。 会議を可能にするには、いくつかのポイントがこれらすべてのセグメントに属している必要があります。つまり、交差点が空ではない必要があります。
セグメント[ l 1 、 r 1 ]、...、[ l n 、 r n ]のセットを交差させる便利な方法は、 L = max l iおよびR = min r iを計算することです。 L≤Rの場合、[ L 、 R ]は目的の交差点です。それ以外の場合、交差点は空です。
難易度： 時間とO（n）メモリ。 ここで、εは必要な相対誤差です。
C.アンドリューシャとカラフルなボール
テストごとの制限時間-2秒
テストごとのメモリ制限-256メガバイト
入力-標準入力
出力-標準出力
アンドリューシャは子供の頃から毎日公園を歩いてきました。 公園の小道と開拓地はいつも彼とあまりにも同一であるように思われ、ある日彼はそれらを装飾して多様化することに決めました。
公園は、両側の小道で相互に接続されている（n-1）n個の空き地で構成されており、各空き地から他の遊歩道に沿って歩くことができます。
アンドリューシャは、各牧草地に一つの色のついたボールを掛けることに決めました。 ボールの色は1から始まる正の整数で設定されます。公園をより多様にするために、アンドリューシャはボールの色を特別な方法で選択することにしました。 つまり、 aとbがトラックで接続され、 bとcがトラックで接続されるように、ペアごとに異なる3つのクリアリングa 、 b 、 cについて、これらのクリアリングのボールの色がペアごとに異なるようにボールを掛けたいと考えています。
Andryushaは、ボールの購入に多額のお金を費やさないために、できるだけ少ない数の異なる色を使用したいと考えています。 Andryushaはプログラミングがあまり得意ではないので、この問題の解決を手伝ってほしいと頼まれます。
入力データ
最初の行には、単一の整数n （3≤n≤2•10 5 ）-公園内の空き地の数が含まれています。
次の（ n -1）行にはそれぞれ、2つの整数xとy （1≤x、y≤n）-次のトラックで接続された2つのクリアリングの数が含まれています。
どの牧草地からでも、パスに沿って他の牧草地に行くことができます。
インプリント
最初の行に整数kを印刷します-Andryushaが使用する必要がある色の最小数。
2行目では、 n個の整数を印刷します。i番目は、 i番目の草原に掛けたいボールの色に等しくなります。 各数値は1からkの間でなければなりません。
例
入力データ
3
2 3
1 3
インプリント
3
1 3 2
入力データ
5
2 3
5 3
4 3
1 3
インプリント
5
1 3 2 5 4
入力データ
5
2 1
3 2
4 3
5 4
インプリント
3
1 2 3 1 2
ご注意
最初の例では、条件から、公園は3つの空き地で構成され、それらは直列に接続されています：1→3→2。したがって、各空き地のボールの色はペアごとに異なる必要があります。
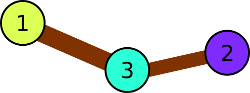
最初の例の図
2番目の例では、公園内に次の3つのクリアリングが直列に接続されています。
- 1→3→2
- 1→3→4
- 1→3→5
- 2→3→4
- 2→3→5
- 4→3→5
ここから、クリアリングの各ペアがトリプルにあることがわかります。つまり、すべてのクリアリングのボールの色はペアごとに異なっている必要があります。
2番目の例の図
3番目の例には、次のトリプルがあります。
- 1→2→3
- 2→3→4
- 3→4→5
これは、1つまたは2つの色では十分ではないことを意味し、3つの色については答えが存在し、例に示されています。
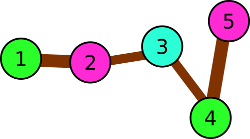
3番目の例の図
頂点vの次数がdである場合、答えは少なくともd + 1です。実際、 vの 2つの近傍はvを通る長さ3の共通パス上にあります。 さらに、 vは、3つのピークとその近隣のいずれかとの共通のパス上にあります（非近隣を使用している可能性があります）。 したがって、 vとそのすべての近傍は、ペアごとに異なる色を持つ必要があります。
この見積もりが最適であることを示します。 D + 1色でツリーの色付けを作成します。Dは頂点の最大次数です。 ツリーを任意の頂点にぶら下げ、その後、ルートとそのすべての息子を色1、2などで色付けします。 残りの頂点は、次の規則に従って色付けされます。頂点vの色がxで、親の色がyの場合、子vは1から始まり、色xとyをスキップして連続した色を受け取ります。 D + 1より大きい数値の色が必要になることは決してありません。
実装の観点から見ると、この手順は通常の詳細な手順です。
難易度： O （ n ）時間と記憶。
D.イノセントとフットボールリーグ
テストごとの制限時間-2秒
テストごとのメモリ制限-256メガバイト
入力-標準入力
出力-標準出力
イノセントは、ベイトランドで新しく設立されたフットボールリーグの社長です。 彼が直面する最初の仕事は、すべてのリーグ戦がテレビで放送されるようにすることです。 ご存知かもしれませんが、サッカーの試合中は、省略されたチーム名とライブスコアが画面に表示されます。 もちろん、ライバルクラブの略称が一致する場合は奇妙になるので、イノセントは各リーグクラブの名前を3文字に減らして、すべてのリーグチームの名前が異なるようにする方法を理解する必要があります。
各クラブの名前は2つの単語で構成されています。チームの名前と、クラブが所在する都市（「DINAMO BYTECITY」など）です。 イノセントは名前をあまりゆがめたくないので、次のような方法で各クラブの短縮名を選択したいと考えています。
1）クラブの省略名がチーム名の最初の3文字と一致したか、たとえば、上記のチームの場合は「DIN」、
2）クラブの短縮名の最初の2文字がチーム名の最初の2文字と一致し、3番目がチームの市の最初の文字と一致した。 たとえば、上記のコマンドの場合は「DIB」です。
さらに、チームxに対して名前の2番目のバリアントが選択されている場合、コマンドxの名前の最初のバリアントと一致する、短縮名の最初のバリアントが選択されているチームは存在しないはずです。 たとえば、上記のコマンドの略語が「DIB」である場合、略語の最初のバリアントが選択されているチームは略語「DIN」を持つべきではありません。 一部のチームが「DIN」という名前を取得することもできます。「DI」はチーム名の最初の2文字で、「N」は都市の最初の文字です。 もちろん、2つのチームに同じ短い名前を付けることはできません。
イノセントが各チームの略称を選択するのを助けます。 これが不可能な場合は、報告してください。 いくつかの可能な答えがある場合、イノセントはそれらのいずれかに適合します。 省略名の両方のバリエーションが特定のチームで一致する場合、イノセントはこれらのオプションのいずれか1つだけが選択されていると正式に想定します。
入力データ
最初の行には、1つの整数n （1≤n≤1000）-リーグ内のフットボールクラブの数が含まれています。
次のn行のそれぞれには、チームの名前と次のクラブの市の名前の2つの単語があります。 チーム名と都市名はどちらもラテンアルファベットの大文字で構成され、長さは少なくとも3から20以下です。
インプリント
Innocentの要件を満たす省略名を選択できない場合は、「NO」という行のみを出力します。
それ以外の場合は、最初の行に「YES」と印刷します。 次に、 n行を印刷し、各行に次のクラブの短縮名を印刷します。 入力で指定されたのと同じ順序でクラブを表示します。
可能な回答が複数ある場合は、いずれかを印刷します。
例
入力データ
2
DINAMO BYTECITY
サッカーモスクワ
インプリント
はい
DIN
フー
入力データ
2
DINAMO BYTECITY
DINAMO BITECITY
インプリント
いや
入力データ
3
プレイフットボールモスクワ
PLAYVOLLEYBALL SPB
GOGO TECHNOCUP
インプリント
はい
PLM
Pls
ゴグ
入力データ
3
ABC DEF
ABC EFG
ABD OOO
インプリント
はい
アブド
安倍
阿保
ご注意
最初の例では、両方のチームの名前の最初のバリエーションを選択できます。
2番目の例では、1つのチームが名前の最初のバリエーションを選択することは不可能であり、これらのチームの名前の最初のバリエーションが一致する場合、2番目のチームは名前の2番目のバリエーションを選択することができないため、名前を選択することはできません。
3番目の例では、最初の2つのチームの2番目の名前オプションと、3番目のチームの最初のオプションを選択できます。
4番目の例では、名前xの最初のバリアントが名前yの最初のバリアントと一致しない場合、コマンドxの選択した名前が名前yの最初のバリアントと一致することが許可されていることに注意してください。
a iとb iをそれぞれi番目のクラブの名前の最初と2番目のオプションに指定します。
すべてのa iが異なる場合、それらをすべて名前として使用できます。 それ以外の場合、一部のクラブiおよびjについてa i = a jと仮定すると、それらを同時に使用することはできません。 さらに、たとえば、このような状況でa iとb jを選択することも、条件によって禁止されています。 名前としてb iとb jを選択する必要があることがわかります。
今、他のクラブkに対して a k = b iがある場合、その名前としてb kを選択する必要があります。 このようなチェーンの依存関係は、任意のバイパスアルゴリズムで処理できます。 ある時点で同じ名前を使用する必要がある場合、解決策はありません。そうでない場合は、すべての競合を解決した後、適切な解決策が得られます。
難易度： O（n）時間とメモリがきちんと実装されている（これらの制限では、これは必要ありませんでした）。
E.地下研究所
テストごとの制限時間-1秒
テストごとのメモリ制限-256メガバイト
入力-標準入力
出力-標準出力
巨大な地下研究所で、悪の企業アンブレラは恐ろしい実験のためにクローンを作成します。 会社がアンドリューシャという名前の男の子をクローンすると、彼は彼の仲間より賢い。 アンドリューシャは、何かがおかしいことに気づきました。 彼は企業と戦うためにクローンを育て、彼らは実験室から抜け出す方法を探し始めました。 同社は地下複合施設の自己破壊のプロセスを開始する以外に選択肢がありませんでした。
実験室は、 n個の頂点とm個のエッジの連結グラフです。 このグラフのいくつかの頂点で、 k Andryushaクローンは実験室から抜け出す方法の検索を開始します。 検索プロセスでは、1秒ごとにエッジに沿って隣接する頂点に移動します。各頂点には、好きなだけクローンを作成できます。 各クローンは、ある時点で停止して検索を停止できますが、それらを確実に開始する必要があります。つまり、少なくとも1つのピークを訪れる必要があります。 さらに、出力は実験室の任意の場所に配置できるため、クローンはグラフ全体を巡回する必要があります。つまり、少なくとも1回は少なくとも1つのクローンがグラフの各頂点にアクセスする必要があります。
クローンの時間は制限されており、それぞれのクローンはそれ以上移動することができなくなります ラボが爆発する前の部屋。
タスクは、グラフの頂点にクローンを配置し、各クローンがグラフをバイパスするパスを推測することです。 さらに、各パスの頂点の数はもうないはずです 。
入力データ
最初の行には、3つの整数n 、 m 、およびk （1≤n≤2•10 5 、 n -1≤m≤2•10 5、1≤k≤n）が含まれます-グラフの頂点の数、グラフのエッジの数、クローンの数。
次のm行のそれぞれには、2つの整数x iおよびy i （1≤x i 、 y i≤n）-次のエッジで接続された2つの頂点の数が含まれます。 グラフには、ループと複数のエッジを含めることができます。
グラフが接続されていることが保証されます。
インプリント
k行を印刷します。 i番目の行の先頭に整数c i （ ） -i番目のクローンが訪問する頂点の数、そしてc i integers-彼が訪問する頂点の数、それらが訪問された順序で。 クローンが以前に訪問したことがある場合でも、クローンが訪問するたびにピークを印刷します。
答えが存在することが保証されます。
例
入力データ
3 2 1
2 1
3 1
インプリント
3 2 1 3
入力データ
5 4 2
1 2
1 3
1 4
1 5
インプリント
3 2 1 3
3 4 1 5
ご注意
最初のテストでは、クローンは1つのみで、頂点を順番に（2、1、3）巡回します。これは、6つの巡回頂点の制限に適合します。
2番目のテストでは2つのクローンがあり、それらは（2、1、3）および（4、1、5）の順序で頂点を訪問します。これは5つの訪問された頂点の制限に適合します。
グラフの任意の頂点からディープウォークを開始し、オイラーラウンド-ラウンドが頂点を訪問する順序、およびラウンドが頂点に到達するたびに、特にvから行われる各再帰呼び出しの後に頂点vが書き出される順序を書き出します。 オイラーバイパスには2 n -1個のエントリが含まれており、 k = 1の正解であることに注意してください。一般的なケースkでは、オイラーバイパスを最大⌈2 n / k⌉のサイズのk個の部分にカットし、これらの部分を応答として出力します。 条件により、各パートに少なくとも1つの頂点が必要であるため、構築された回答の空のパーツに追加する頂点はすべてあることに注意してください。
難易度： O （ n + m ）時間と記憶。
F.アクセルとビットランドのマーストン
テストごとの制限時間-5秒
テストごとのメモリ制限-256メガバイト
入力-標準入力
出力-標準出力
2人の友人、アクセルとマーストンがビットランドを旅します。 ビットランドにはn都市があり、その一部は一方向の道路で接続されています。 ビットランドの道路は歩行者と自転車です。 ビットランドでは、都市の各ペア間にいくつかの道路が存在する可能性があり、都市から都市までの道路もあります。 ただし、ビットランドの2つの道路は、同じ開始、終了、タイプを同時に持つことはできません。
友人は都市1にいて、旅行の旅程を作成したいと考えています。 アクセルは歩くのが大好きで、マーストンは自転車を好みます。 友人ごとにルートを変化させて興味深いものにするために、彼らは次のように移動した道路のタイプの交互順序を選択します。
- ルートは歩行者専用道路から始まります。
- ルートの既知の開始点を、文字（歩行者用道路）およびB（自転車用道路）の文字列sの形式で記述します。 次に、行sがルートsに追加されます
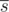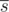どこで は、文字列sを意味します。各道路のタイプは反対に置き換えられます（すべての歩行者用道路は自転車で、逆も同様です）。
ルートを構築する最初の数ステップは、P、PV、PVVP、PVVPVPPV、PVVPVPPVVPPVPVVPなどのようになります。
その後、友人はビットランドの道路に沿って都市1で動き始め、そのたびにルートの次のシンボルに従って次の道路のタイプを選択します。 適切な道路を選択できない場合、友人は旅行を終了して帰宅します。
構築された一連の種類の道路に従っている場合、友人が旅行の最大可能期間を決定できるようにします。 友人が10 18以上の道路で構成されるパスを見つけることができる場合、長さの代わりに-1を印刷します。
入力データ
最初の行には、2つの整数nおよびm （1≤n≤500、0≤m≤2 n 2 ）-ビットランドの都市と道路の数がそれぞれ含まれています。 次のm行は道路を表します。 これらの行のi番目には、3つの整数v i 、 u iおよびt i （1≤v i 、 u i≤n、0≤t i≤1）が含まれます。ここで、 v iおよびu iは開始都市の数です。 i番目の道路の終点。tiはi番目の道路のタイプを設定します（0-歩行者用道路、1-自転車用道路）。 1≤i 、 j≤m 、 v i ≠ v j 、 u i ≠ u j 、またはt i ≠ t jのように、異なる数i 、 jの各ペアに対して保証されます。
インプリント
友人が厳密に10 18を超える長さの適切なパスを見つけることができる場合、単一の数値-1を出力します。 それ以外の場合は、適切なパスの最大長、つまり友人が通過できる道路の最大数を印刷します。
例
入力データ
2 2
1 2 0
2 2 1
インプリント
3
入力データ
2 3
1 2 0
2 2 1
2 2 0
インプリント
-1
ご注意
最初の例では、道路1で都市1から都市2に1回通過し、道路2で都市2から都市2に2回通過することで、長さ3のパスを取得できます。
2番目の例では、最初に道路1を通り、次に次のタイプの道路に応じて道路2または3を選択して、任意の長さのパスを取得できます。
A iは 、アクセスと属性のi回の繰り返しによって得られるバイナリ文字列を示します。たとえば、 A 0 = 0、 A 1 = 01などです。 また、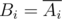 
。 定義により 
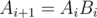、そして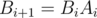 
。
行列P kとQ kを数えます。Pk / Q k （ v 、 u ）の要素は、頂点v 、 uのペアに対して1に等しいので、 vからuまで行A k / B kに対応するパスがあります。 行列P 0とQ 0は、明らかにそれぞれ0エッジと1エッジの隣接行列です。 さらに、ある頂点w P k （ v 、 w ）= Q k （ w 、 u ）= 1であり、同様の基準が機能する場合にのみ、 P k + 1 （ v 、 u ）= 1 Q k + 1 （ v 、 u ）の場合。 したがって、 P kおよびQ kを使用して、時間O （ n 3 ） に対して P k + 1およびQ k + 1を計算できます（実際、再計算はビット行列の乗算で構成されます。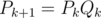 
、 
）
ここで、 P kとQ kの助けを借りて、答えを見つけます。 現在の最大の回答Lと、長さLの正しいパスに沿って頂点1から到達可能な頂点のセットSを保存します。 k 0のある値からkを降順に並べ、 Lを2 k増やすことができるかどうかを確認します。 L番目の位置の後、次の2 k文字は、ビットレコードLのユニット数のパリティに応じて文字列A kまたはB kを形成します。 S 'をAk / Bkに対応するパスに沿ってSから到達可能な頂点のセットとします。 Sが空でない場合、 Lを2 k増やしてS = Sを割り当てます。それ以外の場合は、何もしません。 最終的に、2 k 0未満の場合、 Lは最大パス長になります。
k 0 = 60を使用します。これは、2 60を超える場合、答えの正確な値に関心がないためです。 時間内に解決策が判明しました 
遅すぎる。 行列乗算のビット最適化を使用します。これにより、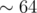 
回。
難易度： 
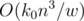時間と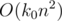 
メモリどこ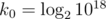 
、w = 64はビット単位のマシンワードの長さです。
G.アンドリューシャと生活の障壁
テストごとの制限時間-4秒
テストごとのメモリ制限-256メガバイト
入力-標準入力
出力-標準出力
最近、アンドリューシャは素晴らしいスロットマシンを見つけました。 それは正方形に分割された垂直に配置された板でした。 合計で、ボードには左から右に1からwまでの番号が付けられたw列があり、1からhまで下から上に番号が付けられたh行がありました。
さらに、マシンのいくつかの行にパーティションが配置されていました。 合計でn個のパーティションがあり、それらのi番目は行u iにあり、列l i〜r iのすべてのセルを占有します。 同じ行に2つのパーティションはありませんでした、Andryushaは確かにそれを思い出しました。 さらに、各行には、パーティションが存在しないセルが少なくとも1つありました。
マシンのどのコラムでも、上からボールを投げることができます。 この場合、ボールは、パーティションに遭遇するか、下からマシンから脱落するまで落下し始めました。 , , . , , . , - , . .
,
, , . , , . , i , , s i ( , u i + s i ), , . , , ( h + 1).
, . , . , 10 9 + 7.
入力データ
h , w n (1 ≤ h ≤ 10 9 , 2 ≤ w ≤ 10 5 , 0 ≤ n ≤ 10 5 ) — , .
n . i - u i , l i , r i , s i (1 ≤ u i ≤ h , 1 ≤ l i ≤ r i ≤ w , 1 ≤ s i ≤ 10 9 ) — , i - . , , , . , , , , u i .
インプリント
— 10 9 + 7.
例
10 5 1
3 2 3 10
7
10 5 2
3 1 3 10
5 3 5 10
16
10 5 2
3 1 3 7
5 3 5 10
14
10 15 4
7 3 9 5
6 4 10 1
1 1 4 10
4 11 11 20
53
ご注意
最初の例では、1つの障壁があります。2番目または3番目の列にボールを投げると、2つのボールがドロップアウトします。総回答7。
2番目の例では、ボールを左から右に列に投げた場合、ドロップされるボールの数はそれぞれ2、2、4、4、4です。
3番目の例では、ボールを左から右の列に投げる場合、ドロップされるボールの数はそれぞれ1、1、4、4、4です。最初の障壁は、その上に直接落下するボールを通過させますが、2番目の障壁から落下するボールは通過させないことに注意してください。
4番目の例では、ボールを左から右に列に投げた場合、ドロップされるボールの数はそれぞれ2、2、6、6、6、6、6、6、6、1、2、1、1、1、1です。下の図では、ボールが7列目に投入された場合が考慮されています。
1: . i - , y u i ≤ y ≤ u i + s i . x , .
各頂点をカバーする多くのアクティブなセグメントでセグメントツリーを開始します。 新しいアクティブなパーティションを追加するには、それを 
ツリーの最上部。各パーティションにこのパーティションに関するエントリを追加します。 このパーティションを削除するには、これらのエントリをすべて削除します。 現在アクティブなパーティションの中で最も高いパーティションを知りたい場合は、 xをカバーするツリーの頂点を調べ、各頂点でセット内の最も高いパーティションを調べます。 また、パーティションごとに、1つのボールを取得した結果（結果のボールの数）を保存します。 この結果を見つけるには、パーティションのアクティブ化の時点で、ツリーに対して2つのリクエストを行う必要があります（ボールが左右に落ちる場合）。 複雑なソリューションを取得します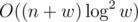 
（実行時の2番目の対数std::set
）。
解決策2：今回は、上から下に移動して、投げたすべてのボールの位置を維持しましょう。 ある時点でボールのグループが表示された場合は、それらを組み合わせてグループのサイズを記憶します。 各列では、ボールのすべてのグループをスタックに格納し、下のグループを上に格納します。
パーティション[ l 、 r ]に会いましょう。 範囲[ l 、 r ]の各列について、いくつかの下位グループがこのパーティションに分類され、それらすべてがパーティションの端に沿って（最大で2つ）グループになります。 サイズwのセグメントのツリーを作成し、各列に対して、この列の最も低いグループの高さを格納します。 ここで、少なくともセグメント[ l 、 r ]で、対応するグループをスタックから排出します（ツリーの更新を忘れずに）。 最後に、新しいグループを作成し、目的のスタックに配置します。 すべてのパーティションを処理した後に残っているボールのグループは、下から落ちます。
標準的な減価償却の推論では、合計でO （ n + w ）操作が実行されるため、ソリューションの複雑さは次のようになります。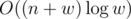 
。
H.バスとイントラネット
テストごとの制限時間-10秒
テストごとのメモリ制限-256メガバイト
入力-標準入力
出力-標準出力
町で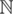 
バスルートを起動しました。これは、平面上の閉じたポリラインであり、そのすべてのリンクは座標軸に平行です。 経路上では、 m個のバスが動作し、同じ一定速度で同じ方向に破線に沿って周期的に移動します（このタスクのバス停時間は無視できます）。
バスは、等間隔で破線の最初のピークでルートに沿って動き始めます。 Tを1つのバスがルート全体を一周する時間とします。 次に、バス1は時間0、バス2-時間T / m 、3番目-時間2 T / mなどで移動を開始します。 最後に、バスmは（ m -1） T / mから始まります。 したがって、隣接するバスのすべてのペア（最後と最初を含む）間の間隔は同じです。
バスは、同じ電力のワイヤレス送信機を使用して情報を交換できます。 バスの送信機電力がDの場合、 D以下の距離にあるバス間で情報の交換が可能です。
さらに、バスにはルートの分散追跡システムが装備されています。 すべてのバスがスケジュール通りに厳密に移動するためには、システムはすべてのバス上のデータを定期的に同期する必要があります。 同期時には、バス1はバス2とバス2、バス3はバス3と情報を交換します。さらに、バスmはバス1と情報を交換します。
分析部門の従業員として、少なくとも時折同期を実行できるDの最小値を見つけるタスクを与えられました。
入力データ
最初の行には、2つの整数nとm （2≤n、m≤10 5 ）-それぞれポリラインの頂点の数とバスの数が含まれています。
次のn行は、ポリラインの頂点をその走査順に説明しています。 これらの各行には、2つの整数x i 、 y i （-1000≤x i 、 y i≤1000）-次の頂点の座標が含まれます。
ポリラインの各リンク（最後の頂点と最初の頂点の間を含む）が座標軸の1つに平行であることが保証されます。 さらに、折れ線の連続する2つの頂点は一致しません。 ポリラインには自己交差があり、1つのセグメントを数回通過することができます。
インプリント
1つの実数-問題への答えを印刷します。 絶対誤差または相対誤差が10-6を超えない場合、答えは受け入れられます。
例
入力データ
4 2
0 0
0 1
1 1
1 0
出力
1.000000000
入力データ
2 2
0 0
1 0
出力
0.000000000
ご注意
すべてのバスが1秒あたり1単位の距離を走行できるようにします。 最初の例では、0.5秒後、バスは1の距離にあるため、 D = 1を選択できます。
2番目の例では、0.5秒後に両方のバスがポイント（0.5、0）になるため、 D = 0を選択できます。
結果、7列目にボールを投げた場合
答えに対してバイナリ検索を行います。 内部では、バス1と2、2と3、...、 nと1のすべてのペアが同時にx以下の距離にあるような瞬間があるかどうかを確認する必要があります。
p （ t ）を、時刻tの後のバス1（時刻0に出発）の位置とします。 ||の場合、インスタントtを goodと呼びます。 p （ t + T / m ） -p （ t ）|| ≤x、ここで|| a - b || は、点aと点bの間の距離を意味します。 t 、 t + T / m 、...、 t +（ m -1） T / mがすべて良好であるようなモーメントtがある場合、答えは少なくともxです。
ベクトルp （ t + T / m ） -p （ t ）の2次元グラフを時間内に構築します。このため、点p （ t ）とp （ t + T / m ）がポリラインのどちら側にあるかを監視します。 各ポイントがそれぞれの側に移動する場合、ベクトルp （ t + T / m ） -p （ t ）は時間とともに線形に変化し、それによりグラフも区分的に線形になります。 ポイントの1つが左右に移動するのはO （ n ）のモーメントしかないため、2つのポインターを使用してグラフを時間O （ n ）にプロットできます。
ここで、固定xの適切なモーメントtのセットを見つけます。 差分グラフの各セグメントに対して個別にこれを行い、それから答えを一緒に構成します。 差q = p （ t + T / m ） -p （ t ）の観点から、条件||があります。 q || ≤x、ここでqは特定のセグメント上で実行されます。 これは、セグメントと円の交点を見つける標準的な問題です。これは、2次方程式を解くことや、特定のベクトルを目的の角度だけ回転させるなど、さまざまな方法で解決できます。 いずれの場合でも、結果は一定の期間または空のセットです。 グラフの一部ではqを一定に保つことができることに注意してください。この場合は個別に処理するのが最適です。
p （ t ）、 p （ t + T / m ）などの瞬間を見つける 良い場合は、セグメント[0、 T ]をm個の等しい部分にカットし、それらを互いの上に「重ね合わせ」ます。これにより、良いセグメントもパーツにカットする必要があります。 ここで、適切な瞬間tはm回カバーされるポイントです。 そのような点の検索は、走査線の標準的なアプリケーションです。
難易度：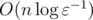 
ここで、 εは必要な相対精度です。
ニュースをフォローしてください！ 新しいイベントに関する情報を見逃さないように、Technokub Vkontakte グループに登録してください 。