🛀🏼 🈹 🍼 線形回帰について：ルーブル為替レートへのベイズのアプローチ 👩🏾‍⚕️ 🎟️ 🌬️

ルーブルの為替レートが石油のコストに直接依存していることは秘密ではありませんこの事実により、非常に興味深いモデルを構築できます。線形回帰に関する私の記事では、モデルの診断に捧げられたいくつかの質問に触れましたが、次の質問が舞台裏に残っていました。線形回帰のより効果的だが複雑すぎない代替案はありますか？従来使用されていた最小二乗法は単純で簡単ですが、他のアプローチもあります。 ~~（それほど明確ではない）~~ 。

MNCデータと診断

この記事では、ルーブル為替レートの原油価格への依存を視覚的な補助として使用して、いくつかの本質的に線形なモデルを比較します。この素晴らしい投稿を覚えていますか？ 2年後、グラフィックを更新する時が来ました。 Quandlから最新のデータをダウンロードします。コード「EIA / PET_RBRTE_D」はブレント原油のスポット価格を$で、「BOE / XUDLBK69」はロシアルーブルで1ドルのコストを隠します。

データ

library(Quandl) library(zoo) library(dplyr) oil.ts <-Quandl("EIA/PET_RBRTE_D", trim_start="2005-04-03", trim_end="2017-03-10", type="zoo", collapse="weekly") usd.ts <-Quandl("BOE/XUDLBK69", trim_start="2005-04-03", trim_end="2017-03-10", type="zoo", collapse="weekly")

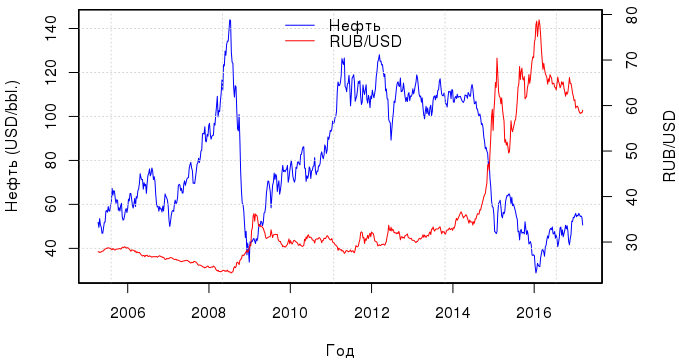
期間は2005年4月から2017年3月までです。そして、ドルでルーブルの価値を表現する場合、この期間に観察されたダイナミクスは次のとおりです。

スケジュールから判断すると、ルーブルと原油価格曲線の関係は常に追跡されていましたが、2012年以降は特に密接になりました。原則として、これらすべての年にOLSの1つの回帰を構築することはほとんど意味がありません。急激な価格変動のため、回帰の残余はマルチモーダル分布になり、すべてが不十分に記述されたモデルが得られます。したがって、2015年3月から2016年12月までの期間を考慮します。これはトレーニングのサンプルになります。 2017年のデータをテストに使用します。

関係の性質は2015年以降変化しておらず、 OLSを使用して構築された線形回帰rub _i = a + b・oil _i は統計的に有意です。

MNC

 tr.s <- "2015-03-01"; tr.e <- "2016-12-31" train <- data.frame(oil=as.vector(window(oil.ts, start=tr.s, end=tr.e)), rub=as.vector(window(rub.ts, start=tr.s, end=tr.e)), date=index(window(oil.ts, start=tr.s, end=tr.e))) %>% mutate(month=factor(format(date, "%m")), date=NULL) te.s <- "2017-01-01"; te.e <- "2017-03-15" test <- data.frame(oil=as.vector(window(oil.ts, start=te.s, end=te.e)), rub=as.vector(window(rub.ts, start=te.s, end=te.e)), date=index(window(oil.ts, start=te.s, end=te.e))) %>% mutate(month=factor(format(date, "%m")), date=NULL) fit1 <- lm(rub ~ oil, data=train) summary(fit1) ## ## Call: ## lm(formula = rub ~ oil, data = train) ## ## Residuals: ## Min 1Q Median 3Q Max ## -2.096e-03 -3.265e-04 4.510e-06 3.491e-04 1.871e-03 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 7.284e-03 3.396e-04 21.45 <2e-16 *** ## oil 1.777e-04 7.009e-06 25.35 <2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.0005883 on 94 degrees of freedom ## Multiple R-squared: 0.8724, Adjusted R-squared: 0.871 ## F-statistic: 642.7 on 1 and 94 DF, p-value: < 2.2e-16

r u b_{i} = 0.0073 + 0.000178 c d o t o i l_{i}

$rub_i = 0.0073 + 0.000178 \ cdot oil_i$

自由項を削除すると、R ²は単一にほぼ等しくなります。これには説明があります。どんなに魅力的であっても、無料の用語を無効にすることは単に不可能です（調査中のプロセスが回帰線が原点を通過することを保証しない限り）：興味のある人はここで読むことができます。 R ^2にこだわらないでください-この基準は非常に形式的です。モデルの残骸に関しては、それらは一般によく分布していますが、二峰性であるようです：

残り物

モデル診断

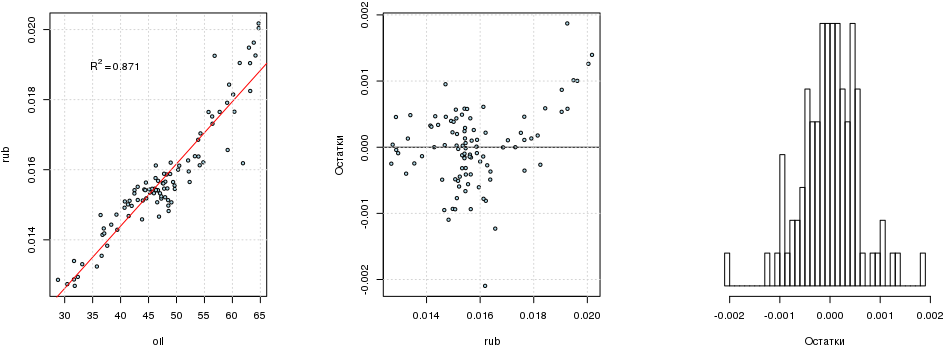
 library(lmtest) dwtest(fit1) ## ## Durbin-Watson test ## ## data: fit1 ## DW = 0.49421, p-value < 2.2e-16 ## alternative hypothesis: true autocorrelation is greater than 0 resettest(fit1) ## ## RESET test ## ## data: fit1 ## RESET = 13.999, df1 = 2, df2 = 92, p-value = 4.924e-06

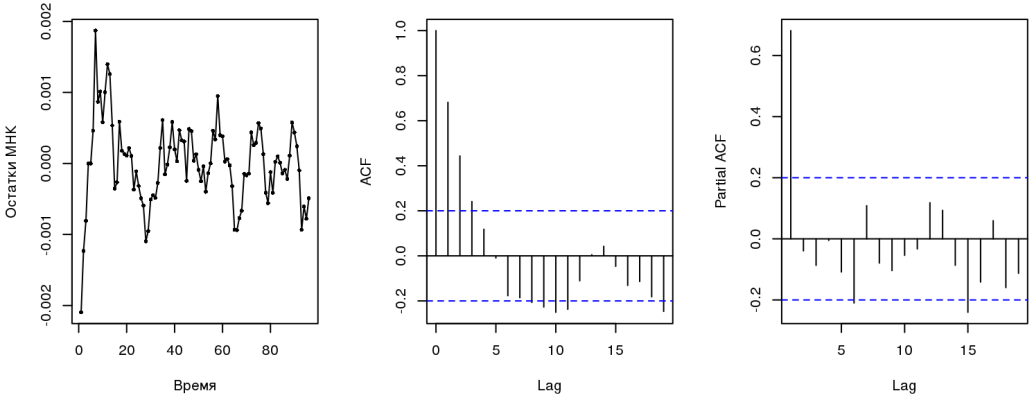
Darbin-Watson検定は、自己相関の存在（だれが考えていたでしょうか）を示します。残基の相関図は、ARタイプのプロセスを示しています（1）（これについては以下で説明します）。 RESETテストは欠落している変数を示します。これは論理的です。多くの要因がコースに影響します（またはOLSは最適なモデルではありません）。これらはすべて、 MNEの根底にある前提に違反します。計量経済学に従事している人は誰でも、そのような回帰を慎重に使用する必要があると言うでしょう。すべての推定値は偏っており、受け入れられないため、信頼区間を構築することはできません。すべてのプロパティのうち、直線性のみが保持されます。

別のトリックを思いつくことができます。おそらく依存関係は線形ではなく、多項式項を含んでいます。多かれ少なかれ最適なモデルを選択するには？相互検証またはAICなどの情報基準を使用する必要があります。線形モデルの場合、特に漸近的な挙動ではAICとCVの結果が収束するため、後者がより好きです。次のコードは、必要なことを行うだけです。1〜5の次数で多項式回帰が構築され、最小AIC基準に基づいて最適なモデルが決定されます。 poly（）関数は直交多項式を構築し、回帰で使用する必要があります。

 which.min(sapply(1:5, function(i) AIC(lm(rub ~ poly(oil, i), data=train)))) ## [1] 3

したがって、モデルは次の形式を持つこともできます。

r u b_{i} = a + b c d o t o i l_{i} + b_{2} c d o t o i l_{i}^{2} + b_{3} c d o t o i l_{i}^{3}

$rub_i = a + b \ cdot oil_i + b_2 \ cdot oil_i ^ 2 + b_3 \ cdot oil_i ^ 3$

時系列とエラー

時系列は無限に議論でき、さまざまな成功を収めています。しかし、これを知る必要があります。ルーブル為替レートと原油価格は時系列であり、これは無視できません（したがって、OLSのエラーの問題が発生します）。一部のプロセスは、単純な1次自己回帰モデルを使用して説明できます。これは、時系列の次の値が前の値と小さなエラーで十分に説明されていることを意味します。

u_{t} = c + p h i u_{t - 1} + e p s i l o n_{t} 、

$u_ {t} = c + \ phi u_ {t-1} + \ epsilon_t、$

ここで、εtはホワイトノイズです。

追加のリグレッサーを使用してARIMAモデルを作成しましょう。

有馬

 library(forecast) fit2 <- auto.arima(train$rub, xreg=train$oil) summary(fit2) ## Series: train$rub ## Regression with ARIMA(1,0,0) errors ## ## Coefficients: ## ar1 intercept train$oil ## 0.9123 0.0108 1e-04 ## se 0.0417 0.0004 0e+00 ## ## sigma^2 estimated as 1.274e-07: log likelihood=626.46 ## AIC=-1244.91 AICc=-1244.47 BIC=-1234.65 ## ## Training set error measures: ## ME RMSE MAE MPE MAPE ## Training set 1.424521e-05 0.000351317 0.0002580076 0.02303551 1.610766 ## MASE ACF1 ## Training set 0.7766594 0.02983604

このモデルに関する情報から、回帰中に摩擦_i = a + b・油_i + u _iで、誤差u _iが自己相関構造ARIMA（1、0、0）を持つことがわかります。それらは正確に1次自己回帰モデルAR（1）です。

なぜならエラー構造はおおよそわかっています。一般化最小二乗法（GLS）を試してみましょう。 GLSは、次のようなシンプルなアイデアを使用しています。システムy = Xb +εを最小二乗法で解くときに、回帰係数と共分散行列が方程式から求められた場合

b_{O L S} = （ X^{T} X ）^{- 1} X^{T} y V a r （ b_{O L S} ） = s i g m a^{2} （ X^{T} X ）^{- 1} 、

$b_ {OLS} =（X ^ TX）^ {-1} X ^ Ty \\ Var（b_ {OLS}）= \ sigma ^ 2（X ^ TX）^ {-1}、$

GLSを使用する場合、対応する方程式は次のようになります。

b_{G L S} = （ X^{T} \シ グ マ^{- 1} X ）^{- 1} X^{T} \シ グ マ^{- 1} y V a r （ b_{G L S} ） = （ X^{T} \シ グ マ^{- 1} X ）^{- 1}

$b_ {GLS} =（X ^ T \シグマ^ {-1} X）^ {-1} X ^ T \シグマ^ {-1} y \\ Var（b_ {GLS}）=（X ^ T \シグマ^ {-1} X）^ {-1}$

ここで、Σは、その構造を知ることで推定できる誤差の共分散行列です。理論的には、このようなモデルは、偏りのない、効率的な、一貫した、漸近的に通常の推定値を提供します（エイトケンの定理）。

GLS

 library(nlme) fit3 <- gls(rub ~ oil, data=train, correlation=corAR1(value=0.7, form=~1|month)) summary(fit3) ## Generalized least squares fit by REML ## Model: rub ~ oil ## Data: train ## AIC BIC logLik ## -1173.847 -1163.674 590.9237 ## ## Correlation Structure: AR(1) ## Formula: ~1 | month ## Parameter estimate(s): ## Phi ## 0.7478772 ## ## Coefficients: ## Value Std.Error t-value p-value ## (Intercept) 0.007860934 0.0004055443 19.38366 0 ## oil 0.000163683 0.0000081087 20.18601 0 ## ## Correlation: ## (Intr) ## oil -0.952 ## ## Standardized residuals: ## Min Q1 Med Q3 Max ## -2.96100735 -0.41075284 0.07903953 0.62870157 3.42607023 ## ## Residual standard error: 0.0006099571 ## Degrees of freedom: 96 total; 94 residual

r u b_{i} = 0.00786 + 0.000164 c d o t o i l_{i}

$rub_i = 0.00786 + 0.000164 \ cdot oil_i$

また、AIC基準に従ってGLSに多項式の項を含めることで利益が得られるかどうかも確認できます。

 which.min(sapply(1:5, function(i) { d <- data.frame(poly(train$oil, i), month=train$month, rub=train$rub) AIC(gls(rub ~ . - month, data=d, correlation=corAR1(value=0.7, form=~1|month))) })) ## [1] 1

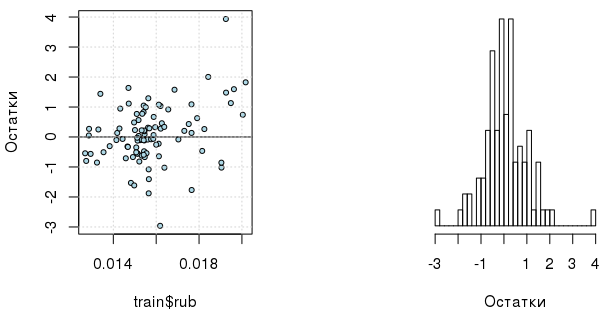
1度で十分なリグレッサーになりました。ところで、修正されたモデルエラー自体は、より興味深い分布になっています（ただし、外れ値の存在に注意するしかありません）。

ベイズ回帰と変数の確率的選択

この時点で、OLS、ARIMA（1、0、0）、AR（1）エラーのあるGLSの3つのモデルがあります。次に、問題を別の定式化で検討し、まず、たとえば多項式の項が必要かどうかを質問します。

y_{i} s i m N （ a + X_{i}^{T} c d o t b 、 t a u ） X_{i} = [x_{i} 、 x_{i}^{2} 、 x_{i}^{3} 、 x_{i}^{4} 、 x_{i}^{5}] b = [b_{1} 、 b_{2} 、 b_{3} 、 b_{4} 、 b_{5}] b_{j} = I_{j} c d o t b_{{t a u}_{j}} 、 j = 1..5 I_{j} s i m B e r n o u l l i （ p ） b_{t a u_{j}} s i m N （ 0 、 t a u_{b} ） a s i m N （ 0 、 10^{- 4} ） t a u s i m G a m m a （ 1 、 10^{- 3} ） t a u_{b} s i m G a m m a （ 1 、 10^{- 3} ） p s i m B e t a （ 2 、 9 ）

$y_i \ sim N（a + X_i ^ T \ cdot b、\ tau）\\ X_i = [x_i、x_i ^ 2、x_i ^ 3、x_i ^ 4、x_i ^ 5] \\ b = [b_1、b_2、 b_3、b_4、b_5] \\ b_j = I_j \ cdot b _ {{\ tau} _j}、\ j = 1..5 \\ I_j \ sim Bernoulli（p）\\ b _ {\ tau_j} \ sim N（0 、\ tau_b）\\ a \ sim N（0、10 ^ {-4}）\\ \ tau \ sim Gamma（1、10 ^ {-3}）\\ \ tau_b \ sim Gamma（1、10 ^ { -3}）\\ p \ sim Beta（2、9）$

ここでは、変数y _iが正規分布し、次数x _iに線形に依存することが記述されています。同様に、回帰係数は正規分布だけでなく、方程式に「存在しない」場合もあります。これは、パラメーターpのベルヌーイ分布に従うインジケーター変数I _jによって保証されます。値0または1のみを取ることができます。パラメータpは、ベータ分布から順番に取得され、パラメータτおよびτbはガンマから取得されます。したがって、事前分布を設定します。それらの正確な形はどのように知られていますか？ここで、理論はあまりわかりやすくなく、説明されたプロセスまたは直観の性質に関する実用的な概念に依存するか、情報量の少ないアプリオリ分布を指定することができます。幸いなことに、利用可能なデータが多いほど、出力はアプリオリ分布に依存しなくなります。これは、特定のデータが観測されたときにアプリオリ分布が変化するルールであるベイズ式を見ると明らかになります。

p （ t h e t a | y ） = f r a c p （ y | t h e t a ） p （ y ） p （ t h e t a ） p r o p t o p （ y | t h e t a ） p （ t h e t a ）

$p（\ theta | y）= \ frac {p（y | \ theta）} {p（y）} p（\ theta）\ propto p（y | \ theta）p（\ theta）$

ここで、p（θ| y）は事後分布、p（y |θ）は尤度、p（θ）はアプリオリ分布です。次に書くことができます：

p （ t h e t a | y_{1} ） p r o p t o p （ y_{1} | t h e t a ） p （ t h e t a ）

$p（\ theta | y_1）\ propto p（y_1 | \ theta）p（\ theta）$

さらに慣性について：

p （ t h e t a | y_{1} 、 l d o t s 、 y_{i} ） p r o p t o p （ y_{i} | t h e t a ） p （ t h e t a | y_{1} 、 l d o t s 、 y_{i - 1} ）

$p（\ theta | y_1、\ ldots、y_i）\ propto p（y_i | \ theta）p（\ theta | y_1、\ ldots、y_ {i-1}）$

しかし、分布が多かれ少なかれ有意義であることが依然として望ましい。そのため、ヒストグラムy _i （ルーブル交換レートがあります）を見ると、正規分布（または対数正規分布...）に似た曲線を見ることができます。回帰係数に関しては、ここではガウス分布の選択は、それらが正規分布しているという従来の期待によって正当化されます。

もちろん、魅力的な派生に手動で関与したい人はいないので、先験的な分布の観点からモデルを記述することができるライブラリが必要です。 Rでは、これらはrjagsであり、 R2jagsのラッパー関数でもあります。上記はすべて次のように記述されます。

ベイジアン変数選択

 library(R2jags) model1 <- "model { for (i in 1:n) { y[i] ~ dnorm(a + inprod(X[i,], b[]), tau) } for (j in 1:p) { ind[j] ~ dbern(pind) bT[j] ~ dnorm(0, taub) b[j] <- ind[j] * bT[j] } a ~ dnorm(0, 1e-04) tau ~ dgamma(1, 1e-03) taub ~ dgamma(1, 1e-03) pind ~ dbeta(2, 9) }" p <- 5 m.jags1 <- jags(data=list(y=train$rub, X=poly(train$oil, p), n=nrow(train), p=p), parameters.to.save=c("a", "b", "ind"), model.file=textConnection(model1), n.chains=1, n.iter=5000) m.jags1 ## Inference for Bugs model at "5", fit using jags, ## 1 chains, each with 5000 iterations (first 2500 discarded), n.thin = 2 ## n.sims = 1250 iterations saved ## mu.vect sd.vect 2.5% 25% 50% 75% 97.5% ## a 0.016 0.000 0.015 0.015 0.016 0.016 0.017 ## b[1] 0.011 0.007 0.000 0.006 0.013 0.017 0.023 ## b[2] 0.000 0.001 0.000 0.000 0.000 0.000 0.003 ## b[3] 0.000 0.001 0.000 0.000 0.000 0.000 0.000 ## b[4] 0.000 0.001 0.000 0.000 0.000 0.000 0.000 ## b[5] 0.000 0.001 0.000 0.000 0.000 0.000 0.000 ## ind[1] 0.764 0.425 0.000 1.000 1.000 1.000 1.000 ## ind[2] 0.046 0.210 0.000 0.000 0.000 0.000 1.000 ## ind[3] 0.034 0.180 0.000 0.000 0.000 0.000 1.000 ## ind[4] 0.031 0.174 0.000 0.000 0.000 0.000 1.000 ## ind[5] 0.045 0.207 0.000 0.000 0.000 0.000 1.000 ## deviance -848.261 15.731 -876.531 -858.633 -848.740 -838.639 -815.570 ## ## DIC info (using the rule, pD = var(deviance)/2) ## pD = 123.7 and DIC = -724.5 ## DIC is an estimate of expected predictive error (lower deviance is better).

結論は、回帰係数b ₂ 、...、b _5を持つインジケーター変数I _jの平均値はI ₁よりも₁桁小さいことを示しています。つまり、このような確率モデルでは、ルーブル交換レートが石油の価格に線形に依存すると仮定する権利が与えられます。次に、エラーの一次自己回帰の存在を考慮に入れた単純な線形モデルを作成します。

ベイズar1

 model2 <- "model { a ~ dt(0, 5, 1) b ~ dt(0, 5, 1) phi ~ dunif(-1, 0.999) tau0 ~ dgamma(1, 1e-03) tau[1] <- tau0 y[1] ~ dnorm(a + b * x[1], tau[1]) for (i in 2:n){ tau[i] <- tau0 + phi * tau[i-1] y[i] ~ dnorm(a + b * x[i], tau[i]) } }" set.seed(123) n <- nrow(test) m.jags2 <- jags(data=list(y=c(train$rub, rep(NA, n)), x=c(train$oil, test$oil), n=nrow(train)+n), parameters.to.save=c("a", "b", "phi", "y"), model.file=textConnection(model2), n.chains=1, n.iter=5000)

これは、モデルパラメーターの事後分布の様子です。

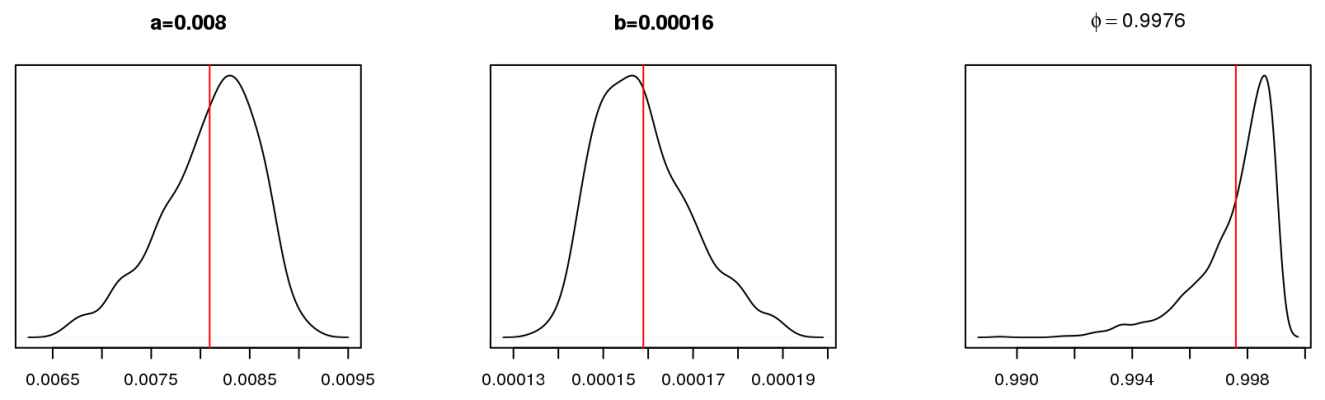
GLSモデルのパラメーターとそれほど違わないことに気付くかもしれません。パラメータの平均値の回帰式自体は、次のように記述できます。

r u b_{i} s i m N （ 0.0081 + 0.000157 c d o t o i l_{i} 、 t a u_{i} ）

$rub_i \ sim N（0.0081 + 0.000157 \ cdot oil_i、\ tau_i）$

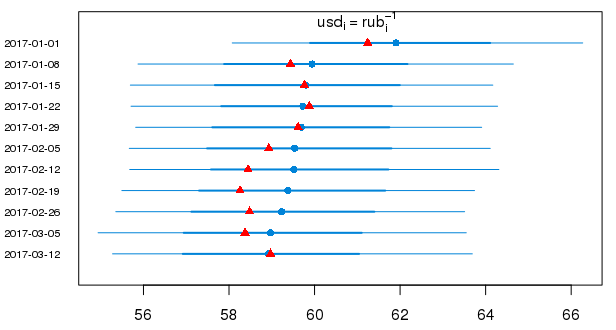
しかし、2017年のドルの予測値に対する通常の形式の95％の確率間隔（赤い三角形は真の値を示します）：

おわりに

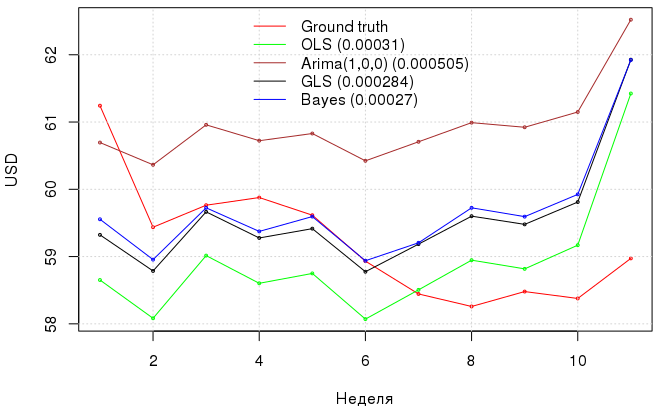
以下はモデルとそのエラーによるドル為替レートの予測を持つグラフです。これらの簡単な操作により、モデル誤差の自己回帰プロセスを考慮してベイジアンアプローチを使用した場合、OLEの3.1e-04から2.7e-04へのMAEの減少を達成し、GLSはベイジアンアプローチとほぼ同じ結果を示しましたが、道徳的支出は少なくなりました。

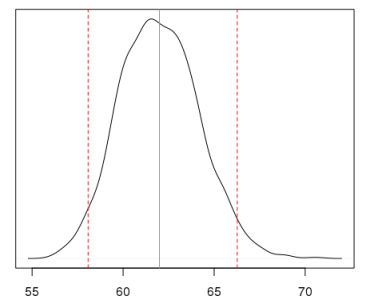
最終的に、OLSをあまり上回らないモデルが得られた場合、なぜこのような結論を出す必要があったのですか？まず、正式にMNCの前提条件に違反しません。第二に、彼らはモデルがまだ多項式項を含んでいないという確率的確認を受けました。第三に、関心のある量の確率的（信頼ではない！）間隔を取得することが可能になりました。たとえば、50.63USD / bbl。の原油価格で95％の確率でルーブルでドルがどれくらいかかるか興味がある場合、この分布を取得できます。

もちろん、確率的推論を使用したこのような回帰には、ある程度の努力と経験が必要です。一方、何かをすばやく計算する必要がある場合、分布を処理することに消極的であり、確率間隔は無関心であり、モデルエラーは相関しているため、不適切なめったに使用されない一般化最小二乗法（GLS）に注意する必要があります。 OLSのブラインド使用。さらに、auto.arima（）を忘れないでください。これにより、モデルの残りの部分の相関プロセスをすばやく評価できます。

ボーナス

ルーブル為替レートと国際準備金との間には、依然として興味深い非常に明白な相関関係があります。

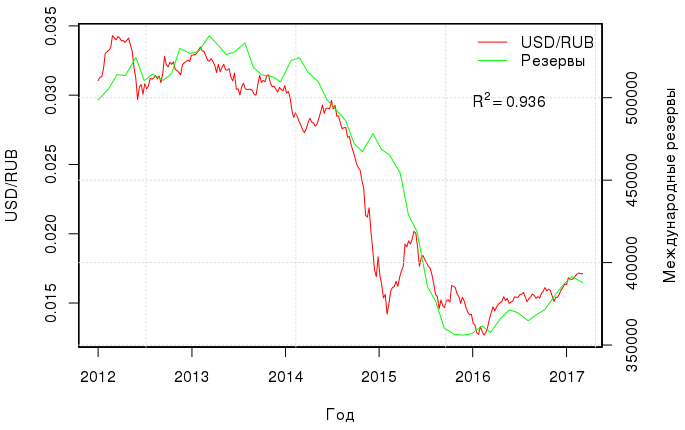
これら2つの値の間に線形回帰を作成すると、決定係数は0.936に等しくなります。 2つのリグレッサー（オイルとリザーブ）を持つモデルはR ² _adj = 0.98であり、何よりもラムゼイRESETテストは、この回帰に欠損変数がないことを確認します。ルーブルの為替レートは、石油と国際準備金のコストによって非常に説明されます。

r u b_{i} = - 8.713 c d o t 10^{- 3} + 1.458 c d o t 10^{- 4} c d o t o i l_{i} + 4.648 c d o t 10^{- 8} c d o t r e s_{i} 、

$rub_i = -8.713 \ cdot 10 ^ {-3} +1.458 \ cdot 10 ^ {-4} \ cdot oil_i +4.648 \ cdot 10 ^ {-8} \ cdot res_i、$

または、変数をスケーリングする場合：

r u b_{i} = 0.0254 + 0.0042 c d o t o i l_{i} + 0.0031 c d o t r e s_{i} 、

$rub_i = 0.0254 + 0.0042 \ cdot oil_i +0.0031 \ cdot res_i、$

線形回帰について：ルーブル為替レートへのベイズのアプローチ

MNCデータと診断

時系列とエラー

ベイズ回帰と変数の確率的選択

おわりに

ボーナス

More articles: