🐩 👩🏾‍🎓 🐉 FSEエンコーディング 😩 🕧 💢

有限状態エントロピー （FSE）は、ハフマンアルゴリズムと算術コーディングの両方にやや似たエントロピーコーディングアルゴリズムです。同時に、彼は両方からベストを取りました。それはハフマンのものと同じくらい速く動作し、算術符号化のような圧縮率で動作します。

FSEは、 Yarek Dudaによって発明されたANSファミリのコーデック（ Asymmetric Numeral Systems ）に属します。 Jan Colleは、彼の研究に基づいて、後にFSEと呼ばれるアルゴリズムの最適化バージョンを開発しました。

Jan Kolleのメモを理解するのは簡単ではないので、私の意見では、説明を理解しやすいように、少し異なる順序で説明します。

既存のアルゴリズムとの比較

ハフマンアルゴリズムの仕組みを思い出してください。

次の割合の文字で構成されるメッセージがあるとします。

A ：50％; B ：25％; C ：12.5％; D ：12.5％

このような適切な分布を使用すると、次のように文字をエンコードできます。

Aには1ビット、Bには2ビットが必要です。 CおよびD-それぞれ3ビット。

確率分布があまり適切でない場合、たとえば：

A：40％; B：30％; C：15％; D：15％、ハフマンアルゴリズムによれば、まったく同じ文字コードを取得できますが、圧縮はそれほど良くありません。

メッセージの圧縮率は、次の式で表されます。

s u m p_{i} b_{i}

$\ sum p_ib_i$ ここで、 p _i

はメッセージ内で文字が出現する頻度、 b _i

はこの文字をエンコードするビット数です。

エントロピーコーデックの場合、最適な圧縮品質はシャノンの式で表されることが知られています。

- s u m p_{i} l o g_{2} （ p_{i} ）

$-\ sum p_i log_2（p_i）$ 。これを前の式と比較すると、 b _i

は等しくなければならないことがわかります

- l o g_{2} （ p_{i} ）

$-log_2（p_i）$ 。多くの場合、この対数の値は非整数です。

非整数のビット数-それについてどうすればよいですか？

ハフマンアルゴリズムでは、ビット数は最も近い整数に丸められ、圧縮率に悪影響を及ぼします。

算術符号化アルゴリズムは異なるアプローチを使用します。これにより、丸めを行わずに「理想的な」圧縮に近づくことができます。ただし、動作は比較的遅くなります。

FSEアルゴリズムは、前の2つのアプローチのクロスです。 可変ビット数を使用して文字をエンコードする（場合によってはより多く、場合によってはより少ない）ため、 平均して

- l o g_{2} （ p_{i} ）

$-log_2（p_i）$ 文字ごとのビット。

FSEの仕組み

例を考えてみましょう。エンコードされたメッセージで次の割合で文字が出現するようにします。

A ：5; B ：5; C ：3; D ：3

これらの数値を正規化周波数と呼び、 q _i

を示します。

N = s u m q_{i}

$N = \ sum q_i$ -（正規化された）シンボル周波数の合計。

この例では、N = 16です。アルゴリズムが高速に機能するには、Nが2のべき乗であることが必要です。シンボル周波数の合計が2のべき乗と等しくない場合（ほぼ常に）、周波数を正規化する必要があります-2のべき乗が結合されるように、それらを比例的に減少（または増加）する必要があります。これについての詳細は後述します。

N個の列の表を取り、そこにメッセージ文字を記述して、各文字がその頻度とまったく同じ回数発生するようにします。順序はまだ重要ではありません。

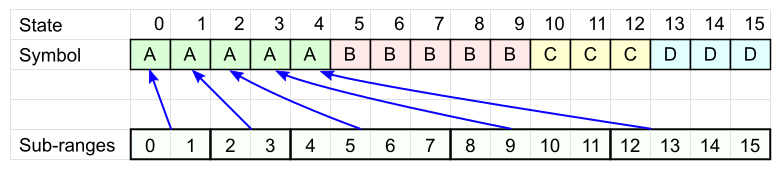
各シンボルAには独自のセル範囲があります（図のサブ範囲 ）：各範囲のサイズは2のべき乗（速度用）で、合計でN個のセルすべてをカバーする必要があります（これまでのところ、これらの範囲の配置は気にしません）。

同様に、残りの各文字について、独自の範囲セットを定義します。

シンボルDには、3つの範囲があります。

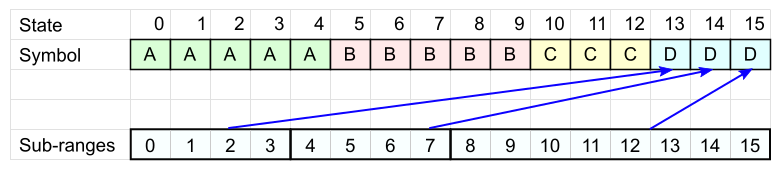
コードテーブルの準備ができました。これを使用して、単語「BCDA」をエンコードします。

最初の文字は「 B 」です。この記号が付いたテーブルセルを選択します。セル番号は現在の状態です。

現在の状態= 5 。
次の文字「 C 」を取ります。 Cのコードテーブルを見て、現在の状態がどの間隔に落ちたかを確認します。

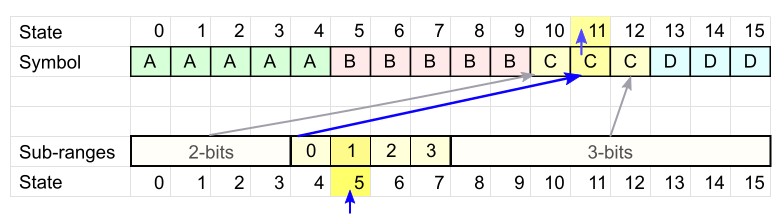
私たちの場合、状態5は2番目の間隔になりました。

この間隔の先頭からオフセットを書き込みます。この例では1です。オフセットを記録するには、 2ビットが必要です。これは、状態が落ちた範囲のサイズです。

現在の範囲は、セル11のシンボルCに対応します。これは、新しい状態= 11を意味します。
後続の文字ごとに手順2を繰り返します。目的のテーブルを選択し、範囲を決定し、オフセットを書き込み、新しい状態を取得します。

各文字について、間隔のオフセットのみが記録されます。このために、異なるビット数が使用されます-「大」または「小」の間隔に入るかどうかによって。平均して、文字あたりのビット数は値になる傾向があります $-log_2（q_i / N）$ 。この事実を証明するには複雑な理論が必要なので、信じてください。
最後の文字がエンコードされると、最終状態になります。保存する必要があり、そこからデコードが開始されます。

デコードは、最後にエンコードされた文字から最初の文字まで、逆の順序で実行されます。

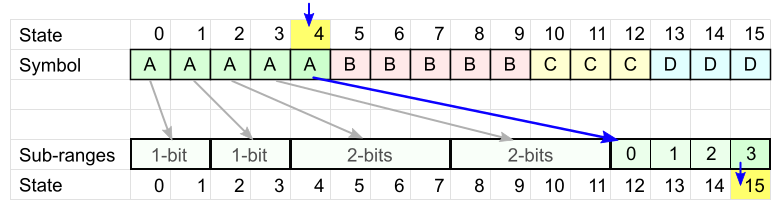
最終状態（4）があり、最後にエンコードされた文字（A）を一意に識別します。
各状態は、コード表の間隔に対応しています。間隔のサイズ（2ビット）に従って必要なビット数を読み取り、次の文字を決定する新しい状態（15）を取得します。
すべての文字をデコードするまで手順2を繰り返します。

エンコードされたデータが終了するか、特別な停止記号が検出されると、デコードが終了します（アルファベットの追加文字が必要です）。

テーブル内のキャラクターの分布

理論では、同じ文字がテーブル全体に均等に分散されていると、コーディングが改善されることがわかります。

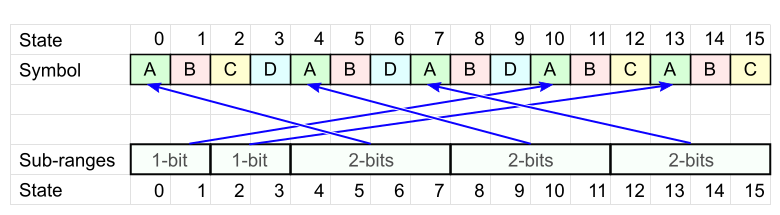
これは、状態が大きな間隔で「停滞」して余分なビットが失われないようにするために必要です。

常に小さな間隔（テーブルの左側）に入るのが良いと思われるかもしれません。しかし、この場合、他のキャラクターはしばしば大きな間隔に落ちます-最終的には悪化するだけです。

最適化

最後に、理論からコードに移りましょう。まず、エンコード中に現在の状態がどの間隔に入るか、何ビット書き込む必要があるかを計算する方法を考えます。

コーディングのために、サイズN（2の累乗に等しい）のテーブルをq _i

間隔に分割する必要があります。これらの間隔のサイズも2のべき乗になります：2 ^ maxbitと2 ^（maxbit-1）-それらを「大」と「小」と呼びましょう。下の図のように、小さな間隔を左側に、大きな間隔を右側にします。

たとえば、N = 16で6つの間隔が必要な場合、パーティションは2 + 2 + 2 + 2 + 4 + 4-サイズ2 ^1の 4つの「小さい」間隔と2 2の2つの「大きい」サイズになります。

大きな間隔のサイズを単純に計算するのは、2のべき乗の最小値です。

2^maxbit >= N / q

したがって、 maxbit = log ₂ (N) - highbit(q)

、ここでhighbit

は最highbit

非highbit

の数です。

q

間隔に戻りましょう。最初に、テーブルを「大きな」間隔に分割します：（N / 2 ^ maxbit）個、次にそれらのいくつかを半分に分割します。間隔を分割すると、合計数が1増えるため、「分割」にはq-（N / 2 ^ maxbit）の大きな間隔が必要になります。したがって、小さな間隔の数は（q-（N / 2 ^ maxbit））* 2になります。

ここで、状態stateがどの間隔で大きな間隔に入るかがわかります。

小さい間隔と大きい間隔の境界を決定するには、小さい間隔の数にサイズを掛けます。

(q - (N / 2^maxbit))*2 * 2^(maxbit-1) = (q * 2^maxbit) - N;

そのstate

は、 state

が大きな間隔に陥ることがわかりました

N + state >= q * 2^maxbit,

それ以外の場合N + state >= q * 2^maxbit,

落ちた間隔のサイズによって、現在の状態からエンコード中に記録する必要がある下位ビット数が決まります。上記の条件が満たされている場合、 nbBitsOut

= maxbit

、それ以外の場合（ maxbit

-1）。残りのステータスビットはスロット番号を決定します。

比較操作の代わりに、十分に大きな数の差分シフトを伴うハックを適用します。

nbBitsOut = ((maxbit << 16) +

N + state - (count << maxbit)

) >> 16;

この式に条件がないため、プロセッサは内部並列処理をより効果的に使用できます。（変数countは、前の式のq記号に対応しています。）

その結果、エンコード関数は次の形式を取ります。

 //      nbBitsOut = ((maxBitsOut << 16) + N + state - (count << maxBitsOut)) >> 16; //  nbBitsOut    state  bitStream: bitStream.WriteBits(state, nbBitsOut); interval_number = (N + state) >> nbBitsOut; //  : state = nextStateTable[deltaFindState[symbol] + interval_number];

事前に計算できるすべてのものを、表に示します。

 symbolTT[symbol].deltaNbBits = (maxBitsOut << 16) - (count << maxBitsOut);

state

は常にN

+ state

として使用されることに注意してください。 N

+ nextStateTable

もnext_state

に格納されている場合、関数は次の形式を取ります。

 nbBitsOut = (N_plus_state + symbolTT[symbol].deltaNbBits) >> 16; bitStream.WriteBits(N_plus_state, nbBitsOut); //  : N_plus_state = nextStateTable[symbolTT[symbol].deltaFindState + (N_plus_state >> nbBitsOut)];

ご覧のとおり、計算は非常に簡単で高速です。

それに応じて、 デコードは次のようになります。

  //    outputSymbol(decodeTable[state].symbol); //   ,     nbBits = decodeTable[state].nbBits; //       offset = readBits(bitStream, nbBits); //   :   +  state = decodeTable[state].subrange_pos + offset;

さらに簡単に！

実際のコードはここにあります。そこでsymbolTT decodeTable.

テーブルsymbolTT decodeTable.

テーブルsymbolTT decodeTable.

どのようにsymbolTT decodeTable.

かを見つけることができますsymbolTT decodeTable.

シンボル周波数の正規化について

上記では、シンボルq _i

周波数の合計が2の累乗に等しいという仮定から進めました。もちろん一般的なケースでは、そうではありません。次に、これらの数値を比例して減らして、合計で2の累乗になるようにする必要があります。

シンボル周波数の合計はコードテーブルのサイズに等しいことに注意してください。テーブルが大きいほど、シンボル周波数がより正確に表示され、圧縮率が向上します。一方、テーブル自体も多くのスペースを占有します。圧縮データのサイズを推定するには、シャノンの式を使用できます

- s u m q_{i} l o g_{2} （ q_{i} / N ）

$-\ sum q_i log_2（q_i / N）$ 、圧縮が理想的であると大胆に仮定し、このようにして最適なテーブルを選択します。

周波数を正規化するプロセスでは、多くの小さな問題が発生する可能性があります。たとえば、一部の文字の確率が非常に小さい場合、表現可能な最小の頻度1 / Nは不正確な近似であることが判明しますが、それは決して少なくなります。この場合の1つのアプローチは、そのような文字にすぐにq _i

= 1を割り当て、コードテーブルの最後に配置して（これが最適です）、残りの文字を処理することです。値を最も近い整数に丸めることも最適なオプションではない場合があります。これと他の多くのニュアンスは、Jan Colle（ 1、2、3、4 ）によってよく書かれています。

高速のヒューリスティックな周波数正規化アルゴリズムと、低速ですがより正確なアルゴリズムの両方があります。選択はあなた次第です。

データモデルの選択

-65536から+65535など、潜在的に大きな範囲の数値をエンコードする必要がある状況を見てみましょう。さらに、これらの数値の確率分布は非常に不均一です。中央に大きなピークがあり、図のようにエッジに非常に小さな確率があります。各値を個別の文字でエンコードすると、テーブルは想像できないサイズになります。

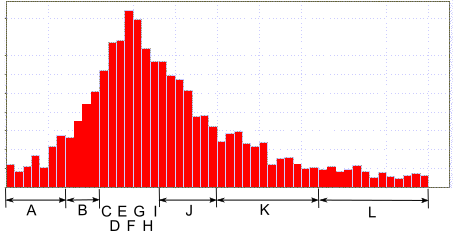
このような状況では、値の全範囲を1文字で示すことができます。 FSEでは、文字自体のみをエンコードし、範囲のサイズに応じて、範囲内のオフセットが「そのまま」書き込まれます。

この手法により、コードテーブルを多少コンパクトにすることができます。

この例は、アルファベットの選択がデータに大きく依存することを示しています。コーディングを最適化するには、少し想像力を働かせる必要があります。

混合コーディング

データの異なる部分に異なる頻度分布がある場合、異なるテーブルを使用してそれらをエンコードすることをお勧めします。

同時に、異なるテーブルを使用して異種データを順番にエンコードできます！ 1つのテーブルの状態は、次の文字を別のテーブルでエンコードするために使用されます。主なことは、デコード時に同じ順序を繰り返すことができるということです。テーブルも同じサイズである必要があります。

たとえば、データを「 チーム-番号-チーム-番号... 」という形式のシーケンスとします。コマンドの後に数字が来ることが常にわかっているため、テーブルが使用される順序が決まります。

データをendから beginにエンコードする場合、デコードするとき（最初から最後まで）、何が続くか、したがって、次の要素のデコードに使用するテーブルが明確になります。

テーブルエントリについて

前述のように、コード表をデコードするには、データとともに保存する必要があります。この場合、テーブルが多くのスペースを占有しないことが望ましいです。

dTableテーブルのフィールドを見てみましょう。

 unsigned char symbol; //     256  unsigned short subrange_pos; //    unsigned char nbBits; //

合計：1文字あたり4バイト。たくさん。

ただし、dTableテーブルの代わりに考えると、正規化されたシンボル周波数のみを保存できます。たとえば、コードテーブルのサイズが2 ⁸ = 256の場合、1文字あたり8ビットで十分です。

周波数がわかれば、エンコーディングとまったく同じdTableを構築できます。

同時に、アルゴリズムがフロートを使用しないことを確認することをお勧めします（異なるプロセッサでは違いがあるため、固定小数点を使用することをお勧めします）。

ところで、これらのテーブルは何らかの形で圧縮することもできます。 ;）

エピローグ

Playrixでは、FSEを使用してベクターアニメーションをエンコードします。フレーム間のデルタは、ゼロに近い分布ピークを持つ多くの小さな値で構成されます。ハフマンからFSEへの移行により、アニメーションのサイズを約1.5倍削減できました。圧縮データはメモリに保存され、解凍は「オンザフライ」で行われ、同時に再生されます。 FSEでは、これを非常に効率的に行うことができます。

参照資料

FSEの仕組みを理解したので、Jan Kolleのブログで詳細を読んで理解を深めることをお勧めします。

GitHubコード（Jan Colleによる）： https : //github.com/Cyan4973/FiniteStateEntropy

FSEエンコーディング